Abstract
Cooper pairs in the superconductor are a natural source of spin entanglement. The existing proposals of the Cooper pair splitter can only realize a low efficiency of entanglement production and its size is constrained by the superconducting coherence length. Here we show that a long-range Cooper pair splitter can be implemented in a normal metal-superconductor-normal metal (NSN) junction by driving a supercurrent in the S. The supercurrent results in a band gap modification of the S, which significantly enhances the crossed Andreev reflection (CAR) of the NSN junction and simultaneously quenches its elastic cotunneling. Therefore, a high entanglement production rate close to its saturation value can be achieved by the inverse CAR. Interestingly, in addition to the conventional entangled electron states between opposite energy levels, novel entangled states with equal energy can also be induced in our proposal.
Similar content being viewed by others
Introduction
Generation and detection of the electron entanglement in solid state physics have attracted great scientific interest, for the prospect of large-scale implementation of quantum information and computation schemes1. The conventional BCS superconductor are considered as a natural source of spin entanglement2,3, for the Cooper pair in the superconductor can break up into two nonlocal entangled electrons that enter into different normal terminals via the crossed Andreev reflection (CAR)4,5. Recently, the feasibility of a Cooper pair splitter has been demonstrated by the nonlocal conductance6,7 and noise8,9 measurement. The finite bias Cooper pair splitting10 and high purity of nonlocal transport by CAR11 were also reported in the quantum dots based splitter. However, the main limitation of the existing proposals is that the entanglement production rate is still at low level, even when the competitive elastic cotunneling (EC) process is filtered out2,5,12,13,14,15,16,17,18,19,20,21. In order to manipulate and probe entangled states22,23,24,25,26,27,28,29,30,31,32,33,34,35, the entanglement production rate demands well improvement. Another constraint on a conventional Cooper pair splitter is that the superconductor size L, the distance between two normal metal-superconductor (NS) interfaces, cannot strongly exceed the superconducting coherence length ξ0 = ħvF/Δ36. A solution of such a geometric constraint will greatly facilitate the fabrication of the splitter.
In this paper, we show that both the problems can be solved with the use of a three-terminal NSN junction by driving a supercurrent in the S along the junction, as sketched in Fig. 1(a). The supercurrent results in opposite shifts of energy gaps for the electron-like and hole-like quasiparticles, as shown in Fig. 1(b). When an electron is incident to the S within the energy window (referred as the CAR window) between the two modified gaps, the hole-like quasiparticle is able to propagate freely in the S, supporting a long-range CAR, while the electron-like quasiparticle decays as usual, leading to a suppression of EC. Therefore, the probability of CAR gets significantly enhanced within the CAR window and oscillates with L. By investigating the entangled states via the inverse CAR process non-perturbatively, we find that there exist two types of spin singlet states, with the entangled electron pair possessing either opposite or equal energies relative to the chemical potential of the S. The total entanglement production rate depends solely on the CAR probability and a high rate close to its saturation value can be achieved.
(a) Illustration of the NSN junction fabricated on a nanowire. A supercurrent Is sketched by the long pink arrow is driven in the S. Two electrons (yellow balls with their spins labeled by the red arrows) from different N regions enter into S and form a Cooper pair during the CAR process. Two gates Vg1,2 (the golden bars) are located at the interfaces. (b) The quasiparticle picture of CAR, with the filled (open) circles representing the electron-like (hole-like) quasiparticles. The supercurrent opens a CAR window sketched by the blank region. The free wave of the hole-like quasiparticle and the evanescent wave of the electron-like quasiparticle are sketched by the inserted boxes.
Long-range CAR
To be specific, we first analyze the CAR in a nanowire NSN junction as shown in Fig. 1(a), where an effective pair potential is induced in the S region due to the proximity effect of the s-wave superconductor. When a supercurrent Is is driven in the S, the effective order parameter in the nanowire takes the form of Δe2iqx 37,38. The Cooper pair momentum 2q can be tuned by the supercurrent through q = is/ξ0, with is = Is/Ic normalized by its critical value Ic. The whole system can be well described by the Bogoliubov-de Gennes Hamiltonian as

where σy is the spin Pauli matrix, µ is the chemical potential and the pair potential is given by Δ(x) = Δe2iqxΘ(x)Θ(L − x) with Θ(x) the Heaviside step function. The Dirac-type interface potentials U(x) = U1δ(x) + U2δ(x− L) are introduced to model the barriers at the NS interfaces39, which can be tuned by gates Vg1,2 as shown in Fig. 1(a).
Hamiltonian (1) in the S region can be diagonalized by assuming the wave function as (uei(k+q)x, vei(k−q)x)T. The excitation energy around ±kF can be obtained as  under the conditions of
under the conditions of  and
and  , with the small wave vectors denoted by
, with the small wave vectors denoted by  . The energy spectra indicate that the excitation gaps around Fermi points ±kF shift by opposite values of ±isΔ, as illustrated in Fig. 1(b). Such energy splitting opens a CAR window, E/Δ ∈ (1 − is, 1 + is), which provides an opportunity to enhance the CAR by filtering out the EC. This can be understood by solving the scattering problem of a spin-up electron incident from the left N lead into the NSN junction. The wave functions in the three regions are given by
. The energy spectra indicate that the excitation gaps around Fermi points ±kF shift by opposite values of ±isΔ, as illustrated in Fig. 1(b). Such energy splitting opens a CAR window, E/Δ ∈ (1 − is, 1 + is), which provides an opportunity to enhance the CAR by filtering out the EC. This can be understood by solving the scattering problem of a spin-up electron incident from the left N lead into the NSN junction. The wave functions in the three regions are given by

where the electron and hole wave components around ±kF are  with
with  and
and  , respectively and
, respectively and  . The scattering amplitudes a1, a2, b1 and b2 denote the AR, CAR, normal reflection and EC, respectively, as shown in Fig. 1(b).
. The scattering amplitudes a1, a2, b1 and b2 denote the AR, CAR, normal reflection and EC, respectively, as shown in Fig. 1(b).
All the scattering amplitudes are solved through the boundary conditions of ΨN = ΨS and ∂xΨS − ∂xΨN = ±2kFZjΨS at two NS interfaces, with the “±” and the index j (= 1, 2) corresponding to the interfaces at x = 0 and L, respectively. The dimensionless barrier strength is defined as Zj = mUj/(ħ2kF). As the right NS interface is transparent (Z2 = 0), the CAR amplitude takes a simple form as

where the auxiliary functions are defined by f(x) = sin(il sin x) and g(x) = sin(il sin x−x) with l = L/ξ0 and the energy dependent phases are defined by φ1,2 = cos−1ω± for ω±≤ 1 and φ1,2 = −i cosh−1ω± for ω±> 1.
As E is within the CAR window, exponential factors β+ and β− in Eq. (2) take imaginary and real values, respectively, corresponding to an evanescent wave of the electron-like quasiparticle in the +kF branch and a free wave of the hole-like quasiparticle in the −kF branch. For Z2 = 0, since there is no branch-crossing scattering at the right interface, propagations of the electron-like and hole-like quasiparticles directly contribute to the EC and CAR processes, respectively. In this case, there exists only the CAR process in the long-range limit  . The numerical results of the CAR probability A2 = |a2|2 as a function of is and E is plotted in Fig. 2(a). One can see that there is a notable region confined by the boundary approximately described by E/Δ = 1 ± is, where the CAR gets effectively enhanced. At the resonant energy levels, the CAR probability can reach a high value of 38%. In Fig. 2(b), we compare the CAR probability A2 and EC probability B2 = |b2|2 in the absence and presence of the supercurrent. For a usual NSN junction of is = 0, both CAR and EC processes are suppressed within the initial gap Δ due to the subgap decay of the normal and anomalous propagators in the S region, while EC dominates the nonlocal transport above the gap. Impressively, when a supercurrent is = 0.5 is driven, the long-range CAR occurs within the CAR window E/Δ ∈ (0.5, 1.5), with the EC being quenched below the modified gap 1.5Δ. This is a new kind of energy filtering effect, which occurs in the S, in contrast to the previous proposal in which the energy filtering is enforced in the normal leads and a large mismatch of Fermi velocities is inevitable14,15.
. The numerical results of the CAR probability A2 = |a2|2 as a function of is and E is plotted in Fig. 2(a). One can see that there is a notable region confined by the boundary approximately described by E/Δ = 1 ± is, where the CAR gets effectively enhanced. At the resonant energy levels, the CAR probability can reach a high value of 38%. In Fig. 2(b), we compare the CAR probability A2 and EC probability B2 = |b2|2 in the absence and presence of the supercurrent. For a usual NSN junction of is = 0, both CAR and EC processes are suppressed within the initial gap Δ due to the subgap decay of the normal and anomalous propagators in the S region, while EC dominates the nonlocal transport above the gap. Impressively, when a supercurrent is = 0.5 is driven, the long-range CAR occurs within the CAR window E/Δ ∈ (0.5, 1.5), with the EC being quenched below the modified gap 1.5Δ. This is a new kind of energy filtering effect, which occurs in the S, in contrast to the previous proposal in which the energy filtering is enforced in the normal leads and a large mismatch of Fermi velocities is inevitable14,15.
Next, we investigate the anomalous dependence of the CAR probability on L of the S region. Within the CAR window, A2 and B2 as functions of L are presented in Fig. 3(a). In the absence of supercurrent, A2 first increases with L and then rapidly decreases, while B2 monotonically decays with L, as known in the usual case. As a supercurrent is driven, while the result of B2 changes little, the situation for A2 is quite different. With increasing L, A2 first increases and then exhibits an oscillatory behavior due to the interference between two NS interfaces. In the large L limit, we have  within the CAR window, so that the CAR amplitude in Eq. (3) reduces to
within the CAR window, so that the CAR amplitude in Eq. (3) reduces to  , which corresponds to an oscillation period of L0 = πξ0/sinh(iφ2). Under the condition of Z2 = 0, the scattering between the ±kF branches at the right NS interface is absent, so that the oscillation period is on a scale of ξ0. The result for finite Z2 is shown in Fig. 3(b). In this case, the branch-crossing scattering can take place at the right NS interface, so that for L ~ ξ0, A2 and B2 exhibit fast oscillations with the period comparable with 1/kF. As L gets larger, the propagation of quasiparticles around +kF branch cannot survive after walking such a long distance. Therefore, the fast oscillation disappears and the interference is contributed again by the free waves around −kF. Due to the branch-crossing scattering at the right NS interface, the hole-like quasiparticle can now be transferred into an electron in the right lead, resulting in a finite EC probability. However, it can be shown that the ratio of the EC probability to the CAR one approximates to
, which corresponds to an oscillation period of L0 = πξ0/sinh(iφ2). Under the condition of Z2 = 0, the scattering between the ±kF branches at the right NS interface is absent, so that the oscillation period is on a scale of ξ0. The result for finite Z2 is shown in Fig. 3(b). In this case, the branch-crossing scattering can take place at the right NS interface, so that for L ~ ξ0, A2 and B2 exhibit fast oscillations with the period comparable with 1/kF. As L gets larger, the propagation of quasiparticles around +kF branch cannot survive after walking such a long distance. Therefore, the fast oscillation disappears and the interference is contributed again by the free waves around −kF. Due to the branch-crossing scattering at the right NS interface, the hole-like quasiparticle can now be transferred into an electron in the right lead, resulting in a finite EC probability. However, it can be shown that the ratio of the EC probability to the CAR one approximates to  for an NSN junction of large L, so that the nonlocal transport is always dominated by the CAR for small Z2. On the other hand, in the tunneling limit of
for an NSN junction of large L, so that the nonlocal transport is always dominated by the CAR for small Z2. On the other hand, in the tunneling limit of  , the two nonlocal processes cancel each other out, consistent with the conventional result36.
, the two nonlocal processes cancel each other out, consistent with the conventional result36.
By applying a negative bias voltage eV ∈ Δ(1 − is, 1 + is) on the left lead while keeping the S and the right lead grounded as shown in Fig. 1(a), the nonlocal differential conductance within the CAR window is equal to  with G0 = e2/h the unit conductance (the positive direction of current is from the right lead into the S). The positive nonlocal conductance manifests a CAR-dominant nonlocal transport. The dependence of Z2 on the gate voltage Vg2 can be calibrated through the normal state transport beforehand, so that the CAR probability can be measured directly by conductance G2.
with G0 = e2/h the unit conductance (the positive direction of current is from the right lead into the S). The positive nonlocal conductance manifests a CAR-dominant nonlocal transport. The dependence of Z2 on the gate voltage Vg2 can be calibrated through the normal state transport beforehand, so that the CAR probability can be measured directly by conductance G2.
Entanglement generation via inverse CAR
By imposing a positive bias voltage (eV < 0) on the left lead and reversing the direction of the supercurrent, the Cooper pair can break up into two nonlocal spin entangled electrons. For the high-efficiency inverse CAR, the entangled state should be analyzed non-perturbatively. We start with the many-body state of incident holes occupying the energy window from the Fermi level to |eV| in the left N region as  , where
, where  generates an incident hole in the left lead with energy E and spin σ (= ↑, ↓) and the vacuum state |0〉 represents the Fermi sea filled up to E = 0 in all NSN regions. The incident and outgoing waves are related to each other via scattering coefficients as27,29
generates an incident hole in the left lead with energy E and spin σ (= ↑, ↓) and the vacuum state |0〉 represents the Fermi sea filled up to E = 0 in all NSN regions. The incident and outgoing waves are related to each other via scattering coefficients as27,29

where  and
and  are the operators of the outgoing hole and electron in lead α( = L, R), respectively, with the energy index omitted and the scattering amplitudes correspond to those in Eq. (2), except that the superscript denote the hole incident case. Substituting Eq. (4) into the expression of |Ψin〉, one arrives at the outgoing state of quasiparticles. Then the entangled state between electrons can be obtained by redefining a new vacuum state
are the operators of the outgoing hole and electron in lead α( = L, R), respectively, with the energy index omitted and the scattering amplitudes correspond to those in Eq. (2), except that the superscript denote the hole incident case. Substituting Eq. (4) into the expression of |Ψin〉, one arrives at the outgoing state of quasiparticles. Then the entangled state between electrons can be obtained by redefining a new vacuum state  , which is related to the original one through
, which is related to the original one through  and by performing a particle-hole transformation as
and by performing a particle-hole transformation as  27,40. The many-body outgoing state can be obtained as
27,40. The many-body outgoing state can be obtained as

where  and
and  are two kinds of nonlocal spin singlet states induced by the inverse CAR with amplitude
are two kinds of nonlocal spin singlet states induced by the inverse CAR with amplitude  and
and  , respectively and
, respectively and  includes the other many-body scattering states, such as the local entangled state and product states (Supplementary information). During the derivation of Eq. (5), we have taken into account the particle-hole symmetry of the scattering matrix and expressed the state with the scattering amplitudes in the electron incident case.
includes the other many-body scattering states, such as the local entangled state and product states (Supplementary information). During the derivation of Eq. (5), we have taken into account the particle-hole symmetry of the scattering matrix and expressed the state with the scattering amplitudes in the electron incident case.
 in Eq. (5) is the usual nonlocal entangled state generated by the CAR, for which the two entangled electrons have opposite energies relative to μ27,40, as shown in the left panel of Fig. 4(a). Since the CAR is an elastic process, the total energy of the two electrons is conserved during the pair breaking. We note that the amplitude κ reduces to
in Eq. (5) is the usual nonlocal entangled state generated by the CAR, for which the two entangled electrons have opposite energies relative to μ27,40, as shown in the left panel of Fig. 4(a). Since the CAR is an elastic process, the total energy of the two electrons is conserved during the pair breaking. We note that the amplitude κ reduces to  in the tunneling limit of
in the tunneling limit of  , consistent with the result in previous literatures27,40.
, consistent with the result in previous literatures27,40.
 is the anomalous entangled state in which the two entangled electrons have the same energy E, as shown in the right panel of Fig. 4(a), which is a natural result obtained in the present non-perterbative approach. From a physical point of view, the coincidence of the AR and CAR processes first results in a double electron occupation at the −E energy level, freezing out the spin freedom therein; then a nonlocal entangled state is induced for the electron pair with equal energy E and opposite spins. Such a nonlocal entangled state has never been discussed before, since in the previous consideration, both a1 and a2 are very small in the tunneling regime and
is the anomalous entangled state in which the two entangled electrons have the same energy E, as shown in the right panel of Fig. 4(a), which is a natural result obtained in the present non-perterbative approach. From a physical point of view, the coincidence of the AR and CAR processes first results in a double electron occupation at the −E energy level, freezing out the spin freedom therein; then a nonlocal entangled state is induced for the electron pair with equal energy E and opposite spins. Such a nonlocal entangled state has never been discussed before, since in the previous consideration, both a1 and a2 are very small in the tunneling regime and  becomes a negligible higher-order contribution27,40. In the present proposal, neither a1 nor a2 is small, so that the state
becomes a negligible higher-order contribution27,40. In the present proposal, neither a1 nor a2 is small, so that the state  becomes observable.
becomes observable.
Given that tunnel attempts in a unit energy interval occur with a frequency 1/h (h is the Plank constant)30,41, the differential production rate of nonlocal entanglement can be calculated by  . By further utilizing the current conservation of the quasiparticles, we obtain
. By further utilizing the current conservation of the quasiparticles, we obtain

in the CAR window for the Cooper pair splitter, which is determined solely by the CAR probability. In the case of Z2 = 0, it is simplified to  , indicating that a saturation value
, indicating that a saturation value  can be achieved at A2 = 0.5. It turns out that the entanglement production rate
can be achieved at A2 = 0.5. It turns out that the entanglement production rate  is not a monotone increasing function of the CAR probability. Only in the tunnel limit,
is not a monotone increasing function of the CAR probability. Only in the tunnel limit,  increases monotonously with A2 because of
increases monotonously with A2 because of  . The numerical result of
. The numerical result of  as a function of the bias voltage eV is shown in Fig. 4(b). When the right NS interface is transparent,
as a function of the bias voltage eV is shown in Fig. 4(b). When the right NS interface is transparent,  can approach its saturation value at the resonant energy levels within the CAR window, indicating that an ideal entangler can be implemented in our proposal. Although finite Z2 may suppress the entanglement production rate, large values of
can approach its saturation value at the resonant energy levels within the CAR window, indicating that an ideal entangler can be implemented in our proposal. Although finite Z2 may suppress the entanglement production rate, large values of  can be obtained even for a stronger barrier Z2 = 1, as shown in Fig. 4(b).
can be obtained even for a stronger barrier Z2 = 1, as shown in Fig. 4(b).
The nonlocal spin entanglement of states  and
and  can be demonstrated through either the violation of the Bell-inequality25,26,27,28,29,30,31,32 or a well-designed spintronic quantum eraser33,34. Both schemes can be achieved by the spin resolved current correlation measurement. In the optimal case of Z2 = 0, the nonlocal spin correlation is purely contributed by
can be demonstrated through either the violation of the Bell-inequality25,26,27,28,29,30,31,32 or a well-designed spintronic quantum eraser33,34. Both schemes can be achieved by the spin resolved current correlation measurement. In the optimal case of Z2 = 0, the nonlocal spin correlation is purely contributed by  and
and  . In the case of Z2 ≠ 0, the signal of entanglement will get weakened since the intervention of EC contributes an opposite current; nevertheless, provided that the CAR dominates the nonlocal transport in the CAR window, the signal of entanglement is always extractable. Moreover, the equal-energy entangled state
. In the case of Z2 ≠ 0, the signal of entanglement will get weakened since the intervention of EC contributes an opposite current; nevertheless, provided that the CAR dominates the nonlocal transport in the CAR window, the signal of entanglement is always extractable. Moreover, the equal-energy entangled state  can also be probed by the bunching behavior in a beam splitter setup35, in consideration of the orbital wave function of the singlet state being symmetric.
can also be probed by the bunching behavior in a beam splitter setup35, in consideration of the orbital wave function of the singlet state being symmetric.
Discussions
Finally, we discuss the experimental realization of our proposal. The long-range Cooper pair splitter in Fig. 1(a) possesses the same configuration as those in the experiments reported in Refs. 6, 7, 9, 11, so that it can be implemented by the existing technology. Since no quantum dot embedded in the nanowire needs to be fabricated, more kinds of nanowires can be adopted to build the NSN junction. A key point is that there needs to be a suppercurrent flowing along the junction, which can be driven by imposing a constant current on the S or by utilizing a magnetic flux in a superconducting loop. Possible renormalization of the Fermi velocity due to the superconducting proximity effect can be compensated by a back gate. In order to realize an entangler with high efficiency and extract pure signal of entanglement, the interface barriers Z1,2 must be carefully tuned by gate voltages Vg1,2. The optimal choice corresponding to the bias voltage configuration in Fig. 1(a) is found to be  and Z2 = 0, which can be realized in the experiment9.
and Z2 = 0, which can be realized in the experiment9.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge University Press, Cambridge, England, 2000).
Recher, P., Sukhorukov, E. V. & Loss, D. Andreev tunneling, Coulomb blockade and resonant transport of nonlocal spin-entangled electrons. Phys. Rev. B 63, 165314 (2001).
Lesovik, G. B., Martin, T. & Blatter, G. Electronic entanglement in the vicinity of a superconductor. Eur. Phys. J. B 24, 287 (2001).
Byers, J. M. & Flatté, M. E. Probing Spatial Correlations with Nanoscale Two-Contact Tunneling. Phys. Rev. Lett. 74, 306 (1995).
Deutscher, G. & Feinberg, D. Coupling superconducting-ferromagnetic point contacts by Andreev reflections. Appl. Phys. Lett. 76, 487 (2000).
Hofstetter, L., Csonka, S., Nygård, J. & Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot Y-junction. Nature (London) 461, 960 (2009).
Herrmann, L. G., Portier, F., Roche, P., Yeyati, A. L., Kontos, T. & Strunk, C. Carbon Nanotubes as Cooper-Pair Beam Splitters. Phys. Rev. Lett. 104, 026801 (2010).
Wei, J. & Chandrasekhar, V. Positive noise cross-correlation in hybrid superconducting and normal-metal three-terminal devices. Nat. Phys. 6, 494 (2010).
Das, A., Ronen, Y., Heiblum, M., Mahalu, D., Kretinin, A. V. & Shtrikman, H. High-efficiency Cooper pair splitting demonstrated by two-particle conductance resonance and positive noise cross-correlation. Nat. Commun. 3, 1165 (2012).
Hofstetter, L., Csonka, S., Baumgartner, A., Fülöp, G., d'Hollosy, S., Nygård, J. & Schönenberger, C. Finite-Bias Cooper Pair Splitting. Phys. Rev. Lett. 107, 136801 (2011).
Schindele, J., Baumgartner, A. & Schönenberger, C. Near-Unity Cooper Pair Splitting Efficiency. Phys. Rev. Lett. 109, 157002 (2012).
Linder, J., Zareyan, M. & Sudbø, A. Spin-switch effect from crossed Andreev reflection in superconducting graphene spin valves. Phys. Rev. B 80, 014513 (2009).
Linder, J. & Yokoyama, T. Superconducting proximity effect in silicene: Spin-valley-polarized Andreev reflection, nonlocal transport and supercurrent. Phys. Rev. B 89, 020504(R) (2014).
Cayssol, J. Crossed Andreev Reflection in a Graphene Bipolar Transistor. Phys. Rev. Lett. 100, 147001 (2008).
Veldhorst, M. & Brinkman, A. Nonlocal Cooper Pair Splitting in a pSn Junction. Phys. Rev. Lett. 105, 107002 (2010).
Chen, W., Shen, R., Sheng, L., Wang, B. G. & Xing, D. Y. Resonant nonlocal Andreev reflection in a narrow quantum spin Hall system. Phys. Rev. B 84, 115420 (2011).
Yeyati, A., Levy, Bergeret, F. S., Martín-Rodero, A. & Klapwijk, T. M. Entangled Andreev pairs and collective excitations in nanoscale superconductors. Nature Phys. 3, 455 (2007).
Golubev, D. S. & Zaikin, A. D. Non-local Andreev reflection under ac bias. Europhys. Lett. 86, 37009 (2009).
Herrera, W. J., Levy Yeyati, A. & Martin-Rodero, A. Long-range crossed Andreev reflections in high-temperature superconductors. Phys. Rev. B 79, 014520 (2009).
Nilsson, J., Akhmerov, A. R. & Beenakker, C. W. J. Splitting of a Cooper Pair by a Pair of Majorana Bound States. Phys. Rev. Lett. 101, 120403 (2008).
Reinthaler, R. W. Recher, P. & Hankiewicz, E. M. Proposal for an All-Electrical Detection of Crossed Andreev Reflection in Topological Insulators. Phys. Rev. Lett. 110, 226802 (2013).
Bell, J. S. On the Einstein Podolsky Rosen Paradox. Physics (Long Island City, N.Y.) 1, 195 (1964).
Bell, J. S. On the Problem of Hidden Variables in Quantum Mechanics. Rev. Mod. Phys. 38, 447 (1966).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed Experiment to Test Local Hidden-Variable Theories. Phys. Rev. Lett. 23, 880 (1969).
Kawabata, S. Test of Bell's Inequality using the Spin Filter Effect in Ferromagnetic Semiconductor Microstructures. J. Phys. Soc. Jpn. 70, 1210 (2001).
Chtchelkatchev, N. M., Blatter, G., Lesovik, G. B. & Martin, T. Bell inequalities and entanglement in solid-state devices. Phys. Rev. B 66, 161320(R) (2002).
Samuelsson, P., Sukhorukov, E. V. & Büttiker, M. Orbital Entanglement and Violation of Bell Inequalities in Mesoscopic Conductors. Phys. Rev. Lett. 91, 157002 (2003).
Samuelsson, P., Sukhorukov, E. V. & Büttiker, M. Two-Particle Aharonov-Bohm Effect and Entanglement in the Electronic Hanbury BrownCTwiss Setup. Phys. Rev. Lett. 92, 026805 (2004).
Beenakker, C. W. J., Emary, C., Kindermann, M. & van Velsen, J. L. Proposal for Production and Detection of Entangled Electron-Hole Pairs in a Degenerate Electron Gas. Phys. Rev. Lett. 91, 147901 (2003).
Beenakker, C. W. J. Electron-hole entanglement in the Fermi sea. arXiv:cond-mat/0508488v3.
Chen, W., Shen, R., Sheng, L., Wang, B. G. & Xing, D. Y. Electron Entanglement Detected by Quantum Spin Hall Systems. Phys. Rev. Lett. 109, 036802 (2012).
Braunecker, B., Burset, P. & Levy Yeyati, A. Entanglement Detection from Conductance Measurements in Carbon Nanotube Cooper Pair Splitters. Phys. Rev. Lett. 111, 136806 (2013).
Chen, W., Shen, R., Wang, Z. D., Sheng, L., Wang, B. G. & Xing, D. Y. Quantitatively probing two-electron entanglement with a spintronic quantum eraser. Phys. Rev. B 87, 155308 (2013).
Chen, W., Wang, Z. D., Shen, R. & Xing, D. Y. Probing spin entanglement by gate-voltage-controlled interference of current correlation in quantum spin Hall insulators. Phys. Lett. A 378, 1893 (2014).
Burkard, G., Loss, D. & Sukhorukov, E. V. Noise of entangled electrons: Bunching and antibunching. Phys. Rev. B 61, R16303 (2000).
Falci, G., Feinberg, D. & Hekking, F. W. J. Correlated tunneling into a superconductor in a multiprobe hybrid structure. Europhys. Lett. 54, 255 (2001).
Romito, A., Alicea, J., Refael, G. & von Oppen, F. Manipulating Majorana fermions using supercurrents. Phys. Rev. B 85, 020502(R) (2012).
Chen, W., Gong, M., Shen, R. & Xing, D. Y. Detecting FuldeCFerrell superconductors by an Andreev interferometer. New J. Phys. 16 083024 (2014).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting micro-constrictions: Excess current, charge imbalance and supercurrent conversion. Phys. Rev. B 25, 4515 (1982).
Prada, E. & Sols, F. Entangled electron current through finite size normal-superconductor tunneling structures. Eur. Phys. J. B 40, 379 (2004).
Levitov, L. S. & Lesovik, G. B. Charge distribution in quantum shot noise. JETP Lett. 58, 230 (1993).
Acknowledgements
We would like to thank A. Baumgartner, M. Heiblum, Jing-Min Hou, Ming Gong, Zheng-Yuan Xue and Tao Zhou for helpful discussions. This work is supported by the State Key Program for Basic Researches of China under Grant No. 2011CB922103 and by the National Natural Science Foundation of China under Grants No. 11174125, No. 91021003 and No. 11374159. Wei Chen is also supported by the Project funded by China Postdoctoral Science Foundation under Grant No. 2014M560419.
Author information
Authors and Affiliations
Contributions
W.C. conceived the project and performed the calculations. W.C. and D.Y.X. wrote the manuscript. All authors discussed the results and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary information for Long-range Cooper pair splitter with high entanglement production rate
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Chen, W., Shi, D. & Xing, D. Long-range Cooper pair splitter with high entanglement production rate. Sci Rep 5, 7607 (2015). https://doi.org/10.1038/srep07607
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep07607
This article is cited by
-
Electron waiting times in hybrid junctions with topological superconductors
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

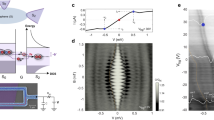




 as a function of bias voltage for different Z2. The relevant parameters are set as L = 8ξ0, Z1 = 1.25, is = −0.5, kF = 100/ξ0.
as a function of bias voltage for different Z2. The relevant parameters are set as L = 8ξ0, Z1 = 1.25, is = −0.5, kF = 100/ξ0.