Introduction

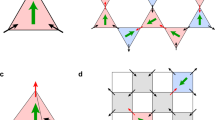
Frustrated spin ices are usually described by Hamiltonians containing only spin-spin interactions. These interactions along with the lattice topology lead to the so called spin ice rules (also named Bernal-Fowler rules). In a 2D kagomé lattice composed of vertices linking 3 spins (figure 1a), the spin ice rule takes the following form: allowed states are either made of 1 incoming and 2 outgoing spins (top raw of figure 1b) or by their equivalents obtained by a time reversal transformation (i.e. 1 outgoing and 2 incoming spins, bottom raw of figure 1b). The spin balance at a vertex i can naturally be represented as a magnetic charge Qi. This entails a simplified spin ice rule: only ±1 charge at each vertex are allowed in the ice state (figure 1b). Therefore, a violation of this rule implies the presence of a +3 or −3 charge (figure 1c).

Figure 1
figure 1

(a) AFM image of CoGd connected nanomagnets in the kagomé geometry. (b) Sketches of the six spin configurations allowed by the ice rule at a vertex. The blue and red spheres of small radius correspond respectively to the -1 and +1 magnetic charges located at the vertex. (c) Sketches of the two forbidden states. The blue and red spheres of large radius correspond to the −3 and +3 magnetic charges. (d) Spin and charge configurations in the Spin Ice II state. (e) A charge crystal in the Spin Ice II state. (f) A spin loop crystal in the ground state. (g) Entropy and charge correlator as a function of temperature in the kagomé DSI framework. The temperature is normalized to the nearest neighbor coupling coefficient.

Full size image

By explicitly including long-range spin-spin interactions, the kagomé dipolar spin ice model (DSI) exhibits a richer behavior than the nearest neighbor interaction version, while it still preserves the ice rule2,3,4. Indeed, the variation of the DSI entropy with respect to the system temperature shows four plateaux each of them being associated to a different phase (figure 1g). At high temperatures, the DSI is in a paramagnetic regime violating the ice rule. When reducing the temperature, the system enters into the spin ice manifold, where the ice rule is unanimously obeyed by all vertices (i.e. composed only of allowed states). However, in this regime spins and magnetic charges are not showing an explicit order. Going to lower temperatures, the system reaches a state named spin ice II. In this recently predicted regime3,4, while spins are still allowed to fluctuate, the magnetic charge distribution is frozen. And, even though magnetic charges do not explicitly appear in the Hamiltonian, a crystal of emerging charges is formed (figure 1d and 1e). Parts of this crystal, made of a succession of positive and negative emerging charges, have been recently experimentally observed by Zhang and col.1. Finally, at low temperatures, the system reaches its ground state which is characterized by a spin-loop crystal in which both the spins and the magnetic charges are ordered (figure 1f).

However, experimentally reaching the spin ice II manifold in artificial systems remains challenging, since the effective temperature has to be controlled and strongly reduced. Different field procedures have been used to explore the energy manifold of artificial spin ice systems (particularly square ice)5,6,7. Concerning the Kagomé lattice, it has been shown that the DSI model has to be considered8 but no spin ice II have been observed8,9. Purely thermal demagnetization was only recently reported1,10,11,12,13, without quantitative comparison to DSI for Kagomé ice.

In this study, we use a Co0.7Gd0.3 ferrimagnetic alloy thin film to form the kagomé lattice. This film has a magnetization of 350 kA/m and a Curie temperature (Tc) of 475 K (see supplementary material A). Heating the film up to 500 K does influence neither its magnetic properties nor its amorphous structure (as checked by X-ray diffraction). This material thus provides the possibility of a thermal demagnetization by cooling the sample from its Curie point without inflicting any damage to the system. The studied arrays are formed of 342 connected nanomagnets, arranged in a kagomé geometry (see figure 1a). The distance between adjacent vertices is 500 nm. At room temperature, due to the shape anisotropy, each element presents a uniform magnetic state, with magnetization oriented along the element's long axis. This mimics a multi-axis Ising spin system.

In a first step, the array is magnetized by the application of an in- plane magnetic field. After reducing the external field to zero, the array is brought above its Curie point and therefore beyond the magnetic order temperature of the alloy. Subsequently, the sample is cooled down. The magnetic configuration of our kagomé structures was experimentally determined by XMCD-PEEM, a direct imaging technique allowing us to image the orientation of the magnetization vector in each nano-magnet. A sample image is presented in figure 2a, along with the corresponding scheme of the spin configuration (figure 2b). After cooling below Tc, every magnet of the network is again uniformly magnetized, but the memory of the saturated state is lost. Analysis of the “spins” and vertices distribution shows that the demagnetization is effective with a remanent magnetization of 3.2% (see supplementary materials C). As the spin ice II state is associated with a charge order, the emerging magnetic charges at each vertex were calculated (figure 2c–e).

Figure 2
figure 2

(a) XMCD-PEEM image, (b) Spin configuration deduced from the XMCD-PEEM image and (c) associated magnetic charge configuration along with domains of emerging magnetic charges (green and yellow) after a thermal demagnetization. (d) Distribution of the measured charge correlator (in red) and calculated distribution in the SI model (black curve). (e) Zoom on the array to show spins, emerging charges and charge domains.

Full size image

Our data indicate that the ice rule is strictly obeyed among more than 3800 observed vertices. Consequently, only ±1 charges are associated to these vertices. In order to get an insight about the charge order, the nearest-neighbor charge correlator <Qi.Qi+1> has been computed for 18 different kagomé networks. As shown in figure 2d, the charge correlator distribution differs clearly from the one expected for the spin ice state8. We found an average value of −0.22 lower than −1/9, the <Qi.Qi+1> value in the spin ice state (c.f.figure 1g). Nevertheless, it remains higher than −1, the value characterizing a fully ordered spin ice II state (perfect crystal of emerging charges). However, quantitative analysis of the spatial charge distribution reveals the presence of a local charge order.

Figure 2c presents ordered charge areas that belong to antiphase charge domains, highlighted in yellow and green. The size of these domains can extend up to 80 vertices i.e. 37% of the total number of vertices in a network. The domains are delimited by domain walls separating vertices of equal charges (figure 2e). These domain walls are analogous to antiphase boundaries. The spin configurations within the charge domains do not exhibit trivial spin order (neither saturated nor crystal loop state).

The domain size distribution extracted from the 18 studied networks is presented in figure 3a. The general trend is a decrease of the number of domains with their size (inset in figure 3a). However, a closer look at the small domain sizes reveals a non-monotonic distribution: domains of 1, 3 and 5 vertices appear to be underrepresented. This sawtooth shape in the domain size distribution is unexpected. We can exclude here any artifact due to our sample as a “classic” rotational field-decaying demagnetization leads to a monotonous domain size distribution very similar to the one expected for the spin ice phase (figure 3b).

Figure 3
figure 3

(a) Distribution of domain sizes (in vertices) after a thermal demagnetization and comparison to the DSI model (error bars represent the fluctuation of the model for the number of samples considered in our experiments). (b) Distribution of domain sizes after a rotating field demagnetization and comparison to the spin ice model. (c) and (d) Numbers of domains per array for domains including 1 to 8 vertices in the DSI framework and in the thermo-kinetic framework respectively.

Full size image

Discussion

To establish the origins of this astonishing domain size distribution, Monte Carlo simulations were employed to study the transition towards the observed partial order of charges admitting thermodynamic equilibrium conditions are met. Figure 3c represents the evolution of the number of domains (with size from 1 to 8 vertices) as a function of the charge correlator (cf. methods). For these domain sizes, the number of domains monotonically decreases with the charge correlator (and temperature) in favor of bigger domains. For charge correlators above −0.55, the number of domains per array monotonically decreases with the size of the domain. Below −0.55, the number of 2 vertices charge domains exceeds the one of size 1 (red/black dot on figure 3c). The number of domains containing three vertices always remains higher than the number of domains having 4 or more vertices. Also note that the occurrence of size 5 and 6 domains (as well as size 7 compared to 8), are quite similar for a nearest neighbor charge correlator <−0.55 (The difference is below 0.1 domain/network). This behavior thus contrasts with our experimental findings. In figure 3a, the experimentally observed domain size distribution is directly compared to the one expected for the DSI model at equilibrium for the same charge correlator. The number of domains with sizes of 1, 3, 5 and 7 is lower compared to the model's predictions whereas the situation is opposite for domains of size 2, 4, 6 and 8. Therefore, at equilibrium the DSI model fails to explain the saw-tooth shape in the size distribution of charge domains obtained using our thermal demagnetization procedure.

As it is often the case with antiphase boundary formation, a kinetic process has to be invoked to explain the observed non-monotonic size distribution. Actually, the demagnetization of the system above its Curie temperature and its subsequent cooling does not necessarily give the system the opportunity to explore the manifold of states and to “thermalize”. On the other hand, it is established that the system does not “remagnetize” homogenously and simultaneously as the final configurations reveal long range interactions. Hence, we modeled the remagnetization process by admitting that “spins” can remagnetize completely and sequentially, while interacting with already magnetized spins. The interactions are due to both short range direct exchange coupling (the elements are connected) and long range dipolar interactions. The probability for a spin to remagnetize in a given state is directly related to its number of already magnetized nearest neighbors and to the energy of the system after the possible magnetization (Maxwell-Boltzmann statistics). In other words, the remagnetization is driven by the dipolar field generated by previously magnetized elements. As represented in figure 3d, the out of equilibrium kinetic process we propose yields a behavior quite different from the previously presented equilibrium model. Even at zero temperature, this finite size system fails to reach the charge crystal phase and the charge correlator is limited to −0.69. The temperature dependence of the number of domains of small sizes also presents some particularities. Although the number of domains of size 1, 5, 7 and 8 tends towards zero for small charge correlators, the number of domains of size 2, 3, 4 and 6 reachs finite values at 0 K and even present a non-monotonic evolution with the charge correlator (and temperature). Finally, for a given charge correlator, the domain size distribution does not decrease regularly, in agreement with our experimental findings. The number of domains of size 1 is equal to the number of domains of size 2 at a charge correlator of −0.32. The same goes for domains of size 3 and 4 at −0.45 and 5 and 6 at −0.37. Therefore, a qualitative agreement with our data is found: The kinetic model reproduces experimental features that cannot be explained by postulating equilibrium conditions. For the sake of clarity, the model was kept basic (i.e. just the essential ingredients are taken into account to reproduced the main physical observations) and we note that the inversion of domain populations occurs at charge correlators lower that the one measured experimentally (−0.22). Our main hypothesis was that the magnetization of each element switches from “0” to “1” and remains stable. It has been recently shown in a system with non-connected elements that the elements magnetization can fluctuate at high temperature in a “superparamagnetic” manner10,12,13. These fluctuations are very efficient in thermalizing the system. Such fluctuations are not observed at the timescale of our observations but it cannot be excluded that they can occur during the cooling down phase. However, the occurrence of such fluctuations is unlikely to give rise to singularities in the domain size distribution as it should drive the system towards equilibrium. Nevertheless, in order to explore the effect of an incomplete thermalization we have run quenched Monte Carlo simulations. A limited number of Monte Carlo steps (1-5-25-50-100) are only performed in order to account for a small number of switching of each element. As presented in supplementary information part D, the evolution of the charge domains size distribution with such a process is qualitatively similar to the equilibrium one. Therefore this model of incomplete thermalization fails to reproduce the specific observed domain size distribution.

In conclusion, we find that the remagnetization process of a connected artificial kagomé spin ice leads to a partial order of emergent magnetic charges. This observation is compatible with the dipolar spin ice model. However a detailed analysis of the charge domain size distribution reveals a particular structure (sawtooth distribution). This distribution cannot be reproduced by Monte Carlo simulations (both at-equilibrium and quenched) and the missing ingredient was found to be the kinetics of the remagnetization process. However, it is remarkable that a simple out-of-equilibrium process reproduces the main features of the equilibrium model. The domain size distribution is shown to be a criterion to discriminate between the different processes. These results bring a new insight into the relaxation processes of thermally excited artificial spin ice.

Methods

The 2D kagomé lattices were fabricated from full films grown by UHV sputtering with a base pressure of 10−9 mbar on Si conducting substrates. Cosputtering of Co and Gd in DC mode was used to adjust the concentration of the alloy to get a Curie temperature of 475 K. The film composition is Si//Ta(5 nm)/Co0.7Gd0.3 (10 nm)/Ru(2.7 nm). Using e-beam lithography and ion beam etching, we have fabricated networks of connected nano-elements with a width of 130 nm. The XMCD-PEEM imaging has been performed at the Nanospectroscopy beam line of the Elettra Synchrotron (Trieste, Italy) at the L3 Co absorption edge.

We performed Monte Carlo simulations for a network of 342 spins that reproduces the size and shape of our experimental networks. Long range dipolar interactions between spins are taken into account and the nearest-neighbor coupling is increased to account for the finite length of the nanomagnets8. The initial temperature was set to T/Jαβ = 100 (where Jαβ is the nearest-neighbor coupling) and corresponds to a high-temperature paramagnetic regime. We employed the standard Metropolis algorithm, but we also included loop-flips to efficiently drive the system into its ground state. A modified Monte Carlo step implies a series of spin and loop flips necessary to achieve decorelation between consecutive sampling configurations. The temperature is then sequentially reduced to lower energy states until the system reaches the ground state manifold. For each temperature value, 10 000 modified Monte Carlo steps are initially performed to ensure a good thermalization, followed by 10 000 modified Monte Carlo steps used for sampling. The nearest-neighbor charge-charge correlator was computed at each step and averaged over the entire ensemble for each temperature value.