Abstract
Strongly correlated phases exhibit collective carrier dynamics that if properly harnessed can enable novel functionalities and applications. In this article, we investigate the phenomenon of electrical oscillations in a prototypical MIT system, vanadium dioxide (VO2). We show that the key to such oscillatory behaviour is the ability to induce and stabilize a non-hysteretic and spontaneously reversible phase transition using a negative feedback mechanism. Further, we investigate the synchronization and coupling dynamics of such VO2 based relaxation oscillators and show, via experiment and simulation, that this coupled oscillator system exhibits rich non-linear dynamics including charge oscillations that are synchronized in both frequency and phase. Our approach of harnessing a non-hysteretic reversible phase transition region is applicable to other correlated systems exhibiting metal-insulator transitions and can be a potential candidate for oscillator based non-Boolean computing.
Similar content being viewed by others
Introduction
Rhythmic activity is ubiquitous in the physical world; and the process of synchronization of coupled oscillatory systems can be observed in the circadian rhythms of organisms1,2,3, the synchronization of an ensemble of fireflies4 and is a distinguishing feature in certain structures of our brain including the neocortex and the thalamus5. Participating elements of a coupled system have the fundamental ability to exhibit a non-linear response to forcing stimuli; and hence under certain conditions, a collectively ordered state emerges from the complex dynamics of such a non-linear system. This motivates the development of physical systems of synchronous oscillators which are energy efficient, compact, scalable and could potentially enable large scale biologically inspired computing algorithms such as associative computing for applications like real-time image and pattern recognition6,7,8,9,10,11,12.
In this paper, we investigate the dynamics of self-sustained electrical oscillations in a prototypical correlated system vanadium oxide (VO2) which undergoes an abrupt first order metal-insulator transition with up to five orders of change in conductivity. Further, we explore the possibility of realizing a coupled system of such VO2 based relaxation oscillators by exploring their synchronization and coupling dynamics. Through experiment and circuit simulation, we demonstrate that a system of capacitively coupled VO2 oscillators exhibits charge oscillations that are synchronized in frequency and phase (anti-lock), thereby allowing the opportunity to harness the non-linear dynamics associated with their synchronization in computational algorithms. Our work enables a unique application and design space for a system of coupled correlated oxide based oscillators particularly suitable for applications in the domain of non-Boolean computing6.
Results
Single Oscillator Dynamics
Electrical oscillations in VO2 harness the first order metal-insulator phase transition, which in this case is triggered electrically. It is well accepted that these oscillations represent a triggering of the insulator-to-metal transition (IMT) followed by a resetting metal-to-insulator transition (MIT) leading to spontaneous oscillations13. However, the physical origin of the electrically driven phase transition and therefore, the fundamental origin of the electrical oscillations in VO2 is widely debated as being electronic14,15,16,17,18,19 or electro-thermally driven20,21. Researchers have also shown evidence of electric field induced nucleation22 as the origin of IMT in VO2, similar to switching in chalcogenide glasses23,24. Some reports elucidate the formation of conducting filaments20,25 that trigger the IMT. This debate is linked to the larger controversy over the fundamental driving physics of the phase transition in VO2, particularly whether it is a Mott14,17,26,27 or a Peierls28,29,30 transition or a weighted contribution from both the mechanisms31. Despite the uncertainty over the unequivocal origin of the electrically driven transition in VO2, our work, as well as other reports in literature32,33, show that the dynamics of such relaxation oscillators can be modulated with temperature, total circuit resistance and capacitance.
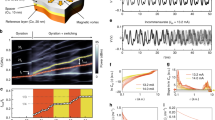
To understand the single oscillator dynamics, we first explore the direct current (DC) characteristics of the oscillator circuit which consists of a two terminal VO2 device (see Methods) with a series resistor Rs (Fig. 1a). The dimensions of the device used for measurements (except in experiments relating to Fig 2b, c) are LVO2 = 4 μm; WVO2 = 10 μm. The device size used in experiments relating to Fig. 1c,d is LVO2 = 4 μm; WVO2 = 80 μm. The series resistor provides a negative feedback and, therefore, modifies the transition dynamics. Unless stated otherwise, all electrical measurements reported are performed near room temperature (18°C).
Stabilizing a non-hysteretic and reversible phase transition in VO2 and single oscillator dynamics.
(a) Schematic of the circuit used to access the non-hysteretic transition regime in VO2 using the negative feedback generated by the series resistor Rs. (b) Rs modifies the VO2 phase transition dynamics through negative feedback. A non-hysteretic reversible (NHR) transition regime can be accessed using the appropriate Rs (>RC). Electrical load lines for non-hysteretic (1) and hysteretic (2) switching are superimposed. (c) Time domain waveform of the VO2 relaxation oscillator. (Inset) shows the waveform for one oscillation period with the two time constants (τ1 = 0.35 μs and τ2 = 0.65 μs) associated with IMT and MIT. (d) Power (Mean Square Amplitude in dB) spectrum of a single oscillator. The fundamental frequency of the oscillator here is ~1 MHz. (e) Simultaneous measurement of the voltage and scattered x-ray diffraction intensity for an oscillating VO2 device. Based upon the Bragg peaks, the structural phase of VO2 is labeled. (Inset) shows the  and [002] Bragg peaks of the M1 and rutile phase of VO2, respectively. The dashed line indicates the θ/2θ angle ( = 51.714°) at which this measurement was performed. Details of x-ray diffraction measurement are described in the Supplementary S4. (f) Frequency scaling of the VO2 relaxation oscillator with Rs. The frequency increases as the external Rs is scaled down. The device resistance has also been scaled to further increase the output frequency.
and [002] Bragg peaks of the M1 and rutile phase of VO2, respectively. The dashed line indicates the θ/2θ angle ( = 51.714°) at which this measurement was performed. Details of x-ray diffraction measurement are described in the Supplementary S4. (f) Frequency scaling of the VO2 relaxation oscillator with Rs. The frequency increases as the external Rs is scaled down. The device resistance has also been scaled to further increase the output frequency.
Injection locking of VO2 oscillators.
(a) Schematic diagram of the injection locking circuit wherein an external AC signal is coupled to the oscillator through a coupling capacitor CC. (b) Power output characteristics of a VO2 relaxation oscillator (Rs = 68 kΩ; ~10Rc) capacitively coupled to an external frequency signal (CC = 1.15 nF) showing locking behavior for frequencies close to its natural oscillation frequency.
When electrically driven across the phase transition with Rs = 0 Ω (Fig. 1b), the IMT and the MIT in VO2 occur at critical fields, E2 and E1, respectively. A current compliance is set to limit the metallic state current and prevent permanent device breakdown. While the exact magnitude of these electric fields depends on the origin of the phase transition (thermal/electronic), they represent a quantitative measure of the stimulus threshold that enables the IMT and the MIT to occur. If the transition is thermally driven then E2 will represent the electric field at which there is enough current density and corresponding thermal flux (most likely to be highly localized) to induce the IMT. Similar consideration applies to electronic case as well as to E1. Therefore, irrespective of the specific physical origin of the transition, the state of VO2 can be described by knowing the electric field across the device. E2 represents the field at which the conducting metallic phase can be stabilized to form a low resistance state while E1 is the field at which the metallic phase can no longer be stabilized and the device returns to its high resistance insulating state. Even though the fundamental mechanism of electric field induced switching remains nontrivial, the delay time22 as a function of DC trigger voltage as well as the temperature dependence of these critical field points is shown in the Supplementary S1. These critical fields differ in magnitude giving rise to a hysteresis in the electrically driven phase transition.
In contrast to this hysteretic transition, a non-hysteretic transition could be induced by modifying the phase transition dynamics such that, triggering the IMT (by surpassing E2) results in a negative differential resistance (NDR) characterized by an increase in conductivity and a simultaneous reduction in the field across the VO2 device. If the electric field across the VO2 now drops below E1, it makes the metallic phase unstable resulting in a spontaneous MIT. Representing this scenario through an electrical load line (Fig. 1b), a VO2 device operating on load line ‘1’ will undergo a non-hysteretic transition, whereas a device operating on load line ‘2’ will go through a hysteretic transition.
While the NDR and the load lines described above cannot be achieved using the RS = 0 Ω configuration, the addition of a simple Rs in series makes this feasible. RS provides a stabilizing negative feedback (see Supplementary S2) compensating the positive feedback associated with the abrupt change in conductivity. This negative feedback modulates the current-electric field characteristics across the VO2 and establishes the load line relation:

where ΔIVO2 = IVO2(EVO2) − IVO2(E2) and LVO2 is the VO2 channel length (see Supplementary S3 for derivation of equation (1) and (2)). From equation (1), it is evident that Rs tunes the VO2 current-electric field characteristics and sets the criteria for non-hysteretic/hysteretic switching. The critical resistance, RC, that enables the non-hysteretic regime of operation, ensures that the metallic phase is never completely stabilized and is given by:

where WVO2and tVO2 are the VO2 channel width and thickness, respectively and σm and σsc are the equivalent insulating and metallic state conductivities, respectively.
The conductivity in the NDR regime as indicated by ΔIVO2 can be tuned by the electric field (equation (1)) with conductivity increasing as the electric field drops (and vice-versa). Such a system can oscillate if the conductivity and electric field across the device modulate each other in a way that the restoring force enables the system to trace the same electrical trajectory periodically34. This criterion is fulfilled only in the non-hysteretic operating regime and hence oscillations are observed only when RS > RC.
The time domain waveform of the VO2 oscillator (Fig. 1c; single time period shown as inset) shows an exponential voltage buildup and decay (across Rs; 5 kΩ in this case) associated with MIT and the IMT in VO2 respectively and is characterized by two R-C time constants τ1 and τ2 (see inset Fig 1c) which primarily control the oscillation frequency. τ1 ( = 0.35 μs), associated with the IMT is smaller than τ2 ( = 0.65 μs). These time constants are much larger than the intrinsic electronic switching time35 of VO2 and therefore oscillation frequency can be scaled by reducing R and C through VO2 device scaling. The corresponding power spectrum for the oscillations is shown in Fig. 1d. The exponential nature of the time domain waveform results in a gradual decay of the frequency harmonics and therefore the first harmonic is approximately 10 dB below the fundamental frequency.
In-situ nano X-ray diffraction (see Supplementary S4) performed on the VO2 film stabilized in an oscillating state (Fig. 1e) confirmed that a structural transition occurs during each oscillation cycle similar to the DC electrically driven phase transition25. The low resistance regime of VO2 during the oscillation cycle is characterized by the rutile metallic phase, whereas the insulating regime is characterized by the monoclinic M1 phase. This is expected for the −0.9% compressively strained VO2 films at room temperature36 (see Methods).
We then study the oscillator frequency (fosc) and dimensional scalability which is crucial to implementing dense, large scale VO2 oscillator circuits. Since fosc is set by the R-C time constant of the oscillator circuit, we explore fosc scaling with RS (Fig. 1f). As Rs is reduced, frequencies up to 1 MHz are experimentally realized. All experiments in this work are performed using discrete components (resistors) and eliminating the parasitic elements associated with the present wiring schemes through monolithic integration along with device scaling will further increase fosc as observed with other correlated materials21,37.
Further, we note that Nardone et al.38 who demonstrated relaxation oscillators in chalcogenide phase change memory, have illustrated some of the stochastic features associated with such oscillations including the observation of multiple oscillatory patterns such as oscillations with decaying amplitudes. We have experimentally observed sustained stable oscillations over 2.5 × 109 cycles (see supplementary S1) with no decaying amplitudes. Additionally, it is expected that the system of coupled VO2 oscillators (described below) will have higher stability to stochastic variations due to mutual feedback induced stabilization39.
Coupled VO2 oscillators and their dynamics
The realization of inductor free and scalable non-linear oscillatory systems using VO2 can be better exploited in the application domain if the oscillators can be synchronously coupled giving access to the large array of non-linear dynamics which are associated with their synchronization. Additionally, long range electrical charge based coupling is crucial to implementing large oscillator arrays compared to other state-variables (like spin), which may have limited coherence length at room temperature.
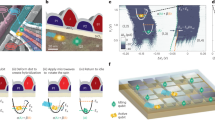
To investigate the coupling dynamics, we first explore ‘injection locking’ wherein a single oscillator is first excited with an external AC sinusoidal signal coupled through a coupling element which in this case is a capacitor CC (Fig. 2a). The oscillator locks onto this external frequency only when it is close to the oscillator's natural frequency and within its lock-in range so that a large power output is observed at the input signal frequency (Fig. 2b). The ability of a single oscillator to lock onto an external AC signal implies that the two coupled oscillators could mutually lock and exhibit synchronized oscillations as investigated further.
Fig. 3a shows a schematic of the coupled oscillator circuit. Prior to coupling, the two individual VO2 oscillators have fosc of 48.43 kHz and 37.27 kHz, respectively (Fig. 3b). fosc is set by choosing appropriate Rs values: 38 kΩ ( = 6Rc) and 47 kΩ ( = 7.5Rc), respectively. After the oscillators are capacitively coupled (CC = 680 pF), they frequency lock and converge to a single resonant frequency (22.95 kHz). This is accompanied by a sharp narrowing of the spectral line width (Fig. 3b). The reduced line-width after locking reflects the mutual feedback induced stabilization against noise39, implying that the synchronized state is a stable configuration for the coupled system.
Synchronized oscillations in VO2 oscillators and their coupling dynamics.
(a) Schematic of two capacitively coupled VO2 oscillators. Individually, the oscillators are tuned to different oscillating frequencies using Rs1 and Rs2 of 38 kΩ ( = 6Rc) and 47 kΩ ( = 7.5Rc), respectively. (b) Experimental and simulated power spectrum of both oscillators before and after coupling. The individual oscillator frequencies lock to a new frequency when coupled capacitively (CC = 680 pF). (c) Effect of CC on the full width at half maximum (FWHM) of the spectral line width and resonant frequency of coupled VO2 oscillators. Decreasing FWHM with increased CC reflects the increased coupling strength. (d) Effect of external resistance symmetry on the coupling strength. The coupling strength is maximal when the oscillators are identical (equal Rs).
The use of capacitive coupling is motivated by the high pass filtering characteristics of the coupling configuration, which ensures that the individual oscillators can synchronize without mutually affecting their DC quiescent point. CC modifies the frequency dynamics of each oscillator through an effective coupling term Ceff

where C1 and C2 are the net capacitances of each oscillator (see macro-model in supplementary). The CC element stores and dynamically redistributes reactive (non-dissipative) power between the oscillators facilitating synchronization. Further, CC also tunes the oscillator coupling dynamics and influences the strength of the coupling interaction between them as indicated by the spectral line-width (full width at half maximum; FWHM) (Fig. 3c). Additionally, Rs, which tunes the natural frequencies of the individual oscillators, also affects the strength of the coupling between the two oscillators. In the symmetric oscillator configuration (equal Rs, identical frequencies for both oscillators), the strongest coupling is observed (Fig. 3d). The ability to tune the synchronization dynamics of the oscillators is crucial from an application standpoint. The experimentally observed frequency locking is also verified through circuit simulations using macro-models (see Supplementary S5), which describe the system's time evolution (Fig. 3b).
The synchronization dynamics of this coupled oscillatory system are analysed using the equivalent model shown in Fig. 4a. The interaction between the two oscillators, each of which traverses between the metallic (M) and the insulating (I) phases, is analysed through the resulting voltage flow diagrams. Figure 4b illustrates the flow diagrams of the coupled systems as they evolve over time. As the VO2 device in each oscillator can be either metallic (M) or insulating (I), the resultant phase plane for the two VO2 devices will consist of four quadrants where the oscillators can be in state MM, MI, IM or II. After coupling, the system will settle on one fixed orbit/trajectory, which may go through these four quadrants. As the device and circuit parameters are changed, the stable orbit will change indicating a different path in the phase plot. The blue arrows indicate a family of such orbits corresponding to the time evolution of the system shown in Fig. 4a. The stable orbit corresponding to our experiment has been shown in red. The stable orbit (red curve in Fig. 4b) of the system has been exclusively shown again in Fig. 4c as a phase plot (V1 vs. V2) along with the corresponding metallic and insulating phases for each VO2 device (the numbers 1,2,3,4 show the related arm in the flow diagrams in Fig. 4b). The phase diagram in Fig. 4c reveals that the synchronized oscillators primarily move between the M-I and I-M planes such that as one VO2 device transitions into the metallic phase, the other device evolves into the insulating phase (b → c; d → a). This is also marked by charging/discharging of the coupling capacitor CC. The region a → b; c → d defines the short phase space trajectory where both the devices have the same phase and represents the time during the coupling capacitor CC reverses polarity. The corresponding time domain waveform of the two oscillators after coupling is shown in Fig. 4d. As the oscillators move in the phase space, the periodic sourcing/draining of charge (Fig. 4d) by the coupling capacitor CC enables the oscillators to synchronize.
Analyzing the coupling dynamics of VO2 oscillators.
(a) Equivalent circuit model for capacitively coupled VO2 oscillators. C1 and C2 are the effective capacitances of each oscillator, which include the internal VO2 capacitance associated with VO2 film and the device (CVO2) as well as parasitic capacitances. Rp → ∞. The same circuit is used to simulate the experimentally observed frequency locking and has been verified with experimental data as shown earlier. (b) Voltage flow diagram in phase space for steady state coupled oscillations. 1–2–3–4 is the electrical trajectory of the capacitively coupled configuration. It reveals that the coupled oscillators primarily move in the M-I and I-M phase planes. (c) The electrical trajectory of the coupled oscillator configuration in phase space. (d) Simulated time domain waveform of the two VO2 oscillators after coupling (top). The to and fro movement of charge (Qc) across the capacitor enables the two oscillators to synchronize (bottom).
Discussion
The non-hysteretic transition dynamics that enable such spontaneous electrical oscillations in VO2 inspires the exploration of other correlated systems for similar applications40,41,42. The coupled oscillatory dynamics demonstrated here provides an important milestone of experimental demonstration of coupled synchronous oscillations in correlated oxide materials and unravels new opportunities towards exploring large coupled oscillatory systems. We anticipate a wide array of dynamics in larger arrays of such coupled oscillators that could potentially be harnessed to develop a robust hardware platform capable of supporting novel computing schemes and algorithms.
Methods
The VO2 two terminal devices are fabricated on a 17.7 nm thick VO2 films. The films are epitaxially grown on a TiO2 (001) substrate employing reactive oxide molecular-beam epitaxy using a Veeco GEN10 system. Due to epitaxial mismatch, the VO2 films are biaxially strained in compression by −0.9%. First the electrodes are patterned using contact lithography followed by electron beam evaporation of Pt/Au (15 nm/80 nm) and lift-off in RemoverPG at 70°C. Next the channel width and isolation are defined by electron beam lithography followed by a CF4 dry etch. Finally, the resist is stripped with RemoverPG at 70°C.
References
Vaz Nunes, M., Lewis, R. D. & Saunders, D. S. A coupled oscillator feedback system as a model for the photoperiodic clock in insects and mites. I. The basic control system as a model for circadian rhythms. J. Theor. Biol. 152, 287–298 (1991).
Kawato, M., Fujita, K., Suzuki, R. & Winfree, A. T. A three-oscillator model of the human circadian system controlling the core temperature rhythm and the sleep-wake cycle. J. Theor. Biol. 98, 369–92 (1982).
Strogatz, S. H. Human sleep and circadian rhythms: a simple model based on two coupled oscillators. J. Math. Biol. 25, 327–47 (1987).
Buck, J. & Buck, E. Mechanism of Rhythmic Synchronous Flashing of Fireflies: Fireflies of Southeast Asia may use anticipatory time-measuring in synchronizing their flashing. Science 159, 1319–1327 (1968).
Steriade, M. Synchronized activities of coupled oscillators in the cerebral cortex and thalamus at different levels of vigilance. Cereb. Cortex 7, 583–604 (1997).
Hoppensteadt, F. & Izhikevich, E. Oscillatory Neurocomputers with Dynamic Connectivity. Phys. Rev. Lett. 82, 2983–2986 (1999).
Vassilieva, E., Pinto, G., de Barros, J. A. & Suppes, P. Learning pattern recognition through quasi-synchronization of phase oscillators. IEEE Trans. Neural Netw. 22, 84–95 (2011).
Shibata, T., Zhang, R., Levitan, S. P., Nikonov, D. E. & Bourianoff, G. I. CMOS supporting circuitries for nano-oscillator-based associative memories. in 2012 13th Int. Work. Cell. Nanoscale Networks their Appl. 1–5 (IEEE, 2012). 10.1109/CNNA.2012.6331464.
Levitan, S. P. et al. Non-Boolean associative architectures based on nano-oscillators. in 2012 13th Int. Work. Cell. Nanoscale Networks their Appl. 1–6 (IEEE, 2012). 10.1109/CNNA.2012.6331473.
Wang, D. & Terman, D. Locally excitatory globally inhibitory oscillator networks. IEEE Trans. Neural Netw. 6, 283–6 (1995).
Hölzel, R. W. & Krischer, K. Pattern recognition with simple oscillating circuits. New J. Phys. 13, 073031 (2011).
Izhikevich, E. M. Weakly pulse-coupled oscillators, FM interactions, synchronization and oscillatory associative memory. IEEE Trans. Neural Netw. 10, 508–26 (1999).
Driscoll, T. et al. Current oscillations in vanadium dioxide: Evidence for electrically triggered percolation avalanches. Phys. Rev. B 86, 094203 (2012).
Kim, H.-T. et al. Mechanism and observation of Mott transition in VO2 -based two- and three-terminal devices. New J. Phys. 6, 52–52 (2004).
Kim, B.-J. et al. Micrometer x-ray diffraction study of VO2 films: Separation between metal-insulator transition and structural phase transition. Phys. Rev. B 77, 235401 (2008).
Sugimoto, N., Onoda, S. & Nagaosa, N. Field-induced metal-insulator transition and switching phenomenon in correlated insulators. Phys. Rev. B 78, 155104 (2008).
Stefanovich, G., Pergament, A. & Stefanovich, D. Electrical switching and Mott transition in VO2 . J. Phys. Condens. Matter 12, 8837–8845 (2000).
Pergament, A. L., Boriskov, P. P., Velichko, A. A. & Kuldin, N. A. Switching effect and the metal–insulator transition in electric field. J. Phys. Chem. Solids 71, 874–879 (2010).
Boriskov, P. P., Pergament, A. L., Velichko, A. A., Stefanovich, G. B. & Kuldin, N. A. Metal-insulator transition in electric field: A viewpoint from the switching effect. 18 (2006). at <http://arxiv.org/abs/cond-mat/0603132>.
Zimmers, A. et al. Role of Thermal Heating on the Voltage Induced Insulator-Metal Transition in VO2 . Phys. Rev. Lett. 110, 056601 (2013).
Gu, Q., Falk, A., Wu, J., Ouyang, L. & Park, H. Current-driven phase oscillation and domain-wall propagation in WxV1-xO2 nanobeams. Nano Lett. 7, 363–6 (2007).
Pevtsov, A. B. et al. Evidence of field-induced nucleation switching in opal: VO2 composites and VO2 films. Phys. Rev. B 85, 024110 (2012).
Karpov, V., Kryukov, Y., Karpov, I. & Mitra, M. Field-induced nucleation in phase change memory. Phys. Rev. B 78, 052201 (2008).
Karpov, V. G., Kryukov, Y. A., Mitra, M. & Karpov, I. V. Crystal nucleation in glasses of phase change memory. J. Appl. Phys. 104, 054507 (2008).
Freeman, E. et al. Nanoscale structural evolution of electrically driven insulator to metal transition in vanadium dioxide. Appl. Phys. Lett. 103, 263109 (2013).
Zylbersztejn, A. Metal-insulator transition in vanadium dioxide. Phys. Rev. B 11, 4383–4395 (1975).
Rice, T. M. & Pouget, J. P. Comment on “VO2: Peierls or Mott-Hubbard? A View from Band Theory.”.Phys. Rev. Lett. 73, 3042–3042 (1994).
Wentzcovitch, R. M. VO2: Peierls or Mott-Hubbard? A view from band theory. Phys. Rev. Lett. 72, 3389–3392 (1994).
Cavalleri, A., Dekorsy, T., Chong, H., Kieffer, J. & Schoenlein, R. Evidence for a structurally-driven insulator-to-metal transition in VO2: A view from the ultrafast timescale. Phys. Rev. B 70, 161102 (2004).
Eyert, V. VO2: A Novel View from Band Theory. Phys. Rev. Lett. 107, 016401 (2011).
Biermann, S., Poteryaev, A., Lichtenstein, A. & Georges, A. Dynamical Singlets and Correlation-Assisted Peierls Transition in VO2 . Phys. Rev. Lett. 94, 026404 (2005).
Kim, H.-T. et al. Electrical oscillations induced by the metal-insulator transition in VO2 . J. Appl. Phys. 107, 023702 (2010).
Sakai, J. High-efficiency voltage oscillation in VO2 planer-type junctions with infinite negative differential resistance. J. Appl. Phys. 103, 103708 (2008).
Hu, C. J. Self-Sustained Oscillation in an R - C or R- L Circuit Containing a Hysteresis Resistor RH . IEEE Trans. Circuits Syst. 33, 636–641 (1986).
Kar, A. et al. Intrinsic electronic switching time in ultrathin epitaxial vanadium dioxide thin film. Appl. Phys. Lett. 102, 072106 (2013).
Park, J. H. et al. Measurement of a solid-state triple point at the metal-insulator transition in VO2 . Nature 500, 431–4 (2013).
Pickett, M. D. & Williams, R. S. Sub-100 fJ and sub-nanosecond thermally driven threshold switching in niobium oxide crosspoint nanodevices. Nanotechnology 23, 215202 (2012).
Nardone, M., Karpov, V. G. & Karpov, I. V. Relaxation oscillations in chalcogenide phase change memory. J. Appl. Phys. 107, 054519 (2010).
Kaka, S. et al. Mutual phase-locking of microwave spin torque nano-oscillators. Nature 437, 389–92 (2005).
Brockman, J. Electric Field-induced Conductivity Switching in Vanadium Sesquioxide Nanostructures. Ph.D thesis, Stanford Univ. (2012).
Asamitsu, A., Tomioka, Y., Kuwahara, H. & Tokura, Y. Current switching of resistive states in magnetoresistive manganites. 388, 1995–1997 (1997).
Scherwitzl, R. et al. Electric-field control of the metal-insulator transition in ultrathin NdNiO3 films. Adv. Mater. 22, 5517–20 (2010).
Acknowledgements
This work was supported by Office of Naval Research through award N00014-11-1-0665. AP was partially funded by a gift from Intel Corporation. G.S. received partial support from the National Science Foundation award DMR-0820404. SD and VN acknowledge funding, in part, from the National Science Foundation Expeditions in Computing Award-1317560. Work at Argonne National Laboratory was supported by the U.S Department of Energy, under Contract No. DE-AC02-06CH1135.
Author information
Authors and Affiliations
Contributions
N.S. performed the experiments and analysed the data. A.P. performed the simulations. E.F. fabricated the devices and H.P. grew the VO2 films. E.F., G.S., H.W. and Z.C. performed the nano X-ray characterization. S.D. conceived and directed the experiment. V.N., V.G., R.E.-H., D.S. and A.R. supervised the study. N.S., S.D., V.G., A.R., R.E.-H. and D.S. wrote the manuscript. All authors discussed the results and commented on the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. The images in this article are included in the article's Creative Commons license, unless indicated otherwise in the image credit; if the image is not included under the Creative Commons license, users will need to obtain permission from the license holder in order to reproduce the image. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Shukla, N., Parihar, A., Freeman, E. et al. Synchronized charge oscillations in correlated electron systems. Sci Rep 4, 4964 (2014). https://doi.org/10.1038/srep04964
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04964
This article is cited by
-
Emerging Memory Technologies for Data Storage and Brain-Inspired Computation: A Global View with Indian Research Insights with a Focus on Resistive Memories
Proceedings of the National Academy of Sciences, India Section A: Physical Sciences (2023)
-
Ising machines as hardware solvers of combinatorial optimization problems
Nature Reviews Physics (2022)
-
A three-terminal non-volatile ferroelectric switch with an insulator–metal transition channel
Scientific Reports (2022)
-
Role of ambient temperature in modulation of behavior of vanadium dioxide volatile memristors and oscillators for neuromorphic applications
Scientific Reports (2022)
-
An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators
Nature Electronics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.