Abstract
To develop a full understanding of interactions in nanomagnet arrays is a persistent challenge, critically impacting their technological acceptance. This paper reports the experimental, numerical and analytical investigation of interactions in arrays of Co nanoellipses using the first-order reversal curve (FORC) technique. A mean-field analysis has revealed the physical mechanisms giving rise to all of the observed features: a shift of the non-interacting FORC-ridge at the low-HC end off the local coercivity HC axis; a stretch of the FORC-ridge at the high-HC end without shifting it off the HC axis; and a formation of a tilted edge connected to the ridge at the low-HC end. Changing from flat to Gaussian coercivity distribution produces a negative feature, bends the ridge and broadens the edge. Finally, nearest neighbor interactions segment the FORC-ridge. These results demonstrate that the FORC approach provides a comprehensive framework to qualitatively and quantitatively decode interactions in nanomagnet arrays.
Similar content being viewed by others
Introduction
Nanomagnet arrays are basic building blocks1 for key technologies such as ultrahigh density magnetic recording media2,3,4, magnetic random access memory (MRAM)5,6 and logic devices7,8,9. Interactions within the arrays critically affect the functionalities of the nanomagnets as well as enable new device concepts. For instance, dipolar interactions may trigger an analog memory effect in nanowire arrays10, enable digital computation in magnetic quantum-dot cellular automata systems7,8,11, lead to frustrations in artificial “spin ice”12,13,14, or adversely affect thermal stability and switching field distribution in magnetic recording media or MRAM elements5,15,16,17. Probing and managing these interactions is often difficult because they are long-ranged, anisotropic and configuration-dependent17.
The first-order reversal curve (FORC) method18,19 has provided detailed characterization for a variety of magnetic20,21,22,23,24,25,26,27 and other hysteretic systems28,29. However, a coherent framework to interpret the features of the FORC diagrams and extract quantitative information is still lacking despite decades of effort by numerous groups. In this work, using the FORC method we have quantitatively investigated tunable interactions in model systems of single domain nanomagnet arrays. With mean-field level simulations, supplemented with a cluster extension, we have reproduced all features and trends of the experimental FORC diagrams quantitatively and identified their physical origins. Our approach decodes interactions in nanomagnet arrays, even disordered arrays and also presents a pathway to evaluate (de)stabilizing interactions in other hysteretic systems.
Results
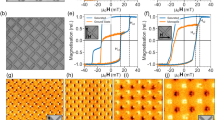
Rectangular arrays of polycrystalline Co ellipses were fabricated with varying center-to-center spacing by magnetron sputtering, in conjunction with e-beam lithography and lift-off. Details are presented in Methods. The ellipses have major/minor axes of 220/110 nm, with a structure of Ta(1 nm)/Co(9 nm)/Ta(1 nm), forming 50 × 50 μm2 arrays. In arrays A1/2/3 the minor-axis spacings of 150/200/250 nm are less than the major-axis spacing of 500 nm. Thus the mean dipolar interactions are demagnetizing, favoring anti-parallel alignment. In arrays B1/2/3 the minor-axis spacing of 500 nm exceeds the major-axis spacings of 250/300/350 nm. Therefore, the mean dipolar interactions are magnetizing, favoring parallel alignment. Scanning electron microscopy (SEM) and magnetic force microscopy (MFM) images, at remanence after DC demagnetization, of arrays A1 and B1 are shown in Figs. 1 and 2, respectively. MFM image contrast indicates the out-of-plane stray fields and confirms the ellipses' single domain state.
FORC measurements were performed to obtain magnetization M(H, HR) under different reversal field HR and applied field H. The FORC-distribution is then extracted18,  , where MS is the saturation magnetization. In loose analogy to the Preisach model, the FORC-distribution in certain simple cases can be interpreted as the 2-dimensional distribution of elemental hysteresis loops with unit magnetization called hysterons on the (H, HR) plane, or on the corresponding (HC, HB) plane, defined by local coercivity HC = (H-HR)/2 and bias/interaction field HB = (H+HR)/2.
, where MS is the saturation magnetization. In loose analogy to the Preisach model, the FORC-distribution in certain simple cases can be interpreted as the 2-dimensional distribution of elemental hysteresis loops with unit magnetization called hysterons on the (H, HR) plane, or on the corresponding (HC, HB) plane, defined by local coercivity HC = (H-HR)/2 and bias/interaction field HB = (H+HR)/2.
Good agreement between measured and simulated FORC-distributions was obtained for all studied arrays [e.g., Figs. 1(c) and (d) for array A2]. All demagnetizing FORCs A1/2/3 exhibited a ridge with the high-HC end on the HC axis and the low-HC end shifted in the +HB direction30. Increasing interactions in A3→A2→A1 increased the low-HC shift and the length of the ridge. In addition, an edge emerged from the low-HC end towards negative HB, highlighted by the arrows, forming a “wishbone” or boomerang structure24. A negative feature is observed at negative HB values near the high-HC end. Similarly, FORC distributions for the magnetizing arrays also exhibit a ridge with the high-HC end on the HC axis, but with the low-HC end shifted towards −HB [e.g., Figs. 2(c) and (d) for array B2]. Increasing interactions again increase the low-HC shift, but reduce the length of the ridge30. A negative feature below the ridge is more prominent than that in the demagnetizing case.
Non-interacting case
A FORC gives a non-zero contribution to ρ(H, HR) only if dM/dH along the FORC depends on HR. We first show that in the non-interacting case ρ coincides with the coercivity distribution D(HK), spread along the HC axis. Indeed, particle Pi with coercivity HKi down-flips at Hdni= −HKi and up-flips at Hupi= HKi. Therefore, on a FORC starting at HR > −HKi, Pi starts out up-flipped and remains so, not contributing to dM/dH nor ρ.
In contrast, on FORC(H, HR= −HKi), Pi is the last to down-flip along the major loop and has the highest coercivity among the down-flipped particles. Therefore, Pi is the last to up-flip as H increases past HKi on the same FORC, causing a dM/dH > 0 jump. Since this dM/dH jump is unmatched by the neighboring FORC(H, HR> −HKi), dM/dH exhibits a dependence on HR, making d(dM/dH)/dHR non-zero. dM/dH increases as HRdecreases, making a positive contribution to ρ at (H = HKi, HR= −HKi).
For all subsequent FORCs at HR < −HKi, Pi starts out down-flipped but still up-flips at H = HKi. The dM/dH jumps on these FORCs are matched since they occur at the samefield on each FORC(H, HR < −HKi). Thus dM/dH is independent of HR and doesn't contribute to ρ. This reasoning highlights that only dM/dH jumps on individual FORCs that are unmatched by neighboring FORCs contribute to ρ. Each particle Pi contributes to ρ only once, at (H = HKi, HR= −HKi) or equivalently at (HC= HKi, HB= 0). The contributions of all particles gives rise to a ridge along the HC (HR= −H) axis, which reflects D(HK).
Interacting case
Next, we introduce interactions between nanomagnets on the mean-field level by including an interaction field Hint= αM(H), where α<0 for demagnetizing systems and α>0 for magnetizing ones21. Fig. 3(a) shows a sequence of FORCs for a demagnetizing system with a rectangular D(HK) and a zoom-in view of the boxed region (right panel). The three FORC segment-pairs (1)/(2)/(3) show that the last dM/dH jump on each FORC(H, HR = −HKi-αM(HR)) - caused by the last up-flipping particle P(HKi) - is unmatched by the neighboring FORC(H, HR > −HKi-αM(HR)).
(a) Schematic illustration of family of FORCs for arrays with a flat coercivity distribution and mean-field demagnetizing interactions, with bold lines and numbers indicating unmatched dM/dH jumps. Calculated FORC distributions are shown in (b) illustrating the construction of the ridge and (c) the edge. (d) FORC distribution with the same interactions, but a Gaussian coercivity distribution; emergent negative feature is indicated by the dashed boundary. Similar panels are shown in (e–h) for the magnetizing case.
Fig. 3(b) shows that with interactions the unmatched dM/dH jumps still generate the ridge, but at shifted HB values. Importantly, on the mean-field level all particles experience the same interaction field and thus the order of flips continues to be governed by the order of the coercivities: along the major loop the particles down-flip in the order of their coercivities, lowest (highest) coercivity particle P(HKmin) first [P(HKmax) last]. Starting at the low-HC end, the lowest coercivity particle P(HKmin) down-flips at Hdnmin= −HKmin-αMS, as no other particles have flipped yet: M(Hdnmin) = MS. Increasing H along FORC(H, HR = Hdnmin), P(HKmin) up-flips at Hupmin= HKmin-αMS, causing a positive jump dM/dH > 0 as shown by the lower FORC(H, HR = Hdnmin)-segment of pair (1). This jump, caused by P(HKmin), is absent on the upper FORC(H, HR> Hdnmin)-segment and is thus unmatched, contributing to ρ at (H = HKmin-αMS, HR= −HKmin-αMS), or similarly at (HC= HKmin, HB= −αMS), defining the low-HC end. These flipping fields are shifted from their non-interacting values, as shown by the arrow set (1) in Fig. 3(b). Since P(HKmin) defines the low-HC end of the FORC-ridge, one concludes that interactions shift the low-HC end of the FORC-ridge to the +HB direction by −αMS (recall α < 0), but leave its HC coordinate un-shifted at HC= HKmin.
FORC-segment pairs (2)/(3) in Fig. 3(a) illustrate the up-flip of higher coercivity particles P(HKi). P(HKi)s create unmatched dM/dH jumps on FORCs where they were the last to down-flip at Hdn = −HKi-αM(HR) [vertical arrows in Fig. 3(b)] and also are the last to up-flip at Hup = HKi-αMS [horizontal arrows in Fig. 3(b)], since M(Hupi) = MS when P(HKi) up-flips.
The high-HC end of the FORC-ridge is defined by P(HKmax) that is the last to down-flip when the rest of the system is already negatively saturated (M = −MS), thus Hdnmax= −HKmax-(−αMS). P(HKmax) up-flips along the FORC(H, HR = Hdnmax) only after the rest of the system is positively saturated: Hupmax= HKmax-αMS. Accordingly, the unmatcheddM/dH jumps caused by P(HKmax) contributes to ρ only at (H = HKmax-αMS, HR= −HKmax+αMS), or similarly at (HC= HKmax-αMS,HB= 0), defining the high-HC end. As observed before, the high-HC end of the FORC-ridge remains on the HC axis24, but stretched along the HC axis by −αMS (α<0).
Note that interactions shift the FORC ridge feature in H uniformly [Fig. 3(b)], i.e., the resultant projection of FORC distribution onto the H-axis is only displaced from its intrinsic values, but not distorted. This H-projection therefore mirrors the non-interacting case, where HUp= HC= H, reflecting the intrinsic coercivity distribution, simply displaced by −αMS. Thus the intrinsic coercivity distribution can be - without distortion from interactions – directly identified from the FORC distribution.
Figs. 1(c,d) and 3(b,c) show that besides the ridge, ρ exhibit an edge as well with interactions27. As discussed earlier, in the absence of interactions, the dM/dH jumps along a FORC(H, HR = −HKi) are matched by the jumps on the subsequent FORC(H, HR < −HKi)s, not contributing to ρ. The arrows of Fig. 3(a) show that the interactions destroy this matching specifically at the low-HCend by shifting the first up-flip field Hupmin of each FORC, caused by P(HKmin), by −αM(HR). These shifts make the dM/dH jumps misaligned, see FORC-segment-pairs (4) and (5) (above and below), thus contributing to ρ at (H = HKmin-αM(HR), HR). These unmatched jumps give rise to the edge in Fig. 3(c). The end-points of the edge are (H = HKmin-αMS, HR= −HKmin-αMS) and (H = HKmin+αMS, HR= −HKmax+αMS), or alternatively (HC= HKmin, HB= −αMS) and (HC= (HKmin+HKmax)/2, HB= αMS+(HKmin-HKmax)/2). Accordingly, the tilt and asymmetry of the edge provide a direct measure of the width of coercivity distribution D(HK) = HKmax-HKmin. In the extreme case of nearly identical nanomagnets with D(HK) = HKmax-HKmin≈0, the edge is vertical in the HC–HB plane, at HC= HK and HB within ± αMS, as observed experimentally in Ni nanowire arrays10.
In short, on the mean-field level the FORC-distribution of a system with demagnetizing interactions exhibits an edge and a ridge, shifted by the unmatched first and last dM/dH jumps along each FORC. The FORC-distribution vanishes between them for the considered flat coercivity distribution, because jumps between the first and the last jumps along each FORC are matched by jumps on the neighboring FORCs. Here, the matched jumps are not caused by the same particles, as in the non-interacting system, but rather by different particles whose up-flipping fields were shifted into alignment by the interactions. Still, the jumps are matched because the values of the aligned jumps are the same on neighboring FORCs for a flat distribution D(HK). Visibly, the flat coercivity distribution on the mean-field already reproduces most features of the measured FORC-distribution.
To improve our model we introduce a more realistic Gaussian D(HK) to elucidate the origin of the negative features, which represent a clear distinction between FORC and a literal Preisach interpretation. A Gaussian breaks the matching of jumps as now shown by examining the set of particles {P(HKCent)} around the center of the coercivity distribution. A P(HKCent) particle is the last to down-flip at HR= −HKCent, where M(HR) = 0 and the last to up-flip on the FORC(H, HR= −HKCent), contributing to ρ at (H = HKCent-αMS, HR= −HKCent). On FORC(H, HR< −HKCent)s P(HKCent) is no longer the last to up-flip. On subsequent FORCs, up-flip jumps from different particles get shifted into alignment with this jump. For the flat distribution, the number of particles shifted into alignment is steady, making the match complete and thus zero contribution to ρ. However, for the Gaussian distribution, the particles shifted into alignment come from the decreasing slope of the Gaussian, leading to dM/dH jumps with a decreasing magnitude, providing only a partial-match and generating a negative contribution to ρ. Fig. 3(d) shows the FORC-distribution for a Gaussian model that indeed develops a negative region specifically tracking the decreasing slope of the Gaussian, highlighted by the dashed line. Analogous arguments show that a Gaussian D(HK) also bends the ridge and broadens the edge.
Nearest-neighbor correlations
The last unaccounted feature of the measured ρ is the segmenting of the FORC-ridge into separate low-HC and high-HC ends, with different amplitudes. To explain this we include the nearest-neighbor interaction fields Hnni(conf) as the first terms of a systematic cluster-expansion.
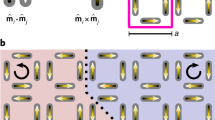
Decreasing the field from positive saturation, the weakest coercivity particles down-flip first. For demagnetizing interactions, Hnni(conf) of these down-flipped particles stabilize their nearest-neighbors in their up state. Therefore, for a sufficiently narrow D(HK), the magnetization decreases towards zero by developing a checkerboard pattern [Fig. 1(b)]. The checkerboard naturally forms defects where the sequence of increasing coercivities selects third-nearest neighbor particles to down-flip. Still, the dominant reversal mechanism for nearly half of the particles is the checkerboard formation: down-flipping with all-up neighbors. Accordingly, the (nearly) half of the FORC ridge with HKi< HKCent gets shifted along the +HB axis by Hnni(up), where Hnni(up) is the interaction field for the all-neighbors-up configuration. Once the checkerboard pattern is formed, the rest of the particles flip with neighbors in various intermediate configurations. Therefore, the HKi> HKCent half of the ridge is broken into several pieces, shifted by varying Hnni(conf) fields. Consequently, the nearest neighbor interactions manifest as segmenting of the ridge30.
To reiterate, the demagnetizing interactions (α < 0) (1) shift the non-interacting FORC-ridge at the low-HC end to the +HB direction by −αMS; (2) stretch the non-interacting FORC-ridge at the high-HC end along HC by −αMS without shifting it off the HC axis; and (3) form a tilted edge connected to the ridge at the low-HC end. Changing from flat to Gaussian D(HK) distribution (4) produces a negative feature, bends the ridge and broadens the edge. Finally, (5) nearest neighbor interactions segment the FORC-ridge.
Magnetizing interactions
Adapting the above arguments for magnetizing interactions (α > 0): (1) the low-HC end is shifted in the −HB direction and (2) the high-HC end is compressed without shifting it off the HC axis [Fig. 3(f)]. (3) Regarding the edge, the first up-flip along each branch is shifted by interactions in the opposite direction as the demagnetizing case [Fig. 3(e) right panel]. Therefore, the first dM/dH jumps are unmatched, decreasing in magnitude with more negative HR, thus negatively incrementing the FORC, forming a negative edge [Fig. 3(g)]. Changing from flat to Gaussian D(HK) distribution (4) the negative edge gets pressed towards the positive ridge and the FORC-ridge becomes curved [Fig. 3(h)]. The inclusion of nearest neighbor terms leads to (5) an avalanche reversal, collapsing the FORC-ridge to a single-value31.
Quantifying Interaction Fields
Finally, we demonstrate the quantitative predicting power of the above considerations. The lowest HKi, which is shifted in HB by αMS, is extracted from the FORC ridge by selecting an HC(threshold) such that 10% of the particles have HKi< HC(threshold) and averaging ρ over the HC= 0→HC(threshold) range. The averaged (dM/dHB)' are shown in insets of Figs. 4(a) and 4(b). The HB shift is determined by linearly extrapolating (dM/dHB)' at the high |HB| end to zero. The interaction field is calculated by a finite element method (using the NIST OOMMF code) for the nearest and next nearest neighbors and treating the remainder of the array as point dipoles. The experimental HB shifts and the calculated interaction fields agree remarkably well (Fig. 4), confirming the validity of the mean-field description of the FORC-distribution and its quantitative predictive power, making the FORC technique a tool to extract numerical values of interaction fields. This is particularly important for disordered arrays where calculations of interactions are not easily achievable.
Calculated (open symbols) and experimentally determined (solid symbols) interaction field for (a) demagnetizing arrays A1/2/3 and (b) magnetizing arrays B1/2/3.
Averaged FORC-distribution utilizing the HC(threshold) are shown in insets for the (a) A2 and (b) B2 array, where the linear extrapolation is illustrated by the dashed line and open circle.
Discussion
In this work, systems of interacting nanomagnets were examined experimentally, numerically and analytically, using the FORC technique. A mean-field analysis based on the concept of unmatched jumps accounted for all experimentally observed features of the FORC diagram, including its shifted ridge-and-edge structure and negative features. The tilting, shifting and stretching of these structures were identified as tools to extract quantitative information about the system, demonstrating the predictive power of the FORC technique. Construction of the FORC distribution through unmatched jumps and recognizing the (de)magnetizing interactions as a particular case of (de)stabilizing interactions, presents an approach which can be used to evaluate any hysteretic system with the FORC technique.
Methods
Arrays of Co ellipses were fabricated by DC magnetron sputtering, in a vacuum chamber with a base pressure of 1 × 10−8 Torr and Ar sputtering pressure of 2 × 10−3 Torr, on Si (100) substrates, in conjunction with electron beam lithography and lift-off techniques. Magnetic hysteresis loops were measured at room temperature using the magneto-optical Kerr effect (MOKE) magnetometer with a 632 nm HeNe laser having a 30 μm spot-size, capturing the reversal behavior of ~5,000 ellipses32. The magnetic field was applied parallel to the major axis of the ellipses. Each measurement was averaged over ~103 cycles at a rate of 11 Hz. The arrays were coated with a 60 nm ZnS layer to improve the signal-to-noise ratio33. FORC measurements were performed as follows22: from positive saturation the magnetic field is swept to a reversal field HR, where the magnetization M(H, HR) is measured under increasing applied field H back to saturation, tracing out a FORC. The process is repeated for decreasing reversal field HR30.
Ellipses were modeled as dipoles oriented parallel to their major axes. The inter-dipole spacing and magnetic moment per dipole in the 100 × 100 array were representative of the experimental system. Each dipole i was assigned an intrinsic coercivity HKi with a distribution experimentally determined from the sample having the weakest interactions, A3. The Hinti dipolar interaction fields at dipole i were calculated on the mean-field level as αM(H), where α was calibrated such that αMS equals the analytically calculated Hint at saturation. This mean-field formulation was extended by the first term of a cluster expansion, representing the nearest neighbor dipole interaction Hnni explicitly: Hinti = αM(H)+Hnni. At each field step (ΔH = 1Oe) the total field Htoti= H+Hinti was compared to HKi, down-flipping occurred when H+Hinti < −HKi and up-flipping occurred when H+Hinti > HKi, until all dipoles became stable.
References
Bader, S. D. Colloquium: Opportunities in nanomagnetism. Rev. Mod. Phys. 78, 1 (2006).
Sun, S. H., Murray, C. B., Weller, D., Folks, L. & Moser, A. Monodisperse FePt nanoparticles and ferromagnetic FePt nanocrystal superlattices. Science 287, 1989–1992 (2000).
Ross, C. Patterned magnetic recording media. Annu. Rev. Mater. Res. 31, 203–235 (2001).
Richter, H. J. et al. Recording potential of bit-patterned media. Appl. Phys. Lett. 88, 222512 (2006).
Engel, B. N. et al. A 4-Mb toggle MRAM based on a novel bit and switching method. IEEE Trans. Magn. 41, 132–136 (2005).
Gallagher, W. J. & Parkin, S. S. P. Development of the magnetic tunnel junction MRAM at IBM: From first junctions to a 16-Mb MRAM demonstrator chip. IBM J. Res. & Dev. 50, 5–23 (2006).
Cowburn, R. P. & Welland, M. E. Room Temperature Magnetic Quantum Cellular Automata. Science 287, 1466–1468 (2000).
Imre, A. et al. Majority Logic Gate for Magnetic Quantum-Dot Cellular Automata. Science 311, 205–208 (2006).
Jain, S., Adeyeye, A. O. & Singh, N. Spin re-orientation in magnetostatically coupled Ni80Fe20 ellipsoidal nanomagnets. Nanotechnology 21, 285702 (2010).
Kou, X. et al. Memory Effect in Magnetic Nanowire Arrays. Adv. Mater. 23, 1393 (2011).
Vedmedenko, E. Y., Mikuszeit, N., Oepen, H. P. & Wiesendanger, R. Multipolar Ordering and Magnetization Reversal in Two-Dimensional Nanomagnet Arrays. Phys. Rev. Lett. 95, 207202 (2005).
Wang, R. F. et al. Artificial ‘spin ice’ in a geometrically frustrated lattice of nanoscale ferromagnetic islands. Nature 439, 303–306 (2006).
Zhang, S. et al. Perpendicular Magnetization and Generic Realization of the Ising Model in Artificial Spin Ice. Phys. Rev. Lett. 109, 087201 (2012).
Gliga, S., Kákay, A., Hertel, R. & Heinonen, O. G. Spectral Analysis of Topological Defects in an Artificial Spin-Ice Lattice. Phys. Rev. Lett. 110, 117205 (2013).
Aign, T. et al. Magnetization Reversal in Arrays of Perpendicularly Magnetized Ultrathin Dots Coupled by Dipolar Interaction. Phys. Rev. Lett. 81, 5656 (1998).
Valcu, B. F., Gilbert, D. A. & Liu, K. Fingerprinting Inhomogeneities in Recording Media using the First Order Reversal Curve Method. IEEE Trans. Magn. 47, 2988 (2011).
Liu, Z. et al. Detecting single nanomagnet dynamics beyond the diffraction limit in varying magnetostatic environments. Appl. Phys. Lett. 98, 052502 (2011).
Mayergoyz, I. D. Mathematical Models of Hysteresis. (Springer-Verlag, New York, 1991).
Pike, C. R., Roberts, A. P. & Verosub, K. L. Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 85, 6660–6667 (1999).
Katzgraber, H. G. et al. Reversal-field memory in the hysteresis of spin glasses. Phys. Rev. Lett. 89, 257202 (2002).
Stancu, A., Pike, C., Stoleriu, L., Postolache, P. & Cimpoesu, D. Micromagnetic and Preisach analysis of the First Order Reversal Curves (FORC) diagram. J. Appl. Phys. 93, 6620 (2003).
Davies, J. E. et al. Magnetization reversal of Co/Pt multilayers: Microscopic origin of high-field magnetic irreversibility. Phys. Rev. B 70, 224434 (2004).
Davies, J. E., Wu, J., Leighton, C. & Liu, K. Magnetization Reversal and Nanoscopic Magnetic Phase Separation in La1-xSrxCoO3 . Phys. Rev. B 72, 134419 (2005).
Pike, C., Ross, C., Scalettar, R. & Zimanyi, G. First-order reversal curve diagram analysis of a perpendicular nickel nanopillar array. Phys. Rev. B 71, 134407 (2005).
Beron, F., Carignan, L. P., Menard, D. & Yelon, A. Magnetic Behavior of Ni/Cu Multilayer Nanowire Arrays Studied by First-Order Reversal Curve Diagrams. IEEE Trans. Magn. 44, 2745–2748 (2008).
Schrefl, T. et al. First order reversal curve studies of permanent magnets. J. Appl. Phys. 111, 07A728 (2012).
Dobrota, C.-I. & Stancu, A. What does a first-order reversal curve diagram really mean? A study case: Array of ferromagnetic nanowires. J. Appl. Phys. 113, 043928 (2013).
Ramírez, J. G., Sharoni, A., Dubi, Y., Gómez, M. & Schuller, I. K. First-order reversal curve measurements of the metal-insulator transition in VO2: Signatures of persistent metallic domains. Phys. Rev. B 79, 235110 (2009).
Krivoruchko, V., Melikhov, Y. & Jiles, D. Relationship between hysteretic behavior of magnetization and magnetoresistance in half-metallic ferromagnets. Phys. Rev. B 77, 180406(R) (2008).
Supplemental material includes family of FORCs and FORC distributions for all arrays, as well as DC-demagnetized configurations for systems with mean-field and nearest neighbor interactions.
Beron, F., Menard, D. & Yelon, A. First-order reversal curve diagrams of magnetic entities with mean interaction field: A physical analysis perspective. J. Appl. Phys. 103, 07D908 (2008).
Dumas, R. K., Gredig, T., Li, C.-P., Schuller, I. K. & Liu, K. Angular dependence of vortex-annihilation fields in asymmetric cobalt dots. Phys. Rev. B 80, 014416 (2009).
Gibson, U. J., Holiday, L. F., Allwood, D. A., Basu, S. & Fry, P. W. Enhanced Longitudinal Magnetooptic Kerr Effect Contrast in Nanomagnetic Structures. IEEE Trans. Magn. 43, 2740 (2007).
Acknowledgements
This work was supported by NSF (ECCS-0925626, DMR-1008791, ECCS-1232275) and BaCaTec (A4 [2012-2]). Work at UCM and IMDEA was supported by the Spanish MINECO grant FIS2008-06249 and CAM grant S2009/MAT-1726.
Author information
Authors and Affiliations
Contributions
D.A.G. obtained the experimental and simulation results and wrote the first draft of the paper. G.T.Z. and M.W. participated in the simulation design. R.K.D., A.G., N.E., J.L.V. and K.L. participated in the experimental design, fabrication and characterization. K.L. and G.T.Z. designed and coordinated the whole project. All authors contributed to analysis, discussion and revision of the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplemental Materials
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Gilbert, D., Zimanyi, G., Dumas, R. et al. Quantitative Decoding of Interactions in Tunable Nanomagnet Arrays Using First Order Reversal Curves. Sci Rep 4, 4204 (2014). https://doi.org/10.1038/srep04204
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep04204
This article is cited by
-
Reconstructing phase-resolved hysteresis loops from first-order reversal curves
Scientific Reports (2021)
-
Facile decoding of quantitative signatures from magnetic nanowire arrays
Scientific Reports (2020)
-
Relation of the average interaction field with the coercive and interaction field distributions in First order reversal curve diagrams of nanowire arrays
Scientific Reports (2020)
-
Growth and magnetic interaction of single crystalline Ni gradient–diameter magnetic nanowire arrays
Journal of Materials Science (2019)
-
Study on magnetic properties of NiFe/Cu multisegmented nanowire arrays with different Cu thicknesses via FORC analysis: coercivity, interaction, magnetic reversibility
Journal of Materials Science: Materials in Electronics (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.