Introduction

Quantum physics differs significantly from classical physics in many aspects. A complete classical description of an object contains information concerning only compatible properties, while a complete quantum description of an object also contains complementary information concerning incompatible properties (see Fig. 1). This difference is also present in correlations. A classical correlation in a bipartite system involves the correlation of only a certain property, while a quantum correlation in a bipartite system also involves complementary correlations of incompatible properties. The simultaneous existence of complementary correlations together with the freedom to select which one to extract is the most important feature of quantum correlation (see Fig. 2). Schrödinger introduced the word “entanglement” to describe this peculiar feature, which was termed “spooky action at a distance” by Einstein1,2,3,4.

Figure 1
figure 1

(a) A complete classical description of a classical object (a giraffe) is a simple collection of information about compatible properties, such as color, height, weight, position and velocity (the photo was taken by S.W. in Hefei animal zoo). (b) A complete quantum description (a quantum state |ψ〉) of a quantum system (e.g. a spin-1/2 particle) contains information about incompatible properties (σx, σy, σz) in an intrinsic way: information about incompatible properties exists simultaneously even though only a single property can be measured at a time; and we can freely select which property to measure.

Full size image
Figure 2
figure 2

(a) Classical correlation in a bipartite state reaches the maximum in a certain basis and vanishes in any complementary basis. (b) However, quantum correlation in a bipartite state contains correlations in complementary bases simultaneously; and one can freely select with which basis to read out the correlation.

Full size image

More recently, entangled states were defined as states that cannot be written as convex sums of product states. This precise definition is very helpful in terms of both mathematical and physical convenience and it motivates the useful definition of the entanglement of formation. However, we now know that entanglement of formation is just one particular aspect of quantum correlation. Many measures of quantum correlation have been proposed from different perspectives and they can be divided into two categories: entanglement measures5,6,7,8,9 and measures of nonclassical correlation beyond entanglement10,11,12,13,14,15,16,17,18,19,20,21,22,23,24.

The essential feature of quantum correlation, i.e., the simultaneous existence of complementary correlations in different bases, is also revealed by the Bell's inequalities25,26. Bell's inequalities quantify quantum correlation via expectation values of local complementary observables. Instead, we shall seek a way to directly reveal the essential feature of quantum correlation from an information-theoretical perspective. Indeed, there are several previous entropic measures of quantum correlation (such as quantum discord D, measurement-induced disturbance, symmetric discord, etc), which are proposed from an information-theoretical perspective. But these measures are based on the difference between quantum mutual information27 (which is assumed as the total correlation) and a certain measure of classical correlation. Here, we take a different approach and reveal the essential feature of quantum correlation directly. The genuine quantum correlation does not vanish under a change of basis and can be characterized as the residual correlations remaining in the complementary bases.

Results

The idea

We begin with a comparison between the correlations in two different states:

The first state has only classical correlation, which can be revealed when Alice and Bob each measure the observable σz, i.e., project their qubits onto the basis {|0〉, |1〉}. If they measure a complementary observable, σx or σy, no correlation between their measurement results exists. The second state is the Einstein-Podolsky-Rosen (EPR) state (or the singlet state), which has both classical and quantum correlations. The classical correlation in the EPR state can be revealed when Alice and Bob each measure the same observable, e.g. σz. Moreover, this kind of correlation also exists simultaneously in complementary bases (actually, in all bases). The simultaneous existence of correlation in complementary bases is an essential feature of the genuine quantum correlation. This feature is illustrated in Fig. 2 and treated in a rigorous manner in the rest of this article.

Classical and genuine quantum correlations

For any bipartite quantum state ρAB, there are many measures of classical correlation28. Here, we use the one proposed by Henderson and Vedral29, which is also used in the definition of quantum discord10. Alice selects a basis of her system in a dA-dimensional Hilbert space and performs a measurement projecting her system onto the basis states. With probability , Alice will obtain the i-th basis state |ai〉 and Bob's system will be left in the corre sponding state . The Holevo quantity of the ensemble {pi; } that is prepared for Bob by Alice via her local measurement is given by , which denotes the upper bound of Bob's accessible information about Alice's measurement result when Alice projects her system onto the basis {|ai〉A}. The classical correlation in the state ρAB is defined as the maximal Holevo quantity over all local projective measurements on Alice's system:

A basis {|ai〉A} that achieves the maximum C1(ρAB) is called a C1-basis of ρAB and is denoted as . There could exist many C1-bases for a state ρAB.

We consider another basis , which is mutually unbiased to the C1-basis in the sense that , i.e., if the system is in a state of one basis, a projective measurement onto the mutually unbiased basis (MUB) will yield each basis state with the same probability. The most essential feature of quantum correlation is that when Alice performs a measurement in another basis that is mutually unbiased to the C1 basis, Bob's accessible information about Alice's results, characterized by the Holevo quantity, does not vanish. This residual correlation represents genuine quantum correlation and can be used as a measure of the quantum correlation. Formally, a measure of quantum correlation Q2(ρAB) in the state ρAB is defined as the Holevo quantity of Bob's accessible information about Alice's results, maximized over Alice's projective measurements in the bases that are mutually unbiased to a C1-basis and further maximized over all possible (if not unique), i.e.,

where is any basis mutually unbiased to the basis . A basis that achieves the maximum quantum correlation Q2 in (4) is called a Q2-basis and is denoted as . If there is only one C1-basis, the second maximization over the C1-bases in (4) is not necessary. If there is more than one C1-basis and not all of them achieve the maximum in (4), then we redefine the C1-bases as those that also achieve the maximum in (4). In other words, the bases (if any) that achieve the maximum in (3) but do not achieve the maximum in (4) will not be considered as any more. After this redefinition, if is still not unique, then depends on the choice of . It is also obvious that is mutually unbiased to .

Similar to the case of characterizing entanglement, a single quantity is not sufficient to describe the full property of quantum correlation because there could be many types of quantum correlation. Following the same line of reasoning, we can define the residual correlation in a third MUB as

where is any basis mutually unbiased to both and . An optimum basis to achieve the maximum in (5) is called a Q3-basis and is denoted as . Similarly, we redefine the Q2-bases as those that are optimum in both (4) and (5) and further redefine the C1-bases as those that are optimum in (3), (4) and (5).

Suppose in this manner that we can define M quantities for the measures of correlation, which are conveniently written as a single correlation vector for the state ρAB. The number M cannot be greater than the number of MUBs that exist in the dA-dimensional Hilbert space. The first quantity C1 denotes the maximal classical correlation present in the state ρAB, which can be revealed when Alice performs a measurement of her system in a C1-basis . As classical correlation will vanish when measured in a mutually unbiased basis, all of the other quantities describe genuine quantum types of correlation. The second quantity Q2 denotes the maximal genuine quantum correlation and denotes an optimum basis to reveal this correlation. The third quantity Q3 denotes another type of genuine quantum correlation and denotes a basis to reveal the second type of quantum correlation.

The splitting of the correlation vector as a single classical component (C1) and several quantum components (Q2, , QM) is not artificial, in fact, this splitting captures the essential difference between classical correlation and quantum correlation. The quantity C1 represents the maximal amount of correlation available in a single basis . The quantity Q2 represents the maximal amount of correlation that is available not only in the first basis but also in a second complementary basis (we know from the definition of these quantities). And Q3 represents the maximal amount of correlation available not only in and , but also in a third MUB . The amount Q3 of correlation exists in 3 MUBs while the amount Q2 of correlation may only exist in 2 MUBs. Thus, Q3 represents the amount of correlation with a higher level of quantumness than that of Q2 and may have more practical advantages when 3 MUBs are necessarily used (e.g. entanglement-based QKD via 6-state protocol).

It should be pointed out that the maximum number of MUBs that exist in a dA-dimensional Hilbert space is not known for the general case. When dA is a power of a prime number, a full set of dA + 1 MUBs exists; for other cases, there may not exist dA + 1 MUBs. For example, when dA = 6, only 3 MUBs have been found yet, while 3 is much less than dA + 1 = 7. Many interesting works can be found on the existence of MUBs in the literature30,31,32,33,34. Since there exist at least 3 MUBs for any integer dA ≥ 2, the quantities C1, Q2 and Q3 are well-defined for any dA ≥ 2. In many cases, we are interested in combined systems of qubits with dA being a power of 2, thus, dA + 1 MUBs exist and quantities are all well-defined. For an arbitrary dA-dimensional Hilbert space, we don't make assumptions about the maximal number of MUBs that exist, we only assume that M MUBs are available, where M is less or equal to the maximal number of MUBs that exist. In many cases, we only discuss the first 3 elements (C1, Q2 and Q3) of the correlation vector for simplicity.

Examples

Now, we shall calculate the correlation vector for several families of bipartite states and see how these measures in terms of MUBs are well justified as measures of classical and genuine quantum correlations.

For a bipartite pure state written in the Schmidt basis, , the maximal classical correlation can be revealed when Alice performs her measurement onto her Schmidt basis {|ai〉}; thus, one immediately has . If Alice chooses another basis , whenever she obtains a particular measurement result, Bob will be left with a pure state. Therefore, one can easily obtain the maximal true quantum correlation Q2 = S(ρB) = C1; any other basis will yield the same amount of quantum correlation. Therefore, the correlation vector for a bipartite pure state |ψ〉AB is given as . The correlation vector exhibits a unique feature of the correlations in a pure state: the classical correlation is equal to the quantum correlation revealed in any basis and both values are equal to the von Neumann entropy of the reduced density matrix on either side, which is the usual measure of entanglement in a pure state.

A classical-quantum (CQ) state is a bipartite state that can be written as

where {qi} is a probability distribution, is a basis of system A in a dA-dimensional Hilbert space and {σi} is a set of density matrices of system B. The maximal classical correlation is revealed when Alice performs her measurement in the basis {|i〉}12; thus, the maximal classical correlation in the CQ state ρcq is given by . To calculate the amount of quantum correlation, Alice projects her system onto another basis that is mutually unbiased to the optimum basis {|i〉} for classical correlation. From , we have

For each different result j that Alice obtains, Bob is left with the same state ; thus, Bob's state has no correlation with Alice's result and we immediately have according to the definitions of these quantities. Hence, for a CQ state, the correlation vector is given as . The only correlation present in a CQ state is the classical correlation and the quantum correlation in any MUB vanishes!

Next, we consider the Werner states of a d × d dimensional system35,

where −1 ≤ α ≤ 1, I is the identity operator in the d2-dimensional Hilbert space and is the operator that exchanges A and B. Because the Werner states are invariant under a unitary transformation of the form , the maximal classical correlation can be revealed when Alice simply projects her system onto the basis states {|i〉}. With probability , Alice will obtain the i-th basis state |i〉 and Bob will be left with the state . It is straightforward to show that . Due to the symmetry of the Werner states, it is not difficult to demonstrate that . Therefore, for the Werner state ρw, the correlation vector is given by . The maximal quantum correlation in a Werner state can be revealed in any basis and it is equal to the maximal classical correlation C1. However, the correlation vector of a Werner state is different from that of a pure state because C1 ≤ S(ρB) = log2d. The inequality becomes an equality only when d = 2 and α = 1, in which case, the Werner state becomes a pure state ρw = |EPR〉 〈EPR|. For the Werner states, the symmetric discord is equal to the quantum discord D12 when Alice's measurement is restricted to projective measurements. The entanglement of formation Ef for the Werner states is given as , with h(x) ≡ −x log2x − (1 − x) log2(1 − x)36. The three different measures of quantum correlation, i.e., our measure of maximal quantum correlation Q2, the quantum discord D and the entanglement of formation, are illustrated in Fig. 3 for comparison. From this figure, we see that the curve for entanglement of formation intersects the other two curves; thus, Ef can be larger or smaller than Q2 (D).

Figure 3
figure 3

Three measures of quantum correlation for the Werner states as functions of α when d = 2 (left) and d = 3 (right).

The red curve represents our measure Q2, the green curve represents the quantum discord D and the blue curve represents the entanglement of formation Ef.

Full size image

As the last example, we consider a family of two-qubit states, where the reduced density matrices of both qubits are proportional to the identity operator. Such a state can be written in terms of Pauli matrices,

where I2 is the identity operator in the two-dimensional Hilbert space of a qubit and wjk are real numbers that satisfy certain conditions to ensure the positivity of the matrix in (9). These two-qubit states can be transformed by a local unitary transformation (that does not change the correlations) to the following form:

which is equivalent to the Bell-diagonal states. To ensure the positivity of the matrix in (10), the real vector must lie inside or on the boundary of the regular tetrahedron that is the convex hull of the four points: (−1, −1, −1), (−1, 1, 1), (1, −1, 1) and (1, 1, −1) (which are the four Bell states). The singular values of the matrix wjk are given by |rj|. We rearrange the three numbers {r1, r2, r3} according to their absolute values and denote the rearranged set as {, , } such that .

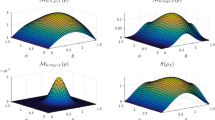
In the Methods, we prove that the correlation vector of the state in (9) is given by , where with h(x) ≡ −x log2x − (1 − x) log2(1 − x). To have some intuition of this result, we consider some special classes of states with only one parameter. When with −1 ≤ α ≤ 1, the states in (10) become the Werner states for d = 2 in (6). When r1 = r2 = 1 − 2p and r3 = −1 with 0 ≤ p ≤ 1, the states in (10) become ρ1 = p|ψ−〉 〈ψ−| + (1 − p) |ψ+〉 〈ψ+|; we obtain C1 = 1 and Q2 = Q3 = 1 − h(p). When r1 = 1 − 2p and r2 = r3 = −p, the states in (10) become ; we have , and . Here, , and . Our measure of quantum correlation Q2 is compared with the quantum discord D and the entanglement of formation Ef for ρ1 and ρ2 in Fig. 4.

Figure 4
figure 4

Different measures of quantum correlation for two special classes of states: ρ1 = p |ψ−〉 〈ψ−| + (1 − p) |ψ+〉 〈ψ+| (left) and (right).

In each figure, the red curve represents our measure Q2, the green curve represents the quantum discord D and the blue curve represents the entanglement of formation Ef. In the left figure, the green curve is not shown because D = Q2 for ρ1.

Full size image

Inequality relations between correlation measures

It is not difficult to show that the relation Q2 ≤ D holds for the Werner states and for all the example states considered in this article. However, it is not clear whether this inequality holds for any bipartite states. If Q2 ≤ D holds for any bipartite states, then one can easily have C1 + Q2 ≤ S(A:B) where S(A:B) = S(ρA) + S(ρB) − S(ρAB) denotes the quantum mutual information.

Nevertheless, we can prove the following inequality:

where Hγ (γ = 1, 2) denotes the Shannon entropy of the probability distribution obtained by the measurement on system A in the basis . The proof is given in the Methods. Since Hγ ≤ log2dA, one immediately has

As C1 and Q2 are the two largest elements in the correlation vector, when they are replaced by correlations in any two MUBs, inequalities (11) and (12) still hold.

Discussion

Our measures of quantum correlation provide a natural way to quantify the “spooky action at a distance” and directly reveal the essential feature of the genuine quantum correlation, i.e., the simultaneous existence of correlations in complementary bases. This feature enables quantum key distribution with entangled states, since the quantum correlation that exists simultaneously in two (k) MUBs, which is quantified by Q2 (Qk), is the resource for entanglement-based QKD via two (k) MUBs. Quantitative relation between the genuine quantum correlation and the secret key fraction in QKD could be studied in further work.

All the measures considered above are not symmetric with respect to the exchange of systems A and B, as only system A's bases are considered to reveal the correlation. Symmetric measures and a symmetric correlation vector are also introduced and discussed in the Methods. A further study of the relation between the symmetric correlation vector and the symmetric discord12 could reveal the difference between these measures in practical applications.

There are some open questions. Are our measures (Q2, Q3) of genuine quantum correlation additive? How do they behave under some natural operations (for example, Alice adds an ancilla)? Do our measures (Q2, Q3) behave like the entanglement measures that do not increase under local operations and classical communication (LOCC)9, or more like the measures of nonclassical correlation beyond entanglement (for example, quantum discord) that could increase under LOCC38? We hope that further investigations will unveil these mysteries.

Methods

Proof of the inequality (11)

Here we prove inequality (11) in the main text.

Let denote the probability distribution obtained by the measurement on system A in the basis , i.e., . Let Hγ (γ = 1, 2) denote the Shannon entropy of the probability distribution, . Here, the basis is the optimum basis for measurement on system A to achieve the maximum classical correlation C1 and the basis is the optimum basis to achieve Q2 among the bases that are mutually unbiased to . However, the proof below only requires that and are mutually unbiased to each other.

Let with γ = 1, 2, where .

The uncertainty relation37 gives

where S(A|B) = S(ρAB) − S(ρB) and . As ρ(γ) is a CQ state, one can show that . Therefore,

As and , we immediately have

which completes the proof of the inequality.

Calculation of the correlation vector for the states in (9)

In this paragraph, we shall demonstrate that the correlation vector of the state in (9) is given by , where with h(x) ≡ −x log2x − (1 − x) log2(1 − x). We perform the calculation in the transformed basis, with the states rewritten in Eq. (10). Without loss of generality, we can suppose the numbers rj are already arranged according to |r1| ≥ |r2| ≥ |r3|; then, we only need to prove that , where . A projective measurement performed on qubit A can be written , parameterized by the unit vector . We have

When Alice obtains ±, qubit B will be in the corresponding states , each occurring with probability . The entropy reaches its minimum value when . From and S(ρB) = 1, we immediately have . The basis for Alice's projection in the definition of Q2 must be mutually unbiased to the basis parameterized by ; therefore, the unit vector must be in the form . The maximum in the definition of Q2 is reached when and thus a calculation similar to that for C1 yields . For a qubit system, three MUBs exist. We can reveal the quantum correlation in another (the last) MUB, which corresponds to the case . We easily obtain . For the general case in which the numbers rj do not follow |r1| ≥ |r2| ≥ |r3|, a similar argument yields with .

Symmetric correlation vector

The correlation vector defined in the main text relies on a special choice of the measure of classical correlation; it is not symmetric with respect to exchange of A and B. Here, we consider an alternative definition of the correlation vector, which is symmetric with respect to the exchange of A and B.

For any bipartite quantum state ρAB, Alice chooses a basis of her system in a dA-dimensional Hilbert space and Bob chooses a basis of his system in a dB-dimensional Hilbert space and each one performs a measurement projecting his/her system onto the corresponding basis states. With probability , Alice and Bob will obtain the i-th and j-th results, respectively. The correlation of their measurement results is well characterized by the classical mutual information:

where H {pk} is the Shannon entropy of the probability distribution {pk} and and are the marginal probability distributions. In other words, and .

The symmetric measure of classical correlation in the state ρAB is defined as the maximal classical mutual information of the local measurement results, maximized over all local bases for both sides, i.e.,

The symmetric measure of classical correlation was discussed in12 (where the notation Imax was used). A product basis that achieves the maximum in (18) is called a -basis and is denoted as .

The symmetric measure of maximal quantum correlation is defined as the maximal residual correlation over all local bases that are mutually unbiased to a -basis , further maximized over all possible -bases (if not unique), i.e.,

where is mutually unbiased to and . A basis that achieves the maximum in (19) is called a -basis and is denoted as . We redefine the -bases as the bases that achieve the maximum in (18) as well as the maximum in (19).

Similarly, denotes the residual quantum correlation in a third complementary basis that is mutually unbiased to both and . In this manner, we have an alternative correlation vector , which is symmetric with respect to the change of A and B.

Because the Holevo bound is an upper bound of accessible classical mutual information, we immediately know from the above definitions that the asymmetric correlation vector is an upper bound of the symmetric correlation vector for each component, i.e., , , , . It is not difficult to demonstrate that the asymmetric correlation vector actually coincides with the symmetric correlation vector (i.e., ) for the CQ states, the Werner states and the two-qubit states in Eq. (9).