Introduction

One of the most important problems in astrophysics is the acceleration of charged particles to very high energies, e. g. to explain the cosmic ray spectrum1,2, where shock acceleration is a very promising model for the power-law dependence at high energies, or the jet emission of particles in gamma-ray bursts3. The acceleration process in collisionless shocks is determined by the underlying microphysics and depends on the shock character, i. e. the electromagnetic fields are responsible for sustaining the shock transition, since in collisionless shocks the dissipation mechanism is determined only by the fields in the shock front and not by the inter-particle collisions since the mean free path is much larger than the shock front. For instance, cold electron distributions can lead to electromagnetic shocks4,5, while low flow velocities lead to electrostatic shocks6, but the transition between the two different regimes and the parameter space where the different field structures dominate have not been defined yet.

Electromagnetic shocks are mediated by Weibel-type instabilities7,8 with the shock front transition determined by magnetic fields on the ion scale (). They usually appear in astrophysical scenarios, e. g. in the outflows of gamma-ray bursts, active galactic nuclei or pulsar wind nebulae. Since instabilities of the Weibel-type are very efficient in highly anisotropic plasmas, low thermal and high fluid velocities enhance the shock formation process9. The study of electromagnetic shocks in the laboratory is difficult because of the long shock formation time at low fluid velocities10, which are now obtained experimentally11,12, or the need to drive relativistic speeds, which requires very intense lasers34.

Electrostatic shocks, on the other hand, are a consequence of non-linear wave steepening and wave breaking of ion-acoustic modes and they are more relevant for laboratory experiments, e. g. in laser-plasma interactions14,15, fast ignition16 and lately also for medical applications17 as alternative to standard laser-acceleration schemes18,19,20. The shock formation process is enhanced in plasmas with high mass and temperature ratios between the negatively and positively charged plasma components6,21. Theoretical estimates are usually one-dimensional and neglect the importance of electromagnetic modes which are clearly associated with the multi-dimensional features of the problem.

Shocks naturally appear from the collision of two plasma slabs and are of electromagnetic character if transverse electromagnetic modes drive the shock formation process or of electrostatic character if longitudinal instabilities dominate. However, the shock character can change on long time scales due to competing wave processes, which has been phenomenologically identified in numerical simulations22,23. The shocks will have different microphysics and lead to distinct spectra of accelerated particles. It is thus necessary to understand the dependence of the character of the shock on the flow to design laboratory experiments to clarify the underlying physics and to connect with astrophysics observations.

In this paper, we provide a theoretical prediction of the dominant shock character for the two main parameters characterising non-magnetised plasma flows. We determine regimes depending on the upstream parameters and identify a region, where the transition from initially electrostatic shocks to electromagnetic shocks occurs. The theoretical findings are confirmed with particle-in-cell simulations and the transition between the different regimes is illustrated. Connections with possible experiments are made and we show that these distinct regimes can already be explored in the laboratory.

Results

Our starting point is the analytical description of electrostatic shocks. This is a classical problem6,21,24,25,26,27,28,29 for which there are analytical solutions, in 1D, for the shock solution. We will use this solution to verify under which conditions the growth rate of electromagnetic Weibel modes associated with the distribution function is larger than the inverse electrostatic shock formation time. We first observe that an electrostatic shock solution exists. Applying Poisson's equation to connect the electrostatic potential and densities of the upstream and downstream shock regions and treating the potential as a harmonic oscillator in the so-called Sagdeev potential24 provides the valid shock solutions, which are limited by a maximum Mach number. The criterion still holds in the relativistic generalisation and thus an electrostatic shock is formed if the relativistic Mach number with u0 = β0γ0 the proper upstream velocity, and the ion sound speed with Te the initial electron temperature6,31. This can be expressed as kBTe/mec2 = ((3.1/u0)2 + 1)−1 mi/me and establishes a first domain of the u0 − Te par- ameter space where shocks can be explored. From the growth rate for longitudinal modes for cold ions30, the shock formation time is estimated as , which we have confirmed in a series of electrostatic shock simulations.

We now analyse the stability properties of the electrostatic shock solutions regarding the growth of transverse electromagnetic modes. We assume that the particle distribution after electrostatic shock formation is given by the model described in Schamel (1972)29, with the corresponding generalisation for relativistic beams31. All quantities are given in the laboratory frame, which corresponds to the rest frame of the downstream population. The upstream populations of free streaming electrons and ions are affected by the shock potential, leading to a population of free streaming and trapped electrons downstream. Throughout the paper the ion populations are kept cold and we assume that the impact on their distribution is negligible at this stage. We consider here the simplest case of equal density and temperature ratios of the upstream and downstream populations, so that the free electron distribution is given by a drifting Maxwell-Jüttner distribution , where is the proper bulk velocity of the upstream in the shock frame, with propagation direction along the x axis, μ = mec2/kBTe is the thermal parameter and φ = eϕ/mec2 the electrostatic potential. This distribution is valid if the kinetic energy exceeds the potential energy, leading to the condition for the Lorentz factor, where fe,r+ is valid for ux < −uc and fe,r− for ux > uc with . In the non-relativistic limit, this distribution is given by with . The electrons are trapped if their kinetic energy is lower than the energy of the electrostatic potential, . In analogy to the non-relativistic approach, where the trapped population is described with a flat-top profile21,29, we formulate the relativistic distribution of trapped particles as with , which goes to in the non-relativistic approximation.

The dispersion relation of electromagnetic filamentation/Weibel modes is calculated (outlined in the supplementary information) and a numerical solution can be found for the general (relativistic) case. In the non-relativistic approximation, , the dispersion relation can be approximated by

with frequency ω, wave number k, plasma dispersion function Z32 and , resembling the well-known dispersion relation for the Weibel instability7, where the potential-dependent term plays the role of the anisotropy parameter A, with . This anisotropy is introduced by the distortion of the distribution function in the longitudinal direction due to the electrostatic field in the shock. The growth rate is defined as the imaginary part of the frequency . In the case and , the approximation can be found. For small arguments of the Z function, which is the case for very low fluid velocities and thermal velocities the growth rate is given by with and a maximum growth rate

The Weibel modes are considered to be relevant if their time scale is comparable with the electrostatic shock formation time scale . The growth rate depends on the potential across the shock front and decreases from the upstream to the downstream. In order to define parameter regimes specifically, it is assumed that ion reflection from the potential has just set in, which is equivalent to consider . The details about the dependence of the growth rate of the Weibel modes across the shock front and with the potential will be presented elsewhere.

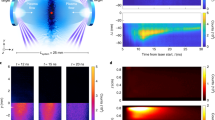
As a result of the theoretical analysis, parameter regimes of the dominating electrostatic or electromagnetic shock character can be defined, which are summarised in Figure 1. The region of purely electromagnetic shocks (EM), which is determined by the electrostatic shock formation condition 6 and purely electrostatic shocks (ES) are separated by a transition region (ES → EM), where the growth rate of the Weibel instability is larger than the shock formation time scale.

Figure 1
figure 1

Definition of electrostatic, electromagnetic and transition regimes depending on input parameters kBTe/mec2 and proper flow velocity u0 = β0γ0.

The electrostatic shock formation condition6 (red dashed line) limits the parameter space of electromagnetic shocks (EM). The blue line represents the condition tW = tsf with the nonrelativistic approximation in dashed, separating the region of purely electrostatic shocks (ES) and the transition region (ES → EM). The black dots represent the sub-set of simulation parameters discussed in the paper.

Full size image

The transition between the different regimes, shown in Figure 1, can be observed in particle-in-cell simulations with details given in the Methods section and we discuss in detail the three representative cases kBTe/mec2 = 10, 3.5, 0.5 with proper flow velocity u0 = 0.1. The role of the cold ion-ion instability has been addressed in Fiuza et al. (2012)13.

In the electrostatic regime (ES) and for kBTe/mec2 = 10, after the potential energy in the shock front exceeds the kinetic energy of the upstream protons and goes into a steady state with a downstream to upstream density ratio nd/n0 = 2.7 and shock speed vsh = 0.048 c and a second peak behind the shock propagating with 0.041 c, in agreement with31. The potential energy is much larger than the proton kinetic energy, so that most of the upstream protons are reflected back into the upstream and a quasi monoenergetic spectrum is created, clearly illustrating the distinct features of ion acceleration in electrostatic shocks.

The electromagnetic shock (EM) evolves on much longer time scales and protons thermalise only on thousands . The two counter propagating plasma slabs just interpenetrate and overlap each other, until the filamentation instability starts to slow down the protons. The electrostatic potential across the shock is not strong enough to reflect them and ion acceleration occurs on a much longer time scale in a Fermi-like process4,5.

In the transition region (ES → EM), we observe two stages. In the first stage, a strong electrostatic field appears and a shock is formed, showing the characteristics of an electrostatic shock. The potential energy is on the order of the upstream kinetic energy and most of the protons are reflected, such that a quasi monoenergetic spectrum of ions is formed. At approximately a second potential appears at the centre of the box and propagates outwards with a decreased potential jump of 0.6 Ekin,p. Only a fraction of the upstream protons is reflected at the shock front and the proton spectrum becomes more diffuse, see Figure 2. The protons start to thermalise in the downstream region. The shock is now in a quasi-steady state, after , with a decreased shock velocity 0.022 c and the density ratio increases to approximately 333. The potential jump becomes less sharp and the shock front region extends to larger spatial scales with the same order of potential difference between the upstream and downstream region. The shock front is now determined by a mix of transverse and longitudinal modes, but without the mono energetic features of the ion spectrum.

Figure 2
figure 2

(a) Density in the ES/EM transition case kBTe/mec2 = 3.5 and comparison of 1D (grey) and 2D (black) simulation. Proton phase spaces in 1D (b) and 2D (c). All are shown for tωpe = 104.

Full size image

The transition of the shock formation process between the different regimes is illustrated in Figure 3 at tωpe = 2500. We note that a perpendicular magnetic field B3 appears in all three regimes, but the character changes significantly. In the case of an electrostatic shock (fig. 3 a) the spatial scale is large with a wavelength λ = c/ωpi in the linear phase of magnetic field generation. In the transition case (b) the wavelength is decreased to 0.6 c/ωpi and a more ordered structure appears with filaments aligned with the shock propagation direction x1, which resembles more the ordered structure of the electromagnetic case (c), where the characteristic wavelength is 0.2 c/ωpi, closer to the length scale for electron filamentation. At this stage, the shock has not fully formed yet, but the change in the electron dynamics, which are determining the shock formation process, is clearly visible.

Figure 3
figure 3

Magnetic field B3 in the entire simulation box at early stage of shock formation, tωpe = 2500, for kBTe/mec2 = 10 (a), 3.5 (b) and 0.5 (c).

Overplotted is the electrostatic potential normalised to the ion kinetic energy Eφ/Ekin,p showing the transition from the electrostatic (a) to the electromagnetic case (c).

Full size image

Also the shape and strength of the electrostatic potential are closely connected with the shock character. In the electrostatic case, a potential jump is generated as expected from electrostatic theory29, showing oscillations that indicate particle trapping in the downstream. In the steady state, the energy of the electrostatic potential is Eφ = 1.6 Ekin,p, i.e. high enough to reflect the upstream ions.

In the transition case, a first potential develops which smoothens out while a second potential appears from the center of the box (see fig. 3b). It shows no signs of particle trapping, i. e. oscillations in the downstream potential. The differences in mass and temperature between protons and electrons also lead to a potential in the electromagnetic case Eφ = 0.07Ekin,p, which is so small that almost no protons are reflected from it. The potential jumps for the different scenarios are shown in Figure 4. The ability of ion reflection is increased with the electron temperature. We observe a matching with the regimes defined in Figure 1 since the ion reflection condition Eφ/Ekin,p > 1 coincides with the threshold for purely electrostatic shocks (ES) at around kBTe/mec2 ≈ 7 for u0 = 0.1.

Figure 4
figure 4

Potential energy over ion kinetic energy against kBTe/mec2 measured from simulation data.

The horizontal dashed line represents the ion reflection condition Eφ > Ekin,p. The regions EM, ES → EM, ES are taken from Figure 1 for u0 = 0.1.

Full size image

An analysis of the particle dynamics in the field structure of the shocks supports our findings. To capture the motion in a fully developed shock, here, the electromagnetic case (EM) is presented by a run with a reduced mass ratio and relativistic upstream fluid velocity. Figure 5(a) shows typical proton trajectories for the three different regimes. In the case of an electrostatic shock, the upstream protons are picked up by the shock front and reflected back into the upstream with velocity vi,refl ≈ v0 + 2vsh in the non-relativistic case. These particles gain the highest energies for the time scales in our comparison. In electromagnetic shocks, the particles gain energy by scattering off the electromagnetic turbulences in the shock front region. This scattering process can be well observed in fig. 5(a). In the transition region (ES/EM), the potential is not strong enough to reflect the fast upstream protons and they are decelerated while approaching the shock front. Only the slowest particles are scattered back into the upstream region with velocities much smaller than vi,refl. The accelerated proton spectra in Figure 5(b) thus show fundamental differences. While in the electrostatic case, the velocities are highest and centred with a low spread around the value vi,refl, in the other two regimes the accelerated spectra are broad and centred around lower values.

Figure 5
figure 5

(a) Proton trajectories for the three different regimes defined in Fig. 1 relative to the position of the shock front xsh and colour coded with the longitudinal momentum u1 = p1/mpc, which was normalised to the momentum of the upstream fluid u0 and (b) proton spectra in the downstream and shock front region after the steady state of shock formation.

Full size image

Discussion

In order to make the connection with laser experiments, we now connect the parameters determining the shock character with the laser parameters in laser-solid interactions. We assume that two symmetric counter propagating flows are created by irradiating a plasma target with a laser. This can be done by either using two laser-irradiated foils in order to create two counter streaming flows35, or by using a single high-intensity laser that accelerates the plasma into the target and the return current provides the required counter-streaming conditions for the development of the instability13. In this last scenario, the temperature of the plasma flow Te can be connected with the laser via the ponderomotive scaling of Te with the laser normalised intensity a0 via 36. For the flow velocity, one can use the hole boring velocity as obtained in36, with critical density nc. We observe that the physics of ponderomotive heating and hole boring is quite complex but the approximate scaling laws can provide a guide to the required laser parameters. During the characteristic time of the laser pulse τ, which should be on the order of a few times the electrostatic shock formation time with λ0 the laser wavelength, the plasma slabs overlap for L = 2 v0 τ, which defines the minimum length for the target thickness. For geometrical reasons and in order to guarantee the shock front to be as plane as possible, the laser focal spot size should be large compared with the shock front thickness, . Simulations show that the hole boring process is connected with a non-regular pile up of the density39. For simplicity, we assume a homogeneous initial density distribution with n0/nc = 1–50 and plan to address the modifications due to a realistic smoothly growing density profile in a future work. Assuming a laser wavelength λ0 = 1 μm and a0 ≈ 5–50, which is in the range of state-of-the-art laser systems and ongoing laser experiments, the shock formation time is on the ps time scale with a target size of 10–100 μm. We can expect Te in the range 2–25 MeV and , thus capable of exploring the transition.

Starting from the seminal analytical solution of an electrostatic shock, we have calculated if the system is stable to Weibel or filamentation modes. Due to the distorted electron distribution of free and trapped particles in the downstream of the shock, an anisotropy arises that enhances the excitation of electromagnetic modes. Depending on the initial electron temperature and fluid velocity, parameter regimes were identified in which the shock solution will be purely electrostatic, electromagnetic or shows a transition between the two regimes.

The transition between the different shock characters has been confirmed by particle-in-cell simulations. In the transition regime, a change of the shock character appeared with a shock formation time characteristic for electrostatic shocks. The appearance of a magnetic field was observed in all three cases, with a significantly different character and different temporal and spatial scales. For electrostatic shocks, the temporal and spatial scales of the magnetic field are , c/ωpi; in the transition region it grows on , 0.6 c/ωpi, while for electromagnetic shocks , 0.2 c/ωpi. Furthermore, we found the reflection condition as an alternative criterion for distinguishing between the different regimes, since it matches with the boundary of the pure electrostatic shock regime. The dominant acceleration process in the different regimes, a function of the fields mediating the shock, determines the acceleration spectra of the protons. While in the electromagnetic case a broad spectrum is generated, highest particle velocities with rather small velocity spread are obtained in the electrostatic case. By using standard scaling for the electron temperature and hole boring velocity with the laser intensity, we showed that the relevant regimes discussed in this paper can already be studied with existing laser systems.

Methods

Two-dimensional numerical simulations were carried out with the particle-in-cell code OSIRIS (ref. 37, 38) modelling the shock formation due to two counter streaming plasma flows of electrons and ions. Two sets of simulations have been performed with the fluid velocity of the plasma slabs v0 = ±0.1 c and thermal parameters kBTe/mec2 = 0.5, 3.5, 10, 20 and 50 of a relativistic Maxwell-Juettner distribution. High resolution runs up to were performed with a simulation box covering Lx = 1000 c/ωpe and Ly = 450 c/ωpe and a spatial resolution Δx = Δy = 0.1 c/ωpe to resolve the Debye length. All quantities are normalised to , the non-relativistic electron plasma frequency with respect to the upstream electron density n0,e. In the second set of simulations, the shock evolution was followed up to with a decreased resolution Δx = Δy = 0.5 c/ωpe and the simulation box covering Lx = 8000 c/ωpe and Ly = 200 c/ωpe. All simulations were performed with a realistic proton to electron mass ratio mp/me = 1836. A cubic interpolation scheme and 9 particles per cell and per species were used in all simulations. To obtain the typical particle trajectories in the electromagnetic regime, a simulation with reduced mass ratio mi/me = 50, relativistic Lorentz factor and cold distributions kBTe/mec2 = 10−4 was performed. The simulation box dimensions were Lx = 4000 c/ωpe and Ly = 320 c/ωpe with resolution , and .