Abstract
Predicting how large an earthquake can be, where and when it will strike remains an elusive goal in spite of the ever-increasing volume of data collected by earth scientists. In this paper, we introduce a universal model of fusion-fission processes that can be used to predict earthquakes starting from catalog data. We show how the equilibrium dynamics of this model very naturally explains the Gutenberg-Richter law. Using the high-resolution earthquake catalog of Taiwan between Jan 1994 and Feb 2009, we illustrate how out-of-equilibrium spatio-temporal signatures in the time interval between earthquakes and the integrated energy released by earthquakes can be used to reliably determine the times, magnitudes and locations of large earthquakes, as well as the maximum numbers of large aftershocks that would follow.
Similar content being viewed by others
Introduction
Urbanization is accelerating in developing countries1, where the primary concern is building fast to meet growing demands for residential and commercial spaces. Many of these new or growing cities are in seismically active parts of the world, thus exposing more and more people to earthquake hazards. This danger is demonstrated clearly in the M-8.0 Wenchuan earthquake on May 12, 2008, where 69,195 people died, 18,392 people went missing2; and the M-7.0 Haiti earthquake on Jan 12, 2010, where 230,000 died3 and 280,000 residential/commercial buildings were destroyed4. It will take a long time before building codes and practices in these countries catch up to those in developed countries like Japan and the United States. Until buildings become earthquake-proof, the biggest difference we as scientists can make for these people may be to predict earthquakes more reliably.
But can earthquakes really be predicted on firm scientific grounds? The prevailing mood now appears to be resignation, i.e. either it cannot be done, or we simply do not understand enough to predict earthquakes in the foreseeable future5,6. To understand why, in the words of Wyss7, “earthquake prediction research is not progressing faster”, let us consider the dichotomy between long-term (decades to centuries) time-independent risk assessment and medium-term (years) time-dependent risk assessment (generally accepted8) and short-term (days to months) probabilistic forecasting and deterministic prediction (always controversial9). As pointed out by Geller10, this distrust of short-term forecasting or prediction stems from the fact that claims of highly convoluted earthquake precursors frequently revolve around the study of one or two anecdotal large earthquakes. In such retrospective studies, it is easy to be lured into ‘tuning’ the precursors to produce apparently significant predictions. Naturally, such precursors cannot be expected to work a second time. A convincing precursor must therefore be structurally simple and testable against easy-to-understand null hypotheses to establish statistical significance.
Clearly, realistic models of earthquake processes will settle the earthquake prediction debate. At present, earthquakes are understood to be the products of interactions between tectonic plates at the largest length scales and longest time scales. However, such macroscopic models of tectonic plates naturally average over earthquakes and hence cannot be used make predictions on them. A generally accepted microscopic model of the highly hierarchical and highly heterogeneous lithospheric earthquake fault system does not exist. Fortunately, the suggestion by Keilis-Borok that the lithosphere is a nonlinear system11,12 both explains why earthquake prediction is so difficult and points out the way to do so without first building a realistic microscopic model. Essentially, in a nonlinear system, linear forcing frequently produces little or no change to the state of the system, until a critical point is reached. At this critical point, the state of the nonlinear system changes abruptly and irreversibly. From this point of view, earthquakes are critical transitions in the state of the lithosphere.
Although they are abrupt, critical transitions fall into a small number of universal classes that do not depend on microscopic details. In a recent series of papers and reviews13,14,15,16,17, Scheffer et al. demonstrated how we could exploit critical slowing down and critical fluctuations to forecast critical transitions. In fact, the pattern informatics approach to earthquake forecasting18,19,20 is related to the coarsening feature that precedes a critical transition. In this paper, we adopt a different approach based on the same principle of universality. As we coarse grain microscopic models near their critical points, we obtain universal mesoscopic models that capture essential features of the physics with fewer parameters.
Universal mesoscopic model
At the mesoscopic level, it is not unreasonable to assume that the fault plane is made up of numerous elements (e.g. asperities) that normally slip past each other21, dissipating the energy of the collisions between tectonic plates (see Figure 1). Sometimes, these elements get stuck, building up large compressive or shear stresses. Decades of research on force networks and jamming in granular media tell us that strong interactions between elements could result in smaller clusters of stressed elements coalescing into larger clusters22,23. When two stressed elements finally slip past each other, the delicate balance of forces within the cluster is destroyed, which then disintegrates very rapidly into the individual elements, releasing the stress energy in the form of an earthquake. Whatever the microscopic model of stress buildup and cascading failure may be, we inevitably end up with a mesoscopic model of fusion and fission processes.
To turn this qualitative picture into quantitative understanding, we make use of the analogy between this network picture and the soup-of-groups (SOG) model developed by Johnson and co-workers24,25 for understanding the size distributions of attacks made by terrorist and insurgent organizations. In this model, members of a terrorist or insurgent organization actively form groups and these groups merge to form larger groups, for the purpose of initiating larger attacks on their adversary. At the same time, such groups are also under the pressure to disband, to avoid detection or limit the effectiveness of pursuit by the police or the army. To demonstrate how such a statistical model of fusion-fission processes can help us predict large earthquakes, let us first show the Gutenberg-Richter law

where F(m > M) is the frequency of earthquakes with magnitudes m larger than a given magnitude M26, very naturally emerges from the equilibrium dynamics of this SOG earthquake model.
We start from the master equations


of the fusion-fission processes. In these equations, nk is the number of clusters with k objects and N is the total number of objects in the SOG system. The two independent parameters in this model are ν+, the coalescence or fusion rate and ν−, the fragmentation or fission rate, assumed to be independent of cluster size. Solving this model, Johnson et al. found a power-law equilibrium size distribution

with a universal exponent α which depends only on the dimensionality d of the model25. For infinite dimensions, which is the case for terrorism or insurgency,  25. For lower dimensions,
25. For lower dimensions,  27. In particular, for a (d = 2)-dimensional SOG model, the exponent is
27. In particular, for a (d = 2)-dimensional SOG model, the exponent is  27.
27.
In the Gutenberg-Richter law, the exponent b is very close to 1. If we rewrite the Gutenberg-Richter law

as a cumulative distribution, where e = 10m and E = 10M are the energy released by magnitude-m and magnitude-M earthquakes respectively, the underlying probability distribution for earthquake energies must be

Therefore, a two-dimensional SOG model where the energy e released by an earthquake is proportional to the size s of a cluster of crustal elements that disintegrated, very naturally explains the Gutenberg-Richter law.
For some time, there was hope that the universal theory of self-organized criticality (SOC) would explain all empirical earthquake laws28, but interest is waning as no success appears to be forthcoming. The greatest difference between the SOC and SOG models is in the latter allowing us to understand out-of-equilibrium dynamics preceding large earthquakes. Within this model, we understand that the SOG cluster of a large earthquake takes time to build up. As the cluster grows in size, the finite SOG system falls out of equilibrium and we have progressive suppression of earthquakes from the largest to the smallest (see Section S1 of SI). The SOG earthquake model therefore predicts fewer smaller earthquakes (quiescence) before a large earthquake, leading to longer and longer time intervals between smaller earthquakes (see Section S2 of SI). This suppression feature also means that the rate at which energy is released by smaller earthquakes become smaller and smaller (see Section S3 of SI). Finally, because the network of asperities lies on a nearly two-dimensional fault plane, the giant SOG cluster must also be spatially localized (see Section S4 of SI). In this paper we discuss how these precursor signatures can be used for forecasting purposes, using the high-resolution Taiwan earthquake catalog between Jan 1994 and Feb 2009 for statistical verification and the 1999 M-7.3 Chi-Chi earthquake as a specific example for illustration purposes.
Results
Time interval SOG signature
In Figure 2, we show the reported time intervals between successive earthquakes for the 1995 M-7.2 Kobe earthquake and the 1999 M-7.3 Chi-Chi earthquake. The expected precursor signature shown in Figure S2 shows up very clearly for these two very large earthquakes. In Section S5 of SI, we also fit the empirical time intervals to the mean field theory, to estimate the average growth rate of the giant clusters, the nucleation time, as well as the time of the largest possible earthquake. Based on the nonlinear fits, we find the Kobe and Chi-Chi SOG clusters growing at fractional rates (relative to the maximum cluster size) of 4.6 × 10−6/day and 1.0 × 10−3/day respectively. This suggests that the Kobe and Chi-Chi earthquakes took 593 years and 2.7 years respectively to build up.
Time interval between successive earthquakes as a function of time, showing SOG signature for two large earthquakes indicated by red vertical lines: (a) Jan 16, 1995 M-7.2 Kobe earthquake and (b) Sep 20, 1999 M-7.3 Chi-Chi earthquake.
These plots are created using earthquake catalogs with earthquakes down to (a) M = 1.5 and (b) M = 0.0.
Integrated energy SOG signature
Although the time interval signature appears universal, it is not sufficiently sensitive for forecasting purposes due to strong fluctuations in the time intervals. The signal-to-noise ratio is not improved even with spatial localization, an aspect of the SOG earthquake model discussed in Section S4 of SI. We therefore focused on making predictions based on the integrated nonlinear energy signature.
In Figure 3(a), we show the integrated nonlinear energy leading up to the Sep 20, 1999 M-7.3 Chi-Chi earthquake. In this figure, the most pronounced feature is the rapid energy release by the Chi-Chi earthquake and its aftershocks. Long before the Chi-Chi earthquake, we also find the linear growth in integrated nonlinear energy expected from the equilibrium SOG model. Just before the Chi-Chi earthquake, this growth in integrated nonlinear energy slows down. When we subtract the empirical integrated nonlinear energy from the fitted mean-field linear growth, we find the nonlinear energy deficit precursor shown in Figure 3(b).
Integrated nonlinear energy released by M < 6.0 earthquakes (a) and deviation from linear growth (b) as a function of time, in the period leading up to the Sep 20, 1999 M-7.3 Chi-Chi earthquake. In (a), the green linear fit was performed on the integrated nonlinear energy between 20 Apr 1997 and 2 Sep 1998 and extrapolated to 15 Jan 2000. The integrated energy deviation shown in (b) is then obtained by subtracting the empirical integrated nonlinear energy from the mean-field linear growth. In both plots, red vertical lines mark M > 6.0 earthquakes. The nonlinear curve fit shown in Section S5 of SI gives us a fractional growth rate of 1.7 × 10−4/day for the Chi-Chi SOG cluster. We believe this estimate is more reliable than the one obtained from a nonlinear curve fit to the time interval SOG signature, which is one order of magnitude larger, even though no meaningful confidence intervals could be extracted from both fits. In (c), we show the integrated energy released by the aftershocks of Chi-Chi as a function of time after the main M-7.3 event.
The final nonlinear energy deficit is two orders of magnitude larger than the nonlinear energy released by the Chi-Chi earthquake, which is only equivalent to 3.7 M-6.0 earthquakes. Therefore, the Chi-Chi earthquake alone could not have accounted for the final nonlinear energy deficit. To properly account for this missing nonlinear energy, we considered all aftershocks of Chi-Chi. Since aftershocks are hard to identify29,30,31, we used the Baiesi and Paczuski method32 to identify 1097 M > 3 earthquakes most correlated to Chi-Chi (for details see Section S6). Adding up the energy released by Chi-Chi and its Baiesi-Paczuski aftershocks, we find from Figure 3(c) that the energy deficit associated with Chi-Chi was recovered after about four months. This suggests that the nonlinear energy deficit is quantitatively meaningful and can be used to roughly forecast the maximum number of aftershocks above a certain size and also when the aftershock sequence will end.
‘Forecasting’ the Chi-Chi earthquake
Finally, we demonstrate the forecasting potential of the integrated nonlinear energy precursor. In Figure 4, we show the nonlinear energy deficits of all cells in the form of a color map, with zero deficits shown in green, moderate deficits shown in yellow and large deficits shown in orange and red. It is clear from Figure 4 that the cluster of cells with positive nonlinear energy deficits is growing with time up till the Chi-Chi earthquake, whose epicenter lies within the SOG cluster. Movie S1 shows how the cellular integrated nonlinear energy signature evolves over the 55 weeks between Sep 1, 1998 and Sep 20, 1999. In Section S7 of SI we show how particular anomalies in the cellular forecasting scheme can be exploited to more precisely forecast the epicenter of the ‘impending’ large earthquake.
SOG energy deficits of cells for week 1 (top left), week 20 (top right), week 40 (bottom left) and week 55 (bottom right).
In this figure, the epicenter of the Sep 1999 Chi-Chi earthquake is marked with a ‘+’. Energy deficits close to zero are green, moderate energy deficits are yellow and large energy deficits are orange and red. In week 55, two of the cells have energy deficits so large that they appear deep red in the plot. The deep blue cells contain too few earthquakes for the energy deficit to be estimated. See Supplementary Section S7 for discussions on the anomalous blue cells within the SOG cluster seen in weeks 20 and 55 and Movie S1 for the entire week-to-week time evolution.
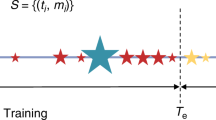
In Figure 5, we illustrate how the timing of the Chi-Chi earthquake can be ‘forecasted’, by fitting the integrated nonlinear energy to its mean-field formula in larger and larger time windows with the same starting time. When the ending time of the fitting window is far from the Chi-Chi earthquake (in the linear growth regime), the event horizon occurs far into the future. When the ending time approaches the Chi-Chi earthquake, the event horizon occurs in between the two times. Finally, once the ending time is within 40 days of the actual earthquake, the event horizon stops changing at a time about a month after the Chi-Chi earthquake. The whole ‘real-time forecasting’ sequence is shown in Movie S2.
Event horizons (dashed cyan vertical lines) obtained from nonlinear curve fits (green curves) of the integrated nonlinear energy SOG signatures (blue curves) of the Sep 1999 Chi-Chi earthquake (solid red vertical lines) (top four panels).
The ending times tend of the fitting window (magenta rectangles) are systematically varied from date number 729960 to 730380 in steps of 10 days. For the nonlinear curve fit, we normalize time such that the start time of the fitting window is set to  while the time of the Sep 1999 Chi-Chi earthquake is set to
while the time of the Sep 1999 Chi-Chi earthquake is set to  .
.
Discussion
In computing the time interval and integrated energy signatures, we included earthquakes with magnitudes down to M = 0.0 for the Taiwan earthquake catalog (and down to M = 1.5 for the Japan earthquake catalog to plot Figure 2(a)). Earth scientists worry about using these small earthquakes for prediction, because many such earthquakes frequently went undetected. Fortunately, both SOG precursor signatures are not sensitive to the completeness of the earthquake catalog at these small magnitudes, provided that the fraction of missing small earthquakes is temporally homogeneous (i.e. same fraction of small earthquakes missed at different times). So long as this is satisfied, we do not even need the missing fraction to be spatially homogeneous (i.e. same fraction of small earthquakes missed in different places) to make plausible predictions. Even though the integrated energy precursor is already visible from the sufficiently many M > 3 earthquakes, we go down to even smaller earthquakes to improve our signal-to-noise level.
In Figure 3(b), we see that up until the Jul 17, 1998 M-6.2 earthquake in Chiayi County, 42 km south of the Sep 20, 1999 M-7.3 Chi-Chi epicenter, the nonlinear energy deficit did not exceed 10 M-6.0 earthquakes. Shortly after the Chiayi earthquake, the nonlinear energy deficit grew consistently, eventually reaching nearly 100 M-6.0 earthquakes before the Chi-Chi earthquake struck. Based on this signature, we can start to tell of an imminent earthquake at the end of Jan 1999. At the end of Jun 1999, the nonlinear energy deficit would have been growing continuously for five months, reaching an equivalent of about 60 M-6.0 earthquakes. If planners could have taken heed at this point, there would still be three months left to make preparations.
From the Chi-Chi case study, we see that the growth of the large SOG cluster can be tracked, for us to estimate the likely epicenter. In particular, Movie S1 very clearly shows two smaller SOG clusters, one along the east coast of Taiwan and the other in the middle of Taiwan, merging into a giant cluster. Shortly after the fusion event, the Chi-Chi earthquake occurred. Geographically, Chi-Chi is close to the focal point between the Ryukyu arc and the Luzon arc, if we extrapolate these inland. This suggests that the fusion event that led to Chi-Chi is the result of interactions between these two tectonic fault systems.
In fact, the anomalies discussed in Section S7 of SI suggests a northward migrating sequence of earthquakes after the Jul 17, 1998 M-6.2 earthquake in Chiayi County: (1) a M-5.51 earthquake on Nov 17, 1998 in Pintung County, (2) a M-5.10 earthquake on Jul 7, 1999 in Chiayi County and then finally (3) the M-7.30 Chi-Chi earthquake on Sep 20, 1999. The line joining these three earthquakes lies close to the extension of the Luzon arc inland into Taiwan.
Thus far we have illustrated the power of the SOG model for earthquake prediction, using the M-7.30 Chi-Chi earthquake as a case study. We have shown how all the expected precursors (increasing time interval between earthquakes, decreasing rate of energy released and spatial localization) consistent with a growing SOG cluster have all been found prior to Chi-Chi. Naturally, a single case study invites skepticism, but we are confident the positive SOG precursor seen for Chi-Chi is not a fluke.
To demonstrate that the SOG earthquake model produces statistically significant precursors, we test the integrated energy precursor systematically for other M > 6 main shocks in Section S8 of SI. In time intervals devoid of large M > 6 earthquakes, we find that for time windows between 10 days and 50 days, the distribution of energy deficits is centered around zero deficit, with a standard deviation not exceeding 20 M-6.0 earthquakes. Using an energy deficit of 20 M-6.0 earthquakes as the cutoff, we find a true positive rate of no less than 5/12 = 0.42 for the 12 M > 6 main shocks tested. At this cutoff, the false positive rate is 234/3468 = 0.067 for a 50-day time window.
In Section S9 of SI, we also tested the time interval signature and integrated energy signature against a synthetic earthquake catalog generated using the spatio-temporal epidemic-type activation sequence (STETAS) model33. None of the M > 6 earthquakes in this synthetic catalog are accompanied by statistically significant precursors. We expect the same null outcome if we had tested the precursors against the Taiwan earthquake catalog reshuffled in space or in time.
From the Chi-Chi case study, we see that an impending large earthquake can be detected as early as several months before. By monitoring the SOG energy deficit shown in Figure 3(b), we can arrive at a rough estimate on the size of the impending earthquake, i.e. small earthquakes are the most likely to occur if the energy deficit is small and a large earthquake is more likely to occur if the energy deficit is large, instead of having the energy released through a series of only small earthquakes.
In itself, the SOG earthquake model does not provide a good prediction on where the epicenter of the impending earthquake will be: it can be anywhere within the giant SOG cluster whose growth can be detected using the cellular precursor map shown in Figure 4. However, anomalies within the giant SOG cluster in the cellular precursor map point to the likely epicenter. Moreover, from a physical point of view it is reasonable to expect the future epicenter to be close to where two smaller clusters merged.
Finally, through fitting the integrated energy signature to its mean field theory in Sections S3 and S5 of SI, we can very accurately determine the event horizon up to several months before the large earthquake. In the Chi-Chi case study, the timing of the earthquake falls within the one-month range within which the event horizon fluctuated. Therefore, even though we cannot predict the large earthquake down to the day, there is still great potential for using this prediction for pre-crisis management and evacuation. In fact, this growing fitting window prediction method can be made automatic and real-time, i.e. as a smaller earthquake is added to the catalog, we can redo the nonlinear fitting to obtain a new event horizon. In this way, at any point in time we always have a most up-to-date prediction of when an earthquake of the largest magnitude can occur.
Methods
Data
For this study we used the high-resolution earthquake catalog of Taiwan from Jan 1973 to Feb 2009. From 1973 to 1993, we are confident that records of earthquakes with M > 3 are complete. After Nov 10, 1993, earthquakes with magnitudes down to M = 0.0 began to appear in the earthquake catalog, but we are only confident that records of earthquakes with M > 2.0 are complete. For our case study and systematic test, we use the catalog starting Jan 1, 1994. In our analysis, we can eliminate earthquake magnitudes that are incomplete in the catalog. We chose not to, because they contain useful information. More importantly, as highlighted in the Discussion section, the SOG precursors are not sensitive to incompleteness in the catalog.
When we systematically examine all 86 M > 6 earthquakes in the Taiwan catalog, we find that it is difficult to extract SOG precursor signatures for most large earthquakes. Because these precursors are developed assuming time-independent SOG equilibrium preceding large earthquakes, they apply only to main shocks. After a main shock, the SOG system is strongly out of equilibrium. Therefore, aftershocks occur as the system is relaxing towards equilibrium. We will need to develop non-equilibrium precursors in order to analyze these in the future. Furthermore, for smaller submarine earthquakes, records are available only when buoys are deployed. Records of such earthquakes are therefore available for disjoint observation periods of the year. Since their records cannot satisfy the uniform incompleteness requirement for our method, we therefore exclude submarine earthquakes from our study.
In this paper, we focus therefore only on main shocks occurring within the Taiwan island after Jan 1, 1994. We first tried identifying these using the Baiesi-Paczuski method described in Section S6 of SI, but this proved to be problematic. Therefore, we selected the set of ‘main shocks’ manually. A M > 6 earthquake is considered a ‘main shock’ if it appears outside of the aftershock feature in the integrated energy. There are a total of 39 such earthquakes. Of the 21 that have no visible slowing down signatures, nearly all are submarine earthquakes. 12 M > 6 earthquakes have visible slowing down signatures and we checked that most of them occurred with the island of Taiwan. Finally, 6 have especially problematic integrated energy signatures that we treat separately. These are described in detail in Section S8 of SI, where we tested the terrestrial and coastal earthquakes for statistical significance.
Time interval between earthquakes
In Section S2 of SI, we explained how the time interval between earthquakes, ignoring their magnitudes, should fluctuate about a mean-field value τ0. When there is a giant SOG cluster growing slowly within the system, this time interval grows with time. To detect this precursor, we subtract the timing ti of earthquake i in the catalog from the timing ti+1 of earthquake i + 1 immediately following it, ignoring both their magnitudes. We then plot the time interval Δti = ti+1 − ti against ti and superimposed onto this graph the timings of the M > 6 earthquakes.
Integrated nonlinear energy
When the SOG system is in equilibrium, we explained using mean-field theory in Section S3 of SI how the integrated energy  will be a linear function E(t) = α(t − t0) of time, with a slope α that depends on the region of interest. Here t0 is our reference date of Jan 1, 1973. When a giant SOG cluster is slowly growing, we expect the rates of increase of E(t) = α(t − t0) − ΔE(t) to become slower, with an energy deficit ΔE(t) ≥ 0 that grows with time. This energy deficit can be found by fitting the initial part of E(t) to a straight line.
will be a linear function E(t) = α(t − t0) of time, with a slope α that depends on the region of interest. Here t0 is our reference date of Jan 1, 1973. When a giant SOG cluster is slowly growing, we expect the rates of increase of E(t) = α(t − t0) − ΔE(t) to become slower, with an energy deficit ΔE(t) ≥ 0 that grows with time. This energy deficit can be found by fitting the initial part of E(t) to a straight line.
However, as explained in Section S3 of SI, this slowing down is less apparent in E(t), because even M = 5.0 earthquakes produce visible jumps in the graph and thus reliable linear fits are difficult to obtain. Since the precursor signature appears in all functions of E(t) within the mean-field limit, we therefore analyzed the integrated nonlinear energy  instead, by plotting the cumulative sum of expmi against ti. The nonlinear energy deficit ΔE′ = α′(t − t0) − E′(t) can then be determined by fitting the initial part of E′(t) to a straight line.
instead, by plotting the cumulative sum of expmi against ti. The nonlinear energy deficit ΔE′ = α′(t − t0) − E′(t) can then be determined by fitting the initial part of E′(t) to a straight line.
Cellular integrated energy forecasting
To predict the epicenter of an impending large earthquake, we look at how the integrated nonlinear energy signature vary in both space and time. To do this for the Chi-Chi earthquake case study, we break the rectangular region bound by the latitudes 22°N and 26°N and the longitudes 119°E and 123°E into 0.5° × 0.5° cells. The size of a cell is decided by a compromise between spatial resolution and having sufficiently many earthquakes in each cell. We then evaluated the nonlinear energy deficit in each cell every week starting from Sep 1998.
Real-time prediction of event horizon
To predict the timing of the impending earthquake, we fit the empirical integrated energy to the deterministic mean field theory in Section S3 of SI, using the procedure outlined in Section S5 of SI. The nonlinear fit gives us the event horizon, which is time of the largest possible earthquake. To mimic conditions of a real-time forecast, we begin with a 460-day window starting Apr 20, 1997 and enlarge it 10 days at a time. We fit only the integrated energy within each time window to the mean field theory, to obtain the associated event horizon. We then compare the slow time evolution of the event horizon against the expected behavior described in Section S10 of SI.
In practice, because of jumps in the empirical integrated energy curve caused by moderate earthquakes, the event horizon fluctuates. If the jump is too large, the nonlinear curve fitting function in MATLAB can give an event horizon before the start of the time window or within the fitting time window. Therefore, during the nonlinear curve fitting we have to restrict the event horizon to occur after the end of the fitting time window.
References
Atkins (2012) Future Proofing Cities. Report available at http://www.futureproofingcities.com/. Accessed September 25, 2013.
Sina.com (July 21, 2008) As of July 21, 69197 perished, 18222 missing in Sichuan earthquake (article in Chinese). URL: http://news.sina.com.cn/c/2008-07-21/170415971186.shtml. Accessed September 25, 2013.
BBC (February 11, 2010) Haiti quake death toll rises to 230,000. URL: http://news.bbc.co.uk/2/hi/americas/8507531.stm. Accessed September 25, 2013.
The Age (February 5, 2010) Haitians angry over slow aid. URL: http://www.theage.com.au/world/haitians-angry-over-slow-aid-20100204-ng2g.html. Accessed September 25, 2013.
Geller, R. J. Earthquake prediction: a critical review. Geophys. J. Int. 131, 425–450 (1997).
Geller, R. J., Jackson, D. D., Kagan, Y. Y. & Mulargia, F. Enhanced: earthquakes cannot be predicted. Science 275, 1616–1620 (1997).
Wyss, M. Why is earthquake prediction research not progressing faster? Tectonophysics 338, 217–223 (2001).
Jordan, T. H. & Jones, L. M. Operational earthquake forecasting: some thoughts on why and how. Seismol. Res. Lett. 81, 571–574 (2010).
Main, I. Is the reliable prediction of individual earthquakes a realistic scientific goal? Nature 397(1), (1999).
Geller, R. J. Earthquake prediction: is this debate necessary? Nature 397(1), (1999).
Keilis-Borok, V. I. The lithosphere of the Earth as a nonlinear system with implications for earthquake prediction. Rev. Geophys. 28, 19–34 (1990).
Keilis-Borok, V. I. Earthquake prediction: state-of-the-art and emerging possibilities. Annu. Rev. Earth Pl. Sc. 30, 1–33 (2002).
Scheffer, M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009).
Hirota, M., Holmgren, M., van Nes, E. H. & Scheffer, M. Global resilience of tropical forest and savanna to critical transitions. Science 334, 232–235 (2011).
Veraart, A. J. et al. Recovery rates reflect distance to a tipping point in a living system. Nature 481, 357–360 (2012).
Scheffer, M., Hirota, M., Holmgren, M., van Nes, E. H. & Chapin, F. S. Thresholds for boreal biome transitions. Proc. Natl. Acad. Sci. USA 109, 21384–21389 (2012).
Scheffer, M. et al. Anticipating critical transitions. Science 338, 344–348 (2012).
Rundle, J. B., Tiampo, K. F., Klein, W. & Martins, J. S. S. Self-organization in leaky threshold systems: The influence of near mean field dynamics and its implications for earthquakes, neurobiology and forecasting. Proc. Natl. Acad. Sci. USA 99, 2514–2521 (2002).
Tiampo, K. F., Rundle, J. B., McGinnis, S., Gross, S. J. & Klein, W. Mean-field threshold systems and phase dynamics: An application to earthquake fault systems. Europhys. Lett. 60, 481–487 (2002).
Rundle, J. B., Turcotte, D. L., Shcherbakov, R., Klein, W. & Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 41(4), 1019 (2003).
Aki, K. Higher-order interrelations between seismogenic structures and earthquake processes. Tectonophysics 211, 1–12 (1992).
Luding, S. & Hermann, H. J. Cluster-growth in freely cooling granular media. Chaos 9, 673–681 (1999).
Aranson, I. S. et al. Electrostatically driven granular media: phase transitions and coarsening. Phys. Rev. Lett. 84, 3306–3309 (2000).
Bohorquez, J. C., Gourley, S., Dixon, A. R., Spagat, M. & Johnson, N. F. Common ecology quantifies human insurgency. Nature 462, 911–914 (2009).
Johnson, N. F., Ashkenazi, J., Zhao, Z. & Quiroga, L. Equivalent dynamical complexity in a many-body quantum and collective human system. AIP Adv. 1, 012114 (2011).
Gutenberg, B. & Richter, C. F. Frequency of earthquakes in California. B. Seismol. Soc. Am. 34(4), 185–188 (1944).
Stauffer, D. & Aharony, A. Introduction to Percolation Theory (Taylor and Francis, London) (1994).
Turcotte, D. L. Self-organized criticality. Rep. Prog. Phys. 62(10), 1377–1429 (1999).
Davis, S. D. & Frohlich, C. Single-link cluster analysis, synthetic earthquake catalogues and aftershock identification. Geophys. J. Int. 104, 289–306 (1991).
Molchan, G. M. & Dmitrieva, O. E. Aftershock identification: methods and new approaches. Geophys. J. Int. 109, 501–516 (1992).
Bottiglieri, M., Lippiello, E., Godano, C. & de Arcangelis, L. Identification and spatiotemporal organization of aftershocks. J. Geophys. Res. 114, B03303 (2009).
Baiesi, M. & Paczuski, M. Scale-free networks of earthquakes and aftershocks. Phys. Rev. E 69, 066106 (2004).
Ogata, Y. Space-time point-process models for earthquake occurrences. Ann. I. Stat. Math. 50, 379–402 (1998).
Acknowledgements
P.M.A.S. acknowledges a grant from the ‘‘Leading Scientist Program’’ of the Government of the Russian Federation, under contract 11.G34.31.0019. P.M.A.S. also acknowledges the support from the FET-Proactive grant TOPDRIM, number FP7-ICT-318121.
Author information
Authors and Affiliations
Contributions
S.A.C., C.C.C., W.L.C., L.Y.C., P.M.A.S. and N.F.J. conceived the study. C.C.C. and W.L.C. contributed the data. S.A.C., T.L.T. and Z.L. performed the data analyses. S.A.C. wrote the manuscript and supplementary text. S.A.C. and T.L.T. prepared the figures in the manuscript and supplementary text. All authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
SI Short-Term Forecasting of Taiwanese Earthquakes Using a Universal Model of Fusion-Fission Processes
Supplementary Information
Weekly cellular plots with Taiwan outline
Supplementary Information
Event Horizon of the Chi-Chi earthquake
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Cheong, S., Tan, T., Chen, CC. et al. Short-Term Forecasting of Taiwanese Earthquakes Using a Universal Model of Fusion-Fission Processes. Sci Rep 4, 3624 (2014). https://doi.org/10.1038/srep03624
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep03624
This article is cited by
-
Pattern Informatics and the Soup-of-Groups Model of Earthquakes: A Case Study of Italian Seismicity
Pure and Applied Geophysics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.