Introduction

Graphene is a zero gap semiconductor with very weak spin-orbit coupling (SOC)1. Since its discovery a lot of efforts have been undertaken to engineer a finite band gap, but no satisfactory progress could be achieved. Silicene is closely related to graphene, as they share the same two-dimensional honeycomb structure and has been proposed as a potential candidate for overcoming the limitations of graphene due to its buckled structure and much stronger SOC. Silicene has first been reported by Takeda and Shiraishi2 and investigated in more detail in Ref. 3. While C and Si belong to the same group in the periodic table, Si has a larger ionic radius, which promotes sp3 hybridization. The mixture of sp2 and sp3 hybridization in silicene results in a prominent buckling of 0.46 Å, which can open an electrically tunable band gap4,5. On the other hand, the band gap induced by the intrinsic SOC was found to amount to 1.6 meV6. First principles calculations have confirmed that the stable structure of silicene is buckled7. Similar to graphene, the charge carriers in silicene are expected to behave like massless Dirac fermions in the π and π* bands, which form a Dirac cone at the K-point. The electronic properties of halogenated and hydrogenated silicene have been studied by first principles calculations in Refs. 8, 9 and the effects of different substrates on the Dirac cone have been analyzed in Refs. 10,11,12.

Growth of silicene and its derivatives experimentally has been demonstrated for different metal substrates13,14,15. Silicene on a ZrB2 thin film shows an asymmetric buckling due to the interaction with the substrate, which leads to the opening of a band gap. However, accurate measurements of the materials properties are difficult on metallic substrates. In addition, metallic substrates screen externally applied electric fields and therefore prohibit manipulation of the electronic structure. For this reason, it would be desirable to achieve free-standing silicene. However, free-standing silicene probably is instable against a transition into the silicon structure. A possible solution can be a superlattice that stabilizes the two-dimensional structure of silicene but still is characterized by a small interaction to the second component so that the Dirac states are not perturbed. In the following we will substantiate this idea by first principles calculations. Due to an identical honeycomb structure, the superlattice of silicene and hexagonal boron nitride appears to be a promising choice. In addition, hexagonal boron nitride is a wide band gap semiconductor and therefore makes it possible to study the effects of an external perpendicular electric field applied to silicene. Because of the remarkably buckled structure, the intrinsic SOC gap of silicene can be enhanced by a perpendicular external electric field. Hence, we will study the electronic structure of silicene under an electric field Ez using band structure calculations as well as an analytical model.

Results

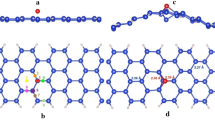
The structural arrangement of the superlattice under study is depicted in Fig. 1, showing silicene and hexagonal boron nitride layers that alternate along the z-axis. We have also studied superlattices with hexagonal boron nitride slabs of varying thickness. However, since it turns out that this thickness has hardly any influence on the silicene electronic states, in particular the charge transfer between the two component materials, we will focus in the following on the case of one layer of hexagonal boron nitride alternating with one layer of silicene. Our structural optimization results in a Si–Si bond length of 2.26 Å and a buckling of 0.54 Å in the silicene layer. The latter value is slightly but not significantly higher than the predicted value of free-standing silicene6,16. The bond angle between neighboring Si atoms amounts to 114°, which agrees well with the value of 116° in free-standing silicene. For the interlayer distance between the silicene and hexagonal boron nitride layers we obtain a value of 3.35 Å, resembling the distance of a silicene layer from a h-BN substrate10,11.

Figure 1
figure 1

Superlattice of silicene (top) and hexagonal boron nitride (bottom) viewed along the hexagonal b-axis.

Full size image

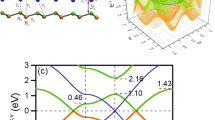
The presence of a Dirac cone has been claimed for silicene grown on metallic substrate but there is still an ongoing discussion about the validity of this claim13,14,15,17. Because of the large band gap of hexagonal boron nitride, we do not expect B or N states in the vicinity of the Fermi level in the case of our superlattice, so that the situation is much less involved. The band structure obtained from our calculations is shown in Fig. 2. We observe indeed a well preserved Dirac cone with a SOC gap of 1.6 meV. Analysis of the partial densities of states (not shown) clearly demonstrates that the Dirac cone traces back to the pz orbitals of the Si atoms, while contributions of the B and N atoms are found above 0.6 eV and below −1.0 eV only, with respect to the Fermi energy. We note that the observed Dirac cone is slightly shifted such that the Dirac point does not fall exactly on the Fermi energy. It appears at an energy of about 0.04 eV, i.e., the silicene is slightly hole doped. The energetical shift of the Dirac cone can be attributed to a tiny charge transfer between the silicene and the hexagonal boron nitride. Quantitative analysis shows that the silicene layer loses 0.06 electrons per 8 atoms. However, besides this small effect (which can be overcome by a minute doping), the charactersitics of the silicene Dirac cone are perfectly maintained in a superlattice with hexagonal boron nitride. In the following we will therefore study the effect of an external electric field on free-standing silicene to describe the properties of the superlattice. In Ref. 4 the role of the intrinsic SOC and external electric field for the opening of a band gap have been discussed. The electric field breaks the sublattice symmetry, which induces a finite band gap. The intrinsic SOC has the same effect. Our calculations (for an ideal buckling of 0.46 Å) show that the SOC (Ez = 0) on its own results in a band gap of 1.6 meV, which is consistent with the previously reported value in Ref. 4. To obtain the same gap by an electric field (without SOC) a value of Ez = 11.2 meV/Å is needed, see Fig. 3(a).

Figure 2
figure 2

Electronic band structure obtained for the superlattice of silicene and hexagonal boron nitride.

Full size image
Figure 3
figure 3

Electronic band structure of free-standing silicene: (a) with SOC and Ez = 0 or without SOC and Ez = 0.0112 V/Å, (b–d) with SOC and different values of Ez ≠ 0.

Full size image

From an application point of view, the combined effect of SOC and electric field is of great interest. We therefore vary Ez relative to the fixed SOC. Band structures obtained for three different values of the electric field are shown in Figs. 3(b) to (d). For Ez = 3.1 meV/Å, see Fig. 3(b), we find energy gaps of 1.3 and 7 meV between the minority and majority spin bands, respectively. When we increase Ez to 3.6 meV/Å the obtained energy gaps change to 1.1 and 9 meV, which we will explain later by our analytical model. A stronger electric field of Ez = 11.2 meV/Å leads to energy gaps of 2.9 and 20 meV. Further enhancement of the electric field results in a almost linear increase of the energy gaps. The observed dependence of the energy gaps on the electric field is much stronger than reported previously4,5, because we take into account the SOC. Our results show that there is no spin degeneracy and a finite band gap, which is a combined response of SOC and electric field. In addition, Figs. 3(b) to (d) demonstrate phase transitions from a metal to a topological insulator and further to a band insulator. The electric field required to obtain a reasonable band gap is found to be much smaller than typical fields considered before, which means that the device can be operated in a stable regime at low voltage.

In order to discuss the mechanisms behind the above observations, we consider an analytical model. We assume a silicene sheet lying in the xy-plane in the presence of intrinsic SOC and an external electric field in z-direction. According to the previous findings of our first principles calculations, the effect of the proximity to hexagonal boron nitride can be neglected. Silicene can be described by the two-dimensional Dirac-like Hamiltonian

where η = +1/−1 denotes the K/K′ valley, s = +1/−1 denotes spin up/down, Δ = 2lEz with l = 0.23 Å is the onsite energy difference due to the electric field, (σx, σy, σz) is the vector of Pauli matrices, λ is the strength of the intrinsic SOC and v is the Fermi velocity of the Dirac fermions. For the K valley we have

and for the K′ valley

To obtain the eigenenergies, we diagonalize the Hamiltonian and obtain

where n = +1/−1 denotes the electron/hole band and k is the absolute value of the wave vector. We next discuss the energy eigenvalues obtained for the K point to explore the band splitting and quantum phase transitions. The energy gap of 1.6 meV seen in Fig. 3(a) as obtained for finite SOC or Ez is consistent with Eq. (4), confirming an insulating state. Figure 3(b) for finite SOC and Ez with λ > Δ = 1.4 meV shows an energy splitting between the spin up and spin down bands for both the electrons and holes. This splitting is less than the energy gap between the electrons and holes themselves. In addition, the energy gap between the spin up bands is greater than that between the spin down bands. This situation reflects a topological insulating state, which corresponds to the spin polarization regime. Figure 3(c) is analogous to Fig. 3(b) but for λ ~ Δ = 1.6 meV. We see that the energy gap closes between the spin down bands, while the spin up bands maintain a finite energy gap. In the first principles calculations we cannot reach an exact closure of the spin down gap as suggested by Eq. (4) but obtain a minimum of about 1.1 meV, because of the approximations involved in the simulations. Figure 3(d) is analogous to Figs. 3(b) and (c) but for λ < Δ = 5.1 meV. The splitting of the spin down bands has increased as compared to Fig. 3(b), but less than the splitting of the spin up bands. This situation reflects a band insulator, which corresponds to the valley polarization regime. We note that we obtain an identical band structure for the K′ point with the spin up and spin down bands exchanged. The K and K′ valleys are non-degenerate due to the broken inversion symmetry (which is a consequence of the external electric field and the buckling), compare Eq. (4).

Discussion

In conclusion, we have discussed the structure and electronic properties of a superlattice of silicene and hexagonal boron nitride. We find that the Dirac cone of free-standing silicene remains intact in the superlattice due to a small interaction (the binding energy amounts to only 57 meV per atom). A small amount of charge transfer between the silicene and hexagonal boron nitride results in a slight shift of the Dirac cone towards higher energy, i.e., in slight hole doping. Using an analytical model we have analyzed the combined effects of the intrinsic SOC and an external electric field applied perpendicular to the superlattice. Our results show that a lifting of the spin and valley degeneracies can be achieved. With increasing strength of the electric field, the nature of the system changes from a semimetal to a topological insulator and further to a band insulator. Therefore, control of the quantum phase transitions in silicene is possible by tuning the external electric field.

Methods

Our calculations are carried out using density functional theory in the generalized gradient approximation. Specifically, we employ the Quantum-ESPRESSO package18. The van der Waals interaction19,20 as well as the SOC are taken into account. A finite electric field is applied using the scheme described in Refs. 21, 22. The calculations are performed with a plane wave cutoff energy of 816 eV. Furthermore, a Monkhorst-Pack 8 × 8 × 1 k-mesh is employed for optimizing the crystal structure and a refined 30 × 30 × 1 k-mesh is used afterwards to increase the accuracy of the self-consistency calculation. The supercell employed in our superlattice calculations comprises one layer of hexagonal boron nitride (18 atoms in a 3 × 3 arrangement) and one layer of silicene (8 atoms in a 2 × 2 arrangement). The resulting lattice mismatch is small (2.8%) and comparable to that of the frequently studied superlattice between graphene and hexagonal boron nitride20,23,24,25. We have fully relaxed the structure of the superlattice, finding values of a = b = 7.56 Å and c = 7.77 Å. An energy convergence of 10−8 eV and a force convergence of 4 · 10−4 eV/Å are achieved.