Introduction

Transfer from evanescent wave into propagating wave is an interesting optical problem1, which is still relatively unexplored perhaps because of the distinct feature of evanescent wave. Evanescent wave appears along with moving electrons, and it does not carry power unless electrons are moving faster than light in a medium, which is known as Čerenkov radiation. Čerenkov radiation occurs when fast motion of electrons leaves their accompanying evanescent fields lagged behind in space, which will coherently accumulate into energetic radiation, similar to the sonic boom created by an object travelling faster than sound. A different type of radiation called transition radiation is able to bypass the requirement of fast velocity for electrons, which occurs as long as electrons move through an inhomogeneous media, such as a boundary between two different materials. It is worth mentioning here that Čerenkov radiation from photonic crystals2 is a special case because in photonic crystal, the loss of translational invariance will allow emission of radiation without any threshold velocity of electrons, which has intrinsically coupled with transition radiation.

A third type of radiation also transforming evanescent wave into radiation from electrons' motion is known as diffraction radiation, for which electrons generate radiation in passage near a structured surface without penetrating it. This mechanism has been shown recently in a metamaterial-based structure, which is driven by a free electron beam bunch3. In this light-well source, free electrons interact with periodically-alternating environment as they travel through tunnels inside, and it is proved theoretically that the radiation is due to the diffraction radiation4, which shows a continuum of radiation over a broad angular range. This transfer from kinetic energy of an electron bunch to radiation also bears resemblance to the transition radiation because electrons also interact with inhomogeneous dielectric parameters during their passage. This proof-of-concept not only opens up new type of electron-induced radiation sources, but also inspires one to ponder whether other inhomogeneous structure can induce similar radiation phenomenon.

The recently-developed field of transformation optics5,6 provides the capability to manipulate light flow almost arbitrarily, for instance to hide objects inside a cloak device made of inhomogeneous and anisotropic permittivity and permeability. The invariant form of Maxwell's equations, under various coordinates (including even non-Euclidean systems), allows light to be shaped by curved electromagnetic space in order to design novel devices for various applications. From the perspective of an electron, it does not bend the trajectory similarly to light and instead experience a curved space to induce radiation7. Therefore such a curved electromagnetic space becomes an energy-pumping candidate to give rise to electron's motion-induced radiation in higher frequency with assist of nanofabrication technology8,9. In particular, Zhang et al. invented a method to detect cloak by observing radiation of a fast-moving electron bunch going through the cloak device7. In this paper, we are interested to study the electron's motion-induced radiation for electron bunches moving through a different structure known as Maxwell's fish-eye, which in principle will provide unlimited resolution as a perfect imaging lens10. From our calculation, we will show that the the radiation is a combination of both Čerenkov radiation and transition radiation.

The rest of this paper is structured as follows. For Results section, in Subsection A the basic equations of electromagnetic fields due to moving charges are posed and the analytic solutions to electromagnetic fields are derived by dyadic Green's function. In Subsection B main calculation results are shown including electric fields on xz plane (where electron's trajectory is confined) and field radiation patterns at a frequency of 300 THz. In Discussion Section, we analyze and discuss temporal evolution of electron's radiation from Maxwell's fisheye sphere and then summarize this report with some outlook to the potential application of this work. The formulation of dyadic Green's function method is reported in Method Section and Supplementary information.

Results

A. Question of radiation from the Maxwell's fisheye sphere

In this section we shall pose our problem and try to give some qualitative prediction from the perspective of transformed uniform space. The Maxwell's fisheye lens of refractive index profile

invented by Maxwell himself, focuses light-rays emitted from a source point to its image point antipodally. In this manuscript, we investigate two cases of Maxwell fisheye profile: one is a nonmagnetic Maxwell fisheye sphere, whose permittivity and permeability functions are defined as

For outer space of the Maxwell's fisheye sphere, simply vacuum permittivity is adopted and the whole space we investigate is un-magnetic in order to facilitate possible future experimental work. The other is the impedance-matched full Maxwell fisheye, . As the surface of a sphere is a curved space (with constant curvature), the fish eye profile n(r) can be mapped onto the surface of a hypersphere (4D manifold) in virtual uniform space from Lunburg's visualization11. For simplicity, suppose we generate a pulse of electron beam moving along a straight line in the z-direction inside a Maxwell's fisheye sphere,

Our goal is to obtain the solution to inhomogeneous wave equations of electromagnetic fields from dyadic Green's function method analytically12,13,14. In this manuscript, we take q = 1000e, R1 = 2 μm, x0 = 1 μm, y0 = 0, σ = 50 nm, v = 0.9c (we use 1000 electrons to represent an electron bunch, e indicates elementary charge and c light velocity in vacuum). The formulation of the dyadic Green function to solve Maxwell's equations shall be demonstrated in Methods section. Only dyadic Green function in the source region (the nonmagnetic Maxwell's fisheye sphere) is given here:

in which k is the wavevector, , , , are the eigen-wave vectors in the Maxwell's fisheye sphere, Cmn the coefficient for the infinite series. Thus electric field in in the Maxwell's fisheye sphere can be written as

The Green function for electromagnetic fields in the impedance-matched full Maxwell fisheye has been solved recently15,16. The Green tensor for electric field should be,

in which r and r0 are taken in the relative unit of inner sphere radius R1 and light speed c = 1 to avoid unnecessary factors (See Supplementary information III for its explicit form), however one requires to convert the unit after obtaining the physical quantities. Thus electric field in the impedance-matched Maxwell's fisheye can be written the same as equation (7).

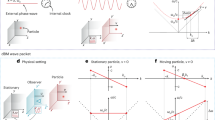
Before any further calculation, it is suggestive to analyze how this curved geometry manipulates different dynamics of light and electron both in physical space and virtual uniform space. In panel (a) of Fig. 1, permittivity distribution on xz plane is demonstrated in bluecolor. According to Hamilton's equations and , in which indicates momentum, ω the Hamiltonian6,17, the light trajectory in xz plane can be traced to follow an arc of a circle within Maxwell's fisheye in green curve, in physical space in panel (a) of Fig. 1; whereas motion of charge does not bend its trajectory at all in dashed magenta line according to our predetermined current density function (5). Now we transform physical space to virtual uniform space to contrast the dynamics of light and charge. Since it is generally difficult to plot surface of a 4-dimensional hypersphere from our human perspective, we reduce this to a simpler counterpart without losing its curved property: surface of a 3-dimensional sphere (panel (b) of Fig. 1) and limit our view to the cross section in xz plane. Mapped to uniform space, light follows geodesics (the green curve) on the lower half (corresponding to interior Maxwell's fisheye) spherical surface. However, the electrons deviate their trajectory from geodesics of spherical surface in uniform space if we transform their trajectory to uniform space (X, Z, Y) from physical space (x, z), according to inverse stereographic projection6 (we change sequence of Y and Z to accommodate xz plane in physical space),

In uniform space, electrons propagate along a curve on lower half spherical surface, shown in dashed magenta circle in Fig. 1(b). From the bent trajectory of charge in virtual uniform space, we can explain why electrons radiate in our question. In this stretched uniform space, electrons actually experience a curved path on lower spherical sphere. This predicts that the electrons will generate a synchrotron radiation within Maxwell's fisheye sphere, in agreement with our results below.

Figure 1: Physical space (upper panel (a)) can be transformed into virtual space lower panel (b) which is curved space under inverse stereographic projection.
figure 1

In both panels green lines indicate the light trajectory while the magenta the electron's trajectory. Panel (a) is the physical space of xz plane with permittivity distribution marked in blue-color, which can be divided into two parts demarcated by the black circle: inner part 0 ≤ r ≤ R1 is Maxwell's fisheye and outer part r > R1 is uniform space (). In colorbar, brighter color indicates the higher value of permittivity. The magenta line indicates the trajectory of electron bunch along straight line x = R1/2, y = 0, z = 0. Panel (b) is the virtual uniform space, composed of two parts corresponding to physical space. One is invariant planar space marked in light blue, ; the other lower half spherical surface in uniform space in pink (mapped from Maxwell's fisheye sphere on xz plane zone, shown in panel (a), according to inverse stereographic projection). Note: green and magenta curve intersects at point x = 1/2, , y = 0. This is solely coincidence due to the parameters we choose.

Full size image

Notice this geometric picture of electron moving on a sphere applies exactly only under the condition of impedance-match, . While the nonmagnetic case, , within Maxwell's fisheye, is derived under the eikonal approximation which allows one to vary permittivity and permeability so that refractive index maintains unchanged18, however at the price of varying the wavefront of electromagnetic fields to a certain extent (this 3D case could not guarantee a trick to keep the polarization under eikonal approximation instead of the 2D case in Ref. 10). Therefore the geometric picture in 1(b) is only an approximation under this nonmagnetic rescaling in equations (2) and (3). However, we shall demonstrate in the next subsection, that the two cases both induce a combination of Čerenkov radiation and transition radiation, and thus our approximation remains valid with regard to the perspective of radiation.

B. Main results

First to demonstrate the unique electromagnetic geometry of Maxwell's fisheye structure, we position an infinitesimal Hertzian electric dipole (l the dipole length)14 at the middle point of the current line, x = R1/2 = 1 μm, y = 0, z = 0, indicated by a black arrow in Fig. 2. In Fig. 2, z component of electric field on plane y = 0 is plotted for single frequency 300 THz (λ = 1 μm). Inside Maxwell's fisheye sphere in Fig. 2(a), light generates from dipole point and follows a curved path which becomes denser in inner part than in outer (while the counterpart for impedance-matched case is plotted in Fig. S1(a) of Supplementary information III, a similar pattern to Fig. 2(a)). This can be explained by the fact that permittivity (or equivalently refractive index) gradually reaches higher in inner part than in outer (also c.f. Fig. S1(a)) to observe similar phenomenon for impedance-matched Maxwell's fisheye). The dashed line in white indicates the discontinuity at circle r = r′, which is due to the piecewise form of dyadic Green function itself in equation (6). Outside the Fisheye, electric field distribution in Fig. 2(a) becomes curvilinear smooth contours, different from scattered contours in (b) (permittivity is uniformly distributed inside the blue circle for a contrast). The smooth contours which squeeze inside fisheye implies that the profile of Maxwell's fisheye could in principle be used to design light absorber.

Figure 2: Electric fields in z direction, Ez(x, z) on xz plane from Hertzian dipole at point x = R1/2 = 1 μm, y = 0, z = 0 (marked as a small black circle) for (a) nonmagnetic Maxwell's fisheye sphere (c.f. also Fig. S1(a) for impedance matched case) and (b) uniform sphere ().
figure 2

The huge-value points along blue circle in (a) are thought to be numerical defect of hypergeometric function. The dashed lines in white in (a–b) indicate where some discontinuity at circle r = r′ is due to piecewise form of dyadic Green function itself in equation (6).

Full size image

Second, we present the magnitude of electric field on xz plane with time. In Figs. 3 (nonmagnetic case) and 4 (impedancematched case) respectively, we present 6 snapshots of magnitudes of the electric field resulting from electron's motion into Maxwell's fisheye sphere. Green left arrows indicate the position of moving electrons, which are moved by distance of 0.5 μm to the right of their actual positions to avoid shading radiation. We define our time scale coordinate so that electrons pass the middle point x = 1 μm, y = z = 0 at time t = 0.

Figure 3: Six snapshots of temporal electric field magnitudes |E(y = 0, x, z, t)| on xz plane for motion-induced radiation from Maxwell's fisheye sphere (nonmagnetic case).
figure 3

Dashed pink lines indicate the trajectory of electrons. Green left arrows indicate the positions of electrons, which are moved by distance of 0.5 μm to the right of their actual positions to avoid shading. We define our time scale coordinate so that electrons pass middle point x = 1 μm, y = z = 0 at time t = 0. Parameters: R1 = 2 μm, q = 1000e, v = 0.9c.

Full size image
Figure 4: Six snapshots of temporal electric field magnitudes |E(y = 0, x, z, t)| on xz plane for motion-induced radiation from Maxwell's fisheye sphere (impedance matched case).
figure 4

Also see the gif file in Supplementary information for transient effect. All the parameters and figure configuration is the same as Fig. 3.

Full size image

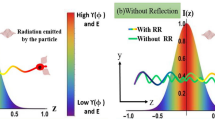
We first analyze nonmagnetic Maxwell fisheye sphere case in Fig. 3. Electrons generate transition radiation as they enter the Maxwell's fisheye sphere (in Fig. 3(a), only the radiation accompanying electrons are real radiation and other spots in front of them are considered as evanescent waves) because they see different medium upon boundary of fisheye. During the whole process when electrons traverse the inner Maxwell's fisheye, because permittivity varies from low to high and low again along the electron path, transition radiation is generated continuously but not uniformly in time due to inhomogeneous permittivity experienced. We observe stronger radiation mainly from the middle part ((b–d) in Fig. 3) of the trajectory within fisheye. In physical space, permittivity distribution along the electron path in the fisheye informs us the maximum permittivity gradient lies near fisheye's boundary (c.f. red curve in Fig. 5), which would suggest stronger transition radiation near the boundary instead. However, this disagrees with our calculation results, which can be explained from the perspective of Čerenkov radiation. In dominant part of electron's path inside the inner sphere, permittivity is greater than (c/v)2( = 1.23) (c.f. light blue curve in Fig. 5), therefore Čerenkov radiation contributes its power and makes the radiation stronger especially in middle part with higher permittivity. This higher permittivity in middle part could also explain why radiation pulse slows down compared with the electrons during time t = 0 ~ 1 fs since light speed slows in high permittivity region. As electrons move out of the fisheye, transition radiation bounces back leftward (Fig. 3(e–f)). And there is, however radiation leftover inside fisheye, although electrons are then absent.

Figure 5: For Maxwell fisheye in nonmagnetic and impedance-matched cases, permittivity function and its derivative function of z coordinate along charge trajectory (x = 1 μm, y = 0, ) investigated.
figure 5

The two arrows indicate the two points where Čerenkov radiation starts and stops, i.e. n(r) = c/v. The interval where Čerenkov radiation lasts is colored lighter in permittivity function lines.

Full size image

The analyse of impedance-matched full Maxwell fisheye in Fig. 4 is similar but not identical. Stronger radiation is also mainly observed in the middle part (panels (b–d) of Fig. 4), because Čerenkov radiation (c.f. light orange curve in Fig. 5) also overweighs and make the whole radiation stronger in the middle part by its higher refractive index (notice that in impedance-matched case, refractive index ). Transition radiation also occurs since the refractive index is continuously varying along the electrons' path in physical space. However, a unique feature of the radiation from impedance-matched Maxwell fisheye is, the electric field accompanying electrons (we call it Electron's Spot (ES) for shortness) carries front and back lobes generally, which switch from the front to the back with time (c.f. (a), (c) and (e) in Fig. 4). In front of or behind field spots, there are other weaker field spots which resembles in shape with ES, except containing a hole in its interior. This type of weak spot keeps rotating away to the left side of electrons' trajectory until it rotates back to align with the electrons' position, when the electrons fill the hole of the weak spot to emanate real radiation from their motion (c.f. gif file in Supplementary information). No scattering light is observed in this case when the electrons move out the the boundary of R1 because impedance-match condition remains valid along this spherical boundary.

We may understand the transition radiation in impedance-matched Maxwell fisheye from perspective of virtual space. In virtual space in panel (b) of Fig. 1, electrons move along the magenta circle on spherical surface, which is equivalent to a synchrotron radiation from accelerated electrons in uniform medium. This acceleration includes both bending trajectory and varying velocity. Since electrons move at a fixed speed in physical space, they move at varying speed along a curved path in virtual space. The radiation thus is a synchrotron radiation nonuniform in time.

Radiation patterns of near and far field corresponding to a single frequency 300 THz of the whole frequency band, are demonstrated for both sets of the parameters investigated. For nonmagnetic case in Fig. 6, the two side lobes spread symmetrically in y coordinate and the two radiation patterns are both pointing outwards. While for impedance-matched case in Fig. 7, the patterns are distinctly different—the near field one carries a radiation power pointing inwards (minus valued) along the minus-x direction and less side lobes are observed. This negative power flow of radiation can be explained by the rotational motion of the weak field spot with a hole by indicating that more power of radiation flows inward than outward at the minus x side of the boundary r = R1. All four radiation patterns demonstrate that the main lobe of radiation is pointed toward motion direction of electrons, z direction and maintains a symmetrical feature along y coordinate as well as a biased broken symmetry along x coordinate. We attribute this bias of pattern to broken symmetry from biased position of injected electron bunch, given by equation (5).

Figure 6: (a) Near field and (b) far field radiation patterns at 300 THz from moving charged particle through nonmagnetic Maxwell's fisheye sphere.
figure 6

Enclosing sphere of calculation is double size of fisheye radius 2R1 = 4 μm and 20R1 = 40 μm. Contours of radiation pattern on xy plane are projected onto ground plane to show asymmetry in x coordinates due to the broken symmetry of injection position.

Full size image
Figure 7: (a) Near field and (b) far field radiation patterns at 300 THz from moving charged particle through the full Maxwell's fisheye for impedance-matched case.
figure 7

Enclosing sphere of calculation is double size of fisheye radius R1 = 2 μm and 20R1 = 40 μm. Other configurations of the figure are the same as Fig. 6.

Full size image

Discussion

From Figs. 2 and S1(a), Maxwell's fisheye structure (of inhomogeneous refractive indices) manipulates light to transit smoothly from uniform space into curved space instead of just scattering the light with uniform permittivity. The different radiation patterns of two kinds of Maxwell fisheye medium, also inspires one to wonder other possible radiation patterns due to other possible but more complicated curved geometry of light.

However, solely from electron's circular trajectory on the lower half sphere in virtual uniform space for impedance-matched Maxwell fisheye profile, we are able to see how electrons perceive this curvature of EM space thus radiate transition radiation. Therefore the radiation from otherwise curved space will bend the electron's trajectory in uniform space to be along other curves (instead of spherical circles), and radiation pattern could contain even more side-lobes. This observation inspires one to engineer certain radiation patterns by varying permittivity and permeability in space and even add in anisotropicity similar to engineering directional beam in19,20.

Remark: In this manuscript material dispersion is not considered for the simplicity of Green function because the emphasis is put on the spatial profile of refractive index which dominantly shapes the electromagnetic wave. Any imposed dispersion relation of and μ(r, ω) could further complicate the derivation of the relevant Green function. Thus this calculation is only valid within a narrow frequency band where our parameter profile applies.

In conclusion, this manuscript investigates radiation from electron's motion through a curved space–Maxwell's fisheye profile. We calculate radiation from Maxwell's fisheye profile (both nonmagnetic and impedance-matched cases) using Green's function method, and finds that it combines both Čerenkov radiation and transition radiation. For the impedance-matched Maxwell's fisheye, we also compare physical space and virtual uniform space to explain the reason electron's motion induces radiation in such a curved space geometry. Our calculation may point to novel methods to manufacture light source pumped from electron's kinetic energy. We also believe it is useful to explore possible radiation characteristics (radiation pattern) from the perspective of engineering permittivity and permeability. It is worth mentioning that electron-induced surface plasmon is also possible to occur when swift electrons interact with metal structure21. This is out of scope of this manuscript, but also shares physics of transfer from evanescent wave to radiation.

Methods

In this section, we explain our methods to treat electromagnetic fields for radiation from the nonmagnetic Maxwell's fisheye sphere. This is a problem to solve inhomogeneous partial differential equations in mathematics. We first write Maxwell's equations in frequency domain according to Fourier transform. Second, we separate the whole current density or the source going through whole infinite space into two parts. The solution in uniform space (outside Maxwell's fisheye sphere), is also calculated through dyadic Green's function. Interested readers shall see more detail in Supplementary information I(iv). The other one inside Maxwell's fisheye sphere shall be solved via dyadic Green's function narrated in Supplementary information I(i–iii). The sum of both field solutions above make up the complete solution of electromagnetic fields. After that, inverse Fourier transform provides us solutions in time domain:

Famous Fast-Fourier Transform can be a numerical solution to this infinite transform22,23. The explicit expression of Green tensor for the full Maxwell fisheye in impedance-matched case is also given in Supplementary information III.