Introduction

Recently, very small ferromagnets have been included in electronic devices, leading to the field of spintronics1,2. Examples include giant magnetoresistance sensors, magnetic tunnel junctions and spin-transfer torque nanopillars3,4,5,6,7,8,9,10. As the diameter of a ferromagnetic particle decreases toward one nanometer, the particle's magnetization becomes highly susceptible to perturbations by the noise in the environment. In the well known example of superparamagnetism, the magnetization of a ferromagnetic particle is perturbed by thermal noise. Above the blocking temperature, the particle looses the ability to maintain magnetic memory11,12. The magnetization of a ferromagnetic particle may also be susceptible to perturbations by electron transport13. At finite current through a ferromagnetic particle in a double barrier device, the magnetization can exhibit nonequilibrium noise14,15,16. Similar to how the thermal noise limits the size of magnetic memory, further miniaturization of spintronics may be limited by the nonequilibrium noise.

In this report, we present an experimental study of nonequilibrium magnetization noise in a single nanometer-scale Co particle, which is attached between two Al leads by tunneling junctions. Tunneling spectroscopy of discrete levels in similar Co particles have been carried out previously17,18. Magnetic anisotropy fluctuations were introduced to address the unexpected dependence of electron-in-a-box levels on the applied magnetic field18,19,20,21,22,23. A much larger than expected abundance of levels, observed in a Co particle, was explained by nonequilibrium spin excitations, described as a ladder of transitions between states with different spin of the particle (S0)19,20. In these transitions driven by electron tunneling, only the ground states |S0, S0 > with different S0 (spin ground states) are involved19,20. Tunneling transitions between different magnetic states, which will be referred to here as magnetic tunneling transitions, were not observed18,19,20. Examples of magnetic tunneling transitions could be |S0, S0 > → |S0 ± 1/2, S0 ± 1/2 − n >. Because of the spin-orbit (SO) interaction, the magnetic states become admixtures of ŜZ eigenstates |S0, S0 − n >, which fluctuate among various particle eigenstates because of the magnetic anisotropy fluctuations. Thus, the tunneling selection rule ΔSZ = ± 1/2 is not applicable. In that case, we would expect an abundance of magnetic levels in the tunnel spectrum, but the magnetic levels were not demonstrated. In this report, a magnetic level (ω) refers to the magnetic energy difference between the final and the initial state in the magnetic tunneling transition. Despite the absence in the experimental data, magnetic tunneling transitions are widely supported by prior theoretical work20,22,24,25. The magnetic levels cannot be measured by tunneling spectroscopy for the following two reasons: (i) In a magnetic field where the Zeeman energy is much larger than the magnetic anisotropy energy per spin, ω is approximately equal to the Zeeman splitting, which is large enough to resolve by conventional tunneling spectroscopy26. But in that case, the admixing between different ŜZ eigenstates becomes weak. Neglecting the admixing entirely, the tunneling matrix elements for magnetic tunneling transitions with low n are on the order , related to the Clebsch-Gordan (CG) coefficients20. The corresponding tunneling transition probability of order O(1/S0) is negligibly small and only tunneling transitions between spin ground states (|S0, S0 > → |S0 ± 1/2, S0 ± 1/2 >) retain significant weight19,20,24. As a result, in the strong magnetic field, all measured levels display linear dependence on magnetic field without Zeeman splitting17,18. (ii) In the vicinity of the magnetic switching field before the magnetic switch, magnetic levels become so small that they cannot be resolved at experimentally accessible temperature20,25, even though the tunneling matrix elements for the magnetic tunneling transitions could be strongly enhanced by the SO-interaction, as will be discussed here. The main theme of this report is that the nonequilibrium noise is the strongest just below the switching field, where the magnetic levels are small compared to the anisotropy; while in the strong magnetic field, where the magnetic levels are much larger than the anisotropy, the nonequilibrium noise becomes negligibly weak.

Results

Spectroscopic Measurements

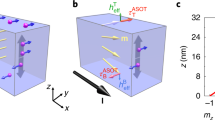
Our samples consist of Co particles tunnel-coupled with two Al leads via aluminum oxide barriers. See section Methods for the description of the sample fabrication. Co particles were formed by deposition of a thin Co film, with nominal thickness of 0.5 nm, on aluminum oxide substrate. At this nominal thickness, we suppose that the deposited Co forms isolated particles of diameter 1–4 nm, as demonstrated by prior work17. Fig. 1a shows the micrograph of our typical device and Fig. 1b displays a transmission electron microscope (TEM) image of aluminum oxide surface topped of by Co film with the nominal thickness 0.5 nm. The image in Fig. 1b is lower in resolution, but generally in agreement with the TEM image in Ref. 17, which showed that Co particles are darker than the substrate. The diameters of the particles in Fig. 1b appear to be in the similar range as in Ref. 17. 36 samples were studied in detail at 4.2 K and approximately two thirds of those samples display bias voltage dependence of the switching field similar to that discussed here, the remaining samples did not display bias voltage dependence of the switching field. Four samples were studied in detail at dilution refrigerator temperature, the main results discussed in this report have been confirmed in three of those samples. In this paper we discuss the electron transport properties in one sample at dilution refrigerator temperature and in another sample at 4.2 K.

Figure 1
figure 1

(a) Scanning electron micrograph of a typical sample. (b) TEM image of Co particles on aluminum oxide surface. (c) Current (red) and differential conductance (blue) versus voltage for sample 1.

Full size image

Fig. 1c shows the current-voltage characteristics, I(V) and the tunnel spectrum, dI/dV of sample 1 at T = 15 mK and zero applied magnetic field. The low voltage region where the current is negligibly small indicates Coulomb blockade, while the steps in the I(V) curve indicate discrete levels, similar to the prior work26. The Coulomb-blockade voltage threshold is the voltage at the first maximum in dI/dV. The particle size will be estimated later in the text.

Fig. 2a and b displays the magnetic field dependence of the tunneling spectrum, for decreasing and increasing magnetic fields, showing symmetric hysteresis about zero magnetic field. Discrete levels correspond to the maximum in conductance. All levels are discontinuous at the same switching field |Bsw| ≈ 0.3 T, confirming that they belong to the same particle. To convert from voltage to electron energy in units of eV, the voltage needs to be divided by 1 + 1/c, where c = 1.59 is the capacitance ratio, obtained as the ratio of the magnitudes of the Coulomb-blockade voltage thresholds at negative and positive bias (see Supplementary Fig. S1 online). The size of the sudden jump in energy levels fluctuates: levels a,b,c and d,(Fig. 2a) change discontinuously by −0.3 meV, 0.07 meV, −0.09 mev and 0.15 meV, respectively. In addition, there is a continuous dependence of the levels versus magnetic field, which varies among levels. These properties are in agreement with the prior experimental work17,18 and theory21,23. The fluctuations in the discontinuity among different levels were explained in terms of the fluctuations in the magnetic anisotropy energy among different particle eigenstates18,19,21,23. All the low-lying levels displayed in Fig. 2b shift down in voltage with the magnetic field, with approximately the same slope. As explained in Ref. 18, in that case, the measured levels correspond to the tunneling transitions where an electron tunnels off the minority electron-in-a-box states, without exciting the particle magnetically. The one level that shifts up in voltage, between 7 mV and 8 mV, is a majority electron-in-a-box level.

Temperature dependence of equilibrium switching field

We measure the temperature dependence of the equilibrium switching field, i.e. the switching field at zero current. We set the voltage to 2.4 mV and measure the magnetic hysteresis loop, following the white arrows in the (B,V) space shown in Fig. 2a. At low temperatures, if the magnetic field is just below the switching field, the particle will face Coulomb blockade. As the magnetic field is increased and reaches the switching field, the transition to a current-carrying state takes place. Since the sequential tunnel current is zero before the switching, this switching field is the equilibrium switching field. The magnetic hysteresis loop for two different temperatures is displayed in Fig. 2c, with the inset showing the temperature dependence of the equilibrium switching field. The error bar is the standard deviation (S.D.) of the equilibrium switching field. The S.D. increases versus temperature. At 4.2 K, thermal broadening produces a current of ≈ 0.1 pA preceding the switching event, but the current is still small enough to have negligible nonequilibrium effect on the switching field (see the next paragraph). The decrease of the equilibrium switching field accompanied by an increase in the S.D. with temperature indicates thermally activated switching27,28,29. By fitting the temperature dependence of the equilibrium switching field to the Néel-Brown model of magnetic reversal11,12,29, we obtain B0 = 0.359 ± 0.036 T for the equilibrium switching field at zero temperature EB = 20.6 ± 2 meV for the energy barrier for switching extrapolated to zero magnetic field. (For a magnetic field B in the vicinity of B0, the energy barrier is EB(1 − B/B0)3/2.29,30) The fit is shown by the solid line in the inset of Fig. 2c (see Supplementary Methods online).

In order to characterize the Co particle, we use a magnetic model-Hamiltonian with uniaxial anisotropy K, based on Stoner-Wohlfarth (SW) model,

The easy-axis is in Z direction and S0 is the total particle spin in units of . The SO-interaction in this Hamiltonian is described by a single magnetic anisotropy constant K, which we refer to as trivial SO-interaction. g = 1.25 is obtained from the difference in slopes of minority and majority electron-in-a-box levels in Fig. 2b. Because the energy levels of the Co particle discussed here exhibit continuous magnetic field dependence before the magnetic switch, which demonstrates that there is a continuous rotation of the magnetization before the switch, the easy-axis cannot be collinear with the magnetic field. Similarly, the easy axis cannot be perpendicular to the magnetic field, because there would be no discrete magnetic switching in that case. We have confirmed that using 15–75 degrees as angle between the easy-axis and the magnetic field produces similar result in the analysis. Thus, we use 45 degrees in further analysis, which is the same assumption as in Refs. 18,19. The SW-switching field B0 for the Hamiltonian given by Eq. 1 could be obtained from gμBB0 = K, which is the equilibrium magnetic switching field at zero temperature. B0 is 0.359 T from the temperature dependence of switching field discussed above, so K = 26.0 μeV. At 45 degrees, we obtain from Eq. 1 that . This corresponds to a hemispherical particle with diameter 2.6 nm and the number of Co atoms Na = 882 24.

Current and voltage dependence of switching field

Now, we study the effect of bias voltage and tunnel current on magnetic switching at T = 60 mK. We set a bias voltage, vary the applied magnetic field and measure the tunnel current. Figs. 3a and 3b, show the magnetic switching field versus voltage and the current recorded immediately prior to the switching, respectively. Note that the tunnel current of 0.1 pA at 60 mK has negligible effect on the switching field. At 10 mV, the magnetic switching field is reduced by 15% compared to the equilibrium switching field at 60 mK. It can also be seen that the decrease in the switching field with bias is accompanied by an increase in the noise of the switching field. The equilibrium switching field at 60 mK has a S.D. of 3.1 mT, while the S.D. at 8 mV bias voltage is 4.7 mT. The magnetic temperature (TM) at voltage V and current I can be defined as the temperature at which the equilibrium switching field equals the switching field at voltage V and current I and base temperature (60 mK in our magnetic field sweeps). TM can be obtained by linearly interpolating the switching field measured at voltage V and base temperature to the temperature dependence of the equilibrium switching field. As temperature is an indicator of thermal noise intensity, magnetic temperature TM serves to represent the level of nonequilibrium magnetization noise. For example, at 8 mV, the average magnetic switching field is 0.281 T. A switching field of 0.281 T is the same as the interpolated equilibrium switching field at 2.36 K. Thus, TM at 8 mV is 2.36 K. The S.D. of the equilibrium switching field at 2.36 K is 4.9 mT, close to the S.D. of the switching field at 8 mV and 60 mK, confirming that the reduction in switching field is well described by the concept of magnetic temperature. The physical interpretation of kBTM is the average magnetic excitation energy in the steady state. The voltage dependence of the switching field cannot be interpreted in terms of a simple shift in magnetic anisotropy with bias voltage, as described in Refs. 31,32,33,34, because in our case, the noise increases with bias voltage. If the switching field simply shifted down due to the change in anisotropy with voltage, the noise would also go down, because the switching field noise scales with the switching field29,35. The magnetic temperature versus voltage and current is shown in Figs. 3a and b, respectively.

Fig. 4a displays the bias voltage dependence of the switching field as well as the S.D. in sample 2, at 4.2 K. In this sample, the magnetic hysteresis loop was measured nine hundred to five thousand times for different bias voltages, enabling us to obtain the statistical distribution of the switching field. As seen in Fig. 4b, the distribution is asymmetric, as expected for thermally activated magnetic switching35. As the bias voltage increases, the distribution broadens asymmetrically, indicating again that the noise increases.

Discussion

The observation that the switching field distribution widens with current, brings a question if simple Joule heating in the environment is responsible for the noise increase. The answer is no because of the following three reasons. First, we take advantage of the full-width-half-maximum (FWHM) of the levels. It is known that the FWHM of a discrete level in a quantum dot is ≈ 3.5kBTe, where Te is the electron temperature in the lead. After conversion from voltage to energy, FWHM becomes 75 μeV and 86 μeV, for the levels at 2.4 mV and 6.3 mV in Fig. 1c, corresponding to Te of 0.25 K and 0.28 K, respectively. So the magnetic temperature is at least an order of magnitude larger than the electron temperature in the leads. Note Te is significantly larger than that obtained by tunneling spectroscopy of discrete levels in Al particles42, implying an additional broadening mechanism in the Co particle. Second, we have estimated the increase in phonon temperature in the particle. Assuming the power input of IV = 40 fW (at 8 mV) into the phonon bath is uniform within the volume of the particle and heat conductance through the tunnel barrier 2.5 × 10−5 W/K-cm for Al2O3 at 60 mK36, we find an increase in the phonon temperature to be in the mK-range. Third, it would be in disagreement with prior work that applied power of 40 fW could raise the temperature of the particle from mK to 2 K. For example, in Ref. 26, the electron temperature remains well below 0.5 K when an order of magnitude larger power was applied to a similarly sized Al particle.

We conclude that the electron tunneling is responsible for the direct deposition of the magnetic energy in the particle, without heating up the environment. At a fixed bias voltage, let EM and denote the magnetic excitation energy and its increment in an electron tunneling event, respectively, averaged over a large number of electron tunneling events. If the SO-interaction is trivial, then will be independent of EM provided EM ≪ EB14. That is, the average energy transfer into the magnetic subsystem per electron tunneling event, is independent of the initial magnetic energy. As will be shown here, that remains to be the case even if the nontrivial SO-interaction is included. Then, EM varies versus time according to the differential equation , where T1 is the magnetization relaxation time. Here we assume that is pumped at the rate 2I/e, since there are two energy deposition events in one sequential tunneling cycle, one for electron tunneling on and one for electron tunneling off. (see Supplementary Note online) The average magnetic excitation energy in the steady state, which could be indicated by the magnetic temperature, becomes

As discussed earlier, most of the levels displayed in Fig. 2b are minority electron-in-a-box levels that do not involve magnetic levels. If the magnetic tunneling transitions were also observed in the tunneling spectra, then those minority electron-in-a-box levels would split by ω. The black line in Fig. 2b indicates the lowest conductance maximum, which moves down in voltage versus field. The black dashed line in Fig. 2b is an example of where a magnetic level is expected, assuming ω is the level spacing from the magnetic Hamiltonian in Eq. 1. If the magnetic level were detected, it would present as a local maximum in the conductance versus voltage, which moves following the dashed line. Evidently, the magnetic level is absent, in agreement with the prior published work17,18. Theoretically, if the SO-interaction were trivial, then we would expect that , which would certainly explain the absence of magnetic levels. The factor 1/2S0 is the probability of a magnetic transition in a tunneling event, related to the square of the CG coefficient involved in that transition14,19,20,24.

Now, assume is valid in the magnetic field just below the magnetic switching field. We obtain ω as the level spacing in Hamiltonian 1 above the metastable spin-ground state. Then, according to Eq. 2 and the data in Fig. 3, we obtain to be in the kHz range. The magnetization relaxation rate reached here seems unphysical, as it is much smaller than that generally measured by ferromagnetic relaxation37. This problem can be resolved if is strongly enhanced just below the switching field, meaning that the magnetic levels are significantly more involved in electron tunneling. Such an enhancement of near the switching field would not be possible if the magnetic transition probabilities are governed exclusively by the CG coefficients14,20,24.

Clearly, the effects of SO-interaction on magnetic tunnel transitions need to be considered beyond the magnetic Hamiltonian in Eq. 1. In the simplest non-trivial approach, we invoke the magnetic model-Hamiltonian for a single Co particle from Refs. 18,19,

N is the total number of electrons in the particle. In the regime of sequential electron tunneling, N can only vary by 1. This model-Hamiltonian was used successfully to account for the magnetic field dependence of the low-lying levels in the tunneling spectra of Co particles consistent with our work. In contrast to Eq. 1, KN now fluctuates with N as well as different particle eigenstates involved in each electron tunneling event18,19,20,21,23. Since the statistics from four levels in Fig. 2a is insufficient to obtain the standard deviation σ(ΔKN) reliably, we use the theoretical value σ(ΔKN) = 0.4 μeV for the particle with Na = 882, which is “of the order needed to account for the experimental data”23.

Because of the fluctuations in KN18,19,20,21,23, many matrix elements of the tunnel Hamiltonian, taken between magnetic states corresponding to different KN, become large in the vicinity of B0 resulting in a much larger . We have derived a formalism, which describes the nonequilibrium distribution among magnetic states at finite bias voltage, using the tunnel Hamiltonian and master equations14 as well as the model-Hamiltonian with fluctuating anisotropy. The discussion of this formalism is beyond the scope of this report. The formalism shows that a simple classical model can be applied to predict the magnetic temperature in the regime of our experiment, so in the remainder of this paper we will use the classical approach only, for simplicity.

Despite the complexity of anisotropy fluctuation, our analysis can be carried by using two different anisotropy constants in for N and N + 1. We can set KN = 26.0 μeV and KN+1 = KN + σ(ΔK) = 26.4 μeV. Fig. 5a shows the magnetic energy of the particle versus mZ = SZ/S0, using the classical energy corresponding to the Hamiltonian given by Eq. 3, for B = 0.281 T, KN and KN+1. The minima in energy are metastable, that is, they correspond to the magnetization directions before switching. We assume that the initial magnetization direction corresponds to the minimum for the anisotropy constant KN. Next, an electron tunneling onto the particle changes the anisotropy constant to KN+1. Tunneling can be considered as instantaneous, because the magnetization precession time ([planck]/KN) is much larger than the time to tunnel under the barrier. In that regime, the tunneling transition is represented by the vertical arrow in the figure. The magnetization is now excited with the classical excitation energy . Here represents the metastable equilibrium SZ of Eq. 3 at X-electron state. Fig. 5b shows that increases as the magnetic field approaches B0. For comparison, in Fig. 5b, we plot using the quantum mechanical approach mentioned earlier. The results from the two approaches agree with each other very well, except in the close proximity of the SW-switching field B0 = KN/gμB. However, in our experiment, the magnetization of the particle always switches before the magnetic field reaches this regime where the classical method breaks down. has a maximum immediately before the magnetic switch at B = B0. It drops to immediately after the magnetic switch at the SW-switching field. In a field B≫B0, which is much smaller than the magnetic level ω≈KNB/B0. This behavior of is consistent with the observation that the magnetic temperature increases with bias in the vicinity of the switching field, while there are no signatures of magnetic levels in the tunnel spectra in a strong magnetic field. The classical excitation energy increases with ΔK = KN+1−KN, indicating that anisotropy fluctuation plays the crucial role in delivering magnetic excitations (Fig. 5b inset). becomes comparable to ω≈ω/2S0(the average magnetic excitation energy per tunneling event if the SO-interaction were zero or trivial) at the magnetic field of S0B0σ(ΔK)/KN≈ 10B0, which is independent of the particle's volume. Thus, the magnetic tunneling transitions are governed by the CG coefficients in a magnetic field above approximately 10B0, while below that field, the magnetic tunneling transitions are governed by the SO-interaction. This is an important result of this report. Interestingly, the same factor S0σ(ΔK)/K accounts for the enhancement of the discontinuities of the electron-in-a-box levels at the switching field18.

Next, we use the stochastic Landau-Lifshitz-Gilbert (LLG) equation to model magnetization dynamics37,

where is the unit vector of magnetic moment, α is the phenomenological damping parameter and is the effective magnetic field with time dependent noise KN(t), which reflects the mesoscopic fluctuations in KN. By numerically solving the LLG equation, we obtain the time dependence of the classical magnetic excitation energy EM driven by KN(t). The numerical solution shows that EM, averaged over a time interval much longer than the correlation time for KN and much shorter than T1, will increase linearly versus time, if it is initially at 0. This verifies the hypothesis used in the derivation of Eq. 2 that is independent of EM. The magnetic temperature is obtained as the steady state value of EM, averaged over time. The numerical solution confirms Eq. 2, , where δf is the rate at which KN changes. The resulting is now in the MHz range, which is more realistic than that obtained from the CG coefficients14,24, demonstrating the relevance of our approach. The magnetization relaxation rate obtained here is consistent with the previous reports18,38,39.

In summary, we find that electron tunneling through a nanometer-scale Co particle can excite nonequilibrium magnetization noise at very low temperatures. This noise can reduce the magnetic switching field as well as broaden its distribution. The noise is strongly enhanced in the vicinity of the magnetic switching field. Magnetic anisotropy fluctuations among different particle eigenstates, caused by the spin-orbit interaction, provide a natural explanation of the noise properties.

The results presented in this report may have ramifications with respect to further miniaturization of spin electronics. It suggests that, other than simple heating, nonequilibrium could present as an explanation for the reduction in switching field. If one of the leads were ferromagnetic, then the magnetization of the ferromagnetic particle could be switched by the STT mechanism40. Relatively long T1 suggested in a Co particle18,38,39 also implies that the critical current for STT-switching should be reduced, because the critical current in STT-switching generally scales with magnetization relaxation rate41. But, since the magnetic tunneling transitions in a Co particle at low field seems to be governed by the SO-interaction which produces anisotropy fluctuations beyond experimental control, it would appear that STT-switching cannot be realized in a Co particle in a double barrier device. That is, the effect of STT would be negligibly weak compared to the effect of nonequilibrium noise. Our future work will study nonequilibrium noise and STT in Ni and NiFe particles, which have lower magneto-crystalline anisotropy than Co. Thus, Ni and NiFe particles may exhibit different nonequilibrium noise.

Methods

Sample fabrication

Our samples are made using electron beam lithography (EBL) and shadow deposition42.(see Supplementary Fig. S2 online) First, a polymethilmetachryllate (PMMA) bridge over a SiO2 substrate is defined by EBL. Second, we deposit 10 nm of Al and 1.5–3 nm of Al2O3, along direction 1. Then we oxidize the sample at room temperature in O2 at 3 mPa, for 30 s. Next, we deposit 0.5 nm of Co, 1 nm–1.5 nm of Al2O3, followed by 10 nm of Al, along direction 2. Sample resistance is varied by changing the oxide layer thickness. After lift-off in acetone, the samples are ready to be wired up for measurement.

Measurements

The I(V) curves are measured using an Ithaco current amplifier and are highly reproducible with voltage sweeps. Some of our samples have finite conductance below the lowest discrete level. This conductance is explained in terms of direct tunneling between the leads, through the aluminum oxide surrounding the particle. We refer to it as a leakage conductance of the junction. To correct for the leakage conductance in sample 1, we subtract a linear slope of 0.35 nS from the I(V) curves. In Fig. 2a, the magnetic field varies at a rate of 0.26 mT/s, while the bias voltage varies between -10.2 mV and 10.2 mV at a rate of 0.25 mV/s. The sample wiring is filtered at the mixing chamber using a copper powder filter and a high-loss coaxial wiring with 10 M H z bandwidth. The sample is in a Faraday cage and the filter output is connected coaxially with the cage. There are no unfiltered wires entering the cage. We usually obtain electron temperatures < 100 mK (measured from the line-width of discrete levels in normal metal particles). In Figs. 2c and 3a–b, the magnetic field sweep rate is 8 mT/s. The temperature dependence of the switching field (inset of Fig. 2c) and the standard deviation is obtained by averaging over up to 32 magnetic field sweeps.