Introduction

The quantum Hall effect (QHE) is one of the most striking phenomena in the field of condensed matter physics since its discovery in the 1980s1. It is referred to as integer quantum Hall effect as the Hall conductivity takes values of 2(n + 1)e2/h with an integer . The QHE in two dimensional electron gases is of particular interest. Recently, the experimental realization of graphene, a stable monolayer of carbon atoms2,3, has stimulated additional interest in two dimensional systems4,5. Graphene exhibits quantized conductivity values of 2(2n + 1)e2/h, . Among the unusual transport properties, the quantum spin Hall effect is particularly exciting as it constitutes a new phase of matter6,7. It requires strong spin orbit interaction (SOI) but not an external perpendicular magnetic field. When Kane and Mele7 in a ground breaking study of graphene had proposed a new class of insulators, the topological insulators (TIs), great experimental and theoretical excitement was generated8,9,10,11,12,13. In addition to the quantum spin Hall effect, an analogous quantum valley Hall effect14,15 arises from a broken inversion symmetry, where Dirac fermions in different valleys flow to opposite transverse edges when an in-plane electric field is applied. The quantum valley Hall effect paves the way to electric generation and detection of valley polarization. Since the occurrence of conducting surface states in TIs is related to the SOI13 and SOI is also a crucial criterion for the quantum spin Hall effect, it has been proposed to search for new materials with strong SOI for application in spintronic devices7,13.

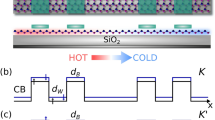
Silicene is a monolayer of silicon16,17 (isostructural to graphene) with very strong SOI. It has a buckled honeycomb structure, see Fig. 1, where the charge carriers behave like massless Dirac fermions18. This breaks the inversion symmetry and gives rise to a quantum valley Hall effect19. Experimental realizations of silicene sheets18,20,21 and ribbons22,23 have been demonstrated by synthesis on metal surfaces. It is believed that silicene opens new opportunities for electrically tunable electronic devices24. Although graphene possesses extraordinary properties, its application in device fabrication is limited by the zero band gap and the difficulty to tune the Dirac particles electrically. Moreover, even if a band gap could be introduced by chemical doping, it would be incompatible with existing nanoelectronics. In the desire to overcome this limitation, the buckling in silicene offers a solution for manipulating the particle dispersion to achieve an electrically tunable band gap. In addition to the latter, silicene has a relatively large band gap of 1.55 meV25 induced by intrinsic SOI, which provides a mass to the Dirac fermions. This mass can be controlled experimentally by an external perpendicular electric field.

Figure 1
figure 1

Honeycomb lattice structure of silicene.

Due to the large ionic radius of silicon the lattice is buckled. The A and B sublattices are shifted by a distance of 2l perpendicular to the silicene sheet to generate a staggered potential in the perpendicular electric field (Ez). We apply a magnetic field (B) perpendicular to the silicene sheet in order to study the valley polarized quantum Hall effect.

Full size image

In the light of the above discussion, silicene is likely to show significant signatures of QHE as well as TI quantum phase transitions. The QHE is the fundamental transport process under an external perpendicular magnetic field. For intrinsic SOI and an external perpendicular electric field, we show in the following that the quantum phase transition from a two dimensional TI to a trivial insulator is accompanied by quenching of the QHE and onset of a valley quantum Hall effect (VQHE), providing a tool to experimentally tune the topological state of silicene. We use the Kubo formalism to discuss the Hall conductivity and address the longitudinal conductivity for elastic impurity scattering in the first Born approximation.

Results

We model silicene by an effective Hamiltonian in the xy-plane. An external magnetic field (0, 0, B) is applied perpendicular to the silicene sheet, taking into account SOI and electric field19,26,27. Dirac fermions in buckled silicene obey the two-dimensional graphene-like Hamiltonian

Here, η = +/− denotes K/K′, Δz = lEz, where Ez is the uniform electric field applied perpendicular to the silicene sheet, with l = 0.23 Å. In addition, (σx, σy, σz) is the vector of Pauli matrices and v denotes the Fermi velocity of the Dirac fermions. Spin up (↑) and down (↓) is represented by s = +1 and −1, respectively. Moreover, p = p + eA/c is the two dimensional canonical momentum with vector potential A and c is the speed of light. Using the Landau gauge with vector potential (0, Bx, 0) and diagonalizing the Hamiltonian given in Eq. (1) we obtain the eigenvalues

Here, t = +/− denotes the electron/hole band, and n is an integer. The eigenfunctions for the K′ point can be obtained by exchanging the electron and hole eigen-states in the K point solution with φn−1 interchanged by φn. For more details see the supplementary information (Section I).

In the presence of a magnetic field there are two contributions to the magnetoconductivity: the Hall and longitudinal conductivities. The latter is the localized state contribution responsible for Shubnikov de Haas (SdH) oscillations. The Hall conductivity is the non-diagonal contribution. In order to calculate the electrical conductivity in the presence of SOI, an electric field and a perpendicular magnetic field, we employ the general Liouville equation28. The Hall conductivity σxy is obtained from the non-diagonal elements of the conductivity tensor as29,30

Solving and simplifying, see the supplementary information (Section II), yields in the limit of zero temperature

with . This result is identical to the integer quantum Hall effect in graphene2,3,29,30 for Δz = ΔSO = 0, where the plateaus appear at ±2, ±6, ±10, … , as shown in Fig. 2. For Δz = 0 and ΔSO ≠ 0 there is a plateau at the charge neutrality point (CNP) in Fig. 2(top), which confirms that silicene is gapped due to strong SOI. The parameters used in Figs. 2 to 5 are N = 1 × 1015 m−2, μB = 5.788 × 10−5 eV/T, ne = 5 × 1015 m2, k0 = 10−7 m−1, v = 5 × 105 m/s and .

Figure 2
figure 2

Hall (top) and longitudinal (bottom) conductivities as functions of the Fermi energy for 0 meV (black line) and 4 meV (red line) SOI energy.

T = 2 K, Δz = 0 meV and B = 1 T. This situation represents a trivial insulator.

Full size image

Furthermore, we show the Hall conductivity in Fig. 3(top) as a function of the Fermi energy for fixed values of the magnetic field and temperature. We find plateaus in the Hall conductivity at 0, ±1, ±3, ±5, … for both valleys in the limit of large electric field energy (Δz > ΔSO). The total Hall conductivity of the K and K′ valleys together for Δz > ΔSO > 0 and Δz = ΔSO is presented in Fig. 4(top). The extra plateaus at 0 and reflect the quantum phase transition which lifts the four-fold degeneracy of the n = 0 Landau level (LL). This is not possible in graphene. Moreover, for Δz = ΔSO = 4 meV we find a single peak at the CNP with electron hole symmetry and plateaus at ±1, ±3, ±5, … . This corresponds to the semimetallic state of the system31. There are three major differences between silicene and graphene: First, the electrical effects due to buckling polarize all LLs. Second, the SOI is much stronger. Third, the spin and valley degeneracy factor 4 is missing in the prefactor of Eq. (4). This demonstrates that the surface states of the silicene TI have a strong spin texture structure, which is distinct from the ideal Dirac fermions in graphene and results in a different quantum Hall conductivity. We note that the n ≠ 0 LLs are still doubly degenerate, consisting of spin up and down states from different valleys. The factor of 2 in the prefactor of Eq. (4) is due to this degeneracy.

Figure 3
figure 3

Hall (top) and longitudinal (bottom) conductivities as functions of the Fermi energy for 7 meV electric field energy.

T = 2 K, ΔSO = 4 meV and B = 1 T. Black lines correspond to the K valley and red lines to the K′ valley. This situation represents a Hall insulator.

Full size image
Figure 4
figure 4

Total (K+K′) Hall (top) and longitudinal (bottom) conductivities as functions of the Fermi energy for 7 meV (black line) and 4 meV (red line) electric field energy.

T = 2 K, ΔSO = 4 meV and B = 1 T. The red line (Δz = ΔSO = 4 meV) represents the semimetallic state.

Full size image

We argue that silicene undergoes a quantum phase transition from a trivial insulator, in which the Hall conductivity at the CNP is zero, to a Hall insulator, in which the Hall conductivity equals e2/h. The transition happens when Δz > ΔSO > 0 and is associated with a non-analytic contribution to the conductivity from the n = 0 LL. The transition is the result of a change in the character of the n = 0 LL, see Eq. (2), which happens in each valley independently. For Δz = 0 one of the n = 0 sublevels is electron-like and the other hole-like in both valleys. When the electric field energy exceeds the SOI, both sublevels are electron-like for the K valley and hole-like for the K′ valley. The Hall conductivity in Eq. (4) evaluated for zero Fermi energy jumps from 0 (Δz = 0, ΔSO > 0) to ±e2/h (Δz > ΔSO) by tuning the electric field.

To obtain the longitudinal conductivity, we assume that the electrons are elastically scattered by randomly distributed charged impurities, as it has been shown that charged impurities play the key role in the transport in silicene near the Dirac point. This type of scattering is dominant at low temperature. If there is no spin degeneracy, the longitudinal conductivity is given by28,29,30

Here, f(Eξ) is the Fermi Dirac distribution function, with f(Eξ) = f(Eξ′) for elastic scattering, kB is the Boltzmann constant and EF is the chemical potential. Wξξ′(Eξ, Eξ′) is the transmission rate between the one-electron states |ξ〉 and |ξ′〉 and e is the charge of the electron. Conduction occurs by transitions through spatially separated states from xξ to xξ′, where xξ = 〈ξ|x|ξ〉. The londitudinal conductivity arises as a result of migration of the cyclotron orbit due to scattering by charged impurities. A detailed derivation is given in the supplementary information (Section III).

In general, the oscillatory part of the longitudinal conductivity in Eq. (5) is expressed as

A closer analytical examination of this result establishes an oscillation with the SdH frequency due to the distribution function entering the expression. For Δz = ΔSO = 0 we have a symmetric electron-hole spectrum of the magnetoconductivity with a single peak at the CNP, see Fig. 2(bottom). This situation is the same as for the Dirac fermions in graphene2,3,29,30. We obtain a gap at the CNP for Δz = 0 and ΔSO > 0 with electron-hole symmetry. For Δz > 0, silicene undergoes a quantum phase transition at the CNP and a well resolved splitting of the SdH oscillations appears. Figure 3(bottom) reveals an oscillatory behavior with the period of the SdH oscillations for the K valley (black line) and the K′ valley (red line) for Δz > ΔSO > 0. This non-trivial behavior is due to the interplay of SOI and electric field and is highlighted in Fig. 3(bottom). The splitted peak is shifted to the electron and hole region for the K and K′ valley, respectively, when the electric field energy grows relative to the SOI energy. This shift of the n = 0 LL is consistent with the energy spectrum in Eq. (2). In effect, the longitudinal conductivity at the CNP passes from a minimum to a maximum by tuning the electric field, i.e., the system undergoes a transition from a trivial insulator to a Hall insulator. The behaviour can be characterized as a quantum phase transition. For n = 0 Eq. (6) gives in the limit of low temperature or high magnetic field , which is consistent with the eigenenergy spectrum of Eq. (2). This fact clearly indicates a lifting of the four-fold degeneracy of the n = 0 LL and a quantum phase transition at the CNP.

The total Hall (top) and longitudinal (bottom) conductivities of both valleys together are addressed in Fig. 4. For Δz = ΔSO, we see a splitting of the n = 0 LL into three peaks, one at the CNP and two with electron-hole symmetry. The energy gap between the spin up bands closes, while the spin down bands maintain a gap. This situation corresponds to the semimetallic state of silicene31. To observe the effect experimentally, the temperature broadening of the LLs must be less than the SOI energy, which can be achieved at low temperature. Finally, we show the total Hall and longitudinal resistivities as a function of the magnetic field in Fig. 5. These results refer to the regime Δz > ΔSO > 0 with Δz = 15 meV and ΔSO = 5 meV to cleary see the VQHE. We find that steps between the plateaus coincide with sharp peaks of the longitudinal resistivity. For high magnetic field, we find a significant splitting of the Hall plateaus and the corresponding peaks in the longitudinal resistivity. In contrast, for low magnetic field, we observe a beating pattern of the SdH oscillations due to the energy difference between SOI and electric field for the spin up and down states. The electric field breaks the inversion symmetry and the surface Dirac fermions acquire a mass due to both the SOI and electric field.

Figure 5
figure 5

Total (K+K′) Hall (red lines) and longitudinal (black lines) resistivities as functions of the perpendicular magnetic field for T = 2 K, Δz = 15 meV and ΔSO = 4 meV.

A well resolved splitting of the VQHE in the regime Δz > ΔSO > 0 is evident.

Full size image

Discussion

The following conclusions apply to both conductivities: (i) For Δz = 0 there is a minimum at the CNP due to splitting of the n = 0 LL in two sublevels because of the SOI. (ii) For Δz = ΔSO there is a peak at the CNP with electron-hole symmetry. This corresponds to the semimetallic state. (iii) For Δz > ΔSO we have a splitting of the n = 0 LL into four sublevels (two peaks in the electron and two in the hole region) with a gap at the CNP. All other LLs are also split. We call this a quantum phase transition due to the shifting of electron and hole peaks in the K and K′ valley, respectively. The four-fold degeneracy of the n = 0 LL is fully resolved and all other LLs split into two two-fold degenerate sublevels as the spin up states of one valley coincide with the spin down states of the other valley. This property distinguishes silicene from graphene2,3,29,30.

Our analytical calculations for the Hall and longitudinal conductivities in silicene include an electric field to model electrical tuning in nanoelectronic applications. We have shown that the Hall conductivity is an integer multiple of e2/h with plateaus at 0, ±1, ±3, ±5, … e2/h for Δz > ΔSO, which is a clear signature of the VQHE. The Hall conductivity jumps from 0 to 1 at the critical electric field of the level crossing. This reflects the transition from a trivial insulator to a Hall insulator at the CNP. The derived results also apply to isostructural germanene, for which the SOI is even stronger (ΔSO = 43 meV with l = 0.33 Å). Experimentally, the best way to see the QHE and VQHE is to measure the Hall conductivity as a function of the gate voltage which tunes the chemical potential. In silicene and germanene the temperature will not affect the Hall plateau as the SOI and electric field are strong. We have shown that the energy splitting due to Δz and ΔSO leads to unconventional plateaus in the QHE and VQHE with a quantum phase transition at the CNP. Thus, the QHE, the VQHE and the topological insulating states in silicene and germanene can be observed and tuned experimentally at finite temperature. The fact that the splitting due to the SOI can be controlled by an external electric field (gate voltage) is of great significance for electrically tunable spintronic devices. Our predictions represent a milestone for spin and valley electronics as silicene enables such devices, compatible with the existing technology.