Introduction

Quantum computers are expected to perform some (classical) computational tasks of practical interest, e.g., large integer factorization, with unprecedented efficiency. Quantum simulators, on the other hand, perform tasks of a more “quantum nature”, which cannot be efficiently carried out by a classical computer. Namely, they have the ability to simulate complex quantum dynamical systems of interest. The need to perform tasks of genuine quantum nature is emerging as individual quantum systems play a more prominent role in labs (and, eventually, in everyday life). Examples include: quantum teleportation, dynamical control of quantum systems, or quantum state identification. Quantum information techniques are already being developed in order to execute these tasks efficiently.

This paper is concerned with a simple, yet fundamental instance of quantum state identification. A source produces two unknown pure qubit states with equal probability. A human expert (who knows the source specifications, for instance) classifies a number of 2n states produced by this source into two sets of size roughly n (statistical fluctuations of order should be expected) and attaches the labels 0 and 1 to them. We view these 2n states as a training sample and we set ourselves to find a universal machine that uses this sample to assign the right label to a new unknown state produced by the same source. We refer to this task as quantum classification for short.

Quantum classification can be understood as a supervised quantum learning problem, as has been noticed by Guta and Kotlowski in their recent work1 (though they use a slightly different setting). Learning theory, more properly named machine learning theory, is a very active and broad field which roughly speaking deals with algorithms capable of learning from experience2. Its quantum counterpart3,4,5,6,7 not only provides improvements over some classical learning problems but also has a wider range of applicability, which includes the problem at hand. Quantum learning has also strong links with quantum control theory and is becoming a significant element of the quantum information processing toolbox.

An absolute limit on the minimum error in quantum classification is provided by the so called optimal programmable discrimination machine8,9,10,11,12,13. In this context, to ensure optimality one assumes that a fully general two-outcome joint measurement is performed on both the 2n training qubits and the qubit we wish to classify, where the observed outcome determines which of the two labels, 0 or 1, is assigned to the latter qubit. Thus, in principle, this assumption implies that in a learning scenario a quantum memory is needed to store the training sample till the very moment we wish to classify the unknown qubit. The issue of whether or not the joint measurement assumption can be relaxed has not yet been addressed. Nor has the issue of how the information left after the joint measurement can be used to classify a second unknown qubit produced by the same source, unless a fresh new training set (TS) is provided (which may seem unnatural in a learning context).

The aim of this paper is to show that for a sizable TS (asymptotically large n) the lower bound on the probability of misclassifying the unknown qubit set by programmable discrimination can be attained by first performing a suitable measurement on the TS followed by a Stern-Gerlach type of measurement on the unknown qubit, where forward classical communication is used to control the parameters of the second measurement. The whole protocol can thus be undersood as a learning machine (LM), which requires much less demanding assumptions while still having the same accuracy as the optimal programmable discrimination machine. All the relevant information about the TS needed to control the Stern-Gerlach measurement is kept in a classical memory, thus classification can be executed any time after the learning process is completed. Once trained, this machine can be subsequently used an arbitrary number of times to classify states produced by the same source. Moreover, this optimal LM is robust under noise, i.e., it still attains optimal performance if the states produced by the source undergo depolarization to any degree. Interestingly enough, in the ideal scenario where the qubit states are pure and the TS consists in exactly the same number of copies of each of the two types 0/1 (no statistical fluctuations are allowed) this LM attains the optimal programmable discrimination bound for any size 2n of the TS, not necessarily asymptotically large.

At this point it should be noted that LMs without quantum memory can be naturally assembled from two quantum information primitives: state estimation and state discrimination. We will refer to these specific constructions as “estimate-and-discriminate” (E&D) machines. The protocol they execute is as follows: by performing, e.g., an optimal covariant measurement on the n qubits in the TS labeled 0, their state |ψ0〉 is estimated with some accuracy and likewise the state |ψ1〉 of the other n qubits that carry the label 1 is characterized. This classical information is stored and subsequently used to discriminate an unknown qubit state. It will be shown that the excess risk (i.e., excess average error over classification when the states |ψ0〉 and |ψ1〉 are perfectly known) of this protocol is twice that of the optimal LM. The fact that the E&D machine is suboptimal means that the kind of information retrieved from the TS and stored in the classical memory of the optimal LM is specific to the classification problem at hand and that the machine itself is more than the mere assemblage of well known protocols.

We will first present our results for the ideal scenario where states are pure and no statistical fluctuation in the number of copies of each type of state is allowed. The effect of these fluctuations and the robustness of the LM optimality against noise will be postponed to the end of the section.

Results

Programmable machines

Before presenting our results, let us summarize what is known about optimal machines for programmable discrimination. This will also allow us to introduce our notation and conventions. Neglecting statistical fluctuations, the TS of size 2n is given by a state pattern of the form , where the shorthand notation [·] ≡ |·〉〈·| will be used throughout the paper and where no knowledge about the actual states |ψ0〉 and |ψ1〉 is assumed (the figure of merit will be an average over all states of this form). The qubit state that we wish to label (the data qubit) belongs either to the first group (it is [ψ0]) or to the second one (it is [ψ1]). Thus, the optimal machine must discriminate between the two possible states: either , in which case it should output the label 0, or , in which case the machine should output the label 1. Here and when needed for clarity, we name the three subsystems involved in this problem A, B and C, where AC is the TS and B is the data qubit. In order to discriminate from , a joined two-outcome measurement, independent of the actual states |ψ0〉 and |ψ1〉, is performed on all 2n + 1 qubits. Mathematically, it is represented by a positive operator valued measure (POVM) . The minimum average error probability of the quantum classification process is given by Pe = (1 − Δ/2)/2, where . This average can be cast as a SU(2) group integral and, in turn, readily computed using Schur's lemma to give

where ∥·∥1 is the trace norm and are average states defined as

In this paper stands for the projector on the fully symmetric invariant subspace of m qubits, which has dimension dm = m + 1. Sometimes, it turns out to be more convenient to use the subsystem labels, as on the right of (2). The maximum in (1) is attained by choosing E0 to be the projector onto the positive part of .

The right hand side of (1) can be computed by switching to the total angular momentum basis, , where and −J ≤ M ≤ J (an additional label may be required to specify the way subsystems couple to give J; see below). In this (Jordan) basis12 the problem simplifies significantly, as it reduces to pure state discrimination14 on each subspace corresponding to a possible value of the total angular momentum J and magnetic number M. By writing the various values of the total angular momentum as , the final answer takes the form13:

A simple asymptotic expression for large n can be computed using Euler-Maclaurin's summation formula. After some algebra one obtains

The leading order (1/6) coincides with the average error probability , where is the minimum error in discrimination between the two known states |ψ0〉 and |ψ1〉.

Learning machines

The formulas above give an absolute lower bound to the error probability that can be physically attainable. We wish to show that this bound can actually be attained by a learning machine that uses a classical register to store all the relevant information obtained in the learning process regardless the size, 2n, of the TS. A first hint that this may be possible is that the optimal measurement can be shown to have positive partial transposition with respect to the partition TS/data qubit. Indeed this is a necessary condition for any measurement that consists of a local POVM on the TS whose outcome is fed-forward to a second POVM on the data qubit. This class of one-way adaptive measurement can be characterized as:

where the positive operators Lµ (Dµ) act on the Hilbert space of the TS (data qubit we wish to classify) and . The POVM represents the learning process and the parameter µ, which a priori may be discrete or continuous, encodes the information gathered in the measurement and required at the classification stage. For each possible value of µ, defines the measurement on the data qubit, whose two outcomes represent the classification decision. Clearly, the size of the required classical memory will be determined by the information content of the random variable µ.

Covariance and structure of

We will next prove that the POVM , which extracts the relevant information from the TS, can be chosen to be covariant. This will also shed some light on the physical interpretation of the classical variable µ. The states (2) are by definition invariant under a rigid rotation acting on subsystems AC and B, of the form , where throughout this paper, U stands for an element of the appropriate representation of SU(2), which should be obvious by context (in this case , where u is in the fundamental representation). Since , the positive operator UE0U† gives the same error probability as E0 for any choice of U [as can be seen from, e.g., Eq. (1)]. The same property thus holds for their average over the whole SU(2) group , which is invariant under rotations and where du denotes the SU(2) Haar measure. By further exploiting rotation invariance (see Sec. Methods for full details) can be written as

for some positive operator Ω, where we use the short hand notation . Similarly, the second POVM element can be chosen to be an average, , of the form (6), with instead of [↑]. We immediately recognize to be of the form (5), where u, and Du ≡ u[↑]u† play the role of µ, Lµ and Dµ respectively. Hence, w.l.o.g. we can choose , which is a covariant POVM with seed Ω. Note that u entirely defines the Stern-Gerlach measurement, , i.e., u specifies the direction along which the Stern-Gerlach has to be oriented. This is the relevant information that has to be retrieved from the TS and kept in the classical memory of the LM.

Covariance has also implications on the structure of Ω. In Sec. Methods, we show that this seed can always be written as

where

and j (m) stands for the total angular momentum jAC (magnetic number mAC) of the qubits in the TS. In other words, the seed is a direct sum of operators with a well defined magnetic number. As a result, we can interpret that Ω points along the z-axis. The constrain (8) ensures that is a resolution of the identity.

To gain more insight into the structure of Ω, we trace subsystems B in the definition of Δ, given by the first equality in Eq. (1). For the covariant POVM (6), rotational invariance enables us to express this quantity as

where we have defined

(the two resulting terms in the right-hand side are the post-measurement states of AC conditioned to the outcome ↑ after the Stern-Gerlach measurement is performed on B) and the maximization is over valid seeds (i.e., over positive operators Ω such that ). We calculate Γ↑ in Sec. Methods. The resulting expression can be cast in the simple and transparent form

where is the z component of the total angular momentum operator acting on subsystem A/C, i.e., on the training qubits to which the human expert assigned the label 0/1. Eq. (11) suggests that the optimal Ω should project on the subspace of A (C) with maximum (minimum) magnetic number, which implies that mAC = 0. An obvious candidate is

Below we prove that indeed this seed generates the optimal LM POVM.

Optimality of the LM

We now prove our main result: the POVM , generated from the seed state in Eq. (12), gives an error probability equal to the minimum error probability of the optimal programmable discriminator, Eq. (3). It is, therefore, optimal and, moreover, it attains the absolute minimum allowed by quantum physics.

The proof goes as follows. From the very definition of error probability,

we have

where we have used rotational invariance. We can further simplify this expression by writing it as

To compute the projections inside the norm signs we first write |φ0〉|↑〉 (|φ0〉|↓〉 will be considered below) in the total angular momentum basis |J, M〉(AC)B, where the attached subscripts remind us how subsystems A, B and C are both ordered and coupled to give the total angular momentum J (note that a permutation of subsystems, prior to fixing the coupling, can only give rise to a global phase, thus not affecting the value of the norm we wish to compute). This is a trivial task since |φ0〉|↑〉 ≡ |φ0〉AC|↑〉B, i. e., subsystems are ordered and coupled as the subscript (AC)B specifies, so we just need the Clebsch-Gordan coefficients

The projector , however, is naturally written as . This basis differs from that above in the coupling of the subsystems. To compute the projection we only need to know the overlaps between the two bases A(CB)〈J, M|J, M〉(AC)B. Wigner's 6j-symbols provide this information as a function of the angular momenta of the various subsystems.

Using the Clebsch-Gordan coefficients and the overlaps between the two bases, it is not difficult to obtain

An identical expression can be obtained for in the basis |J, M〉(BA)C. To finish the proof, we compute the norm squared of (17) and substitute in (15). It is easy to check that this gives the expression of the error probability in (3), i.e., .

Memory of the LM

Let us go back to the POVM condition, specifically to the minimum number of unitary transformations needed to ensure that, given a suitable discretization of (6), is a resolution of the identity for arbitrary n. This issue is addressed in15, where an explicit algorithm for constructing finite POVMs, including the ones we need here, is given. From the results there, we can bound the minimum number of outcomes of by 2(n + 1)(2n + 1). This figure is important because its binary logarithm gives an upper bound to the minimum memory required. We see that it grows at most logarithmically with the size of the TS.

E&D machines

E&D machines can be discussed within this very framework, as they are particular instances of LMs. In this case the POVM has the form , where and are themselves POVMs on the TS subsystems A and C respectively. The role of and is to estimate (optimally) the qubit states in these subsystems16. The measurement on B (the data qubit) now depends on the pair of outcomes of and : . It performs standard one-qubit discrimination according to the two pure-state specifications, say, the unit Bloch vectors and , estimated with and . In this section, we wish to show that E&D machines perform worse than the optimal LM.

We start by tracing subsystems AC in Eq. (1), which for E&D reads

If we write , we have

where and are the Bloch vectors of the data qubit states

conditioned to the outcomes α and i respectively and , are their probabilities. We now recall that optimal estimation necessarily requires that all elements of must be of the form , where , cα > 0 and {Uα} are appropriate SU(2) rotations (analogous necessary conditions are required for )17. Substituting in Eq. (20) we obtain pα = cα/dn and

(a similar expression holds for ). This means that the Bloch vector of the data qubit conditioned to outcome α is proportional to (the Bloch vector of the corresponding estimate) and is shrunk by a factor n/dn+1 = n/(n+2) = η. Note in passing that the shrinking factor η is independent of the measurements, provided it is optimal.

Surprisingly at first sight, POVMs that are optimal and thus equivalent, for estimation may lead to different minimum error probabilities. In particular, the continuous covariant POVM is outperformed in the problem at hand by those with a finite number of outcomes. Optimal POVMs with few outcomes enforce large angles between the estimates and and thus between and (π/2 in the n = 1 example below). This translates into increased discrimination efficiency, as shown by (19), without compromising the quality of the estimation itself. Hence the orientation of relative to (which for two continuous POVMs does not even make sense) plays an important role, as it does the actual number of outcomes. With an increasing size of the TS, the optimal estimation POVMs require also a larger number of outcomes and the angle between the estimates decreases in average, since they tend to fill the 2-sphere isotropically. Hence, the minimum error probability is expected to approach that of two continuous POVMs. This is supported by numerical calculations. The problem of finding the optimal E&D machine for arbitrary n appears to be a hard one and is currently under investigation. Here we will give the absolute optimal E&D machine for n = 1 and, also, we will compute the minimum error probability for both and being the continuous POVM that is optimal for estimation. The later, as mentioned, is expected to attain the optimal E&D error probability asymptotically.

We can obtain an upper bound on (19) by applying the Schwarz inequality. We readily find that

where we have used that , as follows from the POVM condition on and . The maximum norm of and is bounded by 1/3 [the shrinking factor η for n = 1]. Thus

where the value of ΔLM can be read off from Eq. (3). The E&D bound is attained by the choices M↑/↓ = [↑/↓] and , where we have used the definition .

For arbitrary n, a simple expression for the error probability can be derived in the continuous POVM case, , where s is a unit vector (a point on the 2-sphere ) and Us is the representation of the rotation that takes the unit vector along the z-axis, z, into s. Here s labels the outcomes of the measurement and thus plays the role of α and i. The continuous version of (19) can be easily computed to be

Asymptotically, we have . Therefore, the excess risk, which we recall is the difference between the average error probability of the machine under consideration and that of the optimal discrimination protocol for known qubit states (1/6), is RE&D = 2/(3n)+…. This is twice the excess risk of the optimal programmable machine and the optimal LM, which can be read off from Eq. (4):

For n = 1, Eq. (23) leads to . This value is already 15% larger than excess risk of the optimal LM: .

Robustness of LMs

So far we have adhered to the simplifying assumptions that the two types of states produced by the source are pure and, moreover, exactly equal in number. Neither of these two assumptions is likely to hold in practice, as both, interaction with the environment, i.e., decoherence and noise and statistical fluctuations in the numbers of states of each type, will certainly take place. Here we prove that the performance of the optimal LM is not altered by these effects in the asymptotic limit of large TS. More precisely, the excess risk of the optimal LM remains equal to that of the optimal programmable discriminator to leading order in 1/n when noise and statistical fluctuations are taken into account.

Let us first consider the impact of noise, which we will assume isotropic and uncorrelated. Hence, instead of producing [ψ0/1], the source produces copies of

In contrast to the pure qubits case, where belongs to the fully symmetric invariant subspace of maximum angular momentum j = n/2, the state of A/C is now a full-rank matrix of the form . Hence, it has projections on all the orthogonal subspaces , where and is the multiplicity space of the representation with total angular momentum j (see Sec. Methods for a formula of the multiplicity ) and j is in the range from 0 (1/2) to n/2 if n is even (odd). Therefore is block-diagonal in the total angular momentum eigenbasis. The multiplicity space carries the label of the different equivalent representations of given j, which arise from the various ways the individual qubits can couple to produce total angular momentum j. For permutation invariant states (such as ), this has no physical relevance and the only effect of in calculations is through its dimension . Hence, the multiplicity space will be dropped throughout this paper.

The average states now become a direct sum of the form

where we use the shorthand notation ξ = {jA, jC} [each angular momentum ranges from 0 (1/2) to n/2 for n even (odd)] and is the probability of any of the two average states projecting on the block labeled ξ. Hence,

The number of terms in Eq. (28), is [(2n+3±1)/4]2 for even/odd n. It grows quadratically with n, in contrast to the pure state case for which there is a single contribution corresponding to jA = jC = n/2. In the asymptotic limit of large n, however, a big simplification arises because of the following results: for each ξ of the form ξ = {j, j} (jA = jC = j), the following relation holds (see Sec. Methods)

where are the average states (2) for a number of 2j pure qubits. Here is the expectation value restricted to of the z-component of the angular momentum in the state , where ρ has Bloch vector rz. Eq. (29) is an exact algebraic identity that holds for any value of j, n and r (it bears no relation whatsoever to measurements of any kind). The second result is that for large n, both and become continuous probability distributions, pn(xA) and pn(xC), where xA/C = 2jA/C/n ∈ [0, 1]. Asymptotically, they approach Dirac delta functions peaked at xA = xC = r (see Sec. Methods). Hence, the only relevant contribution to ΔLM comes from ξ = {rn/2, rn/2}. It then follows that in the asymptotic limit

Hence, mixed-state quantum classification using a TS of size 2n is equivalent to its pure-state version for a TS of size 2nr, provided n is asymptotically large. In particular, our proof of optimality above also holds for arbitrary r ∈ (0, 1] if the TS is sizable enough and . This result is much stronger than robustness against decoherence, which only would require optimality for values of r close to unity.

From Eqs. (28) and (30) one can easily compute ΔLM for arbitrary r using that19 up to exponentially vanishing terms. The trace norm of can be retrieved from, e.g., Eq. (25). For rn pure qubits one has . After some trivial algebra we obtain

for the error probability, in agreement with the optimal programmable machine value given in13, as claimed above. This corresponds to an excess risk of

In the non-asymptotic case, the sum in Eq. (28) is not restricted to ξ = {j, j} and the calculation of the excess risk becomes very involved. Rather than attempting to obtain an analytical result, for small training samples we have resorted to a numerical optimization. We first note that Eqs. (7) through (11) define a semidefinite programming optimization problem (SDP), for which very efficient numerical algorithms have been developed18. In this framework, one maximizes the objective function ΔLM [second equality in Eq. (9)] of the SDP variables Ωm ≥ 0, subject to the linear condition (8). We use this approach to compute the error probability, or equivalently, the excess risk of a LM for mixed-state quantum classification of small samples (n ≤ 5), where no analytical expression of the optimal seed is known. For mixed states the expression of Γ↑ and Ωm can be found in Sec. Methods, Eqs. (57) through (59).

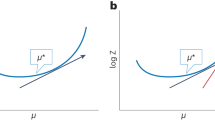
Our results are shown in Fig. 1, where we plot RLM (shaped dots) and the lower bounds given by Ropt (solid lines) as a function of the purity r for up to n = 5. We note that the excess risk of the optimal LM is always remarkably close to the absolute minimum provided by the optimal programmable machine and in the worst case (n = 2) it is only 0.4% larger. For n = 1 we see that RLM = Ropt for any value of r. This must be the case since for a single qubit in A and C one has jA = jC = 1/2 and Eq. (29) holds.

Figure 1
figure 1

Excess risk RLM (points) and its corresponding lower bound Ropt (lines), both as a function of the purity r and for values of n ranging from 1 to 5 (from top to bottom).

Full size image

We now turn to robustness against statistical fluctuations in the number of states of each type produced by the source. In a real scenario one has to expect that jA = nA/2 ≠ nC/2 = jC, nA + nB = 2n. Hence, Γ↑ has the general form (57), which gives us a hint that our choice Ω = Ωm=0 may not be optimal for finite n. This has been confirmed by numerical analysis using the same SDP approach discussed above. Here, we show that the asymptotic performance (for large training samples) of the optimal LM, however, is still the same as that of the optimal programmable discriminator running under the same conditions (mixed states and statistical fluctuations in nA/C).

Asymptotically, a real source for the problem at hand will typically produce mixed copies of each type. In Sec. Methods, it is shown that the relation (30) still holds in this case if n is large. It reads

(δ first appears at order n−3/2). Hence, the effect of both statistical fluctuations in nA/C and noise (already considered above) is independent of the machine used for quantum classification (i.e., it is the same for LM, programmable machines, E&D, …). In particular, the relation (32), RLM = Ropt, between the excess rate of the optimal LM and its absolute limit given by the optimal programmable discriminator still holds asymptotically, which proves robustness.

Discussion

We have presented a supervised quantum learning machine that classifies a single qubit prepared in a pure but otherwise unknown state after it has been trained with a number of already classified qubits. Its performance attains the absolute bound given by the optimal programmable discrimination machine. This learning machine does not require quantum memory and can also be reused without retraining, which may save a lot of resources. The machine has been shown to be robust against noise and statistical fluctuations in the number of states of each type produced by the source. For small sized training sets the machine is very close to optimal, attaining an excess risk that is larger than the absolute lower limit by at most 0.4%. In the absence of noise and statistical fluctuations, the machine attains optimality for any size of the training set.

One may rise the question of whether or not the separated measurements on the training set and data qubit can be reversed in time; in a classical scenario where, e.g., one has to identify one of two faces based on a stack of training portraits, it is obvious that, without memory limitations, the order of training and data observation can be reversed (in both cases the final decision is taken based on the very same information). We will briefly show that this is not so in the quantum world. In the reversed setting, the machine first performs a measurement , with each element of rank one and stores the information (which of the possible outcomes is obtained) in the classical memory to control the measurement to be performed on the training set in a later time. The probability of error conditioned to one of the outcomes, say ↑, is given by the Helstrom formula , where Γ↑ is defined in Eq. (10). Using Eq. (11) one has . The averaged error probability is then

In the limit of infinite copies we obtain , which is way larger than . The same minimum error probability of Eq. (34) can be attained by performing a Stern-Gerlach measurement on the data qubit, which requires just one bit of classical memory. This is all the classical information that we can hope to retrieve from the data qubit, in agreement with Holevo's bound20. This clearly limits the possibilities of a correct classification —very much in the same way as in face identification with limited memory size. In contrast, the amount of classical information “sent forward” in the optimal learning machine goes as the logarithm of the size of the training sample. This asymmetry also shows that despite the separability of the measurements, non-classical correlations between the training set and the data qubit play an important role in quantum learning.

Some relevant generalizations of this work to, e.g., higher dimensional systems and arbitrarily unbalanced training sets, remain an open problem. Another challenging problem with direct practical applications in quantum control and information processing is the extension of this work to unsupervised machines, where no human expert classifies the training sample.

Methods

Block-diagonal form of

The state of n identical copies of a general qubit state ρ with purity r and Bloch vector rs, has a block diagonal form in the basis of the total angular momentum given by

Here j = 0 (1/2), …, n/2 if n is even (odd), is the identity in the multiplicity space , of dimension (the multiplicity of the representation with total angular momentum j), where

The normalized state ρj, which is supported on the representation subspace of dimension 2j + 1 = d2j, is

where

so that and we stick to our shorthand notation [·] ≡ |·〉〈·|, i.e., [j, m] ≡ |j,m〉〈j,m|. The measurement on defined by the set of projectors on the various subspaces will produce ρj as a posterior state with probability

One can easily check that .

In the large n limit, we can replace for a continuous probability distribution pn(x) in [0, 1], where x = 2j/n. Applying Stirling's approximation to pj one obtains:

where H(s || t) is the (binary) relative entropy

The approximation is valid for x and r both in the open unit interval (0, 1). For non-vanishing r, pn(x) becomes a Dirac delta function peaked at x = r, p∞(x) = δ(x − r), which corresponds to j = nr/2.

Covariance and structure of

We start with a POVM element of the form . Since Dµ must be a rank-one projector, it can always be written as for a suitable SU(2) rotation uµ. Thus,

We next use the invariance of the Haar measure du to make the change of variable: u uµ → u′ and, accordingly, . After regrouping terms we have

where we have defined . The POVM element is obtained by replacing [↑] by [↓] in the expressions above. From the POVM condition it immediately follows that , where is the identity on the Hilbert space of the TS, i.e., . Therefore is a covariant POVM. The positive operator Ω is called the seed of the covariant POVM .

Now, let uz(ϕ) be a rotation about the z-axis, which leaves [↑] invariant. By performing the change of variables u → u′uz(ϕ) [and ] in the last equation above, we readily see that Ω and both give the same average operator for any ϕ ∈ [0, 4π). So, its average over ϕ,

can be used as a seed w.l.o.g., where we have dropped the subscript AC to simplify the notation. Such a seed is by construction invariant under the group of rotations about the z-axis (just like [↑]) and, by Schur's lemma, a direct sum of operators with well defined magnetic number. Therefore, in the total angular momentum basis for AC, we can always choose the seed of as

The constrain (8) follows from the POVM condition and Schur's lemma. The result also holds if A and C have different number of copies (provided they add up to 2n). It also holds for mixed states.

Derivation of Eqs. (29) and (33)

Let us start with the general case where ξ = {j, j′}. To obtain we first write Eqs. (27) as the SU(2) group integrals

where is given in Eq. (38), is the mixed state ρ0, Eq. (26), of the qubit B. We next couple A with B (more precisely, their subspaces of angular momentum j) using the Clebsch-Gordan coefficients

The resulting expressions can be easily integrated using Schur lemma. Note that the integrals of crossed terms of the form |j, m〉〈j′, m| will vanish for all j ≠ j′. We readily obtain

where is the projector on and . The superscripts attached to the various projectors specify the subsystems to which they refer. These projectors are formally equal to those used in Eq. (2) (i.e., projects on the fully symmetric subspace of 2j qubits) and, hence, we stick to the same notation. Note that , as it should be.

We can further simplify this expression by introducing , i.e., the expectation value of the z-component of the total angular momentum in the state ρj (i.e., of in the state ) for a Bloch vector rz:

Using the relation

and (j + 1)/d2j+1 = j/d2j−1 = 1/2, we can write

Similarly, we can show that

Therefore, if j′ = j,

Comparing with Eq. (2), the two terms in the second line can be understood as the average states for a number of 2j pure qubits, i.e., as and respectively. Hence, if ξ = {j,j} we have the relation

which is Eq. (29). It is important to emphasize that this equation is exact (i.e., it holds for any value of j, n and r) and bears no relation whatsoever to measurements (i.e., it is an algebraic identity between the various operators involved).

In the asymptotic limit, for nA and nC of the form , n ≫ 1, a < 1, the probabilities and are peaked at and , as was explained above. Hence, only the average state components with ξ = {j, j′} such that and are important. From Eqs. (50) and (51) it is straightforward to obtain

where we have used that19 up to exponentially vanishing terms. This relation, for the particular value of a = 1/2, is used in the proof of robustness, Eq. (33).

Calculation of Γ↑

Here we calculate , where the average states are defined in Eqs. (27) and explicitly given in Eqs. (50) and (51) for ξ = {j, j′}. Let us first calculate the conditional state . For that, we need to express in the original product basis . Recalling the Clebsch-Gordan coefficients , one readily obtains

which can be written as

where is the z component of the total angular momentum operator acting on subsystem A. An analogous expression is obtained for . Substituting in Eqs. (50) and (51) and subtracting the resulting expressions, one has , with

where we have written ξ = {jA,jC}, instead of ξ = {j,j′} used in the derivation. For pure states, r = 1, jA = jC = n/2, and we recover Eq. (11).

In order to minimize the excess risk using SDP, we find it convenient to write Eq. (9) in the form

where we recall that m = mAC = mA + mC and we assumed w.l.o.g. that the seed of the optimal POVM has the block form . The POVM condition, Eq. (8) must now hold on each block, thus for ξ = {jA,jC}, we must impose that