Introduction

Since the field of nonlinear optics was established by Bloembergen et al.1,2, as nonlinear optical processes are intrinsically inefficient, one of the core challenges within this field has been how nonlinear optical phenomena excited at each point in space can be coherently accumulated (phase-matched) over a long interaction length. Previous research has established a variety of phase-matching technologies, including use of the birefringence properties of crystals3,4 and implementation of periodic structure in a medium (quasi-phase-matching, QPM)1,2,5,6. These achievements have defined a route for applying nonlinear optics to practical uses, including industrial applications such as laser processing and biomedical lasers.

Over the past two decades, a variety of methods, in which engineered functions are incorporated into nonlinear optical processes, have been investigated to begin this new chapter of nonlinear optics. Such methods include QPM techniques that incorporate a variety of periodic7,8,9 or non-periodic structures10,11,12,13 for operating more than two nonlinear optical processes within a single device, and gas-filled hollow-core fibers or photonic crystal fibers in which refractive index dispersions are designed to enhance a specific wavelength region in high-harmonic14,15 or supercontinuum generation16. Also, an angled-beam geometry in two dimensions has been numerically investigated to manipulate a broad Raman generation in solid hydrogen17. Three-dimensional photonic crystals including a metamaterial as a constituent element have also been investigated to engineer nonlinearly converted radiations into a variety of specific emitted directions in which the reciprocal lattice vectors assist in phase matching18,19. Furthermore, other techniques involve zero-index materials that enable phase-matching-free nonlinear optical processes in all directions, demonstrating simultaneous forward and backward four-wave mixings20,21,22. The common conceptual idea among all these methods is that each realizes a specific function by implementing an additional design in a coherent accumulation (phase-matching) process of nonlinear optical phenomena (Fig. 1a).

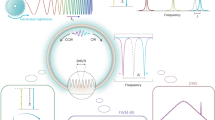
Fig. 1: Conceptual illustrations of the engineered Raman-resonant four-wave-mixing (Rr-FWM) process.
figure 1

Conceptual comparison between engineerings in nonlinear optical processes: a manipulation of the spatial phases, k(ω, r). b Manipulation of relative phases, ϕ(ω, r). c Schematics: the apparatus is a gas cell filled with gaseous para-hydrogen and cooled to 77 K by liquid nitrogen. Six dispersive plates (fused silica) are inserted in the interaction region, where the relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), are manipulated by precise control of the effective optical thicknesses of the plates. d Scheme of the adiabatic excitation of the vibrational coherence, \({\rho }_{ab}\), at a pure vibrational Raman transition of \(\left|{\nu }^{{\prime} {\prime} }=1\right\rangle \leftarrow |{\nu }^{{\prime} }=0{\rangle }\). e Scheme of the high-order Rr-FWM process initiated by laser radiation, \({\varOmega }_{0}^{{{{{{\rm{T}}}}}}}\). The relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), dominate the photon flow between the adjacent Raman modes, \({\varOmega }_{q}^{{{{{{\rm{T}}}}}}}\) and \({\varOmega }_{q-1}^{{{{{{\rm{T}}}}}}}\) . f–i Expected high-order Stokes and anti-Stokes generations in the engineered Rr-FWM processes by manipulating the relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\); f no manipulation applied; g, h output energy accumulations onto a specific Raman mode; and i broad comb-like generation.

Full size image

In contrast, there is another approach to incorporate engineered functions into nonlinear optical processes in which we directly manipulate the scheme of the nonlinear optical process itself by manipulating the phase relationships among the relevant electromagnetic fields (Fig. 1b). This approach has not been extensively studied so far, although it has been described in the expression of the nonlinear optical process itself since the birth of nonlinear optics that nonlinear optical processes are intrinsically affected by the phase relationships among the relevant electromagnetic fields. This approach is more direct and designable in respect of engineering nonlinear optical processes. In fact, on the basis of the concept in Fig. 1b, Zheng and Katsuragawa23 theoretically and numerically showed that a high-order Raman-resonant four-wave-mixing (Rr-FWM) process was tailored to a variety of targets, leading to a single-frequency tunable laser entirely covering the vacuum ultraviolet (VUV) region from 120 to 200 nm as being one of the attractive applications. Furthermore, Ohae et al.24 experimentally demonstrated that the Rr-FWM process in gaseous para-hydrogen was tailored on the basis of this concept.

Here, we again focus on the Rr-FWM process as a representative nonlinear optical process in investigating the concept in Fig. 1b. Although Ohae et al.24 demonstrated the concept, the efficiencies of the Rr-FWM generation were on the order of 10−3, thus limiting the Rr-FWM process to first Stokes and first anti-Stokes generation, as the experiment was executed at room temperature (non-optimal) owing to a technical limitation. To overcome this limitation, we develop a Raman cell system (Fig. 1c) that can arbitrarily manipulate the phase relationships among the relevant electromagnetic fields at a variety of interaction lengths in a nonlinear optical medium held at the liquid nitrogen temperature (optimal). By realizing this Raman cell system, we experimentally tailor the Rr-FWM process with efficiencies of tens of percentages to a variety of targets; namely, we demonstrate accumulation of the output energy to a selected single-Raman mode on demand; and at the opposite extreme, an equal distribution of output energy over high-order Raman modes in the form of a frequency comb. These results are also well reproduced in a numerical calculation and are discussed in respect of the physical mechanism.

Results and discussion

Phase-engineered Raman-resonant four-wave-mixing process

First, we describe the theoretical framework by which the high-order Rr-FWM process can be engineered by implementing the relative phase manipulations during its evolution. Figure 1d, e represents a Rr-FWM process. In this process, a high-Raman coherence, \({\rho }_{{ab}}\), is adiabatically driven by precisely controlling the two-photon detuning, δ, where a pair of long-pulse laser fields at the two wavelengths, Ω0 and Ω−1 are applied25,26,27,28,29. The produced molecular ensemble with high-Raman-coherence functions as an ultra-high-frequency phase modulator and thereby deeply modulates a variety of arbitrary incident laser radiations, \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\)28,29,30. This optical process simultaneously generates a substantial magnitude of high-order Rr-FWM radiations (high-order Stokes, \({\Omega }_{-q}^{{{{{{\rm{T}}}}}}}\), and anti-Stokes, \({\Omega }_{+q}^{{{{{{\rm{T}}}}}}}\), modes) coaxially along the incident laser beam, \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\), without being restricted by angle phase matching.

Maxwell–Bloch equation

A standard framework for the Maxwell–Bloch equation well describes this Rr-FWM process (see Methods). Equation 1 represents one of the coupled propagation equations, expressing the generation of the qth Raman mode, \({\Omega }_{q}^{{{{{{\rm{T}}}}}}}\).

$$\frac{\partial \sqrt{{n}_{q}^{{{{{{\rm{T}}}}}}}}}{\partial z}=\, \frac{N{{\hslash }}{{|}}{\rho }_{{ab}}{{|}}}{{\varepsilon }_{0}c}\left[{d}_{q-1}\sqrt{{\omega }_{q-1}^{{{{{{\rm{T}}}}}}}{\omega }_{q}^{{{{{{\rm{T}}}}}}}}\,{{\sin }}\left(\triangle {\phi }_{q}^{{{{{{\rm{T}}}}}}}\right)\sqrt{{n}_{q-1}^{{{{{{\rm{T}}}}}}}}\right.\\ \left. -{d}_{q}^{* }\sqrt{{\omega }_{q}^{{{{{{\rm{T}}}}}}}{\omega }_{q+1}^{{{{{{\rm{T}}}}}}}}\,{{\sin }}\left({\triangle \phi }_{q+1}^{{{{{{\rm{T}}}}}}}\right)\sqrt{{n}_{q+1}^{{{{{{\rm{T}}}}}}}}\right]$$
(1)

To clearly visualize the role of the relative phase, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), in this nonlinear optical process, we used the following expressions:

$${{{\mbox{E}}}}_{q}^{{{{{{\rm{T}}}}}}}=\frac{\sqrt{{{\hslash }}{\omega }_{q}^{{{{{{\rm{T}}}}}}}}}{{\varepsilon }_{0}}\sqrt{{n}_{q}^{{{{{{\rm{T}}}}}}}}\,{{\exp }}\left(i{\phi }_{q}^{{{{{{\rm{T}}}}}}}\right)$$
(2)
$${\rho }_{{ab}}=\left|{\rho }_{{ab}}\right|{{\exp }}\left(i{\phi }_{\rho }\right)$$
(3)

where \({\phi }_{q}^{{{{{{\rm{T}}}}}}}\) and \({\phi }_{\rho }\) represent the phases of the electric-field amplitude at the qth mode, \({E}_{q}^{{{{{{\rm{T}}}}}}}\), and the Raman coherence, \({\rho }_{{ab}}\), respectively. Then, the relative phase, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), is defined as:

$${\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\equiv {\phi }_{q}^{{{{{{\rm{T}}}}}}}-{\phi }_{q-1}^{{{{{{\rm{T}}}}}}}+{\phi }_{\rho }$$
(4)

Other terms \({n}_{q}^{{{{{{\rm{T}}}}}}}\) and \({\omega }_{q}^{{{{{{\rm{T}}}}}}}\) denote the photon number density and the angular frequency at \({\Omega }_{q}^{{{{{{\rm{T}}}}}}}\), respectively; \({d}_{q}^{{{{{{\rm{T}}}}}}}\) is a coupling coefficient between modes \({\Omega }_{q}^{{{{{{\rm{T}}}}}}}\) and \({\Omega }_{q+1}^{{{{{{\rm{T}}}}}}}\); \(z\) is the interaction length; N is the medium density; \(\hslash\) is the reduced Planck constant; \({\varepsilon }_{0}\) is the vacuum permittivity; \(c\) is the speed of light.

The first term on the right-hand side of Eq. 1 implies energy flows of electromagnetic fields from \({\Omega }_{q-1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{q}^{{{{{{\rm{T}}}}}}}\) and the second term from \({\Omega }_{q+1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{q}^{{{{{{\rm{T}}}}}}}\). According to the signs of the relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\) and \({\Delta \phi }_{q+1}^{{{{{{\rm{T}}}}}}}\), directions of such energy flow change, and their speeds vary depending on their values over a full dynamic range of −π to +π. Therefore, we can tailor the obtained nonlinear optical phenomenon toward a variety of targets by providing the freedom of arbitrarily manipulating the directions of these energy flows including their flow speeds at a variety of interaction lengths desired in the evolution of this phenomenon (Fig. 1f–i).

On-demand phase manipulation among many discrete spectral modes

To implement such phase manipulations in a nonlinear optical medium, it is important to determine how to practically realize such a physical mechanism that can simultaneously manipulate many relevant phases among the high-order Raman modes to arbitrary values. Previous work showed that a simple device with which the optical thickness of a transparent dispersive plate can be precisely tuned over a relatively large plate thickness can manipulate the relative phases among many discrete spectral modes nearly on demand31,32,33,34. This method includes the solution of the high-order temporal Talbot method as one of the many solutions35. Here, we use this tunable plate thickness technology to arbitrarily manipulate the concerned relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\) (Fig. 1c).

Experimental

We developed a Raman cell where six transparent dispersive plates (fused silica with a thickness of 5 mm) were installed in a nonlinear optical medium that was refrigerated down to a liquid nitrogen temperature of 77 K. The effective optical thickness of each plate was electronically controlled by adjusting the incident angle from outside the cell (Fig. 1c) to arbitrarily manipulate the relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\). We used gaseous para-hydrogen (purity > 99.9%) as a nonlinear optical medium with a density controlled at 4.2 × 1019 cm−3 at a temperature of 77 K (Lamb–Dicke regime; experimentally found), providing the smallest inhomogeneous broadening (<200 MHz) at the pure vibrational Raman transition, \({\nu }^{{\prime} {\prime} }=1\leftarrow {\nu }^{{\prime} }=0\) (124.7460 THz). We generated a pair of single-frequency nanosecond pulsed-laser radiations at 801.0817 nm (\({\Omega }_{0}\)) and 1201.6375 nm (\({\Omega }_{-1}\))33 that overlapped in time and space (pulse duration of 6 ns), softly focused them into the medium (waist diameter of 200 μm), and then adiabatically drove a vibrational coherence, ρab (\(\delta\) = 0.5 GHz). We used the second harmonic, \({\Omega }_{0}^{T}\) (400.5408 nm, 6 ns), of the driving laser radiation, \({\Omega }_{0}\), as the initiation laser for the Rr-FWM process. The initiation laser radiation, \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\), was temporally and spatially overlapped with the driving laser radiations, \({\Omega }_{0}\) and \({\Omega }_{-1}\), and introduced into the medium, where the polarization of \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) was set orthogonal to those of \({\Omega }_{0}\) and \({\Omega }_{-1}\). A series of high-order Stokes and anti-Stokes radiations, \({\Omega }_{-2}^{T}\) (600.8188 nm), \({\Omega }_{-1}^{T}\) (480.6514 nm), \({\Omega }_{+1}^{T}\) (343.3195 nm), \({\Omega }_{+2}^{T}\) (300.4038 nm), \({\Omega }_{+3}^{T}\) (267.0250 nm), was generated via the vibrational coherence, \({\rho }_{ab}\), and was manipulated in a variety of ways by controlling the phase relationships among the high-order Raman modes, \({\Omega }_{q}^{T}\). Then, such high-order Raman radiations, \({\Omega }_{q}^{T}\), were picked out at appropriate interaction lengths in the series evolution process and detected by photodiodes with relatively calibrated sensitivities.

Physical mechanism in engineering the Rr-FWM process

A high vibrational coherence, ρab, was adiabatically driven, and thereby, a series of high-order Stokes and anti-Stokes radiations, \({\Omega }_{\pm 1}^{{{{{{\rm{T}}}}}}}\), \({\Omega }_{\pm 2}^{{{{{{\rm{T}}}}}}}\), …, were generated coaxially without being restricted by angle phase matching.

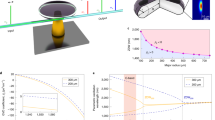
First, we studied how the physical mechanism of the relative phase manipulation implemented in this nonlinear optical process functioned in reality by comparing the resultant Stokes and anti-Stokes generations with those calculated in the numerical simulations. For this purpose, we focused on the generation of the first Stokes and anti-Stokes modes, where only two dispersive plates (A1 and B1 in Fig. 2a) were used. Figure 2b, c shows contour plots of the photon number densities of the generated first Stokes, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) (Fig. 2b), and anti-Stokes, \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\) (Fig. 2c), modes as a function of the angles of the two inserted dispersive plates, A1 and B1, corresponding to manipulations of the effective optical thicknesses (resolution of \({0.015}^{\circ }\), scanning range of \(\pm {7.5}^{\circ }\)). In these plots, 1 represents unity quantum conversion efficiency.

Fig. 2: Physical mechanism of the engineered Raman-resonant four-wave-mixing (Rr-FWM) process.
figure 2

a Experimental layout for the apparatus used for studying the physical mechanism. The angles of plate A1 (at length Z1 = 45 mm) and plate B1 (at length Z2 = 95 mm) were each precisely adjusted with an angular resolution of \({0.015}^{\circ }\) in a range of \({35\pm 7.5}^{\circ }\). The high-order Stokes and anti-Stokes generations initiated from the laser radiation, \({\varOmega }_{0}^{{{{{{\rm{T}}}}}}}\), were monitored by beam reflection with plate A2 at Z3 (145 mm). Here, Z1, Z2, and Z3 are interaction lengths in gaseous para-hydrogen. b, c Contour plots of the observed photon number densities at b \({\varOmega }_{-1}^{{{{{{\rm{T}}}}}}}\) and c \({\varOmega }_{+1}^{{{{{{\rm{T}}}}}}}\) as a function of the insertion angles of plates A1 and B1. 1 implies unity quantum conversion efficiency. d–g Numerically calculated photon number densities at d \({\varOmega }_{-1}^{{{{{{\rm{T}}}}}}}\) and e \({\varOmega }_{+1}^{{{{{{\rm{T}}}}}}}\) and corresponding relative phases, f \({\Delta \phi }_{-1}^{{{{{{\rm{T}}}}}}}\) and g \({\Delta \phi }_{+1}^{{{{{{\rm{T}}}}}}}\), at each angular condition of plates A1 and B1. The white cross in d indicates the point that maximizes the photon number density at \({\varOmega }_{-1}^{{{{{{\rm{T}}}}}}}\) in this explored range. h–j Relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\) (q = −1, 0, 1), at the condition marked by the white cross in d, manipulated as a function of the interaction length, Z. k–m Photon number density distributions among the Raman modes, \({\varOmega }_{q}^{{{{{{\rm{T}}}}}}}\) (q = −2 to 3), calculated at the conditions marked by the white cross in d. The arrows and their thicknesses respectively show how the signs and magnitudes of the relative phases, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), are manipulated to enlarge the photon number density, \({\varOmega }_{-1}^{{{{{{\rm{T}}}}}}}\), as a function of the interaction length, Z.

Full size image

Enhancement and suppression of the mode densities at \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) and \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\) occurred almost periodically, while on the other hand, their near-maximal densities appeared irregularly. These observed features were well reproduced in the corresponding numerical simulations (Fig. 2d, e), including the appearance rates of the near-maximal densities. That is, the numerical simulations well reproduced the intrinsic physical nature of this engineered nonlinear optical process, although it did not perfectly reproduce all properties, including their absolute values, which should depend on the initial phases and the initial absolute plate thicknesses.

Although it is difficult to measure the phase relationships among the Raman modes, \({\Omega }_{{{{{{\rm{q}}}}}}}^{{{{{{\rm{T}}}}}}}\), in the experiment, especially during the evolution of the nonlinear optical process, we can discern such phase relationships in detail from the numerical calculation, as the numerical simulations well reproduced the intrinsic physical nature of the engineered Rr-FWM process (Fig. 2f, g). The periodic behaviors of the observed mode densities were due mainly to the inversion of the signs of the relative phases, \({\Delta \phi }_{0}^{{{{{{\rm{T}}}}}}}\) or \({\Delta \phi }_{1}^{{{{{{\rm{T}}}}}}}\) (see Eq. 1), and the irregular appearances of the near-maximal densities were caused by more details in which more than three relative phases, −, \({\Delta \phi }_{-1}^{{{{{{\rm{T}}}}}}}\), \({\Delta \phi }_{0}^{{{{{{\rm{T}}}}}}}\), \({\Delta \phi }_{1}^{{{{{{\rm{T}}}}}}}\), − in the case of the Raman mode, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\), were non-negligibly associated with different sign-inversion periodicities with different magnitudes which determine the speeds of the relevant photon flows (see Supplementary Fig. S1 for the details including the high-order Raman modes).

In Fig. 2h–j, we show how the relative-phase relationships among the high-order Raman modes, \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), were manipulated along the interaction length at the point marked by the white cross in Fig. 2d, which denotes that the maximal mode density at \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) was found within the explored range. In Fig. 2k–m, we illustrate the flows of the relevant photon number densities provided by \({\Delta \phi }_{q}^{{{{{{\rm{T}}}}}}}\), revealing that such phase relationships were successfully manipulated at interaction lengths Z1 and Z2 so that the photons were accumulated to form the first Stokes mode, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\). Here, the relative phases, \({\Delta \phi }_{0}^{{{{{{\rm{T}}}}}}}\) and \({\Delta \phi }_{1}^{{{{{{\rm{T}}}}}}}\), were manipulated to have negative signs with large amplitudes; therefore, the photon flows were accelerated from \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) and from \({\Omega }_{1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\), respectively. Although \({\Delta \phi }_{-1}^{{{{{{\rm{T}}}}}}}\) was not optimally manipulated for the purpose of maximizing the mode density at \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\), it was manipulated to have a negligible photon flow from \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\). The photon flows from \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{+3}^{{{{{{\rm{T}}}}}}}\) and manipulations of \({\Delta \phi }_{2}^{{{{{{\rm{T}}}}}}}\) and \({\Delta \phi }_{3}^{{{{{{\rm{T}}}}}}}\) were ignored here, as their mode densities were nearly zero.

Up to this point, we confirmed how the physical mechanism of the relative phase manipulations implemented in nonlinear optical processes can work in reality by comparing the fundamental experiment with the detailed numerical simulation.

Application of the engineered Rr-FWM process

On-demand enhancement of a selected Raman mode

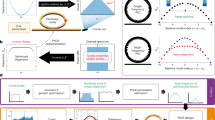
The concept of relative-phase manipulation in nonlinear optical processes has generality; we can apply it to a variety of purposes23. In Fig. 3a–p, we applied such a physical principle to the targets where the output energy in the Rr-FWM process was accumulated to a specific Raman mode selected from the range between the second Stokes mode, \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\), and the second anti-Stokes mode, \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\). For this purpose, we implemented engineered phase manipulations comprising three layers in the Rr-FWM process, each having a pair of transparent dispersive plates, along the interaction length as illustrated in Fig. 3a. The contour plots in Fig. 3b, c are the same as those in Fig. 2b, c. The white cross in each figure indicates the point at which the photon number density (normalized to that at \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\)) was maximized at the first Stokes mode, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\), in Fig. 3b or the first anti-Stokes mode, \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\), in Fig. 3c in the explored range. We fixed the phase manipulations at these conditions as the optimal solutions in the first layer for the targets aimed at as above.

Fig. 3: Demonstrations of the engineered Raman-resonant four-wave-mixing (Rr-FWM) processes.
figure 3

a Schematic layout of the engineered Rr-FWM process, where the relative-phase manipulations comprised three layers, each consisting of a pair of dispersive plates; 1st: A1 (Z1 = 45 mm), B1 (Z2 = 95 mm); 2nd: A2 (Z3 = 145 mm), B2 (Z4 = 195 mm); 3rd: A3 (Z5 = 245 mm), B3 (Z6 = 295 mm). b–k Contour plots of photon number density for each of the Raman modes, \({\varOmega }_{-2}^{{{{{{\rm{T}}}}}}}\) to \({\varOmega }_{+2}^{{{{{{\rm{T}}}}}}}\), observed after each of the three relative-phase manipulation layers (1st, b, c; 2nd, d–g; 3rd, h–k). The crosses in the contour plots indicate the optimal conditions explored in each of the three layers in each of the targets, which maximize a specific Raman mode density of \({\varOmega }_{-2}^{{{{{{\rm{T}}}}}}}\) to \({\varOmega }_{+2}^{{{{{{\rm{T}}}}}}}\). l–p Photon number density distributions among the Raman modes, \({\varOmega }_{q}^{{{{{{\rm{T}}}}}}}\) (q = −2 to 3; \({\varOmega }_{-2}^{{{{{{\rm{T}}}}}}}\): 600.8188 nm, \({\varOmega }_{-1}^{{{{{{\rm{T}}}}}}}\): 480.6514 nm, \({\varOmega }_{0}^{{{{{{\rm{T}}}}}}}\): 400.5408 nm, \({\varOmega }_{+1}^{{{{{{\rm{T}}}}}}}\): 343.3195 nm, \({\varOmega }_{+2}^{{{{{{\rm{T}}}}}}}\): 300.4038 nm, \({\varOmega }_{+3}^{{{{{{\rm{T}}}}}}}\): 267.0250 nm), which were finally achieved at the apparatus exit; for l, no manipulation was applied; for m–p, the plates were engineered towards each of the targets to maximize a specific Raman mode density (red bars) from \({\varOmega }_{-2}^{{{{{{\rm{T}}}}}}}\) to \({\varOmega }_{+2}^{{{{{{\rm{T}}}}}}}\). The overlaid light red bars show the photon number densities calculated by the numerical simulations. q–t Generation of an equal photon number density distribution over broad high-order Raman modes, \({\varOmega }_{-2}^{{{{{{\rm{T}}}}}}}\) to \({\varOmega }_{+2}^{{{{{{\rm{T}}}}}}}\), was examined. The measurements were conducted at four interaction lengths of Z1 (q), Z3 (r), Z5 (s), and Z7 (t) at the exit of the cell. This target was regarded as an opposite extreme to those executed in m–p. Each of the error bars in l–t implies a standard deviation in one hundred measurements executed for each of the Raman mode densities.

Full size image

Next, we moved to the second layer (Fig. 3d–g). Here, also by using two dispersive plates, A2 and B2, we engineered photon flows to extend them to each of the four Raman modes, \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\), from the optimal solutions in the first layer and maximized each of the four Raman mode densities, \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\) in Fig. 3d, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) in Fig. 3e, \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\) in Fig. 3f, and \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\) in Fig. 3g. In Fig. 3d, we substantially enlarged the magnitude of the photon flow to the mode \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\) from \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) (maximized in Fig. 3b). We also simultaneously enhanced the photon flows to \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) from \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) and to \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) from \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\). Conversely, in Fig. 3g, the directions of such photon flows were manipulated to be the opposite; that is, we enlarged the photon flows from \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\), \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\), and \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) to \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\). In Fig. 3e, f, we again implemented the same manipulations as in the first layer. The white crosses in Fig. 3d–g indicate the conditions that maximized the photon number densities for each of the four Raman modes in the explored range, which were then fixed as the optimal solutions at the second layer.

Finally, in the third layer, we repeated the same conceptual phase manipulations as those implemented in the second layer, with the two dispersive plates, A3 and B3, then, we completed this output energy accumulation onto each of the four Raman modes in the Rr-FWM process. The white crosses in Fig. 3h–k indicate the optimal solutions, which indicated the conditions for obtaining maximal photon number densities in the final layer: \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\) in Fig. 3h, \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\) in Fig. 3i, \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\) in Fig. 3j, and \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\) in Fig. 3k.

Figure 3m–p shows the photon number density distributions among the Raman modes that were ultimately achieved through this phase engineering process. When no manipulation was applied (Fig. 3l; dispersive plates not inserted), this nonlinear optical process intrinsically evolved to broaden both the positive and negative high-order Raman modes. Here, by implementing the three relative-phase manipulation layers in the Rr-FWM process, we achieved significant enhancements of specific single-Raman-mode densities: \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\): 0.22\(\pm 0.01\) (no manipulation (nom: 0.047), \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\): 0.50\(\pm 0.03\) (nom: 0.18), \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\): 0.50\(\pm 0.02\) (nom: 0.13), and \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\): 0.29\(\pm 0.02\) (nom: 0.038). The light red bars overlaid in Fig. 3m–p show the mode densities at the targets, simulated numerically with the optimal phase manipulations.

Generation of broad comb-like Raman modes

As already described, the physical concept of the engineered nonlinear optical process described here can be applied for a variety of purposes. In Fig. 3q–t, we examined another target that is regarded as an opposite extreme against those executed in Fig. 3m–p, showing the generation of an equal photon number density distribution over broad high-order Raman modes. Compared with the no-manipulation scenario in Fig. 3l, a very flat photon number density distribution in the form of a frequency comb was realized via the same three layers of relative-phase manipulations: \({\Omega }_{-2}^{{{{{{\rm{T}}}}}}}\): 0.19\(\pm 0.02\), \({\Omega }_{-1}^{{{{{{\rm{T}}}}}}}\): 0.19\(\pm 0.02\), \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\): 0.22\(\pm 0.01\), \({\Omega }_{+1}^{{{{{{\rm{T}}}}}}}\): 0.17\(\pm 0.01\), \({\Omega }_{+2}^{{{{{{\rm{T}}}}}}}\): 0.14\(\pm 0.01\), and \({\Omega }_{+3}^{{{{{{\rm{T}}}}}}}\): 0.10\(\pm 0.01\). The produced spectrum was phase coherent in time and space33, having an ability to generate ultrafast pulses with a temporal duration of 1.2 fs at an ultrafast repetition rate of 125 THz (inset in Fig. 3t).

Discussion on the conceptual differences from related studies

Last, we briefly comment on the conceptual differences between previous studies and the work we present here. In the terminology of adaptive optics, a large number of studies involving the control of nonlinear optical phenomena have been reported. The key concept in such works is the implementation of an artificial design in the distributions of amplitude, phase, or polarization of the incident light to achieve the optimal solution for a specific target, where the feedback control is applied to the light at the incidence and the light-matter interaction is, in general, considered a black box36,37,38,39. Recently, Tzang et al. demonstrated the manipulation of a multimode stimulated Raman scattering cascade in a multimode fiber by applying adaptive-optic control to the wavefront of the incident light, where the angle phase-matching conditions were substantially shaped40. In addition, the conceptual idea of metamaterial: designing optical susceptibility tensors including their phases by creating artificial structures at the nanoscale, has been extended to nonlinear optical processes. Many works on nonlinear beam shaping including the nonlinear optical hologram have been reported41,42,43.

Conclusion

We conducted a proof-of-principle experiment to show that nonlinear processes can be tailored in a variety of ways by manipulating the relative phases among the relevant electromagnetic fields during the evolutions of nonlinear processes. A high-order Rr-FWM process was used as a representative nonlinear process and was tailored to a variety of targets by installing practical phase manipulation devices (thickness-controlled dispersive plates) consisting of three layers in gaseous para-hydrogen controlled in the Lamb–Dicke regime (77 K, 4.2 × 1019 cm−3). We showed that a specific, intentionally selected Raman mode was enhanced on demand with a maximum photon number density of 0.5. We also demonstrated that at the opposite extreme, the photon number densities were equally distributed over the high-order Raman modes in the form of a frequency comb.

The physical concept described here is simple and has generality, paving the way to avenues for incorporating engineered functions in nonlinear optical processes. An attractive potential application of this technology could be the realization of a single-frequency tunable laser entirely covering the VUV region from 120 to 200 nm, as suggested in a previous study23 where \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\) was set at 210 nm. As the mature single-frequency tuneable solid-state laser technology in the near-infrared region established a major trend in atomic-molecular-optical (AMO) physics leading to the realization of Bose–Einstein condensation from the initiation of laser cooling, if an equivalent laser technology can be established in the VUV region, frontiers in AMO physics, such as the laser cooling of anti-matter (Lyman α: 121.6 nm)44 or optical frequency standards locked at nuclear transitions (Th, 149 nm)45,46, may be deeply explored.

Methods

Lasers and operating conditions

The \({\Omega }_{0}\) laser radiation was generated by an injection-locked nanosecond pulsed Ti:sapphire laser (repetition rate: 10 Hz), with a homemade external-cavity-controlled continuous-wave diode laser (800 nm) as the seed laser. The \({\Omega }_{-1}\) laser radiation was generated by an injection-locked optical parametric oscillator (OPO) followed by an optical parametric amplifier (OPA), with the \({\Omega }_{0}\) laser radiation used as the pump laser radiations for both the OPO and the OPA. A homemade external-cavity-controlled continuous-wave diode laser (1200 nm) was used as the seed laser for the OPO. The third laser radiation, \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\), was generated by taking the second harmonic of the driving laser radiation, \({\Omega }_{0}\). Temporal overlap of the three laser radiations (\({\Omega }_{0},{\Omega }_{-1},\) and \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\)) was very stable (pulse duration: 6 ns), as all of them were provided by the single Ti:sapphire laser system. We also coaxially overlapped the three laser beams and softly focused them into the Raman cell. The beam diameters of the three laser radiations at the waist were set to 220 μm at \(\frac{1}{{e}^{2}}\) for \({\Omega }_{-1}\) and \({\Omega }_{0}\) and to 90 μm at \(\frac{1}{{e}^{2}}\) for \({\Omega }_{0}^{{{{{{\rm{T}}}}}}}\). We set wavelengths of the two driving laser radiations to 1201.6375 nm for \({\Omega }_{-1}\) and 801.0817 nm for \({\Omega }_{0}\), and adiabatically drove the molecular coherence, \({\rho }_{{ab}}\)25,27,28,29,30,33, where the frequency difference of the two driving laser radiations was set so that the two-photon detuning, \({{{{{\rm{\delta }}}}}},\) to the vibrational Raman transition (\(\left|b\right\rangle :\left|{{{{{{\rm{\nu }}}}}}}^{{\prime} {\prime} }=1\right\rangle \leftarrow \left|a\right\rangle :{|}{\nu }^{{\prime} }=0\rangle\)) was optimal (0.5 GHz). The pulse energies of the two driving laser radiations were adjusted to 5.3 mJ for \({\Omega }_{-1}\) and 5.0 mJ for \({\Omega }_{0}\).

Theoretical framework: Maxwell–Bloch equation

The high-order Rr-FWM process can be well described by the standard framework of the Maxwell–Bloch equations. In the far-off resonant \(\varLambda\)-scheme, the entire system can be reduced to a two-level system with an effective Hamiltonian as:

$$\begin{array}{c}{H}_{{{{{{\rm{eff}}}}}}}=-{{\hslash }}\left[\begin{array}{cc}{\Omega }_{{aa}} & {\Omega }_{{ab}}\\ {\Omega }_{{ab}}^{* } & {\Omega }_{{bb}}-\delta \end{array}\right]\end{array},$$
(5)

where \({\Omega }_{{aa}}\) and \({\Omega }_{{bb}}\) are ac Stark shifts for the ground state, \({|a}\rangle\), and the excited state, \({|b}\rangle\), respectively, and \({\Omega }_{{ab}}\) indicates the effective two-photon Rabi frequency. Equation 6 represents the equations of motion in the reduced two-level system with a density matrix formula:

$$\frac{\partial {\rho }_{{aa}}}{\partial \tau } =i\left({\Omega }_{{ab}}{\rho }_{{ab}}^{* }+{\Omega }_{{ab}}^{* }{\rho }_{{ab}}\right)+{\gamma }_{a}{\rho }_{{bb}}\\ \,\frac{\partial {\rho }_{{bb}}}{\partial \tau } =-i\left({\Omega }_{{ab}}{\rho }_{{ab}}^{* }+{\Omega }_{{ab}}^{* }{\rho }_{{ab}}\right)-{\gamma }_{b}{\rho }_{{bb}}\\ \,\frac{\partial {\rho }_{{aa}}}{\partial \tau } =i\left({\Omega }_{{aa}}-{\Omega }_{{bb}}+{{\delta }}+{{{{{\rm{i}}}}}}{{{\gamma }}}_{{{{{{\rm{c}}}}}}}\right){\rho }_{{ab}}+i{\Omega }_{{ab}}\left({\rho }_{{bb}}-{\rho }_{{aa}}\right)$$
(6)

here, \({\rho }_{{aa}}\) and \({\rho }_{{bb}}\) are the populations of the ground state, \({|a}\rangle\), and the excited state, \({|b}\rangle\), respectively, and \({\rho }_{{ab}}\) is coherence associated with the Raman transition between states \({|a}\rangle\) and \({|b}\rangle\). The coefficients \({\gamma }_{a}\), \({\gamma }_{b}\), and \({\gamma }_{c}\) are the decay rates of the populations \({\rho }_{{aa}}\) and \({\rho }_{{bb}}\), and the coherence, \({\rho }_{{ab}}\), respectively.

The coupled propagation equation for the complex electric-field amplitude, \({E}_{q}\) (qth Raman mode), propagating in the z direction, is expressed with the slowly varying envelope approximation as:

$$\frac{\partial {E}_{q}^{{{{{{\rm{T}}}}}}}}{\partial z}=i\frac{N{{\hslash }}{\omega }_{q}^{{{{{{\rm{T}}}}}}}}{{\varepsilon }_{0}c}\left({a}_{q}{\rho }_{{aa}}{E}_{q}^{{{{{{\rm{T}}}}}}}+{b}_{q}{\rho }_{{bb}}{E}_{q}^{{{{{{\rm{T}}}}}}}+{d}_{q-1}{\rho }_{{ab}}^{* }{E}_{q-1}^{{{{{{\rm{T}}}}}}}+{d}_{q}^{* }{\rho }_{{ab}}{E}_{q+1}^{{{{{{\rm{T}}}}}}}\right),$$
(7)

where N is the molecular density of para-hydrogen, \({\omega }_{q}\) is the angular frequency at the qth Raman mode, \(\hslash\) is the reduced Planck constant, and \({\varepsilon }_{0}\) is the vacuum permittivity. Parameters, \({a}_{q}\) and \({b}_{q}\) determine the dispersions of para-hydrogen, and \({d}_{q}\) determines the coupling strength between neighboring Raman modes. To show the role of the relative phase more explicitly, we transformed Eq. 7 to Eqs. 8 and 9,

$$\frac{\partial \sqrt{{n}_{q}^{{{{{{\rm{T}}}}}}}}}{\partial z}=\frac{N{{\hslash }}\left|{\rho }_{{ab}}\right|}{{\varepsilon }_{0}c}\left[{d}_{q-1}\sqrt{{\omega }_{q-1}^{{{{{{\rm{T}}}}}}}{\omega }_{q}^{{{{{{\rm{T}}}}}}}}{\sin }\left(\varDelta {\phi }_{q}^{{{{{{\rm{T}}}}}}}\right)\sqrt{{n}_{q-1}^{{{{{{\rm{T}}}}}}}}-{d}_{q}^{* }\sqrt{{\omega }_{q}^{{{{{{\rm{T}}}}}}}{\omega }_{q+1}^{{{{{{\rm{T}}}}}}}}{\sin }\left(\varDelta {\phi }_{q+1}^{{{{{{\rm{T}}}}}}}\right)\sqrt{{n}_{q+1}^{{{{{{\rm{T}}}}}}}}\right]$$
(8)
$$\frac{\partial {\phi }_{q}^{{{{{{\rm{T}}}}}}}}{\partial z}= \,\frac{N{{\hslash }}\left|{\rho }_{{ab}}\right|}{{\varepsilon }_{0}c}\left[{a}_{q}{\omega }_{q}^{T}\frac{{\rho }_{{aa}}}{\left|{\rho }_{{ab}}\right|}+{b}_{q}{\omega }_{q}^{T}\frac{{\rho }_{{bb}}}{\left|{\rho }_{{ab}}\right|}+{d}_{q-1}\sqrt{{\omega }_{q-1}^{{{{{{\rm{T}}}}}}}{\omega }_{q}^{{{{{{\rm{T}}}}}}}}{{\cos }}\left(\varDelta {\phi }_{q}^{{{{{{\rm{T}}}}}}}\right)\sqrt{\frac{{n}_{q-1}^{{{{{{\rm{T}}}}}}}}{{n}_{q}^{{{{{{\rm{T}}}}}}}}}\right. \\ \left.+{d}_{q-1}\sqrt{{\omega }_{q}^{{{{{{\rm{T}}}}}}}{\omega }_{q+1}^{{{{{{\rm{T}}}}}}}}{{\cos }}\left(\varDelta {\phi }_{q+1}^{{{{{{\rm{T}}}}}}}\right)\sqrt{\frac{{n}_{q+1}^{{{{{{\rm{T}}}}}}}}{{n}_{q}^{{{{{{\rm{T}}}}}}}}}\right],$$
(9)

where the complex electric-field amplitude and molecular coherence are transformed as \({E}_{q}^{{{{{{\rm{T}}}}}}}=\left|{E}_{q}^{{{{{{\rm{T}}}}}}}\right|{e}^{i{\phi }_{q}^{{{{{{\rm{T}}}}}}}}\) and \({\rho }_{{ab}}=\left|{\rho }_{{ab}}\right|{e}^{i{\phi }_{\rho }}\), respectively, by using the expressions of photon number density, \({n}_{q}^{{{{{{\rm{T}}}}}}}\propto \frac{{\left|{E}_{q}^{{{{{{\rm{T}}}}}}}\right|}^{2}}{\hslash {\omega }_{q}}\), and the relative phase, \(\varDelta {\phi }_{q}^{{{{{{\rm{T}}}}}}}\). The relative phases, \(\varDelta {\phi }_{q}^{{{{{{\rm{T}}}}}}}\) and \(\varDelta {\phi }_{q+1}^{{{{{{\rm{T}}}}}}}\) are defined as

$$\begin{array}{c}\varDelta {\phi }_{q}^{{{{{{\rm{T}}}}}}}\equiv {\phi }_{q}^{{{{{{\rm{T}}}}}}}-{\phi }_{q-1}^{{{{{{\rm{T}}}}}}}+{\phi }_{\rho }\end{array},$$
(10)
$$\begin{array}{c}\varDelta {\phi }_{q+1}^{{{{{{\rm{T}}}}}}}\equiv {\phi }_{q+1}^{{{{{{\rm{T}}}}}}}-{\phi }_{q}^{{{{{{\rm{T}}}}}}}+{\phi }_{\rho }\end{array}$$
(11)