Introduction

Understanding the electron dynamics in relativistic laser fields has been of core interest in strong-field physics and inspired numerous key applications such as fast ignition fusion, acceleration of charged particles, and producing bright X-/gamma-ray sources. These advances become strong motivations for developing the 10–100PW high-power laser systems1,2,3,4,5,6. Light intensity is likely to approach 1023−24 W cm−2 in the foreseeable future and promote light–matter interaction to the radiation-dominated regime7 or even the quantum electrodynamics (QED) regime8,9,10. In these regimes, an interest in the unique electron dynamics at extreme laser fields arises, in which electrons are accelerated and radiate photons of considerable energies, such that the recoil force is not negligible. This phenomenon is usually referred to as radiation reaction (RR).

Theoretical attempts were made to account for classical RR, such as the Lorentz–Abraham–Dirac equation11 and the Landau–Lifshitz (LL) equation12, both of which were derived from the assumption of continuous classical radiation. The latter is widely accepted because it resolves the nonphysical runaway solution13. Classical treatment is successful in describing accumulative RR effects. In the QED regime, stochastic radiation of high-energy photons14,15 no longer allows one to treat RR as a continuous effect and the quantum effects become effective. While photon emission and the RR force could lead to profound effects in light–matter interaction, such as electron cooling16,17, energy redistribution18, and anomalous trapping of electrons19,20,21, identifying RR in the QED regime has been challenging due to the insufficient peak laser intensities. A direct approach is to head-on collide a high- intensity laser with an energetic electron beam. The laser field can be boosted by a factor of ~γ (electron gamma factor) in the electron rest frame, so that the QED parameter χ = eℏ|F⋅p|/m3c4 can reach unity22, where Fμν is the electromagnetic tensor and pμ is the electron four-momentum. Considerations based on this scenario have been made to observe classical RR7,16,23,24 and quantum effects25,26,27,28,29, by identifying the signature from either the radiated gamma-photons17,27 or the electron dynamics26,28. For the latter in particular, a quantum “quenching” effect is revealed in the head-on colliding geometry for few-cycle laser pulses26, by which some electrons can radiate zero energy and go through the laser field freely.

In this article, we show that new quantum features in electron dynamics arise in the cross-collision geometry at extreme laser intensities. We noticed that classical RR can form a distinctive barrier that blocks electrons with energy below the barrier and allows electrons with energy beyond to pass. However, in the regime where the classical RR barrier allows for full transmission (reflection), we found that an electron can be reflected (transmitted) due to the quantum nature of its dynamics. Intuitively, an electron transmits through the laser field by emitting a smaller amount of energy than it does classically, as suggested in the quantum “quenching” picture26. However, in the quantum reflection (transmission) mechanism, we see that a considerable portion of electrons are reflected (transmitted) by the laser field, even when they radiate lower energy (more energy) than they do classically. The anomalous behavior can be observed by a proposed experiment that measures the reflected electron signal.

Results

Reflection beyond the classical RR barrier

We examine the electron dynamics by perpendicularly colliding a focused laser beam to a high-energy electron bunch. The tightly focused laser30 is polarized in the x-direction and propagates in the z-direction with a profile of \({\mathbf{E}} = {\mathbf{E}}_0(x,y,z,w_0){\mathrm{cos}}^2(\psi /2N)\). Here w0 is the radius of beam waist, ψ (|ψ| < Nπ) the phase term, and N the pulse length in wavelength that focuses at the origin at t = 0, respectively. We start with the simplest case where monoenergetic electrons are injected in the y = 0 plane. A more realistic electron bunch will be discussed later. The reflection ratio of electrons is evaluated in a large parametric region.

We compare the results between the classical approach and the QED calculation in Fig. 1, where a = 300 and γ0 = 250,400 (2 × 1023 W cm−2, 128 MeV, and 204 MeV) are considered. Here λ = 800 nm, w0 = 2λ, pulse length is 20λ, and a = Eeλ/2πmc2 (E is the laser electric field) is the Lorentz-invariant field strength and γ0mc2 is the electron initial energy. The case of pure Lorentz force (LF) is also included for full comparison. In the parameter range of χ < 1, the electron trajectories are greatly diverged. When the RR effect is excluded, all electrons transmit freely through the laser beam, with minor perturbation in the particle trajectories, as shown in Fig. 1a, b. However, a distinctive behavior arises when the classical RR (LL equation is employed) is turned on. At a fixed laser intensity of 2 × 1023 W cm−2, for γ0 = 250, one sees complete reflection of electrons in the colliding vicinity (Fig. 1c). When we increase the electron energy to γ0 = 400, we find that the picture flips where all electrons transmit through the laser beam (Fig. 1d). The drastically different dynamic behavior by slightly varying the electron energy indicates the presence of a clear threshold between the two sets of parameters, i.e., γ0 = 250 and γ0 = 400. These features vanish when we switch to the QED description (see the “Methods” section). In the classical reflection (γ0 = 250, below threshold) or transmission (γ0 = 400, above threshold) regime, we see that 5 out of 100 of test electrons transmit through the laser field in the former and 4 out of 100 get reflected in the latter, as illustrated in Fig. 1e, f, respectively.

Fig. 1
figure 1

Electron trajectories and reflectance for Lorentz force (LF), Landau–Lifshitz (LL) equation, and quantum electrodynamics (QED) radiation. a–f Electron trajectories in y = 0 plane for the LF (a, b), LL (c, d), and QED (e, f) cases, respectively, where a = 300, γ0 = 250 (a, c, e), and γ0 = 400 (b, d, f). g–i Electron reflectance of different (a, γ0) in each case (LF, LL, and QED), where the blue-squared dots are (300,250) and red-squared dots are (300,400). Reflectance maps are calculated by counting electrons injected from z = −10λ to 10λ

Full size image

This disparity is universal in a large parameter range. We quantize the electron reflectance ratio in the (a, γ0) domain in Fig. 1g–i. When RR is turned off, the only barrier for electrons to overcome is the laser ponderomotive potential. Thus, an electron passes through the laser field freely while its initial energy dominates over the ponderomotive potential. This threshold is perfectly fitted by the criterion γ0~a31,32 in Fig. 1g. The RR effect imposes another barrier for electrons. When the laser amplitude increases, the lowest energy for penetration (red-dashed line in Fig. 1h), namely, the barrier, grows higher than that in the no-RR case (white-dashed line in Fig. 1g). Therefore, one sees a clear and sharp threshold that defines reversed features in the electron reflectance, as shown in Fig. 1c, d.

However, the classical RR barrier smears when viewed in the QED perspective. In the parameter region beyond the barrier where LL allows for total transmission, more than 1% of the electrons still get reflected in QED, as shown by the nonzero reflectance above the red-dashed line in Fig. 1i. Moreover, electrons can tunnel through the beam below the barrier due to quantum behavior, which significantly lowers the reflectance as compared with the LL case.

QED effects: anomalous reflection

The QED effect can be best understood by looking at one electron injected at one fixed position for multiple times. The lowest penetration energy for classical LF and LL (white-solid lines) is definite as shown in Fig. 2a. These two curves coincide with the many-particle modeling in Fig. 1g, i. In the QED picture, we repeat the colliding process for 104 times at each set of (γ0, a), where the reflectance probability is defined by \(\frac{{{\mathrm{reflected}}}}{{{\mathrm{total}}}}\). The reproduced probability map in Fig. 2a shows three distinctive regimes. Below the LF boundary is the forbidden zone where the initial electron energy is too small to overcome the ponderomotive barrier. The LL boundary indicates the definite electron dynamics in the classical picture and deviates the transmission and reflection regions shown in Fig. 1a, d. However, in QED, electron dynamics are stochastic and the reflectance is smeared near the LL boundary. The quantum transmission region lies between the LL and the LF boundaries, which becomes more prominent as χ increases. Beyond the LL boundary is the above-threshold zone, where electron energy dominates the classical barrier. The nonzero reflectance above the LL boundary in QED indicates the quantum reflection that is forbidden by the classical LL equation. It should be noticed that the LL boundary can be modified by quantum correction33. However, these quantum effects can always happen due to the stochastic behavior.

Fig. 2
figure 2

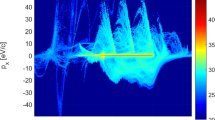
Results of single-electron dynamics for Lorentz force (LF), Landau–Lifshitz (LL) equation, and quantum electrodynamics (QED) radiation. a Electron reflection probability from QED-MC calculation (colormap) when the initial injecting position is fixed at x0 = ct0, z0 = 0 at t = −t0; the white lines are the threshold for classical LL and LF modeling; the dashed line denotes the zero-reflectance threshold for QED. b Histogram of energy loss in QED-MC during t < −1.25T (left), t < −T (middle), and t < 0 (right) for the reflected (blue) and transmitted (red) electrons measured at (a0 = 300, γ0 = 400), where T = λ/c. The energy loss of LL (black-dashed line) is single-valued. c, d Energy loss of the transmitted (red) and reflected (blue) electrons in QED and in LL (black)

Full size image

We further count the radiated energy for each electron in Fig. 2b for a = 300, γ0 = 400 during t < 0, as simulation starts at t = −t0 and the electron is initialized at x0 = ct0, z0 = 0 outside the laser. The LL equation gives a definite single-valued radiated energy at each interaction time. In contrast, energy loss in the QED modeling deviates from the LL equation in several ways. First, QED-MC exhibits a broadened distribution ranging from 0 to 200 MeV due to random radiation, meaning that the electron could lose all the initial energy or radiate nothing. Second, the averaged radiated energy is higher for reflected electrons and lower for transmitted electrons, which is similar to the quantum quenching effect26.

The most interesting feature in Fig. 2b is that some electrons may radiate more (less) than classical calculation, but still transmit (get reflected) as shown by the colored area. These anomalously transmitted/reflected electrons are presented at each colliding phase t = −1.2 T, −1 T, and 0, as recorded in Fig. 2b. The mechanism is further confirmed in Fig. 2c, d by tracking the energy loss of each electron trajectory during collision. These results indicate a new QED feature that has not been revealed previously. Possible electron trajectories are determined by the LL equation or QED; the former contains only one solution for a given condition, while the latter includes various solutions due to the stochastic process, which allows for diverged patterns of radiation and electron trajectories. Therefore, an electron does not necessarily radiate more energy to be reflected or less to transmit. This classically forbidden phenomenon is a most profound reflection of the stochastic quantum laws.

QED effects: angular feature

We consider at a = 350 a more realistic electron bunch of spatial size Δy = Δz = 100λ at the full width at half maximum (FWHM) of the super-Gaussian profile, Δx = 4λ at FWHM of Gaussian profile with E = 102 MeV, 5% energy spread, 10 mrad angular divergence34,35, and peak density of ~1015 cm−3, respectively. We assume electrons located further away from the bunch center to have larger divergence angles with respect to the propagation axis. The relatively large transverse size of the electron bunch can significantly lower down the difficulty of overlapping the bunch and the laser pulse in the cross-collision geometry. The collective plasma field can be neglected due to the very low electron density, such that test particle modeling is sufficient. Otherwise particle-in-cell (PIC) simulations are required.

The results are presented in Fig. 3a, b. The laser pulse drills through the bunch and scatters electrons to large angles. By focusing on the scattered electrons, the measurement is free from the disturbance of background electrons. For long-distance propagation at the order of meter, it is very important to identify the angular distribution after collision. In Fig. 3c, we see clear periodic structures in the LL case, where θ is the polar angle to −x and ϕ the azimuthal angle to z; when we switch to the QED case, such structures vanish in Fig. 3d. In the classical case, there is a specific correlation between the scattering angle and the injected phase, as shown in Fig. 3e. Thus, the oscillation along the scattering angle θ (black horizontal bars) represents the structure of the laser field. However, in the QED case, the scattering angle is no longer single-valued for a certain injecting phase. This is induced by the stochastic effect that allows electrons to enter phases forbidden by the classical model. The broadened scattering angle in QED thus smears the oscillating structure presented in the classical case.

Fig. 3
figure 3

Angular features of the scattered electrons for Landau–Lifshitz (LL) equation and quantum electrodynamics (QED) radiation. a, b Electron density distribution (in log) after cross-collision with a laser for LL (a) and QED (b). c, d Angular distribution of electrons after collision for LL (c) and QED (d). θ is a polar angle to −x axis and ϕ the azimuthal angle to z axis. e Scattering angle θ of test particles initially injected at different phases (or z0) in the y = 0 plane, similar to Fig. 1. Horizontal bars are the electron number records along θ

Full size image

Experimental consideration

One can leverage the new feature to experimentally probe the QED nature at extreme intensities. In this work, we focus on the quantum-reflected electrons as the reflected electron signal is free of the background signal from the abundant transmitted electrons. These effects can be captured experimentally by distributing electron number detectors along θ and ϕ angles and recording the scattered electrons, as shown in Fig. 4a. The records, accumulated from ϕ = −15° to 15° (sections between the dashed lines in Fig. 3c, d) as a function of θ (50 sets of detectors along θ ranging from π/2 to π) are shown in Fig. 4b. Each detector corresponds to an accepting area of ~6 × 6 cm for 2 -m propagation distance. Clear oscillations (spikes and valleys) are reproduced in the detectors along θ in the classical case. This feature is absent in the QED picture, providing an explicit evidence of the QED process. We integrate electron numbers in π/2 < θ < π and obtain the total reflectance at different field strengths in Fig. 4c. The reflection curves show a sharp jump at a = 220 for LL, corresponding to the classical RR barrier. For QED, due to the mechanisms revealed in Fig. 2a, one observes a smoothed transition rather than an abrupt change. We thus conclude that the measurement of electron reflectance along with the angular structure will provide a clear proof of quantum RR.

Fig. 4
figure 4

Illustration of the cross-collision and the results. a Illustration of scattered electrons and detectors based on our numerical results, where the red/blue corresponds to electrons of higher/lower energies. The detector array is placed in the reflection direction to capture the reflected electrons. b Recorded electron number of detectors along θ. c Reflectance of all electrons for different field strengths

Full size image

Discussion

The cross-collision geometry can minimize the electron oscillation times when compared with the head-on collisions, because the current laser systems can focus the spot size to 1 ~ 2λ, but the laser pulse length is usually at about 10λ. To achieve the regime where the QED feature is active, single-cycle or even subcycle laser pulses are required in the head-on collision setup, as shown in ref. 26, which would be very challenging for the state-of-the-art techniques. Cross-collision, on the other hand, is less demanding on the pulse profile to create quantum reflection events. For experimental consideration, the reflected electrons get separated from the electron bunch; i.e., the signal and background are not coaxial, which will be favored for making high-contrast measurements. The critical spatial overlapping/aiming issue in the head-on collision scenario is also mitigated in the cross-collision geometry, where the electron beam can in principle be extended to hundreds of micrometers in diameter, such that the laser pulse can cross it at a picosecond timescale.

Breit–Wheeler pair-production36 in the cross-collision geometry is investigated in a large parameter range with the PIC code SMILEI37. We use the same laser and electron bunch configuration as that in Fig. 3 but in a two-dimensional form. The cell size in the PIC simulations is 0.04λ × 0.04λ with 10 particles per cell. The results are presented in Fig. 5, where the pair-production is strongly suppressed for χ ~ γ ⋅ a ≪ 1. The fraction of the pair-produced electrons is also small when compared with all the reflected electrons. Therefore, we conclude that pair-production does not affect the phenomenon of quantum reflection in the considered parameter space.

Fig. 5
figure 5

Pair-production process in the cross-collision. a Electron-positron pairs produced in the collision. b The fraction of pair-produced electrons for the reflected electrons

Full size image

All the results are calculated with our single-particle model. Here, we compare our results of angular distribution in Fig. 3 with PIC simulation, where the laser and electron bunch configurations in the PIC simulation are the same with the single-particle modeling. The cell size in the PIC simulation is 0.04λ × 0.08λ × 0.08λ with 1 particle per cell, where the first dimension is the laser propagation direction. Comparison of the results is shown in Fig. 6. Although the single-particle modeling ignores the interaction between the electrons, the consistency with each other shows fidelity of our model.

Fig. 6
figure 6

Angular distribution after cross-collision. a, b Single-particle modeling. c, d PIC simulation. a, c are the results of LL equation and b, d are the results of QED radiation

Full size image

In conclusion, we found that perpendicular laser-electron collision provides a unique approach to distinguish the classical and quantum dynamics in the strong-field regime. By calculating the reflectance of injected electrons, we revealed that the classical RR-barrier threshold is not active when viewed in the QED picture. This classical barrier grows to infinity and can block electrons of arbitrarily high energy when the field strength reaches a critical value. In the perspective of QED, electrons may get reflected even when the electron energy goes beyond the classical barrier and transmit for electron energy below the barrier.

We notice that recent experimental efforts have been made to collide laser-wakefield accelerated electrons, with counterpropagating high-intensity laser pulses to produce X-/gamma-rays via Compton scattering38,39,40 and to create RR events41,42. In the former, RR was not active due to relatively low laser intensities. In the experiment by Cole et al.41, the collision probability was limited by the techniques of time synchronization and spatial overlap. Thus, successful events were necessarily identified through extensive theoretical modeling and comparison with experimental results41. In the experiments by Poder et al.42, a more precise model beyond constant cross-field approximation is required to account for the results. Wistisen et al.43 measure the photon spectrum in a positron-crystal collision but did not find a valid theory that fully accounts for the results. We believe that the new QED features of electron dynamics revealed here can be explicitly probed by the measurement proposed in Fig. 4, where the double measurement of the angular structure and the reflectance is self-consistent in identifying the QED effect.

Methods

The classical RR barrier

In a classical picture, we solve the equation of motion dp/dt = FL + FRR numerically for each electron and track their trajectories. Here, FL is the Lorentz force and FRR is the RR force taking the dominating term of LL equation12. In the classical framework, the electron dynamics is deterministic in the sense that it always experiences the same amount of damping if the injection position is constant. We consider an electron initially located at the upper edge of the laser field, as seen in Fig. 7a. The trajectory is presented in the ψ − x space, where ψ = ωt − kz. One notices that before the trajectory turns staggered, there is a depletion zone where it loses the kinetic energy rapidly along a straight line in the space–time domain. This process, namely rapid exhaustion, is the key making electron possible to be reflected by the laser field. For electrons with energy far beyond ponderomotive potential, they must lower down their momenta to a certain level through the rapid exhaustion phase in RR to be reflected by the laser ponderomotive potential.

Fig. 7
figure 7

The classical radiation-reaction barrier. a Electron trajectory in the ψ − x space in a plane laser pulse with a cos2 beam waist w0 = 4λ and peak amplitude a = 400. The electron is initially positioned at z = 0 with γ0 = 104. b The boundary curve from the Landau–Lifshitz (LL) equation transmittance map (circle) and the corresponding results of Eq. (1) (solid), for a different beam size w0 (cyan 3λ, blue 2.5λ, black 2λ, and red 1.5λ) of the Gaussian profile. Dashed lines denote the threshold of the classical LL barrier, namely acr

Full size image

We simplify the geometry to one-dimensional (1D), since the electron moves in the polarization plane and maintains a straight trajectory. To give an explicit formula, the laser is approximated to a plane wave

$$E_x = E_0\,{\mathrm{cos}}\,(kz - \omega t)\,{\mathrm{cos}}^2\left( {\pi x/2w_0} \right)$$

with beam waist w0. Since RR is dominant in the depletion zone, we only consider RR force

$${\mathbf{F}}_{{\mathrm{RR}}} \approx - \frac{{2e^4}}{{3m^2c^4}}\gamma ^2{\mathbf{\beta }}[\left( {{\mathbf{E}} + {\mathbf{\beta }} \times {\mathbf{H}}} \right)^2 - ({\mathbf{E}} \cdot {\mathbf{\beta }})^2]$$

where we only take the dominant term proportional to γ2. We have the rate of energy loss from classical radiation dE/dt = FRR ⋅ v, where vx ≈ −c. Along the straight trajectory, if one has t = (w0 − x)/c then dE/dt only depends on x. Then electron energy evolves as

$$mc^2\frac{{\mathrm{d}\gamma }}{{\mathrm{d}t}} = mc^2\frac{{\mathrm{d}\gamma }}{{\mathrm{d}x}}\frac{1}{{ - c}} = - \frac{{2e^4}}{{3m^2c^3}}\gamma ^2E_x^2(x)\beta _x^2$$

where \(\beta _x^2 \approx 1\). Then we have

$${\int}_{\gamma _0}^{\gamma (x)} {\gamma ^{ - 2}} \mathrm{d}\gamma = {\int}_{w_0}^x {\frac{{2e^4}}{{3m^3c^4}}} E_x^2(x)\mathrm{d}x$$

Finally we obtain the evolution of γ(x) along x

$$\gamma \left( x \right) = \frac{1}{{1/\gamma _0 + a^2{\Bbb I}_{w_0}\left( x \right)}}$$

where \({\Bbb I}_{w_0}(x)\) is an integral relevant to the laser profile. It weakly depends on initial z0, thus, we take z0 = 0 for convenience. From Fig. 7, we see that the depletion zone ends at about w0/4 away from the laser axis, thus, we evaluate the integration \({\Bbb I}_{w_0}(x)\) from x = w0 to w0/4. The lowest energy for an electron to penetrate ponderomotive potential is approximated by demanding γ(w0/4) ~ k ⋅ a, from which we can determine the lowest energy (γ0mc2) to penetrate the laser beam considering a strong RR

$$\gamma _0 = \frac{1}{{1/ka - a^2{\Bbb I}_{w_0}(w_0/4)}}$$
(1)

where k can be determined by the boundary (white-dashed line) in Fig. 1f. Equation (1) depicts the boundary of the classical LL transmittance map. For comparison, we numerically calculate the LL boundary of transmittance in Fig. 2a and compare it with Eq. (1) in Fig. 7b. One sees excellent agreement between the two. For comparison, the w0 of the cos2 profile is scaled to fit the Gaussian profile of the laser in our simulation \(\left( {w_{0,\mathrm{cos}^2} = 1.71w_{0,\mathrm{Gaussian}}} \right)\). Equation (1) reveals the unique LL threshold by setting the denominator to null \(1/ka = a^2{\Bbb I}_{w_0}(w_0/4)\), suggesting an infinite value for the initial electron energy. The critical field strength then scales as

$$a_{{\mathrm{cr}},w_0} = [k\cdot {\Bbb I}_{w_0}(w_0/4)]^{ - 1/3}\sim w_0^{ - 1/3}$$
(2)

where \({\Bbb I}_{w_0}(x)\) is basically linear to w0. Equation (2) reveals the important fact that the LL barrier threshold does not depend on the initial momentum of the colliding electrons. It is only a function of the laser profile. We notice that the scaling of Eq. (2) is consistent with the criteria by which RR dominates over LF44,45 and radiation trapping happens20,21. Particularly, we see that from Eq. (2) that although relevant, the barrier dependence on the laser beam size is relatively weak. Therefore, it is favored by tight focusing of finite laser peak powers, as \(a\sim w_0^{ - 2}\) while \(a_{{\mathrm{cr}},w_0}\sim w_0^{ - 1/3}\).

The QED radiation algorithm

Quantum radiation is treated stochastically, while the motion between the emission events is classical. One can do so because the de Broglie wavelength of an ultra-relativistic electron is much smaller than the optical laser wavelength and the photon formation length mc2/eE~10−3λ is much smaller than the gradient of the field46 in the region we discuss. The emission rate in the QED regime is given in refs. 22,47. We use the synchrotron radiation configuration48,49 based on the solution of a “dressed” electron in external fields; the photon emission is modeled by the synchrotron spectrum50

$$F(\chi ,\delta ) = (1 - \delta )\left[ {y{\int}_y^\infty \mathrm{d} y{\prime}K_{5/3}(y{\prime}) + \frac{{\delta ^2}}{{1 - \delta }}yK_{2/3}(y)} \right]$$

where \(y = \frac{2}{3}\chi ^{ - 1}\frac{\delta }{{1 - \delta }}\) and δ = |F ⋅ ℏk|/|F ⋅ p|≈ℏω/γmc2 represents the photon energy normalized by the electron energy; ℏkμ is four-momentum of the photon. Photon emission is triggered by a modified event generator51 that resolves the cutoff issue in the low-energy region of the radiation model. In the QED-MC algorithm, emission probability and photon energy are determined by two independent random numbers r1 and r2. If r2 < P(r1), a photon of ℏω = r2γmc2 is emitted, where P(r) is the probability density function constructed from F(χ, δ).