Observation of slowly decaying eigenmodes without exceptional points in Floquet dissipative synthetic circuits

Abstrct

Passive parity-time symmetry breaking transitions, where long-lived eigenmodes emerge in a locally dissipative system, have been extensively studied in recent years. Conventional wisdom says that they occur at exceptional points. Here we report the observation of multiple transitions showing the emergence of slowly decaying eigenmodes in a dissipative, Floquet electronic system with synthetic components. Remarkably, in our system, the modes emerge without exceptional points. Our setup uses an electrical oscillator inductively coupled to a dissipative oscillator, where the time-periodic inductive coupling and resistive-heating losses are independently controlled. With a Floquet dissipation, slowly-decaying eigenmodes emerge at vanishingly small dissipation strength in the weak coupling limit. With a moderate Floquet coupling, multiple instances of their emergence and disappearance are observed. With an asymmetric dimer model, we show that these transitions, driven by avoided-level-crossing in purely dissipative systems, are generically present in static and Floquet domains.

Introduction

Over the past decade, systems described by non-Hermitian, parity-time $\left( {{\cal P}{\cal T}} \right)$ symmetric Hamiltonians have become a subject of intense research^1,2. Such a Hamiltonian H_PT is invariant under the combined operations of parity $\left( {\cal P} \right)$ and time-reversal $\left( {\cal T} \right)$, but it does not commute with either of the two. When its non-Hermiticity is small, its eigenvalues λ_k are real and its eigenvectors are simultaneous eigenvectors of the antilinear ${\cal P}{\cal T}$ operator with eigenvalue one. The spectrum changes into complex-conjugate pairs when the non-Hermiticity exceeds a threshold called the ${\cal P}{\cal T}$ symmetry breaking threshold^3,4. At the threshold, two or more eigenvalues of H_PT become degenerate as do the corresponding eigenvectors, i.e., the ${\cal P}{\cal T}$ symmetry breaking point is an exceptional point (EP)⁵. While not fundamental in their origin^6,7,8, such Hamiltonians faithfully describe open classical systems with balanced gain and loss, and have been implemented in photonic lattices^9,10,11,12, microring resonators^13,14,15, superconducting wires¹⁶, and electrical circuits^17,18. In addition to studying the dynamics across the ${\cal P}{\cal T}$ transition, experiments on these systems have observed an enhanced sensitivity ^19,20 and important topological properties²¹ of the EPs, near  the ${\cal P}{\cal T}$ threshold.

When a system has unbalanced gain and loss, the eigenvalues of its non-${\cal P}{\cal T}$-symmetric Hamiltonian are complex and the EP is replaced by an avoided level crossing (ALC)²². ALC refers to the flow of complex eigenvalues towards, and then away from, each other^{23,24,25,26,27,28}. A laser, with its constant cavity loss and a pump-current adjustable gain, is a prototypical system with local, unbalanced gain and loss. Many counter-intuitive transitions such as pump-induced laser death^29,30, loss-induced revival¹³, and self-termination^31,32 in coupled lasers have been observed or predicted, based on the ALC. In all cases, however, the transitions occur when the largest imaginary part of complex eigenvalues changes sign, and system parameters where the ALC occurs, i.e the distance between the eigenvalues in the complex plane is the shortest, do not signal any transition.

Apart from a shift along the imaginary axis, the Hamiltonian for a neutral-loss system is the same as that of a gain-loss system. Thus, the language of ${\cal P}{\cal T}$ symmetry has been adopted to systems with localized dissipation that are “identity-shifted” from a ${\cal P}{\cal T}$ symmetric Hamiltonian³³. When the loss strength γ is small, the equal decay rates of the two eigenmodes of the dissipative Hamiltonian H_D increase with γ. Beyond the threshold, one of the eigenmodes (fast mode) has a rapid decay and the decay rate for the second one (slow mode) decreases with increasing γ. Indeed, the first observation of a passive ${\cal P}{\cal T}$ transition was in a lossy dimer wherein the net transmission increased with the local loss³⁴. In the strictest sense, however, H_D does not commute with the ${\cal P}{\cal T}$ operator, and thus H_D and ${\cal P}{\cal T}$ cannot have simultaneous eigenvectors.

Based on these observations, a passive ${\cal P}{\cal T}$-symmetry breaking transition can be defined as follows. When the local loss is small, the eigenmode decay rates Γ_k≡ − $\Im$λ_k > 0 increase with it. Past a critical value γ_PT, a slowly-decaying mode emerges, whose decay rate Γ_s(γ) decreases when γ is increased further. The passive ${\cal P}{\cal T}$-symmetry breaking threshold γ_PT, then, corresponds to a maximum in Γ_s(γ), i.e.,

$$d{\mathrm{\Gamma }}_{\mathrm{s}}(\gamma _{{\mathrm{PT}}}^ - )/d\gamma > 0{\kern 1pt} \,{\mathrm{and}}\,d{\mathrm{\Gamma }}_{\mathrm{s}}(\gamma _{{\mathrm{PT}}}^ + )/d\gamma < 0,$$

(1)

where $\gamma _{{\mathrm{PT}}}^ \pm$ denotes approaching the threshold γ_PT from the left or right, respectively. For dissipative Hamiltonians that are identity-shifted from H_PT, the emergence of the slow mode is equivalent to the ${\cal P}{\cal T}$ breaking transition of H_PT, and both occur at an EP. However, Eq. (1) also encompasses dissipative Hamiltonians that are not identity shifted from an H_PT and do not have an EP at the threshold γ_PT. The key, experimental signature of “loss-induced transparency”^34,35,36, indicating the emergence of slow-mode, does not depend upon whether it occurs at an EP³⁷. Therefore, we call the region of the parameter-space where the eigenmode decay rates increase with γ as the “${\cal P}{\cal T}$-symmetric” phase and regions where the slowly-decaying eigenmodes exist as “passive ${\cal P}{\cal T}$-symmetry broken” phase.

There is a compelling reason for studying the systems with localized dissipation. The fundamental obstacle to realizing a quantum system with ${\cal P}{\cal T}$-symmetric Hamiltonian is that amplification is accompanied by quantum noise^38,39. In optical settings, at a few-photon level, the gain is randomized by spontaneous emission, while the loss is statistically linear down to a single-photon level. Consequently, there are no realizations of gain-loss systems that show quantum correlations present. A dissipative system, on the other hand, can be implemented down to the quantum level. This approach has led to the observation of passive ${\cal P}{\cal T}$ breaking transitions in the quantum domain with correlated single photons⁴⁰ and a degenerate Fermi gas;⁴¹ in both cases, however, the passive ${\cal P}{\cal T}$ transition occurs at an EP. Equation (1) provides a meaningful way to extend this notion to truly quantum, dissipative systems that do not have an EP.

Here we demonstrate that inductively coupled electronic circuits have the passive ${\cal P}{\cal T}$ symmetry breaking transition in the absence of EPs in both static and Floquet domains. Our system comprises an inductor-capacitor (LC) oscillator inductively coupled to a second one with Joule-heating loss. With static and Floquet versions of the effective, lossy Hamiltonian that describes this system, we characterize the passive ${\cal P}{\cal T}$-symmetric and passive ${\cal P}{\cal T}$-symmetry broken regions, and observe the emergence of slowly decaying eigenmodes that indicate the passive ${\cal P}{\cal T}$ broken region. Finally, by using an asymmetrical dimer model, we show that passive ${\cal P}{\cal T}$ transitions at the ALC occur in both static and Floquet dissipative Hamiltonians. In contrast to the coupled LC circuits with gain and loss^17,18, our system undergoes passive ${\cal P}{\cal T}$ transitions without EPs; it signals an ALC-driven paradigm that is also applicable to a broad array of dissipative quantum systems.

Results

Theory of passive ${\cal P}{\cal T}$ transitions with a static Hamiltonian

Our system is a neutral LC oscillator, formed by a synthetic inductor and capacitor, inductively coupled to another parallel, synthetic, resistive LC (RLC) circuit with a coupling inductor L_x (see Fig. 1a). In parity-time symmetric systems one generally investigates the dynamics of the local density of a quantity ${\cal Q}(t) \equiv \langle \psi (t)|\psi (t)\rangle$ that is conserved when the system is isolated and described by a Hermitian Hamiltonian. For optical ${\cal P}{\cal T}$ systems, ${\cal Q}$ is the total energy in the electromagnetic pulse or, equivalently, the number of photons, and |ψ(t)〉 then represents the location-dependent amplitude of the electric-field envelope; in a passive ${\cal P}{\cal T}$ system with ultracold atoms, ${\cal Q}(t)$ is the total number of atoms in the trap and |ψ(t)〉 is the hyperfine-level associated wavefunction of a single atom. In our case, the time-dependent energy stored in and across the two coupled oscillators is given by a positive-definite quadratic form, i.e., ${\cal Q}(t) \equiv \langle \psi (t)|\psi (t)\rangle = \langle \phi (t)|A|\phi (t)\rangle$. Here A = diag(C, C, L, L, L_x)/2 is a real, diagonal matrix, and |ϕ〉 = (V₁, V₂, I₁, I₂, I_x)^T is a real column-vector comprising the voltages V_1,2 across the two capacitors, the currents I_1,2 across the two inductors, and the current I_x flowing across the coupling inductor. The decay dynamics of the energy ${\cal Q}(t)$ in the system is determined by Kirchhoff laws and leads to a Schrödinger-like equation i∂_t|ψ(t)〉 = H_D|ψ(t)〉 (Methods, Hamiltonian description from Kirchhoff laws). The rank-4, 5 × 5 lossy Hamiltonian is given by

$$H_{\mathrm{D}}(\gamma ) = \left[ {\begin{array}{ccccc} { - i\gamma } & 0 & { - i\omega _0} & 0 & { - i\omega _0M} \\ 0 & 0 & 0 & { - i\omega _0} & {i\omega _0M} \\ {i\omega _0} & 0 & 0 & 0 & 0 \\ 0 & {i\omega _0} & 0 & 0 & 0 \\ {i\omega _0M} & { - i\omega _0M} & 0 & 0 & 0 \end{array}} \right].$$

(2)

Fig. 1

Flow of eigenvalues and transitions in neutral-loss and gain-loss coupled electrical oscillators. a Schematic of an inductor-capacitor (LC) oscillator (gray) inductively coupled to an resistive-LC oscillator (blue). In the weak coupling limit, $M = \sqrt {L/L_x} \ll 1$, this system maps onto a dissipative dimer (Methods, Circuit to dimer mapping). b Flow of eigenvalues $\Re \lambda _k$ as a function of loss shows that the top two (red and blue) levels attract each other and reach a minimum gap ∝M³ near loss strength $\gamma /\omega _0\sim 2M^2$ before diverging again, thus indicating an avoided level crossing (ALC). c Flow of eigenmode decay rates −$\Im$λ_k shows that the slowly decaying modes (blue) emerge at $\gamma /\omega _0\sim 2M^2$ signaling a passive parity-time $\left( {{\cal P}{\cal T}} \right)$ transition at the location of the ALC. The insets show expanded view of the transition region. d Schematic circuit with gain and loss¹⁷. Flows of $\Re \lambda _k$, e, and $\Im$λ_k, f, as a function of the gain-loss strength show that the ${\cal P}{\cal T}$-breaking transition occurs only an exceptional point (EP), γ = (ω_M−ω₀) ∝ ω₀M². The comparison of a and d shows that the transition accompanied by an ALC, instead of an EP, occurs only in the dissipative case

Here, $\omega _0 = 1/\sqrt {LC}$ is the frequency of an isolated oscillator, $M = \sqrt {L/L_x}$ is the dimensionless coupling between the two oscillators, and γ = 1/RC is the dissipation rate of the parallel RLC oscillator. Because this is a classical system, H_D has purely imaginary entries; it ensures that the “state vector” |ψ(t)〉 remains real at all times. Apart from the trivial eigenvalue λ = 0, the characteristic equation for H_D is given by

$$(\lambda ^2 - \omega _0^2)(\lambda ^2 - \omega _M^2) - i\gamma \lambda \left[ {\lambda ^2 - \omega _0^2(1 + M^2)} \right] = 0,$$

(3)

where $\omega _M = \omega _0\sqrt {1 + 2M^2}$. It follows from Eq. (3) that if λ is an eigenvalue of the Hamiltonian H_D, so is −λ^*.

The resulting flow of eigenvalues $\Re \lambda _k(\gamma )$ and $\Im$λ_k(γ) as a function of the dissipation, for M = 0.4, are shown in Fig. 1b,c, respectively. Starting from ±ω₀ (red solid and dot-dashed lines) and ±ω_M (blue solid and dot-dashed lines), the $\Re \lambda _k$ approach each other as γ/ω₀ is increased. The levels reach a minimum gap ∝M³ at loss strength γ/ω₀ ∝ 2M² and then they diverge again, i.e., the static Hamiltonian has an ALC near $\gamma \sim 2M^2\omega _0$. Note that due to this scaling, in the weak coupling limit $M \ll 1$, the gap appears to vanish, just as it does in the balanced gain-loss electrical circuits¹⁷. The inset shows an enlarged view of the transition region. Figure 1c shows the evolution of the doubly-degenerate decay rates Γ_k≡ − $\Im$λ_k. At small dissipation, both (red and blue) decay rates increase with γ. However, at $\gamma /\omega _0\sim 2M^2$, two “slowly decaying” (blue) eigenmodes with dΓ_s/dγ < 0 emerge, indicating a passive ${\cal P}{\cal T}$ symmetry breaking transition which occurs at the location of the ALC. The inset shows an enlarged view of this region, where the shaded part indicates “passive ${\cal P}{\cal T}$ symmetric” region (dΓ_s/dγ > 0) and the unshaded part indicates the “passive ${\cal P}{\cal T}$-symmetry broken” region (dΓ_s/dγ < 0). In contrast, we note that in systems with unbalanced gain and loss^31,32, the interesting physical phenomena^13,30 do not occur at the location of the ALC, but instead at system parameters where max$\Im$λ_k changes sign.

The results for an RLC oscillator coupled to a gain-LC oscillator, Fig. 1d, are shown in the subsequent panels¹⁷. Note that the corresponding Hamiltonian H_PT(γ) is identical to H_D(γ) except for an additional nonzero term given by H_PT(2,2) = +iγ. The resulting flow of $\Re \lambda _k$, Fig. 1e, shows that starting from ±ω₀ (red solid and dot-dashed lines) and ±ω_M (blue solid and dot-dashed lines), the levels for $\Re \lambda _k$ attract each other and become degenerate at the exceptional point γ = ω_M − ω₀. Figure 1f shows that starting from zero, $\Im$λ_k take off in a characteristic square-root pattern at the same EP, i.e. γ = (ω_M − ω₀) ≈ ω₀M². As an aside, we note that both Hamiltonians have an exceptional point deep in the ${\cal P}{\cal T}$ symmetry broken region, at $\gamma /\omega _0\sim 2\sqrt {1 + M^2}$. However, in either case, this EP does not signal any transition.

The results in Fig. 1 predict that in our lossy, static system, a slowly decaying eigenmode emerges at the location of the ALC. When a static, ${\cal P}{\cal T}$-symmetric Hamiltonian is replaced by its Floquet version, a rich phase diagram with multiple ${\cal P}{\cal T}$ transitions with concomitant lines of EPs emerges^42,43,44. How do these results change if we periodically drive a dissipative system that has no exceptional points?

The fate of periodically driven systems, such as children’s swings, has been studied over centuries. The energy dynamics in such a system is either periodic or, near a resonance, unstable in which the energy diverges with time. In real systems, this divergence is saturated by the nonlinearities. Over the past decade, periodically driven quantum systems⁴⁵, i.e., systems with a Floquet Hamiltonian have been extensively investigated^46,47,48. Such a Hamiltonian gives rise to Floquet quasi-energy bands and the time evolution of the system is described by an effective, static Hamiltonian, along with kick operators. Due to its Hermiticity, the time evolution of the system is unitary but the dynamics of energy fluctuations is non-trivial⁴⁹. The energy fluctuations show bounded oscillations at high driving frequencies; at low frequencies, there are “instability regions” where the fluctuations grow exponentially with time until their growth is saturated by the interactions⁴⁹.

In contrast to its Hermitian counterpart, a ${\cal P}{\cal T}$-symmetric Floquet Hamiltonian has complex quasi-energies and non-orthogonal Floquet eigenvectors, and therefore generates a non-unitary time evolution. In this case, the ${\cal P}{\cal T}$ transitions, which always occur at EPs, can be induced by periodically varying the Hermitian part⁴² or the gain-loss part^43,44 of the Hamiltonian in a classical¹⁸ or quantum settings⁴¹. Armed with these insights, we now experimentally investigate the fate of the slowly decaying eigenmodes–which occur without EPs–in the presence of a periodic loss or coupling.

Experimental results for ${\cal P}{\cal T}$ transitions with Floquet loss

We implement a circuit where the resistance in the lossy (RLC) unit is switched between an open circuit and R₀ during a time period T_f ≡ 1/f. The time-periodic, dissipative Hamiltonian in this case is given by Eq. (2) with a square-wave dissipation function, i.e.,

$$\gamma (t) = \left\{ {\begin{array}{*{20}{l}} {\gamma _0} \hfill & {0 \le t \le T_f/4,} \hfill \\ 0 \hfill & {T_f/4 \le t \le 3T_f/4,} \hfill \\ {\gamma _0} \hfill & {3T_f/4 \le t \le T_f.} \hfill \end{array}} \right.$$

(4)

The lossy Hamiltonian H_D is shifted along the imaginary axis from a ${\cal P}{\cal T}$ symmetric Hamiltonian H_PT by a non-identity, diagonal matrix I₂ = diag(1, 1, 0, 0, 0), i.e.

$$H_{\mathrm{D}}(\gamma ) = H_{{\mathrm{PT}}}(\gamma /2) - i\frac{\gamma }{2}{\mathbf{I}}_2.$$

(5)

Since I₂ is not invariant under arbitrary, change-of-basis transformations, H_D(t) and H_PT(t) do not share the same topological structure for their static or Floquet eigenvalue spectra. The ${\cal P}{\cal T}$ phases of the Floquet Hamiltonian H_D(t) are determined by the eigenvalues ν_k of the one-period time-evolution operator $G_{\mathrm{D}}(T_f) = {\mathbf{T}}\,{\mathrm{exp}}\left[ { - i{\int}_0^{T_f} dt\prime H_{\mathrm{D}}(t\prime )} \right]$ where T stands for the time-ordered exponential^50,51. Because we have a piecewise constant Hamiltonian, Eq. (4), the monodromy matrix G_D(T_f) can be explicitly calculated. In addition to the trivial eigenvalue ν = 1, which reflects the rank-4 nature of the 5 × 5 Hamiltonian H_D(t), the remaining eigenvalues ν_k of G_D(T_f) give four dissipative quasienergies λ_k≡lnν_k that also occur in pairs (λ, −λ^*). Thus, there are two distinct, particle-hole symmetric, frequency values $|\Re \lambda _k|$ and two decay rates − $\Im$λ_k > 0 for our system. The passive ${\cal P}{\cal T}$-symmetric phase is signaled by ${\mathrm{\Delta }}\nu \equiv ({\mathrm{max}}|\nu _k| - {\mathrm{min}}|\nu _k|)\sim 0$ and Δν > 0 indicates a passive ${\cal P}{\cal T}$-symmetry broken phase⁵². However, due to the presence of two frequencies and two decay rates that have to be determined from the decaying voltage and current signals, this approach is not experimentally suitable. This is in a stark contrast with the ${\cal P}{\cal T}$-symmetric, Floquet electrical system¹⁸ where only two real parameters are required to characterize either the real quasi-energies (with zero “decay rates”) in the ${\cal P}{\cal T}$ symmetric phase, or a single complex quasi-energy in the ${\cal P}{\cal T}$-broken phase.

An alternate, experimentally friendly approach to track the passive, ${\cal P}{\cal T}$ symmetry breaking transition is to define a scaled energy,

$$E(t) = \langle \psi (0)|G_{\mathrm{D}}^\dagger (t)e^{ + \gamma {\mathbf{I}}_2t}G_{\mathrm{D}}(t)|\psi (0)\rangle .$$

(6)

For a dissipative two-level system, this scaled quantity shows oscillatory behavior in the ${\cal P}{\cal T}$ symmetric phase, with its amplitude and period both diverging as the system approaches the ${\cal P}{\cal T}$ phase boundary, and an exponential rise with time in the ${\cal P}{\cal T}$ symmetry broken phase^33,40,41. This qualitative difference is quantified by the ratio

$$\mu = {\mathrm{log}}\left\{ {\frac{{{\mathrm{max}}\left[ {E\left( {0 \le t \le 2\tau } \right)} \right]}}{{{\mathrm{max}}\left[ {E\left( {0 \le t \le \tau } \right)} \right]}}} \right\},$$

(7)

where τ is an arbitrary (large) time window. When μ = 0, the system is in the passive ${\cal P}{\cal T}$-symmetric phase, while μ > 0 reveals the rate of exponential growth of the scaled energy in the passive ${\cal P}{\cal T}$-broken phase. This procedure provides an operationally straightforward metric to track the transitions between the passive ${\cal P}{\cal T}$-symmetric and passive ${\cal P}{\cal T}$-symmetry broken regions in the two-dimensional parameter space (γ₀, f) of Floquet dissipation.

We experimentally implement the system described in Eqs. (2) and (4) by using functional blocks synthesized with operational amplifiers and passive linear electrical components. (See Methods, Circuit design and parameters, and refs. ^53,54 for details.) Our experimental setup is designed so that the synthetic inductance and capacitance in each oscillator are L = 1 mH and C = 0.1mF, respectively, leading to natural frequency of each oscillator ω₀/2π = 503 s⁻¹. The remaining parameters of the electronic circuit are defined depending on the specific configuration of the system. For the dynamic-dissipation case, the coupling inductor is set to L_x = 8 mH $\left( {M = 1/2\sqrt 2 = 0.35} \right)$ and the resistance is periodically driven by means of an external square-wave signal. The maximum value of the resistance is R_max = 400 Ω, i.e., minγ(t) = 25 s⁻¹. The minimum resistance is selected from R_min = {50, 75, 95, 130, 180} Ω, and gives γ₀ = {200, 133, 105, 77, 56} s⁻¹, respectively. The parallel resistance in the neutral LC circuit is R_N = 1 kΩ and leads to a loss-rate γ_N = 10 s⁻¹ that is far smaller than the loss rate γ(t) in the RLC circuit. In all cases, our time-trace data are take up to t_max = 200 ms, beyond which the effects of the resistor R_N become relevant.

Figure 2a shows that the numerically obtained phase diagram Δν(γ₀, f) has a triangular passive ${\cal P}{\cal T}$-symmetry broken region centered at f = 60 s⁻¹. In its neighborhood, the system is driven from a passive ${\cal P}{\cal T}$-symmetric phase to the passive ${\cal P}{\cal T}$-symmetry broken phase and back at vanishingly small loss-strength by sweeping the frequency f of the Floquet dissipation^43,44. Figure 2b shows that the experimentally friendly ratio μ(γ₀, f), obtained by numerically solving the Kirchhoff-law differential equations (Methods, Hamiltonian description from Kirchhoff laws) and using τ = 40 ms, has the same features. Because of the divergent period of E(t) oscillations near the phase boundary, at a finite τ, points in the passive ${\cal P}{\cal T}$-symmetric regions with period $\gtrsim \tau$ also exhibit a positive ratio μ, and broaden the μ > 0 region in Fig. 2b compared to the Δν > 0 region in Fig. 2a. In both cases, the loss-strength γ₀ is one order of magnitude smaller than the static passive ${\cal P}{\cal T}$-symmetry breaking threshold $\sim 2M^2\omega _0$.

Fig. 2

Observation of Floquet-dissipation induced parity-time (${\cal P}{\cal T}$) transitions without exceptional points. a Phase diagram in the (γ₀,f) plane shows that the passive ${\cal P}{\cal T}$-symmetry broken phase (Δν > 0) occurs at vanishingly small loss strength γ₀ in the vicinity of f = 60 s⁻¹. b Experimentally friendly ratio μ, Eq. (7), shows the same qualitative features, although the μ > 0 region is broadened due to a finite value for the time-scale τ. c Experimentally measured circuit energy ${\cal Q}(t,f)$ traces (red lines) show a clear slowdown of its decay, indicative of the emergence of a slowly decaying eigenmode, in the vicinity of f = 60 s⁻¹ and match well with theoretical predictions (surface plot). The loss strength γ₀ = 77 s⁻¹ is far smaller than the threshold loss strength $\gamma \sim 2M^2\omega _0$ necessary in the static case. d The ratio μ(γ₀,f), obtained from experimental data, shows that the system goes from a passive ${\cal P}{\cal T}$ symmetric region, to the passive ${\cal P}{\cal T}$-symmetry broken region, to a passive ${\cal P}{\cal T}$ symmetric region as the loss-modulation frequency f = 1/T_f is swept (red: data; surface plot: theory). Error bars correspond to 5% deviation from the experimentally measured values

Figure 2c shows the experimentally measured time-traces for the circuit energy ${\cal Q}(t)$ obtained for γ₀ = 77 s⁻¹ and different loss-modulation frequencies f (red lines: data; surface plot: theory). As the modulation frequency is changed from 40 s⁻¹ to 60 s⁻¹, the decay rate for ${\cal Q}(t)$ dramatically slows down and signals the emergence of a slowly decaying mode, i.e., the passive ${\cal P}{\cal T}$-symmetry broken phase. Increasing the modulation frequency further to 80 s⁻¹ drives the system back into the passive ${\cal P}{\cal T}$ symmetric phase. (See Methods, Quantitative analysis of agreement between theory and experiment, for experimental time-traces with additional values of γ₀.) Fig. 2d shows that μ(γ₀, f), obtained from Eq. (7) with τ = 40 ms, changes from zero to maximum as f is swept from 40 s⁻¹ to 60 s⁻¹, and drops back to zero when f is increased further to 80 s⁻¹. The red points are data (with 5% error bars); the surface plot is from theory. The frequency-averaged, time-integrated relative error between theory and experimental results in Fig. 2c is $\delta {\cal Q} = - 0.025 \pm 0.076$ and in Fig. 2d is δμ = 0.0021 ± 0.0017 (Methods, Quantitative analysis of agreement between theory and experiment).

Circuit energy dynamics with moderate Floquet coupling

In this subsection, we experimentally explore the dynamics of circuit energy ${\cal Q}(t)$ when the coupling M(t) is periodically varied. The effective Hamiltonian in this case is given by Eq. (16). In addition to the constant dissipative term, it has a periodic driving term −i∂_tlnM(t) that, on average, does not add or subtract energy from the system. We investigate the emergence of a slowly-decaying eigenmode in this system by tracking the circuit energy ${\cal Q}(t,f)$ and the ratio μ(γ₀, f), when the coupling inductance L_x is varied from L_min = 2 mH (M = 0.707) to L_max = 4 mH (M = 0.5) in a square-wave fashion over a period T_f = 1/f. The values for the static resistance in this configuration are R = {75, 100, 150, 200} Ω, and correspond to loss rates γ = {133, 100, 67, 50} s⁻¹.

Figure 3a shows the numerically obtained phase diagram for the ratio μ(γ,f), where $\mu \sim 0$ indicates a regime where the circuit energy ${\cal Q}(t)$ decays rapidly and the eigenmode decay rates increase with γ (passive ${\cal P}{\cal T}$-symmetric region). In contrast, the regions with μ > 0 denote emergence of a slowly decaying eigenmode (passive ${\cal P}{\cal T}$-symmetry broken region). The experimentally obtained values of the ratio μ are compared with the theoretical predictions in Fig. 3b (red: data, surface: theory). We see that the emergence of the slowly decaying mode near f = 220 s⁻¹ is clearly visible in the data, whereas the other, weaker, peaks are only partially captured. The frequency-averaged, time-integrated relative error between theory and experimental results in Fig. 3b is $\delta {\cal Q} = - 0.038 \pm 0.071$ and δμ = 0.0076 ± 0.027 (Methods, Quantitative analysis of agreement between theory and experiment). The larger error in the Floquet coupling case is a consequence of the instabilities produced by the injection (removal) of energy into (from) the system, which is produced by the periodic changes of the coupling inductance, Eq. (16). These instabilities and resulting parasitic losses become increasingly dominant after half-a-dozen Floquet cycles, and thus limit the time range for reliable data to 2τ ~ 15 ms.

Fig. 3

Decay dynamics of the circuit energy ${\cal Q}(t)$ due to moderate, Floquet coupling. a Numerically computed ratio μ(γ,f), Eq. (7), shows the emergence of slowly decaying modes (μ > 0) at loss strength $\gamma /\omega _0 \ll 1$, most prominently at f = 220 s⁻¹. b Experimentally obtained μ-values capture this mode at f = 220 s⁻¹, and partially capture other, weaker cases of decay slowdown with f ~ {130, 160} s⁻¹ (red: data, surface: theory). The dimensionless coupling $M = \sqrt {L/L_x}$ is varied between M = 0.707 and M = 0.5, and a time-window of τ = 7 ms is used. At longer times $t \gtrsim 2\tau$, instabilities and parasitic losses make the Floquet coupling data unreliable. Error bars correspond to 5% deviation from the experimentally measured values

We note that the multiple emergences of slowly decaying eigenmodes over a small range of coupling modulation frequency is a salient feature of the not-weakly-coupled oscillators. In the weak coupling limit $M \ll 1$, periodic variations of L_x translate into square-wave variation of the effective dimer coupling $J\sim M^2\omega _0/2$ (Methods, Quantitative analysis of agreement between theory and experiment). Such Floquet dimer coupling leads to passive ${\cal P}{\cal T}$-symmetry broken regions at vanishingly small dissipation strength γ₀ only in the neighborhood of resonances 2πf/J = 1,1/2,1/3,…⁴¹. In contrast, results in Fig. 3 demonstrate emergence of slowly decaying eigenmodes at frequencies that are far off the resonance values.

Discussion

In this paper, we have presented the theory and experimental observation of passive ${\cal P}{\cal T}$ symmetry breaking transitions, driven by avoided level crossing, in a dissipative, synthetic circuit with static and time-periodic parameters. We have observed multiple instances of the emergence of slowly decaying eigenmodes at loss strengths that are one order of magnitude smaller than the static threshold loss strength.

Is the phenomenon of a passive ${\cal P}{\cal T}$-symmetry breaking transition, which occurs without an EP and is driven by an ALC, a property singular to our system? Or is it broadly present in dissipative systems that are not “identity shifted” from a balanced gain and loss system? The answer to the latter question is a yes. In the weak coupling limit (M→0,ω₀→∞) the electrical, two-oscillator system maps onto a dimer with tunneling amplitude J = ω₀M²/2 = const. (Methods, Equivalence between quantum and electrical-oscillator systems). When the dissipation in the first oscillator is taken into account, the effective dimer Hamiltonian becomes

$$H_{\mathrm{d}}(t) = - J\sigma _x - \frac{{i\gamma _{\mathrm{d}}(t) + \delta }}{2}(1_2 + \sigma _z).$$

(8)

where σ_k are the Pauli matrices, γ_d(t) = γ(t)/2 is the Floquet loss in one level of the dimer, γ(t) is the square-wave dissipation with a mean-value of γ₀/2, Eq. (4), and the on-site-potential asymmetry δ is present only in the lossy circuit.

When δ = 0 Eq. (8) reduces to the classic case^33,34. Figure 4a shows its decay rates Γ_k as a function of loss strength γ₀ and modulation frequency f. In the static case, i.e., f = 0, (filled red/yellow circles), the decay rates are equal to each other and increase with the loss strength when γ₀/J < 2. The slowly decaying mode (filled red circles) emerges past the passive transition at the EP γ₀ = 2J. In the Floquet case, the surface plots for 0.5 ≤ 2πf/J ≤ 2.5 show that the passive ${\cal P}{\cal T}$ transition occurs at vanishingly small γ₀ when the modulation frequency is near a resonance, i.e., 2πf/J = 2,2/3,…;^41,43,44. The lines of EPs that separate the fast-mode decay-rate surface Γ_F(γ₀, f) and the slow-mode decay-rate surface Γ_s(γ₀, f) are also visible.

Fig. 4

Emergence of fast and slow eigenmodes with or without exceptional points in a dissipative dimer. a Eigenmode decay-rates Γ_F,s for a symmetric dissipative dimer as a function of the loss strength γ₀ and loss modulation frequency f. Results for a static Hamiltonian (filled, red/yellow circles) show a classic bifurcation at the exceptional point (EP) γ₀/J = 2. The Floquet result shows the emergence of a slowly decaying mode at $\gamma _0/J \ll 1$ in the vicinity of resonances 2πf/J = 2,2/3. In this case, the passive parity-time $\left( {{\cal P}{\cal T}} \right)$ transitions occur at EPs. b When the lossy dimer is asymmetric, with δ/J = 0.05, the static result (filled, red/yellow circles) shows unequal decay rates with dΓ/dγ > 0 for small γ₀, leading to slow-mode (filled red circles) for $\gamma _0/J \gtrsim 2$, i.e., at the location of the avoided level crossing (ALC). Floquet results show that a slow mode emerges at $\gamma _0/J \ll 1$ in the vicinity of 2πf/J = 2,2/3. In both static and Floquet cases, the nonzero separation between the two decay rates shows that all passive ${\cal P}{\cal T}$-symmetry breaking transitions in the asymmetric dimer occur at the location of the ALC

Figure 4b shows the results for an asymmetric dimer with δ = 0.05J. In the static case (filled red/yellow circles), the two, slightly unequal decay rates increase with the loss strength, dΓ_k/dγ > 0, when the loss strength is small. That changes for $\gamma /J \gtrsim 2$, where one eigenmode becomes slowly decaying, dΓ_s/dγ < 0 (filled red circles), without an attendant EP. In the Floquet case, the surface plots for decay rates indicate the emergence of a slow mode at $\gamma _0/J \ll 1$ in the vicinity of resonances 2πf/J = 2,2/3,…. However, the nonzero separation between the two surfaces clearly signals that the passive ${\cal P}{\cal T}$ transitions occur at the location of the ALC. The contour lines of the slow-mode decay rate in the (γ₀,f) plane also show that in the vicinity of resonances, Γ_s becomes smaller with increasing loss strength γ₀. In our experiments with Floquet dissipation, the coupling between oscillators is $M = 1/2\sqrt 2 = 0.35$, and the oscillator frequency is ω₀ = 2π × 503 s⁻¹; this gives the dimer tunneling amplitude J = 2π × 30 s⁻¹. Thus, the observed sequence of transitions in the vicinity of f = 60 s⁻¹ in Fig. 2d corresponds to the primary resonance at 2πf/J = 2. Remarkably, ${\cal Q}(t)$ decay dynamics at moderate coupling shows emergence of slowly decaying eigenmodes at multiple frequencies that are not captured by the asymmetric dimer model.

Non-Hermitian degeneracies, exceptional points, and avoided level crossings play an important role in the dynamics of classical, gain-loss ${\cal P}{\cal T}$ symmetric systems. Truly quantum versions of such systems, however, are likely to be of a dissipative nature⁴⁰, and may or may not be “identity shifted” from a balanced gain-loss system. Our results show that in such dissipative systems, the location of the ALC, where the eigenvalue flows are shortest distance apart, is instrumental to the passive ${\cal P}{\cal T}$-symmetry breaking transition. With its versatility, our system provides a starting point for investigating the effects of interaction (nonlinearity), time-delay, and memory - all of which can be implemented via synthetic electronic circuits–on the dynamics of dissipative ${\cal P}{\cal T}$ symmetric systems.

Methods

Hamiltonian description from Kirchhoff laws

The equations of motion for the voltages V_1,2(t) across the two capacitors C, the currents I_1,2(t) across the two inductors L, and the current I_x across the coupling inductor L_x in Fig. 1a are determined by Kirchhoff laws, and are given by

$$\begin{array}{l}\frac{{dV_1}}{{dt}} = - \frac{1}{{RC}}V_1 - \frac{1}{C}I_1 - \frac{1}{C}I_x,\\ \frac{{dV_2}}{{dt}} = - \frac{1}{C}I_2 + \frac{1}{C}I_x,\\ \frac{{dI_1}}{{dt}} = \frac{1}{L}V_1,\\ \frac{{dI_2}}{{dt}} = \frac{1}{L}V_2,\\ \frac{{dI_x}}{{dt}} = \frac{1}{{L_x}}(V_1 - V_2).\end{array}$$

(9)

This set of five linear equations can be written in a matrix form, $i\partial _t|\phi (t)\rangle = \tilde H|\phi (t)\rangle$ where $|\phi \rangle = (V_1,V_2,I_1,I_2,I_x)^T$ is a real column vector, and the purely imaginary, non-symmetric, non-Hermitian matrix $\tilde H$ is

$$\tilde H = i\left[ {\begin{array}{*{20}{c}} { - \frac{1}{{RC}}} & 0 & { - \frac{1}{C}} & 0 & { - \frac{1}{C}} \\ 0 & 0 & 0 & { - \frac{1}{C}} & {\frac{1}{C}} \\ 0 & {\frac{1}{L}} & 0 & 0 & 0 \\ {\frac{1}{{L_x}}} & { - \frac{1}{{L_x}}} & 0 & 0 & 0 \end{array}} \right].$$

(10)

The energy in this circuit is given by

$${\cal Q}(t) = \frac{1}{2}CV_1^2 + \frac{1}{2}CV_2^2 + \frac{1}{2}LI_1^2 + \frac{1}{2}LI_2^2 + \frac{1}{2}L_xI_x^2$$

(11)

and can be represented by a positive quadratic form, i.e., ${\cal Q} = \langle \phi |A|\phi \rangle$ where A = diag(C, C, L, L, L_x)/2 is a diagonal matrix. Defining a new variable |ψ〉 = A^1/2|ϕ〉 with the dimensions of square-root of energy $\left( {\sqrt {{\mathrm{Joule}}} } \right)$, in the static case, the Kirchhoff-law Eq. (9) lead to

$$i\partial _t|\psi (t)\rangle = H_{\mathrm{D}}|\psi (t)\rangle ,$$

(12)

$$H_{\mathrm{D}} \equiv A^{1/2}\tilde HA^{ - 1/2}.$$

(13)

Although $\tilde H$ is not Hermitian in the zero-loss case (1/R = 0), the transformed Hamiltonian matrix H_D, Eq. (2), is Hermitian in that limit (γ = 0). The dissipative Hamiltonian $H_{\mathrm{D}}(\gamma )$ is shifted from its ${\cal P}{\cal T}$ symmetric counterpart by $H_{{\mathrm{PT}}}(\gamma /2) = H_D(\gamma /2) + i(\gamma /2)I_2$. The Hamiltonian H_PT commutes with the ${\cal P}{\cal T}$ operator where the block-diagonal, 5 × 5 parity and time-reversal operators are given by

$${\cal P} = \left( {\begin{array}{*{20}{c}} {\sigma _x} & 0 & 0 \\ 0 & {\sigma _x} & 0 \\ 0 & 0 & { - 1} \end{array}} \right),\quad {\cal T} = \left( {\begin{array}{*{20}{c}} {1_2} & 0 \\ 0 & { - 1_3} \end{array}} \right){\cal K},$$

(14)

where 1_k is a k × k identity matrix, and ${\cal K}$ denotes complex conjugation.

When the circuit parameters are time dependent, the change-of-basis matrix A^1/2(t) may become time dependent as well. In this case, to change from the |ϕ〉 basis to the |ψ〉 = A^1/2(t)|ϕ〉 basis, we have to include the gauge-field term that is generated by the time-dependent change of basis. Taking it into account gives

$$H_{\mathrm{D}}(t) = \sqrt {A(t)} \tilde H(t)\frac{1}{{\sqrt {A(t)} }} - i\sqrt {A(t)} \partial _t\frac{1}{{\sqrt {A(t)} }}.$$

(15)

In the Floquet dissipation case, the change-of-basis matrix is time independent and so the dissipative Hamiltonian $H_{\mathrm{D}}(t) = A^{1/2}\tilde H(t)A^{ - 1/2}$ only has a time-dependent loss rate γ(t) = 1/R(t)C. In the Floquet L_x(t) case, the gauge-field term is nonzero and leads to H_D(t) = 

$$\left[ {\begin{array}{*{20}{c}} { - i\gamma } & 0 & { - i\omega _0} & 0 & { - i\omega _0M(t)} \\ 0 & 0 & 0 & { - i\omega _0} & {i\omega _0M(t)} \\ {i\omega _0} & 0 & 0 & 0 & 0 \\ 0 & {i\omega _0} & 0 & 0 & 0 \\ {i\omega _0M(t)} & { - i\omega _0M(t)} & 0 & 0 & { - i\partial _t\text{ln}M(t)} \end{array}} \right],$$

(16)

where $M(t) = \sqrt {L/L_x(t)}$ characterizes the dimensionless coupling between the lossy oscillator and the neutral oscillator. Equations (13), (15), and (16) thus provide the requisite mapping from the Kirchhoff-laws description to the Hamiltonian description.

Circuit design and parameters

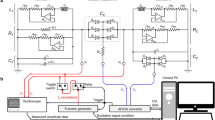
Our experimental setup starts with two identical RLC electrical oscillators coupled by an inductor. The objectives of this work demands versatility in defining the elements used in the oscillators, as well as the coupling, in terms of static and dynamic changes in magnitude. For the static condition, a controllable and fixed value is needed, and for the dynamic case, a precise control in the magnitude, frequency, and phase is required. Additionally, two independent and synchronized clocks are needed as well, one to define the initial conditions and the second to define the demanded dynamic changes. The solution is possible with the help of electronically synthesized circuits, using an analog computer built from different configurations of operational amplifiers^53,54,55.

The problems associated with the faulty contacts and poor stability are resolved by mounting and soldering the electronic components of each oscillator and the coupling on a printed circuit board (PCB). The PCBs are designed in Altium Software and fabricated in a standard chemical etching process. Along these lines, the reproducibility and stability requires components to control offset, drift, and hidden frequency dependence. The implementation includes metal resistors (1% tolerance), polyester capacitors, operational amplifiers (MC1458 and LF353) and analog multipliers (AD633). A stable DC power source is used to energize the electronic circuit, particularly, the 12 V bias voltage for the operational amplifiers.

The voltage signals in the electronic circuit correspond to the physical variables used in the mathematical model. The dynamics of the system are followed by measuring independently the variables of each oscillator (the voltage in the capacitor and the current in the inductor) and the coupling current, i.e., we measure the real, time-dependent vector |ϕ(t)〉. The acquisition of the voltage signals is performed with a Rohde & Schwarz oscilloscope, which has a 12-bits resolution in its analog/digital converter (impedance 1 MΩ), and can transmit directly to a computer through a PC-OSCILLOSCOPE interface, which transfers the information by a USB connection. Each measurement is averaged up to 64 times to reduce the influence of the electronic noise associated to the components.

The initial input energy ${\cal Q}(t = 0)$ is injected into the system using an Arbitrary Waveform Generator (AWG) from Agilent 33,220 A. The signal generated consists of a single pulse with a pulse duration of 0.2 ms and frequency 5 s⁻¹. The high-level voltage amplitude is 5 V, while the low-level voltage amplitude is 0 V. Besides setting the initial conditions, this clock synchronizes the system with the components’ dynamical changes.

To implement the Floquet Hamiltonians, dynamic variations are introduced in the system by means of changes in the desired element of the system. The frequency, phase, and magnitude of the changes are defined by the period, phase, and amplitude of a voltage signal, which is provided by the second AWG from Agilent 33,220 A. The high-voltage and the low-voltage amplitude levels correspond to the high and low energy-dissipation in the resistor, whereas in the case of dynamic coupling, the high level corresponds to a high inductance value, and the low level is related to a low inductance. All experiments are performed using the same PCB. The different configurations are reached by means of three mechanical selectors that remain in place during the course of the experiments.

Quantitative analysis of agreement between theory and experiment

In this section we provide a quantitative analysis of the similarity between our experimental results and the theoretical predictions. For this, first, we focus on the raw data of the experiment, that is, the decaying-energy ${\cal Q}(t)$ directly measured in the circuit, Eq. (11). Figure 5 shows typical energy scans in the time-modulation frequency plane for two different γ₀ values (red lines: data; surface: theory). In each case, we see that the energy decay rate is dramatically lowered at f = 60 s⁻¹ and the relative magnitude of the change is larger for higher loss strength γ₀.

Fig. 5

Dependence of the circuit energy ${\cal Q}(t,f)$ on different loss strengths. When the loss isγ₀ = 200 s⁻¹, a, the slowly decaying mode in the vicinity of f = 60 s⁻¹ is prominent, while for γ₀ = 56 s⁻¹, b, it is visible. In all cases, the data (red lines) match the theory (surface) well

We define a time-averaged relative error for a given loss strength γ₀ and frequency f as

$$\delta {\cal Q}(\gamma _0,f) \equiv 1 - \frac{1}{{2\tau }}{\int}_0^{2\tau } \frac{{{\cal Q}^{{\mathrm{exp}}}(t\prime )}}{{{\cal Q}^{{\mathrm{th}}}(t\prime )}}dt\prime ,$$

(17)

where ${\cal Q}^{{\mathrm{exp}}}(t\prime )$ is the experimentally measured circuit energy and ${\cal Q}^{{\mathrm{th}}}(t\prime )$ is the theoretical prediction for it. The resulting relative error values for the Floquet-loss experimental data are shown in Fig. 6. We also define the relative error in the ratio, Eq. (7), as

$$\delta \mu (\gamma _0) = 1 - \left\langle {\frac{{\mu ^{{\mathrm{exp}}}(\gamma _0,f)}}{{\mu ^{{\mathrm{th}}}(\gamma _0,f)}}} \right\rangle _f,$$

(18)

where 〈…〉_f denotes the average over loss-modulation frequencies.The second and third column in Table 1 show the frequency-averaged $\delta {\cal Q}(\gamma _0)$ and δμ(γ₀) for the experimental data.

Fig. 6

Quantifying the relative error in the circuit energy, $\delta {\cal Q}$, and the ratio, δμ, for Floquet dissipation data. Plots of $\delta {\cal Q}(\gamma _0,f)$ as a function f for different γ₀ show that the error is typically positive in the passive parity-time $\left( {{\cal P}{\cal T}} \right)$ symmetric region and negative in the passive ${\cal P}{\cal T}$-symmetry broken region

Table 1 Frequency-averaged relative error in the Floquet-dissipation circuit energy

Figure 7 and Table 2 show that the relative error in the circuit energy $\delta {\cal Q}(\gamma ,f)$ for the dynamic coupling case is, typically, larger than that in the dynamic dissipation case. This is due to the fact that any change in the coupling between oscillators, represented by the inductor L_x, removes (injects) energy from (into) the system. This creates instabilities in the experimental system, which leads to a larger uncertainty in the measurement of the circuit variables.

Fig. 7

Relative error in the circuit energy $\delta {\cal Q}(\gamma ,f)$ shows that μ > 0 regions correlate with negative $\delta {\cal Q}$, as they do in the Floquet dissipation case, Fig. 6. The time-window used for calculating the ratio μ is τ = 7 ms

Table 2 Frequency-averaged relative error in the Floquet-coupling circuit energy

Circuit to dimer mapping

The dynamics of a single excitation in a system comprising two coupled quantum oscillators is described by the Schrödinger equation

$$i\partial _t\left| {\psi \left( t \right)} \right\rangle = \hat H_{{\mathrm{osc}}}\left| {\psi \left( t \right)} \right\rangle,$$

(19)

where the Hamiltonian $\hat H_{{\mathrm{osc}}}$ is given by

$$\hat H_{{\mathrm{osc}}} = \mathop {\sum}\limits_{n = 1}^2 \varepsilon _n\left| n \right\rangle \left\langle n \right| + \mathop {\sum}\limits_{n \ne m}^2 J_{nm}\left| n \right\rangle \left\langle m \right|,$$

(20)

with |n〉 denoting the energy density at the nth oscillator. The nth-site energies and the coupling between sites n and m are described by ε_n and J_nm, respectively. By expanding the time-dependent wavefunction in the site basis, i.e., $\left| {\psi \left( t \right)} \right\rangle = \mathop {\sum}\nolimits_n c_n\left( t \right)\left| n \right\rangle$, it is easy to find that Eq. (19) leads to a set of coupled equations of first order in the time derivative,

$$i\partial _tc_n = \varepsilon _nc_n\left( t \right) + \mathop {\sum}\limits_{n \ne m}^2 J_{nm}c_m\left( t \right).$$

(21)

In the weak-coupling limit $\left( {J_{nm} \ll \varepsilon _n} \right)$, the time-derivative of Eq. (21) becomes^56,57

$$\partial _t^2c_n + \varepsilon _n^2c_n + \varepsilon _n\mathop {\sum}\limits_{n \ne m}^2 2J_{nm}c_m$$

(22)

Thus, by considering similar oscillators $\left( {\varepsilon = \varepsilon _1 \simeq \varepsilon _2} \right)$, we can define K = 2εJ₁₂ = 2εJ₂₁ = 2εJ and obtain⁵⁶

$$\partial _t^2c_ + + \left( {\varepsilon ^2 + K} \right)c_ + = 0,$$

(23)

$$\partial _t^2c_ - + \left( {\varepsilon ^2 - K} \right)c_ - = 0,$$

(24)

where c_± = c₁ ± c₂ denote the normal modes of the two oscillator system.

To establish a connection between the quantum model and our experimental setup, let us consider Eq. (9) in the non-dissipative limit, that is, when 1/R = 0,

$$\begin{array}{l}\frac{{dV_1}}{{dt}} = - \frac{1}{C}I_1 - \frac{1}{C}I_x,\\ \frac{{dV_2}}{{dt}} = - \frac{1}{C}I_2 + \frac{1}{C}I_x,\\ \frac{{dI_1}}{{dt}} = \frac{1}{L}V_1,\\ \frac{{dI_2}}{{dt}} = \frac{1}{L}V_2,\\ \frac{{dI_x}}{{dt}} = \frac{1}{{L_x}}V_1 - \frac{1}{{L_x}}V_2.\end{array}$$

(25)

It is straightforward to rewrite these equations as⁵⁴

$$\partial _t^2V_ + + \left( {\omega _0^2(1 + M^2) + \omega _0^2M^2} \right)V_ + = 0,$$

(26)

$$\partial _t^2V_ - + \left( {\omega _0^2(1 + M^2) - \omega _0^2M^2} \right)V_ - = 0,$$

(27)

where V_± = V₁ ± V₂ are the symmetric and antisymmetric normal modes of two LC circuits, $\omega _0 = 1/\sqrt {LC}$ is the frequency of an isolated LC circuit, and M² = L/L_x.

By comparing Eqs. (23)–(24) with Eqs. (26)–(27), we find that our experimental setup, in the weak-coupling regime, is equivalent to a quantum-mechanical system by setting c_1,2 → V_1,2, $\varepsilon \to \omega _0\sqrt {1 + M^2}$, and an effective tunneling amplitude

$$J \to \frac{{\omega _0M^2}}{{2\sqrt {1 + M^2} }}.$$

(28)

Thus, the weak-coupling limit can be formally defined by M → 0, ω₀ → ∞ such that the product J = ω₀M²/2 remains constant.