Introduction

Dimension is an important resource in quantum information theory, for instance, a high dimensional quantum system can enhance the performance of the quantum computation1, 2, quantum entanglement3, quantum communication complexity4 and others, and it can also reduce the security of certain practical quantum key distribution systems5. To estimate the lower bound of the dimensions of a physical system, quantum dimension witness has been proposed and experimentally realized6,7,8,9, which has important applications in the semi-device-independent quantum key distribution and quantum random number generation10,11,12,13,14,15. Until now, it has been demonstrated that two-observer classical dimension witness violation can be achieved with the Bell inequality test, quantum random access code test, and determinant value test respectively16,17,18, but whether the multi-observer classical dimension witness violation can be obtained or not is still an open question.

Similar to a quantum dimension witness, quantum nonlocality also plays a fundamental role in quantum information theory, which can be used to guarantee the security of device-independent quantum information protocols19, 20. In a two-observer system, two observers can perform independent measurements on their subsystem to test the Clauser-Horne-Shimony-Holt (CHSH) inequality21, the violation of which certifies quantum nonlocality. Recently, it has been demonstrated that nonlocality sharing among three observers can be established by applying weak measurement technology22,23,24, which demonstrates that subsequent measurements can not be described by using classical probability distributions.

Inspired by the work of sharing nonlocality with weak measurement technology, three-observer classical dimension witness violation will be analyzed in this paper, in which we analyze the dimension witness inequality based on the quantum random access code and the nonlinear determinant value. The analysis result indicate that double classical dimension witness violations can be realized. More interestingly, we demonstrate local and global randomness generation in the three-observer protocol, and the analysis method can also be applied to future multi-observer quantum network studies.

Results

Quantum dimension witness based on quantum random access code

The first quantum dimension witness inequality based on the quantum random access code in the two-observer system is given by10, 11, 18

$$\begin{array}{ccccc}\\ W_1 = & p(1|000) + p(1|001) + p(1|010) - p(1|011)\\ \\ & - p(1|100) + p(1|101) - p(1|110) - p(1|111).\\ \end{array}$$
(1)

In the two-dimensional Hilbert space, it has been proved that the upper bound of the classical dimension witness value W1 is 2, while the upper bound of the quantum dimension witness value W1 is \(2\sqrt 2\). We will apply this dimension witness equation to analyze the dimension witness values between Alice and Bob W1AB and between Alice and Charlie W1AC.

Based on the state preparation and measurement model given in the Method section, the dimension witness value between Alice and Bob is given by

$$W_{1{\mathrm{AB}}} = \sqrt 2 ({\mathrm{cos}}(\epsilon) + 1).$$
(2)

The dimension witness value between Alice and Charlie is given by

$$W_{1{\mathrm{AC}}} = 2\sqrt 2 \mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon).$$
(3)

Note that ε = 0 indicates \(W_{1{\mathrm{AB}}} = 2\sqrt 2\) and W1AC = 0, which demonstrates that Charlie’s quantum state has no interaction with Bob’s system. In this case, only W1AB violates the classical upper bound, which is reduced to a two-observer system (Alice-Bob). Similarly, \(\epsilon = \frac{\pi }{2}\) indicates W1AB = 0 and \(W_{1{\mathrm{AC}}} = 2\sqrt 2\), which is reduced to a two-observer system (Alice-Charlie). Thus, our protocol is more general compared with the previous 2-observer protocols, which sheds new light on the dimension witness in the network environment.

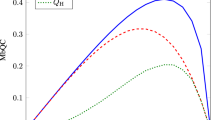
The detailed quantum dimension witness values W1AB and W1AC with different weak measurement parameter ε values are given in Fig. 1. The analysis results indicate that double classical dimension witness violations (min{W1AB,W1AC}>2) can be obtained if the weak measurement parameter ε satisfies \({\mathrm{arcsin}}\left( {\root {4} \of {{\frac{1}{2}}}} \right) < \epsilon < {\mathrm{arccos}}(\sqrt 2 - 1)\).

Fig. 1
figure 1

Three-observer classical dimension witness violation based on the quantum random access code test. ε is the weak measurement parameter. The dashed green line corresponds to the quantum dimension witness value W1AB, solid blue line corresponds to the quantum dimension witness value W1AC, and red area corresponds to the double classical dimension witness violation.

Full size image

Quantum dimension witness based on the determinant value

The second quantum dimension witness inequality based on the nonlinear determinant value test in the two-observer system is given by13, 14

$$W_2 = \left| {\begin{array}{*{20}{c}} {p(1|000) - p(1|010)} & {p(1|100) - p(1|110)} \\ {p(1|001) - p(1|011)} & {p(1|101) - p(1|111)} \end{array}} \right|.$$
(4)

Assuming that the state preparation and measurement devices are independent, it has been proved that this nonlinear dimension witness can tolerate an arbitrarily low detection efficiency. In the two-dimensional Hilbert space, the upper bound of the quantum dimension witness value is 1, while the classical dimension witness value is 0. Similar to the previous subsection, the dimension witness values between Alice and Bob W2AB and between Alice and Charlie W2AC can be analyzed.

Based on the state preparation and measurement model given in the Method section, the dimension witness value between Alice and Bob is given by

$$W_{2{\mathrm{AB}}} = \left( {\frac{1}{2}{\mathrm{cos}}(\epsilon ) + \frac{1}{2}} \right)^2.$$
(5)

The dimension witness value between Alice and Charlie is given by

$$W_{2{\mathrm{AC}}} = \mathop {{{\mathrm{sin}}}}\nolimits^4 (\epsilon ).$$
(6)

Note that ε = 0 indicates W2AB = 1 and W2AC = 0, which demonstrates that Charlie’s quantum state has no interaction with Bob’s system. In this case, only W2AB violates the classical upper bound, which is reduced to a two-observer system (Alice-Bob).

The detailed quantum dimension witness values W2AB and W2AC with different weak measurement parameters ε are given in Fig. 2.

Fig. 2
figure 2

Three-observer classical dimension witness violation based on the determinant value. The dashed green line corresponds to the quantum dimension witness value W2AB, and solid blue line corresponds to the quantum dimension witness value W2AC.

Full size image

The analysis result demonstrates that double classical dimension witness violations (W2AB > 0, W2AC > 0) can be obtained if 0 < ε < π. However, since Bob’s system may be influenced by Alice and Charlie’s system, the security of the measurement outcome b should be guaranteed by considering the double classical dimension witness violation W2AB > 0 and W2AC > 0.

Semi-device-independent random number generator

The classical dimension witness violation can generate semi-device-independent quantum random numbers, for which we can only assume knowledge of the dimension of the underlying physical system, but otherwise nothing about the quantum devices. The generated random numbers in our protocol are the measurement outcomes b and c, and the eavesdropper can not guess the measurement outcomes even if the state preparation and measurement devices are imperfect.

Randomness generation can be divided into global randomness and the local randomness, where global randomness must analyze the global conditional probability distribution p(b,c|x,y,z), while local randomness must analyze the local conditional probability distribution p(b|x,y). With the given conditional probability distributions, the random number generation efficiency can be estimated by following min-entropy functions25

$$\begin{array}{*{20}{c}} {H_{{\mathrm{min1}}} = - \mathop {{{\mathrm{log}}}}\nolimits_2 \left[ {\frac{1}{{16}}\mathop {\sum}\limits_{x,y,z} {\mathrm{max}}_{b,c}(p(b,c|x,y,z))} \right],} \\ {H_{{\mathrm{min2}}} = - \mathop {{{\mathrm{log}}}}\nolimits_2 \left[ {\frac{1}{8}\mathop {\sum}\limits_{x,y} {\mathrm{max}}_b(p(b|x,y))} \right].} \end{array}$$
(7)

To analyze the global randomness generation efficiency Hmin1, the maximal guessing probability \(\frac{1}{{16}}\mathop {\sum}\limits_{x,y,z} {\mathrm{max}}_{b,c}(p(b,c|x,y,z))\) can be estimated by

$$\begin{array}{l}\frac{1}{{16}}\mathop {\sum}\limits_{x,y,z} {\mathrm{max}}_{b,c}p(b,c|x,y,z)\\ = \frac{1}{{16}}\mathop {\sum}\limits_{x,y,z} {\mathrm{max}}_{b,c}p(b|x,y,z)p(c|x,y,z,b)\\ = \frac{1}{{16}}\mathop {\sum}\limits_{x,y,z} {\mathrm{max}}_{b,c}(p(b|x,y,z)p(c|x,z))\\ \le \left[ {\frac{1}{8}\mathop {\sum}\limits_{x,z} {\mathrm{max}}_cp(c|x,z)} \right] \times {\mathrm{max}}_{b,x,y,z}\left( {p\left( {b|x,y,z} \right)} \right.,\end{array}$$
(8)

where the second line is based on the condition for which Charlie’s measurement outcome c can not be effected by Bob, and the corresponding randomness generation efficiency Hmin1 is given by

$$H_{{\mathrm{min1}}} \ge - \mathop {{{\mathrm{log}}}}\nolimits_2 \left[ {\frac{1}{8}\mathop {\sum}\limits_{x,z} {\mathrm{max}}_c\left. {p(c|x,z)} \right)} \right] - \mathop {{{\mathrm{log}}}}\nolimits_2 [{\mathrm{max}}_{b,x,y,z}\left( {p(b|x,y,z)} \right.],$$
(9)

where the first part is the randomness generation in Charlie’s side, and the second part is the randomness generation in Bob’s side.

In the two-observer system, with a given random access code based dimension witness value W1, the relationship between W1 and the randomness generation efficiency \(H_{{\mathrm{min2}}}^{\prime} (W_1)\)26 is given by

$$H_{{\mathrm{min2}}}^{\prime} (W_1) = - \mathop {{{\mathrm{log}}}}\nolimits_2 \left( {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{1 + \sqrt {1 - (\frac{{W_1^2 - 4}}{4})^2} }}{2}} } \right).$$
(10)

However, the eavesdropper can apply Charlie’s input parameter z to guess Bob’s measurement outcome b, thus the previous method can not be directly applied in our protocol. To estimate the local randomness generation in Bob’s side, we will estimate the dimension witness value between Alice and Bob W1AB(z) with different input random number z ∈ {0,1} as follows

$$W_{1{\mathrm{AB}}(z = 0)} = W_{1{\mathrm{AB}}(z = 1)} = \sqrt 2 {\mathrm{cos}}(\epsilon ) + \sqrt 2 ,$$
(11)

with the detailed calculation is given in the Method section, and the corresponding local randomness generation efficiency in Bob’s side is \(H_{{\mathrm{min2}}}^{\prime} (W_1 = \sqrt 2{\mathrm{cos}}(\epsilon ) + \sqrt 2 )\).

With the given determinate value based on dimension witness W2 in the two-observer system, the relationship between the quantum dimension witness value W2 and the randomness generation efficiency \(H_{{\mathrm{min2}}}^{\prime \prime }\left( {W_2} \right)\)13 is given by

$$H_{{\mathrm{min2}}}^{\prime \prime }(W_2) = - \mathop {{{\mathrm{log}}}}\nolimits_2 \left( {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{{1 + \sqrt {1 - W_2^2} }}{2}} } \right).$$
(12)

Similar to the previous calculation, the dimension witness value between Alice and Bob W2AB(z) with different input random number z can be given by

$$W_{2{\mathrm{AB}}(z = 0)} = W_{2{\mathrm{AB}}(z = 1)} = {\mathrm{cos}}(\epsilon ),$$
(13)

with the detailed calculation is given in the Method section, and the corresponding local randomness generation efficiency in Bob’s side is \(H_{{\mathrm{min2}}}^{\prime \prime }(W_2 = {\mathrm{cos}}(\epsilon ))\).

Based on the previous analysis result, the detailed local randomness generation efficiency with different weak measurement parameter ε values are given in Fig. 3. Note that the local random number generation in Charlie’s side can be directly estimated by the two-observer protocol. Thus double local randomness generation can be realized if we choose an appropriate weak measurement parameter.

Fig. 3
figure 3

Local random number generation efficiency with different weak measurement parameters ε. The dashed green line corresponds to \(H_{{\mathrm{min2}}}^\prime (W_1 = \sqrt 2\, {\mathrm{cos}}(\epsilon ) + \sqrt 2 )\), and solid blue line corresponds to \(H_{{\mathrm{min}}2}^{\prime \prime }(W_2 = {\mathrm{cos}}(\epsilon ))\).

Full size image

Comparing with the random access code based protocol, the determinant value based protocol can provide the double classical dimension witness violation except the special case (ε = kπ, k = 0, 1, 2,...), thus it has the advantage in the experimental realization. However, the disadvantage is that this protocol has a strong assumption that the state preparation and measurement devices are independent.

Discussion

We proposed a three-observer dimension witness protocol, where the weak measurement technology was applied to analyze the double classical dimension witness violations. The results of our analysis shed new light on understanding the quantum dimension witness in the network environment. The three-observer dimension witness protocol can be assumed to be a sequential measurement protocol, and it will be interesting to analyze a higher dimensional multi-observer quantum system with sequential measurement27 technology. We demonstrated the randomness generation in the three-observer protocol, and the analysis results demonstrate that weak measurement may have significant applications in multi-observer semi-device-independent quantum information theory. This study also provides tremendous motivation for further experimental research.

Methods

Weak measurement protocol

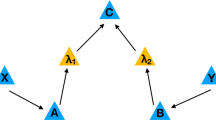
Weak measurement is a powerful method to extract less information about a system with smaller disturbance28, which has proven to be useful for signal amplification, state tomography, solving quantum paradoxes and others29,30,31,32,33. In this work, we use the weak measurement definition given in refs. 22,23,24, and the corresponding analysis model is given in Fig. 4.

Fig. 4
figure 4

Analysis model of three-observer classical dimension witness violation. Alice prepares the two-dimensional quantum state ρ x , and Bob and Charlie apply the two-dimensional strong measurement and weak measurement respectively

Full size image

There are three observers Alice, Bob and Charlie in the analysis model, and the purpose of our protocol is to establish double classical dimension witness violations under the two-dimensional Hilbert space restriction. More precisely, Alice prepares the two-dimensional quantum state ρ x  ∈ C2 and sends it through the quantum channel with a different classical input random number x ∈ {00,01,10,11}. Then, Charlie receives the quantum state and applies the following operation with the input random number z ∈ {0,1}

$$R_z^ + |0\rangle = |\omega _z\rangle , R_z^ + |1\rangle = |\omega _z^ \bot \rangle ,$$
(14)

where the above operation illustrates that the rotation maps the initial Hilbert space basis of {|0〉,|1〉} to a new basis of \(\{ |\omega _z\rangle ,|\omega _z^ \bot \rangle \}\) depending on the given z value. Charlie also has an two-dimensional ancillary quantum state \(| + \rangle = \frac{1}{{\sqrt 2 }}(|0\rangle + |1\rangle )\) in the quantum channel, and then, the following control operation is applied when Charlie receives the quantum state |1〉

$$e^{i\varepsilon \sigma _z} = \left( {\begin{array}{*{20}{c}} {e^{i\varepsilon }} & 0 & {} \\ 0 & {e^{ - i\varepsilon }} & {} \end{array}} \right).$$
(15)

where ε is the weak measurement parameter. If Charlie receives the quantum state |0〉, he will apply the identity operation \(I = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & 1 \end{array}} \right)\), thus the total unitary operation in Charlie’s side can be given by

$$\begin{array}{ccccc}\\ U = R_z^ + |0\rangle \langle 0|R_z \otimes I + R_z^ + |1\rangle \langle 1|R_z \otimes e^{i\varepsilon \sigma _z}\\ \\ = |\omega _z\rangle \langle \omega _z| \otimes I + |\omega _z^ \bot \rangle \langle \omega _z^ \bot | \otimes e^{i\varepsilon \sigma _z}\\ \\ = W_{\mathrm{B}}^{ + z} \otimes I + W_{\mathrm{B}}^{ - z} \otimes e^{i\varepsilon \sigma _z},\\ \end{array}$$
(16)

where we define \(W_{\mathrm{B}}^{ + z} = |\omega _z\rangle \langle \omega _z|\), \(W_{\mathrm{B}}^{ - z} = |\omega _z^ \bot \rangle \langle \omega _z^ \bot |\). Note that Charlie will apply the identity operation I if the weak measurement parameter ε is 0, which can be simply proved since \(W_{\mathrm{B}}^{ + z} \otimes I + W_{\mathrm{B}}^{ - z} \otimes I = I\). In this case, Charlie will only obtain the initial ancillary quantum state \(\left| + \right\rangle\) after the control operation, which demonstrates that Charlie can not gain any information about Alice’s state ρ x , and there is no interaction introduced by Charlie correspondingly.

To prove the dimension witness in the three-observer system, we should analyze the density matrix to illustrate Bob and Charlie’s system. The initial quantum state can be given by

$$\rho _{{\mathrm{BC}}x} = \rho _x \otimes | + \rangle \langle + |.$$
(17)

By applying the previous unitary transformation U, the quantum state ρBCx will be transformed into

$$\begin{array}{ccccc}\\ \rho _{{\mathrm{BC}}x}^\prime = U\rho _{{\mathrm{BC}}x}U^\dagger \hfill \\ \\ = W_{\mathrm{B}}^{ + z} \otimes I\rho _{{\mathrm{BC}}x}W_{\mathrm{B}}^{ + z} \otimes I \hfill\\ \\ \quad+ W_{\mathrm{B}}^{ + z} \otimes I\rho _{{\mathrm{BC}}x}W_{\mathrm{B}}^{ - z} \otimes e^{ - i\varepsilon \sigma _z}\hfill\\ \\ \quad + W_{\mathrm{B}}^{ - z} \otimes e^{i\varepsilon \sigma _z}\rho _{{\mathrm{BC}}x}W_{\mathrm{B}}^{ + z} \otimes I \hfill\\ \\ \quad+ W_{\mathrm{B}}^{ - z} \otimes e^{i\varepsilon \sigma _z}\rho _{{\mathrm{BC}}x}W_{\mathrm{B}}^{ - z} \otimes e^{ - i\varepsilon \sigma _z}.\\ \end{array}$$
(18)

The quantum state \({\rho}_{{\mathrm{Bx}}}^{\prime} = {\mathrm{Tr}}_{\mathrm{C}}{\rho}_{{\mathrm{BC}}x}^{\prime}\) will be transmitted to Bob, as follows

$$\begin{array}{ccccc}\\ \rho _{{\mathrm{B}}x}^\prime = {\mathrm{Tr}}_{\mathrm{C}}\rho _{{\mathrm{BC}}x}^\prime \\ \\ \quad\quad\quad\quad\quad\quad\quad\quad= W_{\mathrm{B}}^{ + z}\rho _xW_{\mathrm{B}}^{ + z} + W_{\mathrm{B}}^{ - z}\rho _xW_{\mathrm{B}}^{ - z}\\ \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad + \,{\mathrm{cos}}\,\epsilon (W_{\mathrm{B}}^{ + z}\rho _xW_{\mathrm{B}}^{ - z} + W_{\mathrm{B}}^{ - z}\rho _xW_{\mathrm{B}}^{ + z})\\ \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad= (1 - {\mathrm{cos}}(\epsilon ))(W_{\mathrm{B}}^{ + z}\rho _xW_{\mathrm{B}}^{ + z} + W_{\mathrm{B}}^{ - z}\rho _xW_{\mathrm{B}}^{ - z})\\ \\ + {\mathrm{cos}}(\epsilon )\rho _x.\\ \end{array}$$
(19)

Similarly, the quantum state \({\rho}_{{\mathrm{C}}x}^{\prime} = {\mathrm{Tr}}_{\mathrm{B}}{\rho}_{{\mathrm{BC}}x}^{\prime}\) will be transmitted to Charlie, as follows

$$\begin{array}{ccccc}\\ {\rho}_{{\mathrm{C}}x}^{\prime} = {\mathrm{Tr}}_{\mathrm{B}}{\rho}_{{\mathrm{BC}}x}^{\prime} \\ \\ \quad\quad\quad\quad\quad\quad= {\mathrm{Tr}}_{\mathrm{B}}(W_{\mathrm{B}}^{ + z}{\rho}_x)\left| + \right\rangle \langle + |\\ \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad+ {\mathrm{Tr}}_{\mathrm{B}}(W_{\mathrm{B}}^{ - z}{\rho}_x)e^{i\varepsilon \sigma _z}| + \rangle \langle + |e^{ - i\varepsilon \sigma _z}.\\ \end{array}$$
(20)

After receiving the quantum state \({\rho}_{Bx}^{\prime}\), Bob will apply the two-dimensional projective measurement depending on the input random number y ∈ {0,1}. If Bob’s input random number is 0, the corresponding measurement basis in Bob’s side is given by

$$\{ |\nu _0\rangle \langle \nu _0|,|\nu _0^ \bot \rangle \langle \nu _0^ \bot |\} .$$
(21)

If Bob’s input is 1, Bob’s measurement basis is

$$\{ |\nu _1\rangle \langle \nu _1|,|\nu _1^ \bot \rangle \langle \nu _1^ \bot |\} ,$$
(22)

where the measurement outcomes |ν0〉〈ν0| and |ν1〉〈ν1| indicate classical bit 1, and the measurement outcomes \(|\nu _0^ \bot \rangle \langle \nu _0^ \bot |\) and \(|\nu _1^ \bot \rangle \langle \nu _1^ \bot |\) indicate classical bit −1.

After receiving the quantum state \({\rho}_{Cx}^{\prime}\), Charlie will apply the two-dimensional projective measurement

$$\{ |t\rangle \langle t|,|t^ \bot \rangle \langle t^ \bot |\} ,$$
(23)

where the measurement outcomes |t〉〈t| and |t⊥〉〈t⊥| respectively indicate the classical bit 1 and −1. Before the state measurement, Charlie randomly chooses rotation \(\{ R_z,R_z^ + \}\) with respect to the input random number z ∈ {0,1}.

In the case where the weak measurement parameter ε is 0, there is no interaction on Charlie’s side, and then, Charlie’s density matrix will be transformed into \({\rho}_{{\mathrm{C}}x}^{\prime} = {\mathrm{Tr}}_{\mathrm{B}}(W_{\mathrm{B}}^{ + z}{\rho}_x + W_{\mathrm{B}}^{ - z}{\rho}_x)| + \rangle \langle + | = | + \rangle \langle + |\), and Bob’s density matrix will be transformed into \({\rho}_{{\mathrm{B}}x}^{\prime} = {\rho}_x\). In the following section, we will focus on the situation 0 ≤ ε ≤ π, and analyze the interaction introduced by the weak measurement, which can be used to obtain the information gain in Charlie’s side.

The general representation of a qubit can be illustrated by using the density matrix formalism \(\frac{{I + \vec r \cdot \vec \sigma }}{2}\), where \(\vec \sigma\) is the Pauli matrix vector \(\left( {\sigma _x = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ 1 & 0 \end{array}} \right),\sigma _y = \left( {\begin{array}{*{20}{c}} 0 & { - i} \\ i & 0 \end{array}} \right),\sigma _z = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & { - 1} \end{array}} \right)} \right)\), and \(\vec r = (r_x,r_y,r_z)\) is a real three-dimensional vector such that \(\left\| r \right\| \le 1\), thus the conditional probability distribution to illustrate Alice and Bob’s system can be given by

$$\begin{array}{ccccc}\\ p(b|xy) = \mathop {\sum}\limits_z p(z){\mathrm{Tr}}({\mathrm{B}}_y^b\rho _{{\mathrm{B}}x}^\prime (z))\hfill\\ \\ = \frac{1}{2}(1 - {\mathrm{cos}}(\epsilon ))\mathop {\sum}\limits_z p(z)b\omega _z \cdot \nu _y \times \omega _z \cdot \rho _x\\ \\ \quad+ \frac{1}{2}{\mathrm{cos}}(\epsilon )(1 + b\nu _y \cdot \rho _x) + \frac{1}{2}(1 - {\mathrm{cos}}(\epsilon )),\\ \end{array}$$
(24)

where \({\mathrm{B}}_y^b\) is the measurement operator acting on the two-dimensional Hilbert space with input parameter y and output parameter b by considering the prepared quantum state \({\rho}_{{\mathrm{B}}x}^{\prime} (z)\). The conditional probability distribution to illustrate Alice and Charlie’s system is given by

$$\begin{array}{ccccc}\\ p({\mathrm{c}}|xz) = {\mathrm{Tr}}(C^c\rho _{Cx}^\prime (z))\\ \\ \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad= \frac{1}{2}(1 + \omega _z \cdot \rho _x)(1 + {\mathrm{c}} - {\mathrm{c}}\,\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon )),\\ \end{array}$$
(25)

where Cc is the measurement operator acting on the two-dimensional Hilbert space to obtain the measurement outcome c with the state \(\rho_{{\mathrm{C}}x}^{\prime} (z)\).

Based on the previous observed statistics p(b|xy) and p(c|xz), we can calculate the dimension witness value between Alice and Bob and between Alice and Charlie respectively.

Three-observer dimension witness based on quantum random access code

The general representation of a qubit can be illustrated by using the density matrix formalism \(\frac{{I + \vec r \cdot \vec \sigma }}{2}\), where \(\vec \sigma\) is the Pauli matrix vector \(\left( {\sigma _x = \left( {\begin{array}{*{20}{c}} 0 & 1 \\ 1 & 0 \end{array}} \right),\sigma _y = \left( {\begin{array}{*{20}{c}} 0 & { - i} \\ i & 0 \end{array}} \right),\sigma _z = \left( {\begin{array}{*{20}{c}} 1 & 0 \\ 0 & { - 1} \end{array}} \right)} \right)\), and \(\vec r = (r_x,r_y,r_z)\) is a real three-dimensional vector such that \(\left\| r \right\| \le 1\). In the following section, we apply \(\vec r = (r_x,r_y,r_z)\) to demonstrate the quantum state ρ x (x ∈ {00,01,10,11}), |ν y 〉〈ν y | (y ∈ {0,1}), |ω z 〉〈ω z | (z ∈ {0,1}) and |t〉〈t|.

To prove the double classical dimension witness violation under Eq. (1), we propose the following density matrix prepared in Alice’s side

$$\begin{array}{l}{\rho}_{00} = \left( {\frac{1}{{\sqrt 2 }},0,\frac{1}{{\sqrt 2 }}} \right),\\ {\rho}_{01} = \left( { - \frac{1}{{\sqrt 2 }},0,\frac{1}{{\sqrt 2 }}} \right),\\ {\rho}_{10} = \left( {\frac{1}{{\sqrt 2 }},0, - \frac{1}{{\sqrt 2 }}} \right),\\ {\rho}_{11} = \left( { - \frac{1}{{\sqrt 2 }},0, - \frac{1}{{\sqrt 2 }}} \right).\end{array}$$
(26)

The measurement operator in Bob’s side is given by

$$\begin{array}{l}\nu _0 = (0,0,1),\\ \nu _1 = (1,0,0).\end{array}$$
(27)

The measurement operator in Charlie’s side is given by

$$t = (1,0,0).$$
(28)

The rotation operator in Charlie’s side is given by

$$\begin{array}{l}\omega _0 = (0,0,1),\\ \omega _1 = (1,0,0).\end{array}$$
(29)

Based on the previous state preparation and measurement operator, we can calculate the corresponding conditional probability distribution p(b = 1|x,y) AB with different classical input random numbers x ∈ {00,01,10,11} and y ∈ {0,1}.

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}}} = \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 + \sqrt 2 }}{8},\\ p(1|001)_{{\mathrm{AB}}} = \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 + \sqrt 2 }}{8},\\ p(1|010)_{{\mathrm{AB}}} = \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 + \sqrt 2 }}{8},\\ p(1|011)_{{\mathrm{AB}}} = - \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 - \sqrt 2 }}{8},\\ p(1|100)_{{\mathrm{AB}}} = - \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 - \sqrt 2 }}{8},\\ p(1|101)_{{\mathrm{AB}}} = \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 + \sqrt 2 }}{8},\\ p(1|110)_{{\mathrm{AB}}} = - \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 - \sqrt 2 }}{8},\\ p(1|111)_{{\mathrm{AB}}} = - \frac{{\sqrt 2 }}{8}{\mathrm{cos}}(\epsilon ) + \frac{{4 - \sqrt 2 }}{8}.\end{array}$$
(30)

By applying the previous conditional probability distributions p(b = 1|x,y) AB , the dimension witness value10, 11, 18 between Alice and Bob is given by

$$\begin{array}{ccccc}\\ W_{1{\mathrm{AB}}} = p(1|000)_{{\mathrm{AB}}} + p(1|001)_{{\mathrm{AB}}} + p(1|010)_{{\mathrm{AB}}}\\ \\ - p(1|011)_{{\mathrm{AB}}} - p(1|100)_{{\mathrm{AB}}} + p(1|101)_{{\mathrm{AB}}}\\ \\ - p(1|110)_{{\mathrm{AB}}} - p(1|111)_{{\mathrm{AB}}}\\ \\ = \sqrt 2 ({\mathrm{cos}}(\varepsilon ) + 1).\\ \end{array}$$
(31)

Based on the previous state preparation and measurement operator, we can calculate the corresponding conditional probability distribution p(b = 1|x,z)AC as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AC}}} = \frac{{2 + \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|001)_{{\mathrm{AC}}} = \frac{{2 + \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|010)_{{\mathrm{AC}}} = \frac{{2 + \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|011)_{{\mathrm{AC}}} = \frac{{2 - \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|100)_{{\mathrm{AC}}} = \frac{{2 - \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|101)_{{\mathrm{AC}}} = \frac{{2 + \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|110)_{{\mathrm{AC}}} = \frac{{2 - \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|111)_{{\mathrm{AC}}} = \frac{{2 - \sqrt 2 }}{4}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ).\end{array}$$
(32)

By applying the previous conditional probability distributions p(b = 1|x,y)AC, the dimension witness value between Alice and Charlie is given by

$$W_{1{\mathrm{AC}}} = 2\sqrt 2 \mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ).$$
(33)

To prove local randomness generation in Bob’s side, we analyze the dimension witness value W1ABz with different input weak measurement parameters z ∈ {0,1}.

In the case of z = 0, we can obtain the corresponding conditional probability distributions p(b = 1|x,y)AB,z = 0 as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}},\,z = 0} = \frac{{2 + \sqrt 2 }}{4},\\ p(1|001)_{{\mathrm{AB}},\, z = 0} = \frac{{2 + \sqrt 2 {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|010)_{{\mathrm{AB}},\,z = 0} = \frac{{2 + \sqrt 2 }}{4},\\ p(1|011)_{{\mathrm{AB}},\,z = 0} = \frac{{2 - \sqrt 2 {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|100)_{{\mathrm{AB}},\,z = 0} = \frac{{2 - \sqrt 2 }}{4},\\ p(1|101)_{{\mathrm{AB}},\,z = 0} = \frac{{2 + \sqrt 2 {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|110)_{{\mathrm{AB}},\,z = 0} = \frac{{2 - \sqrt 2 }}{4},\\ p(1|111)_{{\mathrm{AB}},\,z = 0} = \frac{{2 - \sqrt 2\, {\mathrm{cos}}(\epsilon )}}{4}.\end{array}$$
(34)

By applying the previous conditional probability distributions p(b = 1|x,y)AB,z = 0, the dimension witness value between Alice and Bob is given by

$$W_{1{\mathrm{AB}},\,z = 0} = \sqrt 2\, {\mathrm{cos}}(\epsilon ) + \sqrt 2 .$$
(35)

In the case of z = 1, we obtain the corresponding conditional probability distribution p(b = 1|x,y)AB,z = 1 as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}},\,z = 1} = \frac{{2 + \sqrt 2\, {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|001)_{{\mathrm{AB}},\,z = 1} = \frac{{2 + \sqrt 2 }}{4},\\ p(1|010)_{{\mathrm{AB}},\,z = 1} = \frac{{2 + \sqrt 2 {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|011)_{{\mathrm{AB}},\,z = 1} = \frac{{2 - \sqrt 2 }}{4},\\ p(1|100)_{{\mathrm{AB}},\,z = 1} = \frac{{2\, - \sqrt 2 {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|101)_{{\mathrm{AB}},\,z = 1} = \frac{{2 + \sqrt 2 }}{4},\\ p(1|110)_{{\mathrm{AB}},\,z = 1} = \frac{{2 - \sqrt 2\, {\mathrm{cos}}(\epsilon )}}{4},\\ p(1|111)_{{\mathrm{AB}},\,z = 1} = \frac{{2 - \sqrt 2 }}{4}.\end{array}$$
(36)

By applying the previous conditional probability distributions p(b = 1|x,y)AB,z = 1, the dimension witness value between Alice and Bob is given by

$$W_{1{\mathrm{AB}},\,z = 1} = \sqrt 2 {\mathrm{cos}}(\epsilon ) + \sqrt 2 .$$
(37)

Three-observer dimension witness based on determinant value

To prove the double classical dimension witness violation under Eq. (4), we propose the following density matrix preparation in Alice’s side

$$\begin{array}{l}{\rho}_{00} = (0,0,1),\\ {\rho}_{01} = (0,0, - 1),\\ {\rho}_{10} = (1,0,0),\\ {\rho}_{11} = ( - 1,0,0).\end{array}$$
(38)

The measurement operator in Bob’s side is given by

$$\begin{array}{l}\nu _0 = (0,0,1),\\ \nu _1 = (1,0,0).\end{array}$$
(39)

The measurement operator in Charlie’s side is given by

$$t = (1,0,0).$$
(40)

The rotation operator in Charlie’s side is given by

$$\begin{array}{l}\omega _0 = (0,0,1),\\ \omega _1 = (1,0,0).\end{array}$$
(41)

Note that the state preparation and measurement operator are the same as the Bennett and Brassard 1984 (BB84) quantum key distribution protocol34, but the weak measurement model may disturb Alice’s quantum state with the different weak measurement parameter ε, and this disturbance can be detected by the quantum bit error rate.

Based on the previous state preparation and measurement, we can calculate the corresponding conditional probability distribution p(b = 1|x,y) AB as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}}} = \frac{1}{4}{\mathrm{cos}}(\epsilon ) + \frac{3}{4},\\ p(1|001)_{{\mathrm{AB}}} = \frac{1}{2},\\ p(1|010)_{{\mathrm{AB}}} = - \frac{1}{4}{\mathrm{cos}}(\epsilon ) + \frac{1}{4},\\ p(1|011)_{{\mathrm{AB}}} = \frac{1}{2},\\ p(1|100)_{{\mathrm{AB}}} = \frac{1}{2},\\ p(1|101)_{{\mathrm{AB}}} = \frac{1}{4}{\mathrm{cos}}(\epsilon ) + \frac{3}{4},\\ p(1|110)_{{\mathrm{AB}}} = \frac{1}{2},\\ p(1|111)_{{\mathrm{AB}}} = - \frac{1}{4}{\mathrm{cos}}(\epsilon ) + \frac{1}{4}.\end{array}$$
(42)

By applying the previous conditional probability distributions p(b = 1|x,y) AB , the dimension witness value13, 14 between Alice and Bob is given by

$$\begin{array}{l}W_{2{\mathrm{AB}}}\\ = \left| {\begin{array}{*{20}{c}} {p(1|000)_{{\mathrm{AB}}} - p(1|010)_{{\mathrm{AB}}}} & {p(1|100)_{{\mathrm{AB}}} - p(1|110)_{{\mathrm{AB}}}} \\ {p(1|001)_{{\mathrm{AB}}} - p(1|011)_{{\mathrm{AB}}}} & {p(1|101)_{{\mathrm{AB}}} - p(1|111)_{{\mathrm{AB}}}} \end{array}} \right|\\ = \left( {\frac{1}{2}{\mathrm{cos}}(\varepsilon ) + \frac{1}{2}} \right)^2.\end{array}$$
(43)

Based on the previous state preparation and measurement, we can also calculate the corresponding conditional probability distribution p(b = 1|x,z)AC as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AC}}} = \mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|001)_{{\mathrm{AC}}} = \frac{1}{2}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|010)_{{\mathrm{AC}}} = 0,\\ p(1|011)_{{\mathrm{AC}}} = \frac{1}{2}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|100)_{{\mathrm{AC}}} = \frac{1}{2}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|101)_{{\mathrm{AC}}} = \mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|110)_{{\mathrm{AC}}} = \frac{1}{2}\mathop {{{\mathrm{sin}}}}\nolimits^2 (\epsilon ),\\ p(1|111)_{{\mathrm{AC}}} = 0.\end{array}$$
(44)

By applying the previous conditional probability distributions p(b = 1|x,y)AC, the dimension witness value between Alice and Charlie is given by

$$W_{2{\mathrm{AC}}} = \mathop {{{\mathrm{sin}}}}\nolimits^4 (\epsilon ).$$
(45)

To prove local randomness generation in Bob’s side, we will analyze the dimension witness value W2ABz with different input weak measurement parameters z ∈ {0,1}.

In the case of z = 0, we can obtain the corresponding conditional probability distribution p(b = 1|x,y)AB,z = 0 as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}},z = 0} = 1,\\ p(1|001)_{{\mathrm{AB}},z = 0} = \frac{1}{2},\\ p(1|010)_{{\mathrm{AB}},z = 0} = 0,\\ p(1|011)_{{\mathrm{AB}},z = 0} = \frac{1}{2},\\ p(1|100)_{{\mathrm{AB}},z = 0} = \frac{1}{2},\\ p(1|101)_{{\mathrm{AB}},z = 0} = \frac{{1 + {\mathrm{cos}}(\epsilon )}}{2},\\ p(1|110)_{{\mathrm{AB}},z = 0} = \frac{1}{2},\\ p(1|111)_{{\mathrm{AB}},z = 0} = \frac{{1 - {\mathrm{cos}}(\epsilon )}}{2}.\end{array}$$
(46)

Based on the previous conditional probability distributions p(b = 1|x,y)AB,z = 0, the dimension witness value between Alice and Bob is given by

$$W_{2{\mathrm{AB}},z = 0} = {\mathrm{cos}}(\epsilon ).$$
(47)

In the case of z = 1, we can obtain the corresponding conditional probability distribution p(b = 1|x,y)AB,z = 1 as follows

$$\begin{array}{l}p(1|000)_{{\mathrm{AB}},z = 1} = \frac{{1 + {\mathrm{cos}}(\epsilon )}}{2},\\ p(1|001)_{{\mathrm{AB}},z = 1} = \frac{1}{2},\\ p(1|010)_{{\mathrm{AB}},z = 1} = \frac{{1 - {\mathrm{cos}}(\epsilon )}}{2},\\ p(1|011)_{{\mathrm{AB}},z = 1} = \frac{1}{2},\\ p(1|100)_{{\mathrm{AB}},z = 1} = \frac{1}{2},\\ p(1|101)_{{\mathrm{AB}},z = 1} = 1,\\ p(1|110)_{{\mathrm{AB}},z = 1} = \frac{1}{2},\\ p(1|111)_{{\mathrm{AB}},z = 1} = 0.\end{array}$$
(48)

By applying the previous conditional probability distributions p(b = 1|x,y)AB,z = 1, the dimension witness value between Alice and Bob is given by

$$W_{2{\mathrm{AB}},z = 1} = {\mathrm{cos}}(\epsilon ).$$
(49)

Code availability

Source codes of the plots are available from the corresponding authors on request.

Data availability

The data that support the findings of this study are available from the corresponding authors on request.