Abstract
Black phosphorus is considered a very promising semiconductor for two-dimensional field-effect transistors. Initially, the main disadvantage of this material was thought to be its poor air stability. However, recent studies have shown that this problem can be solved by suitable encapsulation. As such, long-term studies of the outstanding properties of black phosphorus devices have become possible. In particular, here we examine highly-stable black phosphorus field-effect transistors and demonstrate that they can exhibit reproducible characteristics for at least 17 months. Furthermore, we notice some improvement in the performance of black phosphorus devices after this long time, i.e., positive aging. Although our black phosphorus devices are stable at room temperature, we show that their performance is affected by thermally activated charge trapping by oxide traps into the adjacent SiO2 substrate layer. Aiming to analyze the dynamics of these defects in detail, we perform an accurate mapping of oxide traps with different time constants using the ‘extended incremental hysteresis sweep method’. Our results show that at room temperature the extracted oxide trap densities are (i) few orders of magnitude lower than for MoS2/SiO2 transistors and (ii) close to those reported for more mature Si/SiO2 devices (~1017 cm−3 eV−1). Taking into account the novelty of black phosphorus and recent issues with its stability, these values must be considered unexpectedly low.
Similar content being viewed by others
Introduction
Black phosphorus (BP) is a crystalline two-dimensional (2D) semiconductor which is now considered for applications in next-generation optoelectronic devices.1,2,3 With its direct optical bandgap ranging from 0.3 eV in bulk to over 1 eV in the single-layer limit,1, 4 BP is able to outperform graphene5 in digital device applications. At the same time, the comparatively high hole mobility up to 1000 cm2/Vs makes BP a promising candidate as a channel material in p-FETs,3 which would nicely complement MoS2 n-FETs6,7,8,9 in integrated or flexible CMOS circuits. Furthermore, the electron mobility in BP is also larger than in MoS2, which makes it interesting for n-FETs as well.10 In addition, the recently demonstrated epitaxial synthesis of monolayer phosphorene represents a breakthrough for very large scale integration.11
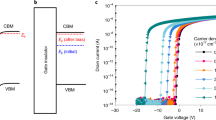
Several successful attempts at fabricating black phosphorus field-effect transistors (BPFETs) have been reported recently.1, 12,13,14 However, so far the poor air stability of these devices only allowed analysis of their basic characteristics such as on/off current ratios and mobilities. At the same time, the analysis of the long-term stability and reliability of BPFETs, which has to be understood for any material system that is to acquire some technological significance, has only become possible now due to the recent introduction of conformal capping schemes (Fig. 1a).13, 15
a While the uncovered device is unstable in air, the conformally encapsulated sample studied here guarantees long-term stability. b Schematic layout of our BPFETs with Al2O3 encapsulation. c Measurement activity vs. time since fabrication of our devices. “0” means that the devices have been stored in ambient conditions, while “1” expresses intensive measurements in vacuum (mostly electrical stressing, 0.5–2.5 MV/cm) at various temperatures (27 to 165 °C). The gate transfer (I d − V g) characteristics measured for the same device at different stages of our long-term study. d The gate transfer characteristics of our BPFET measured at different temperatures. e The hysteresis widths ΔV Hn and ΔV Hp follow an Arrhenius dependence
The stability and reliability of all 2D transistors investigated so far is reduced by charge trapping in oxide traps16,17,18 with very broad distributions of time constants.19 This presents one of the main road blocks towards commercialization of 2D technologies. In its most obvious form, charge trapping results in a hysteresis, which is typically observed on the gate transfer characteristics.9, 20,21,22 The magnitude of this hysteresis depends on the density of active oxide traps D ot, which can contribute to charge trapping, thus leading to variations of the device threshold voltage. As such, in order to minimize the hysteresis and improve the device stability and reliability, D ot must be minimized. Furthermore, the oxide traps in every insulator are located within certain defect bands23 with the maximum oxide trap density in the middle.24 In particular, the number of oxide traps which are accessible for charge trapping depends on the energetic alignment of these defect bands relative to the conduction and valence band of the channel. Therefore, the determination of both density and energetic alignment of these defect bands is of utmost importance, especially for such unexplored system as BP/SiO2. Here we extend our incremental hysteresis sweep method which has been previously developed for MoS2 FETs25 to the case of BPFETs and determine the energy distributions of oxide traps in these devices. While demonstrating that our BPFETs remain highly stable for at least 17 months, we show that at room temperature the oxide trap density can be as low as 1017 cm−3 eV−1, which is already close to values obtained for commercial Si devices.
Results and discussion
We examine few-layer BPFETs with 80-nm thick SiO2 as a gate insulator and L = 500 nm (Fig. 1b). BP flakes were mechanically exfoliated directly onto the Si/SiO2 substrate and selected according to optical contrast to have a thickness of less than 15 nm (see Fig. S1 in the Supporting Information (SI)). In order to prevent severe degradation of the BP film in ambient air,13, 15, 26 our BPFETs have been conformally encapsulated with a 25 nm thick Al2O3 layer. The total time since fabrication of our BPFETs till the end of this study is around 17 months, during which we have either performed intensive measurements (mostly stressing of the device in vacuum) or stored the devices in ambient conditions. In Fig. 1c, we show the gate transfer (I d − V g) characteristics measured at different stages of our long-term study. Remarkably, some drifts are observed only after several months of intensive measurements, while long storage in ambient conditions does not have any significant impact on the device performance. Furthermore, the consecutively measured I d − V g characteristics in a vacuum and in ambient conditions are similar, which further confirms the high stability of our devices. Also, it is worth noting that the most recent I d − V g characteristics exhibit the smallest hysteresis and the highest on/off current ratio, possibly due to the annealing of process-induced defects or adsorbed species like water (for more details see Fig. S2 in the SI). Furthermore, the subthreshold slope becomes steeper after several months, meaning that our BPFETs improve over time, despite the heavy stresses they were exposed to. This improvement over time is known as positive aging and can originate from some microscopic changes in the BP channel, which would require a dedicated separate long-term study.
Although our BPFETs are very stable and exhibit only a negligible hysteresis at room temperature, unlike graphene27 and MoS2 22, 28 devices; in Fig. 1d we show that at higher temperatures the hysteresis becomes considerably stronger. As shown in Fig. 1e, the hysteresis widths extracted at a constant current in the electron (ΔV Hn) and hole (ΔV Hp) conduction regions follow an Arrhenius law with activation energy 260 meV. This suggests that the hysteresis in our BPFETs is due to thermally activated charge trapping in the oxide. As such, further improvement of the stability and performance of BPFETs requires a detailed study of oxide traps.
Although the ambient does not have any considerable impact on the characteristics of our BPFETs, our measurements were initially performed in a vacuum (5 × 10−6–10−5 torr), since the temperature has been varied up to 165 °C and we did not expect these devices to be so stable. Aiming to map the oxide traps with widely distributed time constants and different energy levels, we extend our experimental technique previously suggested for MoS2 FETs25 to the case of ambipolar BPFETs. Namely, in unipolar MoS2 devices we measured the hysteresis with a fixed V gmin and stepped V gmax, while using forward (V +) and reversed (V −) sweep directions and different sweep rates. In order to capture the impact of oxide traps on the device performance in both the electron and hole conduction regions, here we perform the measurements using both a fixed V gmin and stepped V gmax, as well as a fixed V gmax and stepped V gmin (for the details see Fig. S3 in the SI and also the Methods section). Then, similarly to ref. 29, we introduce the measurement frequency f = 1/(Nt step), with N being the number of voltage steps and t step the sampling time. This allows us to express the measurement results in terms of ΔV Hn(f) and ΔV Hp(f) for varied V gmax and V gmin, respectively. These dependences contain information about the spatial and energy distribution of the density of charged oxide traps with different time constants within the whole device operation range.
In Fig. 2 we monitor the transformation of the I d − V g characteristics measured at T = 165 °C using different sweep rates and sweep ranges with respect to the fast hysteresis-free reference curves obtained using S = 1000 V/s. If the sweep range −20 to 1 V is used (Fig. 2a), the charge neutrality point \(V_{{\rm{NP}}}^ + \) becomes more negative as S is decreased. As shown by the schematic band diagrams, this means that some of those defects which had been above the Fermi level E F while passing through the hole conduction region have captured a hole. This issue presents nothing else than the well-known negative bias-temperature instability (NBTI).30 At the same time, \(V_{{\rm{NP}}}^ - \) is more positive, which is due to the emission of holes by those defects which are below E F around V gmax, thus triggering a shift due to positive BTI (PBTI).30 As a result, a combination of the NBTI and PBTI contributions leads to a hysteresis in the I d − V g characteristics. Remarkably, ΔV Hn is very sensitive to variations of V gmax and becomes larger even if it is increased by only 1 V. Therefore, for the sweep range −20 to 20 V (Fig. 2b), the emission of a large number of holes while approaching V gmax leads to a large hysteresis. Finally, for the sweep range −1 to 20 V (Fig. 2c) the hysteresis is again small, since the number of those defects which can capture a hole around V gmin is negligible. Nevertheless, ΔV Hp is sensitive to V gmin and becomes larger even for a small shift of only −1 V. Note that the sensitivity of ΔV Hn to V gmax and ΔV Hp to V gmin contains the unique fingerprint of the density of charged oxide traps.
The I d − V g characteristics measured using different sweep ranges. a −20 to 1 V. For slow sweeps, many defects can capture a hole (i.e., become charged) within the hole conduction region. This makes \(V_{{\rm{NP}}}^ + \) more negative than it was for the reference curve (S = 1000 V/s). At the same time, a small V gmax limits hole emission in the electron conduction region, which leads to a small hysteresis. Furthermore, an increase of V gmax makes hole emission more effecient and leads to a more positive \(V_{{\rm{NP}}}^ - \) and larger ΔV Hn (inset). b −20 to 20 V. The total hysteresis width is mainly due to hole emission. c −1 to 20 V. The contribution of hole capture is negligible due to the small absolute V gmin. The hysteresis width ΔV Hp is sensitive to V gmin (inset)
Taking into account the results of Fig. 2, we can separate the NBTI and PBTI contributions by splitting the total hysteresis width into the threshold voltage shifts Δ\(V_{{\rm{Tn}}}^ + \) and Δ\(V_{{\rm{Tn}}}^ - \). These quantities are measured relative to the hysteresis-free fast sweep curve using the V + and V − sweep modes, respectively (for more details see Fig. S4 in the SI). Following this approach, in Fig. 3a we provide the Δ\(V_{{\rm{Tn}}}^ + \)(f) and Δ\(V_{{\rm{Tn}}}^ - \)(f) curves obtained at T = 95 °C, T = 130 °C and T = 165 °C using V gmin = −20 V and V gmax between 1 and 20 V. Clearly, at higher temperatures both Δ\(V_{{\rm{Tn}}}^ + \)(f) and Δ\(V_{{\rm{Tn}}}^ - \)(f) become larger, which is because of the thermal activation of charge capture and emission. While negligible variations of Δ\(V_{{\rm{Tn}}}^ + \)(f) for different V gmax originate from a slight drift of the device in between different loops, the Δ\(V_{{\rm{Tn}}}^ - \)(f) curves follow an increase of V gmax. As V gmax increases, the number of traps which are shifted below the Fermi level due to band-bending and thus can emit a hole, becomes larger. This leads to a larger PBTI contribution. As such, the concentration of oxide traps which come into play between \(V_{{\rm{gmax}}}^i\) and \(V_{{\rm{gmax}}}^{i + 1}\) is
Taking into account the tunnel charge exchange between oxide traps and the channel, we performed WKB calculations and found that only traps situated within d ≈ 3 nm from the BP/SiO2 interface can contribute to the charge trapping processes within our experimental window (1 ks). Therefore, we can calculate the average oxide trap density within the electron conduction region from the obtained set of Δ\(V_{{\rm{Tn}}}^ - \)(f) curves as
with C ox being the oxide capacitance and q the elementary charge.
a The Δ\(V_{{\rm{Tn}}}^ + \)(f) and Δ\(V_{{\rm{Tn}}}^ - \)(f) characteristics obtained at T = 95 °C, T = 130 °C and T = 165 °C for V gmin = −20 V and V gmax from 1 to 20 V. While for larger V gmax the number of defects which can emit a hole becomes larger, the distances between the Δ\(V_{{\rm{Tn}}}^ - \)(f) curves are proportional to the concentrations of oxide traps which discharge within the corresponding V g interval. b The Δ\(V_{{\rm{Tp}}}^ + \)(f) and Δ\(V_{{\rm{Tp}}}^ - \)(f) characteristics obtained for the same temperatures using V gmax = 20 V and different V gmin. Since V gmin determines the number of traps which can become charged, we analyze the distances between the Δ\(V_{{\rm{Tp}}}^ + \)(f) curves. However, since for narrow sweep ranges Δ\(V_{{\rm{Tp}}}^ + \) is not accessible, we have to use the Δ\(V_{{\rm{Tn}}}^ + \)(f) curves (inset)
The corresponding results for V gmax = 20 V and V gmin between 0 and −20 V are shown in Fig. 3b. In order to capture the impact of V gmin without considerable time delay, we analyze the Δ\(V_{{\rm{Tp}}}^ + \)(f) and Δ\(V_{{\rm{Tp}}}^ - \)(f) dependences, except for the case of narrow sweep ranges when the hole conduction region is not accessible. Since V gmin impacts the number of traps which can capture a hole and the magnitude of the NBTI contribution, the information about the defect distribution is contained in the Δ\(V_{{\rm{Tp|n}}}^ + \)(f) dependences. Therefore, for the hole conduction region
Processing of the experimental results given in Fig. 3 using the Eqs. (1)–(4) allow us to obtain the D ot(V g) distributions within the whole device operation range from −20 to 20 V. However, since we are here interested in the energy distributions of D ot, we next convert V g into the electronic energy E. In order to do this, we consider the band diagrams and the alignment of the defect bands in SiO2 obtained using technology computer-aided design (TCAD) simulations.30, 31 From conventional Si technologies24, 32 and our previous work on BP devices30 it is known that SiO2 contains two distinct defect bands, whereby the upper defect band is most likely of acceptor-type (i.e., in equilibrium the defects are negatively charged below and neutral above the Fermi level) and the lower defect band is of donor-type (i.e., the defects are neutral below and positively charged above the Fermi level). The performance of BPFETs is mainly affected by the defects of the upper defect band located at \(E_{\rm{T}}^u = 2.75 \pm 0.4\) eV below the SiO2 conduction band edge.30 Thus, by considering the band-bending around the trap level \(E_{\rm{T}}^{\rm{u}}\) within 3 nm from the interface, we evaluate the \(E_{\rm{T}}^{\rm{u}}\)(V g) dependence, while expressing \(E_{\rm{T}}^{\rm{u}}\) in the units of the electronic energy E referred from the middle of the Si bandgap, which is just 0.26 eV below the middle of the BP bandgap (a detailed discussion can be found in the SI, see Fig. S5). This brings us to the energy distributions of oxide traps D ot(E). Note that our TCAD setup is similar to the one used in our previous work,30 except that we had previously assumed the upper band to be of donor-type. However, this assumption does not affect the magnitude of the simulated hysteresis and only shifts the flat-band voltage by a constant amount. Therefore, taking into account that in ref. 30 we obtained reasonable TCAD fits of the measured BTI characteristics by disregarding the Al2O3 encapsulation and all possible non-SiO2 defects, we assume that the possible trapping states at the Al2O3/BP interface as well as residual impurities and BP defects do not have any considerable impact on our results and are thus negligible.
The D ot(E) distributions obtained for T = 95, 130 and 165 °C and the measurement frequency between 5 × 10−4 and 1 Hz are shown in Fig. 4a–c. We can clearly discern the regions with dominating hole capture and emission, which correspond to the measurements with varied V gmin and V gmax, respectively. Both processes become more effecient for smaller f, which means that traps with larger time constants are dominant. However, in most cases emission is more sensitive to f than capture, which indicates that the emission times are more widely distributed than the capture times. At the same time, at higher temperature the impact of f becomes more pronounced. As such, the time constants of all defects become smaller, which is fully consistent with thermally activated charge trapping. Interestingly, the various features observed in the shape of the D ot(E) curves are well reproduced at different temperatures (Fig. 4d) and also for different devices (see Fig. S6 in the SI). This confirms that the non-homogeneous density of charged oxide traps can be captured reasonably well using our extended incremental hysteresis sweep method. Finally, in Fig. 4e we compare the typical D ot extracted for our BPFETs with literature values for different technologies.33,34,35,36,37,38,39,40 At room temperature the density of active oxide traps in our devices is ~1017 cm−3 eV−1, which is close to Si/SiO2 FETs with D ot ~ 5 × 1016 cm−3 eV−1. At the same time, this is considerably lower than for MoS2/SiO2 and Si/high-k devices, in which D ot can exceed 1020 cm−3 eV−1. Although at T = 165 °C D ot increases, the obtained values (~1019 cm−3 eV−1) remain reasonable. The possible reasons for the comparably small D ot values in our BPFETs are the following: First, optimization of the device processing conditions allowed us to reduce the number of those process-induced defects which can contribute to charge trapping. At the same time, the use of an effective encapsulation scheme suppresses ambient defects (e.g., adsorbed water molecules), which have been suggested to contribute to the hysteresis in bare MoS2/SiO2 devices.29 Therefore, the charge trapping dynamics in our BPFETs are dominated by traps in SiO2, which can be very well described using our TCAD models.29 Second, the alignment of the defect bands in SiO2 with respect to the conduction and valence bands of BP is comparably favorable (see Fig. S5 in the SI). While the impact of the lower defect band is completely negligible, the middle of the upper defect band is above the conduction band of BP. Therefore, only a minor fraction of oxide traps can contribute to charge trapping within the operation V g range of our device. These active defects are relatively close to the lower edge of the upper defect band, where D ot is lower than in the middle of the defect band. As for the possible perspectives of BPFETs, the use of hBN41, 42 as a gate dielectric instead of SiO2 might allow to further minimize D ot, thereby leading to an even better device performance. However, the potential benefit of using hBN as an insulator will depend on the exact location of the defect bands in hBN, which are currently unknown. Unfortunately, although BP/hBN heterostructures have already been successfully fabricated,43 no BP/hBN devices were available for our studies.
The differential energy distributions of the oxide trap density D ot(E) for a T = 95 °C, b T = 130 °C and c T = 165 °C; the measurement frequency f is spaced logarithmically between 5 × 10−4 and 1 Hz. At higher temperatures the D ot(E) dependences are more sensitive to the measurement frequency, while the trap density is larger. d The energy distributions of slow oxide traps (f = 5 × 10−4 Hz) obtained for three different temperatures. Due to thermal activation, the effective trap density becomes larger at higher temperatures. e Comparison of typical D ot values for our BPFETs with literature reports for different technologies.33,34,35,36,37,38,39,40
In conclusion, we have demonstrated that BPFETs with conformal Al2O3 encapsulation can exhibit a stable performance for at least 17 months. This allowed us to perform an accurate energetic mapping of oxide traps with widely distributed time constants. While we have shown that the thermal activation of charge trapping can severely degrade the performance of our BPFETs at elevated temperatures, the obtained values of the oxide trap density are unexpectedly low. They can be several orders of magnitude lower than for MoS2/SiO2 devices and comparable to Si technologies, even though BP is one of the most recently introduced 2D materials. As such, we conclude that a considerable advancement in the technology of next-generation 2D FETs has been obtained, all the more significant owing to the recent breakthrough in epitaxial synthesis of monolayer phosphorene.
Methods
The devices were fabricated on Si/SiO2 substrates with 80 nm thick oxide layer. Few-layer phosphorene flakes were mechanically exfoliated on top of a SiO2 layer from bulk BP (HQ Graphene). Immediately after exfoliation, PMMA A4 was spin-coated and baked at 180 °C. This allowed us to obtain a resist layer for e-beam lithography and also to minimize air-contact and degradation. In order to achieve a better device performance, we selected the thinnest phosphorene flakes with a thickness below 15 nm. This was done using an optical microscope according to color contrast. The source/drain electrode area was created by e-beam lithography using a Carl Zeiss FENEON 40 SEM system. This step was followed by metal evaporation of a 4 nm Ti adhesion promoter layer and 40 nm Au. Right after lift-off in acetone for 2 h, the 25 nm-thick Al2O3 encapsulation layer was grown by atomic layer deposition at 150 °C. We note that before the deposition of the encapsulation layer, bare BP flakes were exposed to the ambient air no longer than 1 h in total.
All our measurements have been performed in a chamber of a Lakeshore vacuum probestation at a pressure of 5 × 10−6–10−5 torr and temperatures from 27 to 165 °C. The I d − V g characteristics of our BPFETs have been measured in both sweep directions using a Keithley-2636A. An elementary loop of our experimental technique consists of measurements using a fixed sweep range V gmin to V gmax and the step voltages V step from the range [1 V…0.01 V] and sampling time t step varied between 0.2 and 500 ms, i.e., the sweep rate S = V step/t step between 0.02 and 5000 V/s. We repeated these loops using either, (1) a fixed V gmin = −20V and V gmax varied between 0 to 20 V in 1 V steps or (2) V gmax = 20V and V gmin from 0 to −20 V in −1 V steps. In the first case we start with a V + sweep followed by a V − sweep, while in the second case we first perform a V − sweep and then proceed with the V + sweep. As a result we obtain two sets of ΔV Hn(f) and two sets of ΔV Hp(f) characteristics which contain the information about the distribution of charged oxide traps with different time constants. The measurement frequency is given as f = 1/(Nt step) with N = 2((V gmax − V gmin)/V step + 1) being the number of voltage step points. In order to capture the impact of the varied edge of the sweep range on the charge trapping dynamics without considerable time delay, in the case of varied V gmax we analyze the ΔV Hn(f) dependences. Conversely, for varied V gmin we consider the ΔV Hp(f) curves, except the case of very narrow sweep ranges, when the hole conduction region can not be accessed. For a more accurate and intuitive evaluation of the hole capture and emission contributions, we split the total ΔV Hn|p(f) dependences into the Δ\(V_{{\rm{Tn|p}}}^ + \)(f) and Δ\(V_{{\rm{Tn|p}}}^ - \)(f) shifts determined relatively to the fast sweep (S = 1000 V/s) I d − V g characteristics which can be considered as weakly perturbed by the hysteresis.
Data availability
All relevant data are available from the authors.
References
Liu, H. et al. Phosphorene: an unexplored 2D semiconductor with a high hole mobility. ACS Nano 8, 4033–4041 (2014).
Wei, Q. & Peng, X. Superior mechanical flexibility of phosphorene and few-layer black phosphorus. Appl. Phys. Lett. 104, 251915 (2014).
Li, L. et al. Black phosphorus field-effect transistors. Nat. Nanotechnol. 9, 372–377 (2014).
Liu, H., Du, Y., Deng, Y. & Peide, D. Semiconducting black phosphorus: synthesis, transport properties and electronic applications. Chem. Soc. Rev. 44, 2732–2743 (2014).
Novoselov, K. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Radisavljevic, B., Whitwick, M. & Kis, A. Integrated circuits and logic operations based on single-layer MoS2. ACS Nano 5, 9934–9938 (2011).
Das, S., Chen, H., Penumatcha, A. & Appenzeller, J. High performance multilayer MoS2 transistors with scandium contacts. Nano. Lett. 13, 100–105 (2012).
Yang, S., Park, S., Jang, S., Kim, H. & Kwon, J.-Y. Electrical stability of multilayer MoS2 field-effect transistor under negative bias stress at various temperatures. Phys. Status Solidi Rapid Res Lett. 8, 714–718 (2014).
Cho, A.-J. et al. Multi-layer MoS2 FET with small hysteresis by using atomic layer deposition Al2O3 as gate insulator. ECS Solid State Lett. 3, Q67–Q69 (2014).
Perello, D. J., Chae, S. H., Song, S. & Lee, Y. H. High-performance n-type black phosphorus transistors with type control via thickness and contact-metal engineering. Nat. Commun. 6, 7809 (2015).
Zhang, J. L. et al. Epitaxial growth of single layer blue phosphorus: a new phase of two-dimensional phosphorus. Nano Lett. 16, 4903–4908 (2016).
Das, S., Demarteau, M. & Roelofs, A. Ambipolar phosphorene field effect transistor. ACS Nano 8, 11730–11738 (2014).
Kim, J.-S. et al. Toward air-stable multilayer phosphorene thin-films and transistors. Sci. Rep. 5, 1–7 (2015).
Zhu, W. et al. Flexible black phosphorus ambipolar transistors, circuits and AM demodulator. Nano Lett. 15, 1883–1890 (2015).
Wood, J. et al. Effective passivation of exfoliated black phosphorus transistors against ambient degradation. Nano Lett. 14, 6964–6970 (2014).
Illarionov, Y. et al. Bias-temperature instability in single-layer graphene field-effect transistors. Appl. Phys. Lett. 105, 143507 (2014).
Guo, Y. et al. Charge trapping at the MoS2-SiO2 interface and its effects on the characteristics of MoS2 metal-oxide-semiconductor field effect transistors. Appl. Phys. Lett. 106, 103109 (2015).
Park, Y., Baac, H., Heo, J. & Yoo, G. Thermally activated trap charges responsible for hysteresis in multilayer mos2 field-effect transistors. Appl. Phys. Lett. 108, 083102 (2016).
Grasser, T. et al. On the microscopic structure of hole traps in pMOSFETs. In IEEE Int. Electron Devices Meet.(IEDM) 21.1.1–2 1.1.4 (IEEE, 2014).
Lee, Y. et al. Fast transient charging at the graphene/SiO2 interface causing hysteretic device characteristics. Appl. Phys. Lett. 98, 183508 (2011).
Qiu, H. et al. Electrical characterization of back-gated Bi-layer MoS2 field-effect transistors and the effect of ambient on their performances. Appl. Phys. Lett. 100, 123104 (2012).
Late, D., Liu, B., Matte, H., Dravid, V. & Rao, C. Hysteresis in single-layer MoS2 field effect transistors. ACS Nano 6, 5635–5641 (2012).
Franco, J. et al. Superior NBTI reliability of SiGe channel pMOSFETs: Replacement gate, FinFETs, and impact of body bias. In IEEE Int. Electron Devices Meet.(IEDM) (IEEE, 2011).
Degraeve, R. et al. Trap spectroscopy by charge injection and sensing (TSCIS): A quantitative electrical technique for studying defects in dielectric stacks. In IEEE Int. Electron Devices Meet.(IEDM) 1–4 (IEEE, 2008).
Illarionov, Y. et al. Energetic mapping of oxide traps in MoS2 field-effect transistors. 2D Mater. 4, 025108 (2017).
Favron, A. et al. Photooxidation and quantum confinement effects in exfoliated black phosphorus. Nat. Mater. 14, 826–832 (2015).
Wang, H., Wu, Y., Cong, C., Shang, J. & Yu, T. Hysteresis of electronic transport in graphene transistors. ACS Nano 4, 7221–7228 (2010).
Cho, K. et al. Electric stress-induced threshold voltage instability of multilayer MoS2 Field effect transistors. ACS Nano 7, 7751–7758 (2013).
Illarionov, Y. et al. The role of charge trapping and MoS2/SiO2 and MoS2/hBN field-effect transistors. 2D Mater. 3, 035004 (2016).
Illarionov, Y. et al. Long-term stability and reliability of black phosphorus field-effect transistors. ACS Nano 10, 9543–9549 (2016).
TU Wien MINIMOS-NT 2.1 User’s Guide, Institut fur Mikroelektronik, Technische Universitat Wien: Austria (2004).
Rzepa, G. et al. Complete extraction of defect bands responsible for instabilities in n and pFinFETs. In IEEE Symp. on VLSI Technol. 208–209 (IEEE, 2016).
Wang, F. & Çelik Butler, Z. An improved physics-based 1/f noise model for deep sub-micron MOSFETs. Solid State Electron. 45, 351–357 (2001).
von Haartman, M., Wu, D., Hellstrom, P., Zhang, S.-L. & Ostling, M. Low-frequency noise in Si0.7Ge0.3 surface channel pMOSFETs with a metal/high-k gate stack. In 17th Int. Conf. Noise and Fluctuations (ICNF) 381–384 (IEEE, 2003).
Simoen, E., Mercha, A., Pantisano, L., Claeys, C. & Young, E. Low-frequency noise behavior of SiO2-HfO2 dual-layer gate dielectric nMOSFETs with different interfacial oxide thickness. IEEE Trans. Electron. Devices 51, 780–784 (2004).
Min, B. et al. Low-frequency noise characteristics of HfSiON gate-dielectric metal-oxide-semiconductor-field-effect transistors. Appl. Phys. Lett. 86, 2102 (2005).
Simoen, E., Veloso, A., Higuchi, Y., Horiguchi, N. & Claeys, C. On the oxide trap density and profiles of 1-nm EOT metal-gate last cmos transistors assessed by low-frequency noise. IEEE Trans. Electron. Devices 60, 3849–3855 (2013).
Renteria, J. et al. Low-frequency 1/f noise in MoS2 transistors: Relative contributions of the channel and contacts. Appl. Phys. Lett. 104, 153104 (2014).
Çelik-Butler, Z. et al. Determination of active oxide trap density and 1/f noise mechanism in RESURF LDMOS transistors. Solid State Electron. 111, 141–146 (2015).
Yuan, L. et al. Low frequency noise and radiation response in the partially depleted SOI MOSFETs with ion implanted buried oxide. Chin. Phys. B 24, 088503 (2015).
Hui, F. et al. On the use of two dimensional hexagonal boron nitride as dielectric. Microelectron. Eng. 163, 119–133 (2016).
Ji, Y. et al. Boron nitride as two dimensional dielectric: Reliability and dielectric breakdown. Appl. Phys. Lett. 108, 012905 (2016).
Gillgren, N. et al. Gate tunable quantum oscillations in air-stable and high mobility few-layer phosphorene heterostructures. 2D Mater. 2, 011001 (2014).
Acknowledgements
The authors thank the EC for the financial support through the FWF grant n° I2606-N30 and also the STREP project MoRV (n° 619234). D.A. acknowledges the partial support of the National Science Foundation (NSF) EAGER grant and the Office of Naval Research (ONR). Yu.Yu.I. is a member of the Mediterranean Institute of Fundamental Physics (MIFP).
Author information
Authors and Affiliations
Contributions
Yu.Yu.I. carried out the measurements, analyzed the experimental data and composed the text. M.W. developed the measurement script and provided technical assistance with the experiments. G.R. an T.K. performed the TCAD simulations. The experiments and simulations were performed at TU Wien under the guidance of T.G. The devices were fabricated at the UT Austin by J.-S.K. under the guidance of D.A. All the authors discussed the results and contributed to the writting of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Illarionov, Y.Y., Waltl, M., Rzepa, G. et al. Highly-stable black phosphorus field-effect transistors with low density of oxide traps. npj 2D Mater Appl 1, 23 (2017). https://doi.org/10.1038/s41699-017-0025-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-017-0025-3
This article is cited by
-
Seeded growth of single-crystal black phosphorus nanoribbons
Nature Materials (2024)
-
Imaging Fermi-level hysteresis in nanoscale bubbles of few-layer MoS2
Communications Materials (2023)
-
Insight into the growth mechanism of black phosphorus
Frontiers of Physics (2023)
-
High-performance junction-free field-effect transistor based on blue phosphorene
npj 2D Materials and Applications (2022)
-
Inorganic nanomaterial lubricant additives for base fluids, to improve tribological performance: Recent developments
Friction (2022)