Introduction

Entanglement is a vital asset in quantum information sciences that can enhance quantum technologies such as communication, cryptography and computing beyond classical limitations1. Such quantum technologies mostly rely on the distribution of entanglement in multipartite settings. Quantification and characterization of entanglement distribution for multipartite systems is well explained through monogamy relation. Briefly, the monogamy explains that if two parties are maximally entangled, then the rest of the parties cannot share any entanglement with them. This monogamy property, for example, plays a role in security analysis of quantum key distribution2 and it can also be used to distinguish quantum channels3.

The concept of monogamy of entanglement was first introduced by Coffman, Kundu and Wootters4–known as CKW inequality. They established the monogamy property for tripartite (A, B, and C) system via an entanglement measure called the concurrence5. Furthermore, the monogamy inequality asserts that the summation of individual entanglement content of subsystem A with subsystem B and with subsystem C is less than or equal to the entanglement of subsystem A with combined subsystem BC. This monogamy relation was then generalized to N-qubit systems6. Later on, monogamy relations for various entanglement measures have been proved, e.g., concurrence4,7,8,9, entanglement of formation6,10,11, negativity9,12,13,14,15, Tsallis-q entanglement16,17,18, and Rényi-q entanglement19,20. The dual of monogamy (polygamy) relation via the concurrence of assistance was proposed to quantify the limitation of distributing bipartite entanglement in multipartite systems21,22. Polygamy relations were established using various entanglement measures, e.g., convex-roof extended negativity13, and Tsallis-q entanglement9,16.

This paper proposes the idea to understand the entanglement distribution in multipartite system via the unified-(q, s) entanglement  \(({{\mathscr{U}}}_{q,s})\).  \({{\mathscr{U}}}_{q,s}\) encompasses several measures of entanglement such as concurrence, Tsallis-q entanglement (Tq -E), Rényi-q entanglement (Rq-E), and entanglement of formation (EOF), as its special cases. However, it does not satisfy the usual monogamy relations and violates monogamy for W-class state23. The monogamy relation of EOF has been not reported yet in a unified fashion. Three tangle based on the squared concurrence also has some flaws for entanglement detection24. This highly motivates us to introduce a general concept of monogamy relations in multiqubit systems, which can overcome these flaws. We propose new monogamy relations for \({{\mathscr{U}}}_{q,s}\). To this end, we first give the analytic formula of  \({{\mathscr{U}}}_{q,s}\) for the region \(q\ge (\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\), 0 ≤ s ≤ 1, and \(qs\le (5+\sqrt{13})/2\). Then, we establish the monogamy relation of multiqubit entangled system based on the squared \({{\mathscr{U}}}_{q,s}\) (SU-(q,s)-E), which encompasses the monogamy relations of EOF, Tq-E, and Rq-E, as special cases. Therefore, the results in this paper provide a unifying framework for monogamy relations in multiqubit systems, covering several previous monogamy results6,16,17,18,19,20,23.

Results

First, we revise the definition of \({{\mathscr{U}}}_{q,s}\) and present the formula with its extended ranges. Then we investigate the monogamy relations for the squared and α ≥ 2 power of  \({{\mathscr{U}}}_{q,s}\). Polygamy relation of \({{\mathscr{U}}}_{q,s}\) for α ≤ 0 is also obtained. We further construct the multipartite entanglement indicator and present some numerical examples.

Unified-(q,s) entanglement

For any bipartite pure state \({|\psi \rangle }_{AB}\), \({{\mathscr{U}}}_{q,s}\) is defined as23

$${{\mathscr{U}}}_{q,s}({|\psi \rangle }_{AB})={(s\mathrm{(1}-q))}^{-1}[{({\rm{tr}}{\rho }_{A}^{q})}^{s}-1],$$
(1)

for (q,s) ≥ 0|q≠1,s≠0, where the state of the subsystem A is obtained by tracing out the subsystem B, i.e., \({\rho }_{A}={{\rm{tr}}}_{B}[{|\psi \rangle }_{AB}\langle \psi |]\).

For any bipartite mixed state ρAB, \({{\mathscr{U}}}_{q,s}\) and \({{\mathscr{U}}}_{q,s}\) of assistance \(({\hat{{\mathscr{U}}}}_{q,s})\) are defined as

$${{\mathscr{U}}}_{q,s}({\rho }_{AB})=\,{\rm{\min }}\sum _{i}\,{p}_{i}{{\mathscr{U}}}_{q,s}({|{\psi }_{i}\rangle }_{AB}),$$
(2)
$${\hat{{\mathscr{U}}}}_{q,s}({\rho }_{AB})=\,{\rm{\max }}\sum _{i}\,{p}_{i}{{\mathscr{U}}}_{q,s}({|{\psi }_{i}\rangle }_{AB}),$$
(3)

where the minimization and maximization are obtained over all pure state decompositions \({\sum }_{i}\,{p}_{i}{|{\psi }_{i}\rangle }_{AB}\langle {\psi }_{i}|\) of ρAB.

The \({{\mathscr{U}}}_{q,s}\) encompasses various entanglement measures depending on the parameters q and s. For example, it converges to Rq-E, Tq-E, and EOF when s → 0, s → 1, and q → 1, respectively.

Refining the analytical formula for \({{\mathscr{U}}}_{q,s}\)

For any two-qubit mixed state ρAB, concurrence \({\mathscr{C}}\) is given as5

$${\mathscr{C}}({\rho }_{AB})=\,{\rm{\max }}\{\mathrm{0,}{\mu }_{1}-{\mu }_{2}-{\mu }_{3}-{\mu }_{4}\},$$
(4)

where μi are the decreasing eigenvalues of \(\sqrt{{\rho }_{AB}({\sigma }_{{\rm{y}}}\otimes {\sigma }_{{\rm{y}}}){\rho }_{AB}^{\ast }({\sigma }_{{\rm{y}}}\otimes {\sigma }_{{\rm{y}}})}\), and σy denotes the Pauli-y operator.

The analytic relationship between \({{\mathscr{U}}}_{q,s}\) and concurrence of a bipartite state ρAB for 1 ≥ s ≥ 0 and 3/s ≥ q ≥ 1 has been unveiled as follows23:

$${{\mathscr{U}}}_{q,s}({\rho }_{AB})={f}_{q,s}({\mathscr{C}}({\rho }_{AB})),$$
(5)

where

$${f}_{q,s}(x)=\frac{{({\eta }_{+}^{q}+{\eta }_{-}^{q})}^{s}-{2}^{qs}}{s(1-q){2}^{qs}}$$
(6)

with \({\eta }_{\pm }=(1\pm \sqrt{1-{x}^{2}})\).

The analytic formula (5) holds until the fq,s(x) in (6) is monotonically increasing and convex for any q and s value23. The monotonicity and convexity follow from the fact that ∂fq,s(x)/∂x ≥ 0 for all q ≥ 0 and ∂2fq,s(x)/∂x2 ≥ 0 for 1 ≥ s ≥ 0 and 3/s ≥ q ≥ 123.

In the Methods section, we prove that \({f}_{q,s}({\mathscr{C}})\) is a convex function of \({\mathscr{C}}\) for the region \(q\ge (\sqrt{9{s}^{2}-24s+28}-\)\((2+3s))\)/(2(2 − 3s)), 0 ≤ s ≤ 1, and \(qs\le (5+\sqrt{13})/2\). Therefore, we have an extended (q, s)-region with \(q\ge (\sqrt{9{s}^{2}-24s+28}-(2+3s))\)/(2(2 − 3s)), 0 ≤ s ≤ 1, and \(qs\le (5+\sqrt{13})/2\), where the second-order derivative of fq,s(x) is nonnegative. Consequently, the analytic formula of unified-(q, s) entanglement (5) now holds for

$${\mathscr{R}}=\{(q,s)|(\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\le q\le (5+\sqrt{13})/2s,0\le s\le 1\}.$$

Monogamy relation for SU-(q,s)-E in multiqubit systems

The main result of the paper is the general monogamy inequality of SU-(q,s) -E \({{\mathscr{U}}}_{q,s}^{2}\) for an arbitrary multipartite qubit mixed state (see Theorem 1), i.e.,

$${{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})-{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}})-{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{2}})-\cdots -{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{N-1}})\ge \mathrm{0,}$$
(7)

where \({{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\) quantifies entanglement in the partition A|B1B2 … BN−1, and \({{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{i}})\) quantifies the bipartite entanglement between A and Bi. Before approaching towards our main relations, we propose two propositions, whose proofs are given in Methods section. These propositions are used for establishing the monogamy relation of \({{\mathscr{U}}}_{q,s}\).

We define

$${{\mathscr{U}}}_{q,s}({|\psi \rangle }_{AB})={g}_{q,s}({{\mathscr{C}}}^{2}({|\psi \rangle }_{AB}))=\frac{{({(1+\sqrt{1-{{\mathscr{C}}}^{2}})}^{q}+{(1-\sqrt{1-{{\mathscr{C}}}^{2}})}^{q})}^{s}-{2}^{qs}}{(1-q)s{2}^{qs}}.$$
(8)

Proposition 1. SU-(q,s)-E \({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) with \((q,s)\in {\mathcal R} \) varies monotonically as a function of squared concurrence \({{\mathscr{C}}}^{2}\).

Proposition 2. SU-(q,s)-E \({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) with \((q,s)\in {\mathcal R} \) is convex as a function of squared concurrence \({{\mathscr{C}}}^{2}\).

In the succeeding theorem, we will establish the monogamy inequity of \({{\mathscr{U}}}_{q,s}^{2}\) for N-qubit mixed state ρAB1B2 … BN−1.

Theorem 1. SU-(q,s)-E holds the following monogamy inequality for an arbitrary multi-qubit mixed state ρAB1B2…BN−1:

$${{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\ge {{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}})+{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{2}})+\cdots +{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{N-1}}),$$
(9)

with \((q,s)\in {\mathcal R} \).

Proof. The formula of \({{\mathscr{U}}}_{q,s}\) (5) cannot be applied to \({{\mathscr{U}}}_{q,s}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\) since the subsystem B1B2 … BN−1 is not a logic qubit. However, We can apply the convex roof extension formula (2) of the pure state entanglement. Let \({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}={\sum }_{k}\,{p}_{k}{|{\psi }_{k}\rangle }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}\langle {\psi }_{k}|\) be the optimal decomposition that minimizes \({{\mathscr{U}}}_{q,s}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\). Then we have

$$\begin{array}{rcl}{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}) & = & {[\sum _{k}{p}_{k}{{\mathscr{U}}}_{q,s}({|{\psi }_{k}\rangle }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})]}^{2}\\ & \mathop{=}\limits^{({\rm{a}})} & {[\sum _{k}{p}_{k}{f}_{q,s}({\mathscr{C}}({|{\psi }_{k}\rangle }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}))]}^{2}\\ & \mathop{\ge }\limits^{({\rm{b}})} & {[{f}_{q,s}(\sum _{k}{p}_{k}{\mathscr{C}}({|{\psi }_{k}\rangle }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}))]}^{2}\\ & \mathop{\ge }\limits^{({\rm{c}})} & {[{f}_{q,s}({\mathscr{C}}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}))]}^{2}={g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})),\end{array}$$
(10)

where (a) follows from the pure state formula of the \({{\mathscr{U}}}_{q,s}\) and takes the \({f}_{q,s}({\mathscr{C}})\) as a function of concurrence \({\mathscr{C}}\) for \((q,s)\in {\mathcal R} \); (b) is due to the fact that \({f}_{q,s}({\mathscr{C}})\) is a convex function of concurrence for \((q,s)\in {\mathcal R} \); and (c) is due to the convexity of concurrence for mixed states.

$$\begin{array}{lll}{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}) & \mathop{\ge }\limits^{({\rm{d}})} & {g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}}))\\ & \mathop{\ge }\limits^{({\rm{e}})} & {g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{1}})+{{\mathscr{C}}}^{2}({\rho }_{A{B}_{2}})+\cdots +{{\mathscr{C}}}^{2}({\rho }_{A{B}_{N}-1}))\\ & \mathop{\ge }\limits^{({\rm{f}})} & {g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{1}}))+{g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{2}}))+\cdots +{g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{A{B}_{N-1}}))\\ & = & {{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{1}})+{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{2}})+\cdots +{{\mathscr{U}}}_{q,s}^{2}({\rho }_{A{B}_{N-1}})\end{array}$$

where (d) is from (10); (e) and (f) are due to Propositions 1 and 2, respectively.\(\square \)

Remark 1. SU-(q,s)-E provides us the broad class of monogamy inequalities and recovers the monogamy relations for squared EOF, Tq-E and Rq-E for different values of q and s. Specifically, (9) can be reduced to the following monogamy relations:

  1. i.

    Squared EOF6,10, for q → 1

    $${{\mathscr{E}}}_{f}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\ge {{\mathscr{E}}}_{f}^{2}({\rho }_{A{B}_{1}})+{{\mathscr{E}}}_{f}^{2}({\rho }_{A{B}_{2}})+\cdots +{{\mathscr{E}}}_{f}^{2}({\rho }_{A{B}_{N-1}}),$$
    (11)
  2. ii.

    Squared Rq-E19,20, for s → 0

    $${ {\mathcal R} }_{q}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\ge { {\mathcal R} }_{q}^{2}({\rho }_{A{B}_{1}})+{ {\mathcal R} }_{q}^{2}({\rho }_{A{B}_{2}})+\cdots +{ {\mathcal R} }_{q}^{2}({\rho }_{A{B}_{N-1}}),$$
    (12)
  3. iii.

    Squared Tq-E16,17,18, for s → 1

$${{\mathscr{T}}}_{q}^{2}({\rho }_{A{B}_{1}{B}_{2}\cdots {B}_{N-1}})\ge {{\mathscr{T}}}_{q}^{2}({\rho }_{A{B}_{1}})+{{\mathscr{T}}}_{q}^{2}({\rho }_{A{B}_{2}})+\cdots +{{\mathscr{T}}}_{q}^{2}({\rho }_{A{B}_{N-1}})\mathrm{.}$$
(13)

The αth power \({{\mathscr{U}}}_{q,s}\) monogamy relation

In this subsection, we establish the αth power \({{\mathscr{U}}}_{q,s}\) based general monogamy and polygamy inequalities.

Theorem 2. For an arbitrary tripartite qubit state ρA1A2A3, we have

$${{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}{A}_{3}})\ge {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{3}}),$$
(14)

with α ≥ 2 and \((q,s)\in {\mathcal R} \).

Proof. According to the monogamy relation given in (9)

$${{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}{A}_{3}})\ge {{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}}),$$

for an arbitrary tripartite state ρA1A2A3 with \(q\ge (\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\), 0 ≤ s ≤ 1 and \(qs\le (5+\sqrt{13})/2\). If \({\rm{\min }}\{{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}}),{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}})\}=0\), the inequality (14) obviously holds. Without any loss of generality, we assume that \({{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})\ge {{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}})\). Then, we have

$$\begin{array}{ccc}{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}{A}_{3}}) & \ge & {({{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}}))}^{\frac{\alpha }{2}}\\ & \mathop{\ge }\limits^{({\rm{a}})} & {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})(1+{(\frac{{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}})}{{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})})}^{\frac{\alpha }{2}})\\ & = & {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{3}}),\end{array}$$

where (a) comes from the algebraic inequality 1 + βγ ≤ (1 + β)γ for β ≤ 1, and γ ≥ 1.\(\square \)

Theorem 3. The αth power \({{\mathscr{U}}}_{q,s}\) satisfies the following polygamy relation for any tripartite state

$${{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}{A}_{3}}) < {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{3}}),$$
(15)

with α ≤ 0 and \((q,s)\in {\mathcal R} \).

Proof. For any tripartite state ρA1A2A3 with α ≤ 0, we have

$$\begin{array}{ccc}{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}{A}_{3}}) & \le & {({{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}}))}^{\frac{\alpha }{2}}\\ & \mathop{ < }\limits^{({\rm{a}})} & {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})(1+{(\frac{{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{3}})}{{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{2}})})}^{\frac{\alpha }{2}})\\ & = & {{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{2}})+{{\mathscr{U}}}_{q,s}^{\alpha }({\rho }_{{A}_{1}{A}_{3}}),\end{array}$$

where (a) follows from 1 + βγ > (1 + β)γ for β > 0, and γ ≤ 0.\(\square \)

Remark 2. Theorem 2 and Theorem 3 have established the monogamy and dual monogamy inequalities for the αth power \({{\mathscr{U}}}_{q,s}\) for α ≥ 2 and α ≤ 0, respectively in a tripartite scenario. These relations can be generalized for multiqubit systems by using induction and simple algebraic inequalities.

Multipartite entanglement indicators based on the SU-(q, s)-E

From monogamy relation (9) of SU-(q,s)-E, we build a multipartite entanglement indicator that can be utilized to detect entanglement in the N-qubit state ρA1A2 … AN. The indicator \({{\mathscr{J}}}_{q,s}\) is defined as

$${{\mathscr{J}}}_{q,s}({\rho }_{{A}_{1}{A}_{2}\cdots {A}_{N}})=\,min\sum _{i}\,{p}_{i}{{\mathscr{J}}}_{q,s}({|{\psi }_{i}\rangle }_{{A}_{1}|{A}_{2}\cdots {A}_{N}}),$$
(16)

where the minimization is performed over all pure state decompositions of ρA1A2 … AN. This indicator essentially originates from the convex-roof of the pure state indicator \({{\mathscr{J}}}_{q,s}({|\psi \rangle }_{{A}_{1}|{A}_{2}\cdots {A}_{N}})={{\mathscr{U}}}_{q,s}^{2}({|\psi \rangle }_{{A}_{1}|{A}_{2}\cdots {A}_{N}})-{\sum }_{i\mathrm{=2}}^{N}\,{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{i}})\). Then it becomes

$${{\mathscr{J}}}_{q,s}({\rho }_{{A}_{1}{A}_{2}\cdots {A}_{N}})={{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}|{A}_{2}\cdots {A}_{N}})-\mathop{\sum }\limits_{i=2}^{N}\,{{\mathscr{U}}}_{q,s}^{2}({\rho }_{{A}_{1}{A}_{i}}),$$
(17)

which quantifies the residual entanglement in the system.

Following examples demonstrate the universal nature of \({{\mathscr{J}}}_{q,s}\) as an effective entanglement indicator. In particular, we evaluate (17) for the W-state, and for the state which is in the superposition of Greenberger-Horne-Zeilinger (GHZ) and W states. The nonzero values of \({{\mathscr{J}}}_{q,s}\) in these examples asserts its validity as a genuine entanglement indicator.

Example 1. An N-qubit W-state is defined as

$$|{W}_{N}\rangle =\frac{1}{\sqrt{N}}(|10\cdots 0\rangle +|01\cdots 0\rangle +\cdots +|0\cdots 01\rangle )\mathrm{.}$$
(18)

The indicator for the N-qubit W-class state can be written as

$${{\mathscr{J}}}_{q,s}(|{W}_{N}\rangle )={g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{{A}_{1}|{A}_{2}\cdots {A}_{N}}))-(N-1){g}_{q,s}^{2}({{\mathscr{C}}}^{2}({\rho }_{{A}_{1}{A}_{2}})),$$
(19)

where \({{\mathscr{C}}}^{2}({\rho }_{{A}_{1}|{A}_{2}\cdots {A}_{N}})=4(N-1)/{N}^{2}\) and \({{\mathscr{C}}}^{2}({\rho }_{{A}_{1}{A}_{2}})=4/{N}^{2}\). Via the established monogamy relation of the squared concurrence, the three tangle \({{\mathscr{J}}}_{{\mathscr{C}}}\) (genuine tripartite entanglement measure) is defined as4

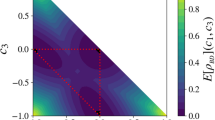
$${{\mathscr{J}}}_{{\mathscr{C}}}^{2}({|\psi \rangle }_{ABC})={{\mathscr{C}}}^{2}({\rho }_{A|BC})-{{\mathscr{C}}}^{2}({\rho }_{AB})-{{\mathscr{C}}}^{2}({\rho }_{AC})\mathrm{.}$$
(20)

The three tangle cannot detect the tripartite entangled W-state4. However, the indicator \({{\mathscr{J}}}_{q,s}\) efficiently detects the entanglement in this state. We plot the indicator as a function of (q,s) for the four and five qubit W-state in Fig. 1. The indicator has nonzero values when entanglement is present in the system.

Figure 1
figure 1

The indicator \({{\mathscr{J}}}_{q,s}\) results for W-state with (a) N = 4, and (b) N = 5. The solid black line shows the boundary qs = 4.302. Non zero values show the residual entanglement in the system.

Full size image

Example 2. We consider a superposition state of GHZ state and the W-state

$${|\psi \rangle }_{ABC}=\sqrt{p}|GHZ\rangle -\sqrt{1-p}|W\rangle ,$$
(21)

where \(|GHZ\rangle =\frac{1}{\sqrt{2}}({|0\rangle }^{\otimes 3}+{|1\rangle }^{\otimes 3})\) and \(|W\rangle =\frac{1}{\sqrt{3}}(|001\rangle +|010\rangle +|100\rangle ).\)

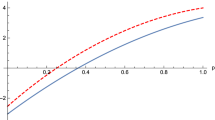
The three tangle of \({|\psi \rangle }_{ABC}\) is \({{\mathscr{J}}}_{{\mathscr{C}}}({|\psi \rangle }_{ABC})=\mathrm{(9}{p}^{2}-8\sqrt{6}\sqrt{p{\mathrm{(1}-p)}^{3}})/9\) and is zero for p = 0, and p = 0.6276,24. This shows some flaw in the entanglement indicator. In this scenario, \({{\mathscr{J}}}_{q,s}\) multipartite entanglement indicator shown in (17) is used. The value of \({{\mathscr{J}}}_{q,s}({|\psi \rangle }_{ABC})\) is calculated through the analytic formula of the \({{\mathscr{U}}}_{q,s}\) for bipartite states. There is no need for convex-roof for the pure state. In Fig. 2, we draw the comparison between the \({{\mathscr{J}}}_{{\mathscr{C}}}\) and \({{\mathscr{J}}}_{q,s}\). We can see that \({{\mathscr{J}}}_{q,s}\) is positive for all values of p.

Figure 2
figure 2

The indicator \({{\mathscr{J}}}_{q,s}\) for superposition of GHZ and W-state with q = 1.8, s = 0.8 (dotted green line), q = 1.4, s = 0.6 (dashed red line), and q = 1.1, s = 0.4 (solid blue line). The three tangle \({{\mathscr{J}}}_{{\mathscr{C}}}\) of \({|\psi \rangle }_{ABC}\) is also shown with dashdotted black line. \({{\mathscr{J}}}_{q,s}\) is positive for these value of q and s, but \({{\mathscr{J}}}_{q,s}^{2}\) is zero for p = 0, and p = 0.627.

Full size image

Discussion

Unified-(q,s) entanglement is a two-parameter class of well defined bipartite entanglement measures. The generalized analytic formula of \({{\mathscr{U}}}_{q,s}\) has been proved for the region \((q,s)\in {\mathcal R} \), which encompasses EOF5, Tsallis-q entanglement16,17,18 and Renyi-q entanglement19,25 as its special cases. We have investigated the monogamy relation for SU-(q,s)-E, which classifies the entanglement distribution in multipartite systems. The monogamy relation of SU-(q,s)-E enables us to construct an indicator, which overcomes all known flaws and detects genuine multipartite entanglement better than previously known indicators. This superior performance in the detection of multiqubit states is exemplified on W-class states and compared with concurrence based entanglement indicator. The established monogamy relation gives the nontrivial and computable lower bound for the \({{\mathscr{U}}}_{q,s}\). Furthermore, we also proved the αth power \({{\mathscr{U}}}_{q,s}\) based general monogamy and polygamy relations. In summary, the results in this paper provide the unified monogamy relations of multipartite entanglement, covering several previous results as its special cases.

Methods

\({f}_{q,s}({\mathscr{C}})\) is a convex function of the concurrence \({\mathscr{C}}\)

We prove the convexity of fq,s(x) in the extended region \(q\ge (\sqrt{9{s}^{2}-24s+28}-(2+3s))\)/(2(2 − 3s)), 0 ≤ s ≤ 1, and \(qs\le (5+\sqrt{13})/2\), which was previously shown for the region 1 ≥ s ≥ 0 and 3/s ≥ q ≥ 1. We consider the second-order derivative of fq,s(x) for 1 > q > 0 and qs ∈ (3, 5), respectively.

For the region 0 < q < 1, we graphically analyze the solution of \({\partial }^{2}{{\mathscr{U}}}_{q,s}({\mathscr{C}})/\partial {x}^{2}=0\). It can be shown that for fixed s ∈ [0,1], the value of x to keep the second derivative nonnegative increases monotonically with q18,25. Therefore, the critical point exists under the limit x → 1. We apply limit x → 1 to obtain the critical point of q. After applying the limit and some simplification, we have

$$-\frac{{2}^{s-qs}q(3+{q}^{2}(3s-2)-q(3s+2))}{3}=0,$$
(22)

which gives the critical point is \({q}_{\ast }=(\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\) with 0 ≤ s ≤ 1 for the region 0 < q < 1. The second-order derivative is always nonnegative when \(q > {q}_{\ast }\).

For qs ∈ (3, 5), we select qs ≤ 4.302 because when s → 1, fq,s(x) approaches to the Tsallis entropy for which the second derivative is known to be nonnegative for q ≤ 4.30218. For the analytical proof, we define a new range of s on the basis of this constraint, that is, 0 ≤ s ≤ min{4.302/q,1}. We enforce this constraint by substituting s = 4.302/q in the expression for the second derivative of fq,s(x). In the following, we prove that the second derivative is nonnegative for q ≥ 4.302. The second derivative of fq,s(x) after its simplification is

$$\begin{array}{ccc}\frac{{{\rm{\partial }}}^{2}{f}_{q,s}(x)}{{\rm{\partial }}{x}^{2}} & \ge & (q-4.302){x}^{2}\sqrt{1-{x}^{2}}{({B}^{q-1}-{A}^{q-1})}^{2}\\ & & +({A}^{q}+{B}^{q})[({B}^{q-1}-{A}^{q-1})-{x}^{2}\sqrt{1-{x}^{2}}(q-1)({A}^{q-2}+{B}^{q-2})],\end{array}$$
(23)

where \(A=(1-\sqrt{1-{x}^{2}})\) and \(B=(1+\sqrt{1-{x}^{2}})\). First, we apply the binomial expansion on Aq−1 and Bq−1 to write

$$({B}^{q-1}-{A}^{q-1})\ge 2(q-1)\sqrt{1-{x}^{2}}.$$
(24)

Substituting (24) into (23), we get

$$\begin{array}{ccc}\frac{{{\rm{\partial }}}^{2}{f}_{q,s}(x)}{{\rm{\partial }}{x}^{2}} & \ge & (q-4.302){x}^{2}\sqrt{1-{x}^{2}}{(2(q-1)\sqrt{1-{x}^{2}})}^{2}\\ & & +\sqrt{1-{x}^{2}}({A}^{q}+{B}^{q})(q-1)[2-{x}^{2}({A}^{q-2}+{B}^{q-2})].\end{array}$$
(25)

Using the inequality of arithmetic and geometric, i.e., \(x+y\ge 2\sqrt{xy}\), we obtain

$$\begin{array}{rcl}{A}^{q-2}+{B}^{q-2}\ge 2\sqrt{{(AB)}^{q-2}} & = & 2{Z}^{q-2},\\ {A}^{q}+{B}^{q}\ge 2\sqrt{{(AB)}^{q}} & = & 2{Z}^{q},\end{array}$$
(26)

where AB = Z2. Substituting (26) in (23) and after some manipulations, we finally obtain the inequality:

$$\frac{{{\rm{\partial }}}^{2}{f}_{q,s}(x)}{{\rm{\partial }}{x}^{2}}\ge 4(q-1)\sqrt{1-{x}^{2}}[{x}^{2}\sqrt{1-{x}^{2}}(q-4.302)(q-1)+{x}^{q}(1-{x}^{q})].$$
(27)

Now we can see that if q ≥ 4.302 then (27) is positive and the upper constraint qs ≤ 4.302 is satisfied. The second derivative is nonnegative for qs ≤ 4.302 when 0 ≤ s ≤ 1.

\({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) is an increasing monotonic function of the squared concurrence \({{\mathscr{C}}}^{2}\)

Note that we can rewrite the Eq. (5) as

$${{\mathscr{U}}}_{q,s}({|\psi \rangle }_{AB})={g}_{q,s}({{\mathscr{C}}}^{2}({|\psi \rangle }_{AB})),$$
(28)

where

$${g}_{q,s}(x)=\frac{{({\beta }_{+}^{q}+{\beta }_{-}^{q})}^{s}-{2}^{qs}}{(1-q)s{2}^{qs}}$$
(29)

where \({\beta }_{\pm }=(1\pm \sqrt{1-x})\). We investigate the monotonicity of \({g}_{q,s}^{2}(x)\), since the SU-(q,s)-E is a monotonically increasing function of \({{\mathscr{C}}}^{2}\) if dgq,s2(x)/dx > 0 with \(x={{\mathscr{C}}}^{2}\). After some calculation, we have

$$\frac{{\rm{\partial }}{g}_{q,s}^{2}(x)}{{\rm{\partial }}x}=M{2}^{-2qs}(-{2}^{qs}+{({F}^{q}+{E}^{q})}^{s})[\frac{q{s}^{2}{({F}^{q}+{(E)}^{q})}^{s-1}({F}^{q-1}-{E}^{q-1})}{\sqrt{1-x}}],$$
(30)

where M = 1/(q−1)2, \(E=\mathrm{(1}+\sqrt{1-x})\), \(F=\mathrm{(1}-\sqrt{1-x})\). The derivative (30) is non-negative for q ≥ 0 and 0 ≤ x ≤ 1. Thus \({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) is a monotonically increasing function.

\({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) is a convex function of the squared concurrence \({{\mathscr{C}}}^{2}\)

The SU-(q,s)-E is convex in \({{\mathscr{C}}}^{2}\) when the second order derivative \({{\rm{\partial }}}^{2}{{\mathscr{U}}}_{q,s}^{2}(x)/{\rm{\partial }}{x}^{2}\)  ≥ 0 where \(x={{\mathscr{C}}}^{2}\). We define function,

$${Z}_{q,s}(x)=\frac{{{\rm{\partial }}}^{2}{g}_{q,s}^{2}(x)}{{\rm{\partial }}{x}^{2}}$$
(31)

on the domain \(D=\{(x,s,q)\mathrm{|0}\le x\le \mathrm{1,0}\le s\le \mathrm{1,}(\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\le q\le \mathrm{4.302/}s\}\).

After some calculation, we have

$${Z}_{q,s}(x)=q{s}^{2}{2}^{-2qs}M{A}^{s-2}\,[\frac{\{A({2}^{qs}-{A}^{s})(B-(q-1)\sqrt{1-x}({F}^{-2+q}+{E}^{-2+q}))\}+{B}^{2}\sqrt{1-x}\{q(1-s){2}^{qs}+q(2s-1){A}^{s}\}}{2{(1-x)}^{3/2}}]$$
(32)

where A = (Fq + Eq) and B = (Eq−1 − Fq−1).

The intermediate value theorem states that if a continuous function has values of opposite sign inside a domain, then it has a root in that domain. The function Zq,s(x) is continuous on the domain D. We divide D into two sub domains,

$${D}_{1}=\{(x,s,q)\mathrm{|0}\le x\le \mathrm{1,}\,0\le s\le \mathrm{1,}(\sqrt{9{s}^{2}-24s+28}-(2+3s))/(2(2-3s))\le q\le 1\},$$

and

$${D}_{2}=\{(x,s,q)|0\le x\le 1,0\le s\le 1,1\le q\le 4.302/s\}.$$

We plot the solution of Zq,s(x) = 0 for different values of x. As shown in Fig. 3, no root of Zq,s(x) exists inside the domain D. Thus, all values of Zq,s(x) on the domain D have the same sign. This means that if Zq,s is positive for any value of x in D, then it is positive on the entire domain D. We have plotted the function Zq,s(x) on the domain D in Fig. 4 for x → 1. The function Zq,s(x) is positive on the domain D. This means that the second derivative is positive, therefore \({g}_{q,s}^{2}(x)\) is convex on the domain D. Therefore, \({g}_{q,s}^{2}({{\mathscr{C}}}^{2})\) is convex function of the squared concurrence \({{\mathscr{C}}}^{2}\).

Figure 3
figure 3

Domain (a) D1, and (b) D2 are shown as shaded region. Solid black lines show the domain boundary and blue, green, and red lines indicate the roots of Zq,s(x) for different values of x.

Full size image
Figure 4
figure 4

The positivity of Zq,s(x) for x → 1 on the domain (a) D1, and (b) D2.

Full size image