Introduction

When a heavier fluid is supported by a lighter fluid against gravity, the equilibrium is unstable to any perturbations of the interface. For if a parcel of heavier fluid is displaced downward with an equal volume of lighter fluid displaced upwards, the potential energy of the configuration is lower than that in the initial state, and the process goes on. This instability is called the Rayleigh-Taylor Instability (RTI)1. In addition to neutral fluids, RTI also plays an important role in space and laboratory plasmas2,3,4,5,6.

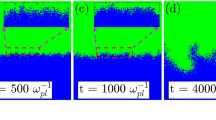
For the neutral fluid, the momentum equation is \(\frac{\partial (\rho {\bf{V}})}{\partial t}=\rho {\bf{g}}-\nabla p\), where ρ, V, g, p is the plasma density, the plasma bulk velocity, the gravity acceleration and the thermal pressure, respectively. In equilibrium state ρg = ∇p. The heavier fluids are supported by lighter fluids through pressure gradient in equilibrium state. For plasma in magnetic field, the momentum equation is \(\frac{\partial (\rho {\bf{V}})}{\partial t}=\frac{1}{c}{\bf{J}}\times {\bf{B}}+\rho {\bf{g}}-\nabla p\), where c, J, B is the light speed, electric current and magnetic field strength, respectively. In equilibrium state \(\rho {\bf{g}}=\nabla p-\frac{1}{c}{\bf{J}}\times {\bf{B}}\). The heavier fluids are supported by lighter fluids through pressure gradient and the J × B force in equilibrium state. The intuitive physical description of magnetic Rayleigh-Taylor instability (MRTI) in some textbooks7 is generally considered to be (Fig. 1): In equilibrium state a net current flows in in the horizontal direction and the current is proportional to the plasma density. There is thus a divergence, and charge will pile up on the edges of the small initial perturbation (charge accumulation). As a result, perturbation electric fields build up in the directions shown. These fields in turn cause an upward (downward) drift in the region where the density is low (high). Lower (higher) density plasma is therefore advected upward (downward), creating a larger perturbation, and the system is unstable. In the above physical description charge accumulation is the cause for the growth of RTI. However, in calculating the linear growth rate of magnetic Rayleigh-Taylor instability (MRTI), the displacement current term in the Maxwell’s equations is ignored8,9. When the displacement current term in the Maxwell’s equations is ignored, take the divergence of the Ampère’s circuital law without Maxwell’s addition shows that the current is always continuous. Which means the contribution of charge accumulation to the growth of MRTI is totally ignored. In this paper, we derived the expression of the linear growth rate of MRTI when charge accumulation is considered and discussed under what circumstances the displacement current can be ignored.

Figure 1
figure 1

Schematic diagram of the MRTI.

Full size image

Assume a bundle of stratified plasma ρ = ρ(y) immersed in a magnetic field B (0, 0, B) and a gravity field g (0, −g, 0) (Fig. 1). To analyze the instability of the system, the relevant magnetohydrodynamic (MHD) equations and Maxwell’s equations written in Gaussian unit are:

$$\frac{\partial (\rho {\bf{V}})}{\partial t}=\frac{1}{c}{\bf{J}}\times {\bf{B}}+\rho {\bf{g}}-\nabla p$$
(1)
$$\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho {\bf{V}})=0$$
(2)
$$\frac{\partial {\bf{E}}}{\partial t}=-\,4\pi {\bf{J}}+c\nabla \times {\bf{B}}$$
(3)
$$\nabla \cdot {\bf{B}}=0$$
(4)
$$\nabla \cdot {\bf{E}}=4\pi {\rho }_{c}$$
(5)
$$\nabla \cdot {\bf{J}}=-\,\frac{\partial {\rho }_{c}}{\partial t}$$
(6)

where V, ρ, c, J, B, p, E, ρc are the velocity of fluid element, plasma mass density, light speed, electric current density, magnetic field, thermal pressure, electric field, charge density, respectively.

The following derivation process of the linear growth rate of stratified plasma in a horizontal magnetic field in this manuscript was similar to that of Sharma et al.10 and Wu et al.11, except that charge conservation equation (Eq. (6)) instead of the current continuity equation was used in the derivation process. Form the momentum equation (Eq. (1)), one can see that the three term on the right side of the equation was equivalent. If charge accumulation effects considered, the J × B term will affect the linear growth rate of magnetic Rayleigh-Taylor instability.

To examine the stability of the system, we assume the following perturbation in physical quantities

$$\begin{array}{c}\rho ={\rho }^{0}+{\rho }^{1}\,p={p}^{0}+{p}^{1}\,{\bf{B}}={{\bf{B}}}^{0}+{{\bf{B}}}^{1}\,{\bf{J}}={{\bf{J}}}^{0}+{{\bf{J}}}^{1}\,{\bf{V}}={{\bf{V}}}^{0}+{{\bf{V}}}^{1}{{\bf{V}}}^{0}=0\\ {\bf{E}}={{\bf{E}}}^{0}+{{\bf{E}}}^{1}\,{{\bf{E}}}^{0}=0.\end{array}$$

In the above equations, quantities with superscripts 0 and 1 denote equilibrium and perturbation quantities, respectively.

Assuming perturbations are in the form

$$\psi \propto \psi (y){e}^{i(kx-\omega t)}$$
(7)

where ω is the frequency of the perturbation, k is the wave number.

Linearizing the Eq. (1), we get

$${\rho }^{0}\frac{\partial {\bf{V}}}{\partial t}=\frac{1}{c}{{\bf{J}}}^{0}\times {{\bf{B}}}^{1}+\frac{1}{c}{{\bf{J}}}^{1}\times {{\bf{B}}}^{0}+{\rho }^{1}{\bf{g}}-\nabla {p}^{1}$$
(8)

z · ∇× Eq. (8) yields

$$-\,i\omega (ik{\rho }^{0}{V}_{y}-\frac{\partial }{\partial y}({\rho }^{0}{V}_{x}))=-\,ik{\rho }^{1}g-\frac{1}{c}(\nabla \cdot {{\bf{J}}}^{1}){B}^{0}$$
(9)

where z is the unit vector in z direction.

From Eqs (5) and (6), we get

$$\nabla \cdot {{\bf{J}}}^{1}=-\,\frac{\partial {\rho }_{c}}{\partial t}=\frac{\partial {\rho }_{c}^{b}}{\partial t}=\frac{{\rm{1}}}{{\rm{4}}\pi }\nabla \cdot (\frac{\partial {\bf{E}}}{\partial t})$$
(10)

where ρc (\({\rho }_{c}^{b}\)) is the charge accumulation in (outside) the fluid element.

Substituting Eq. (10) in Eq. (9) we get

$$-\,i\omega (ik{\rho }^{0}{V}_{y}-\frac{\partial }{\partial y}({\rho }^{0}{V}_{x}))=-\,ik{\rho }^{1}g-\frac{1}{{\rm{4}}\pi c}\omega k{E}_{x}{B}^{0}.$$
(11)

Supposing that the plasma is incompressible

$$\nabla \cdot {\bf{V}}=0$$
(12)

we get the following equation

$${V}_{x}=\frac{i}{k}\frac{\partial {V}_{y}}{\partial y}.$$
(13)

From the linearized continuity equation

$$\frac{\partial {\rho }^{1}}{\partial t}+{\bf{V}}\cdot \nabla {\rho }^{0}=0$$
(14)

We get

$${\rho }^{1}=\frac{1}{iw}\frac{\partial {\rho }^{0}}{\partial y}{V}_{y}.$$
(15)

Form the relation cE + V × B = 0 we get

$${E}_{x}=-\,\frac{1}{c}{V}_{y}{B}^{0}$$
(16)

Substituting the Eqs (13) and (16) into the Eq. (11), we get

$${\rho }^{0}\frac{{\partial }^{2}{V}_{y}}{\partial {y}^{2}}+\frac{\partial {\rho }^{0}}{\partial y}\frac{\partial {V}_{y}}{\partial y}-{k}^{2}({\rho }^{0}+\frac{g}{{\omega }^{2}}\frac{\partial {\rho }^{0}}{\partial y}-\frac{{\rm{1}}}{{\rm{4}}\pi }\frac{{B}^{{0}^{2}}}{{c}^{2}}){{\rm{V}}}_{{\rm{y}}}=0$$
(17)

Assume the initial plasma density has exponential dependence on y

$${\rho }^{0}(y)={\rho }^{0}{e}^{\frac{y}{s}}$$
(18)

where s is a constant, Eq. (17) can be written as

$$\frac{{\partial }^{2}{V}_{y}}{\partial {y}^{2}}+\frac{1}{s}\frac{\partial {V}_{y}}{\partial y}-{k}^{2}(1+\frac{g}{s{\omega }^{2}}-\frac{{V}_{A}^{2}}{{c}^{2}}){{\rm{V}}}_{{\rm{y}}}=0$$
(19)

where \({V}_{A}^{2}=\frac{{B}^{{0}^{2}}}{4\pi {\rho }^{0}}\) is the square of the nominal Alfvén speed12. Here \({V}_{A}=\frac{{B}^{{\rm{0}}}}{\sqrt{4\pi {\rho }^{0}}}\) is called nominal Alfvén speed because it is not the actual speed of the Alfvén wave13,14.

Assume the stratified plasma is bounded by two rigid boundaries y = 0 and y = h. The discrete solutions of Eq. (19) can be found of the form

$${V}_{y}(y)={{\rm{C}}}_{0}\,\sin \,(\frac{m\pi y}{h}){e}^{-\frac{y}{2s}}$$
(20)

where C0 is a constant.

Substituting the Eq. (20) into the Eq. (19), we get a general dispersion relation

$$\omega =\pm \,i{(\frac{g}{s}\frac{{h}^{2}{k}^{2}}{{h}^{2}{k}^{2}+{m}^{2}{\pi }^{2}+{h}^{2}/4{s}^{2}-{{V}_{A}}^{2}/{c}^{2}})}^{\frac{1}{2}}.$$
(21)

The full expression of the linear growth rate of MRTI is

$$\sigma ={(\frac{g}{s}\frac{{h}^{2}{k}^{2}}{{h}^{2}{k}^{2}+{m}^{2}{\pi }^{2}+{h}^{2}/4{s}^{2}-{{V}_{A}}^{2}/{c}^{2}})}^{\frac{1}{2}}.$$
(22)

To investigate the effect of charge accumulation on the linear growth rate of RTI, we nondimensionalize Eq. (21) with the following expressions

$$\sigma =-\,{\rm{i}}\omega \,{\sigma }^{\ast }=\sigma {({\omega }_{{\rm{pe}}})}^{-1}\,{g}^{\ast }=g{({\rm{s}}{\omega }_{pe}^{2})}^{-1}\,{k}^{\ast }=ks,\,{h}^{\ast }=h{(s)}^{-1}.$$

where ωpe is the plasma frequency. We get

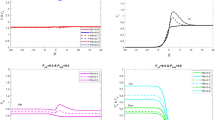
$${\sigma }^{\ast }=({g}^{\ast }\frac{{h}^{\ast 2}{k}^{\ast 2}}{{h}^{\ast 2}{k}^{\ast 2}+{m}^{2}{\pi }^{2}+{h}^{\ast 2}/4-{{V}_{A}}^{2}/{c}^{2}})$$
(23)

Figure 2 shows the dimensionless dispersion relation for the configuration where h* = 1, m = 1, g* = 10, \({V}_{A}^{2}/{{\rm{c}}}^{2}\) = 0, 0.01, 0.1, 0.3, 0.5. Note that the curve representing \({V}_{A}^{2}/{{\rm{c}}}^{2}\) = 0.01 is basically coincided with that of \({V}_{A}^{2}/{{\rm{c}}}^{2}\) = 0. When VA = 0, Eq. (21) represents the dispersion relation for the classical RTI15, and the growth rate is the same as that of the classical RTI. When VA > 0, the growth rate is larger than that of the classical RTI, and increases with the increase of \({V}_{A}^{2}/{{\rm{c}}}^{2}\).

Figure 2
figure 2

The growth rate of RTI (σ*) versus wave number (k*) for different values of \({V}_{A}^{2}/{{\rm{c}}}^{2}\). VA and c are the nominal Alfvén speed and light speed, respectively.

Full size image

In planetary plasma, in general \({V}_{A}\ll c\), the growth rate is basically the same as that of the classical RTI. The contribution of charge accumulation to the growth of MRTI can be neglected. Ignore the displacement current term in Maxwell’s equations when calculate the linear growth rate of MRTI is acceptable. However, the physical description of the MRTI in planetary plasma which attribute the growth of MRTI to charge accumulation is wrong. The physical description of the growth of MRTI is similar to that of neutral fluid16,17. In laboratory plasma, the nominal Alfvén speed is not subject to the constraint \({V}_{A}\ll c\), the growth rate can be much larger than that of the classical RTI. Under such condition, the charge accumulation effect and the displacement current term cannot be ignored. However, the physical description in Fig. 1 which attribute the growth of MRTI to charge accumulation is not accurate, the mechanism for the growth of RTI in neutral fluid works too16,17. Also from Eq. (22) one can see that when the wave number k is very large, the linear growth rate reduce to that of classical RTI, and the effect of charge accumulation can be neglected.

Time scale analysis showed that everything involving charge separation happens on time scales of the inverse plasma frequency, and in such short time scales, the displacement current term cannot be ignored18,19. The MRTI process involves charge accumulation, so the displacement current term should not be ignored during the calculation of the growth rate of MRTI. The displacement current term is neglected because it’s generally small compared to J and curl B term. However, as we can see from Eq. (3) that the \(\frac{\partial {\bf{E}}}{\partial t}\) has the same order of magnitude as J, and the changing electric field have significant effects on the dynamics of the plasma20,21,22. Ignore the displacement current term exclude the effects of electric field on the dynamics of the plasma. It is generally considered that the displacement current, which is closely related to charge separation, must be become negligible under the assumption of quasi-neutrality. However, studies show that when the nominal Alfvén speed is comparable to or larger than the light speed, the displacement current cannot be neglected, regardless of the quasi-neutrality considerations16,23,24, and this is consistent with our result discussed above.