New electrical impedance methods for the in situ measurement of the complex permittivity of anisotropic skeletal muscle using multipolar needles

Abstract

This paper provides a rigorous analysis on the measurement of the permittivity of two-dimensional anisotropic biological tissues such as skeletal muscle using the four-electrode impedance technique. The state-of-the-art technique requires individual electrodes placed at the same depth in contact with the anisotropic material, e.g. using monopolar needles. In this case, the minimum of measurements in different directions needed to estimate the complex permittivity and its anisotropy direction is 3, which translates into 12 monopolar needle insertions (i.e. 3 directions × 4 electrodes in each direction). Here, we extend our previous work and equip the reader with 8 new methods for multipolar needles, where 2 or more electrodes are spaced along the needle’s shaft in contact with the tissue at different depths. Using multipolar needles, the new methods presented reduce the number of needle insertions by a factor of 2 with respect to the available methods. We illustrate the methods with numerical simulations and new experiments on ex vivo ovine skeletal muscle (n = 3). Multi-frequency longitudinal and transverse permittivity data from 30 kHz to 1 MHz is made publicly available in the supplementary material. The methods presented here for multipolar needles bring closer the application of needle electrical impedance to patients with neuromuscular diseases.

Introduction

Electromagnetic fields (EMF) constitute a fundamental physical principle used today for imaging and treating a broad spectrum of conditions including Parkinson disease¹ and brain tumors^2,3. Understanding how the human body interacts with EMF through the complex permittivity property –or simply permittivity–⁴, of biological tissues and fluids is paramount to improve the accuracy of existing techniques as well as to develop new diagnostic tools and therapeutic treatments, for example, for assessment of radiation injury^5,6.

Measuring the permittivity of tissues has been an encompassing effort from many researchers for almost one hundred years^7,8,9,10,11. Unfortunately, to this day, there are still important gaps in knowledge of the in situ values of these properties in many tissues, especially as they relate to anisotropic tissues such as skeletal muscle. Indeed, most of the studies have measured the permittivity of tissues by performing ex situ measurements from biopsy samples. Whereas this may be the simplest approach to measure the permittivity of anisotropic tissues, it is technically challenging to perform and requires the investigator to perform a biopsy procedure. More importantly, ex situ measurements may not be representative of the permittivity measured in situ on alive tissue, as this property is known to change postmortem¹² and with temperature^10,13.

However, measuring in situ the anisotropic nature of permittivity confers an added difficulty in the measurement itself. Importantly, existing in situ methods have important limitations which prevent the user from measuring the anisotropic permittivity accurately^14,15,16. Among the limitations, these methods (i) consider a purely conductive anisotropic material, (ii) require exact knowledge on the anisotropy direction defined by the unknown tissue’s permittivity, and (iii) require aligning perfectly the four-electrode probe in the anisotropy direction.

In our previous work¹⁷, we overcame the existing limitations and developed more sophisticated methods to measure the permittivity using monopolar needles by placing four needles (i.e. four electrodes) in contact with the anisotropic tissue. Among the results, we found that when the direction of the anisotropic permittivity is unknown (i.e. the most general case), then it is necessary to measure the impedance with the four-electrode probe in three or more different directions; otherwise, the error in positioning the four-electrode probe may jeopardize the validity of the calculated permittivity. A consequence that follows from this observation is that when the four-electrode probe is made from monopolar needles, e.g. those used for intramuscular electromyographic recordings, it is necessary to perform at least twelve needle insertions to access inner tissues such as skeletal muscle from the outside. While this may be acceptable in pre-clinical studies, for example to access skeletal muscle tissue through the skin and subcutaneous fat, successful clinical translation of these methods requires the reduction of the number of needle insertions in order to minimize patient discomfort.

The goal of this study is to propel the scientific understanding of anisotropic tissues by enhancing the methods to measure the permittivity of such materials. This article equips the reader with eight new methods, of increasing computational difficulty, to measure the permittivity of anisotropic biological tissues by combining the four-electrode electrical impedance technique with multipolar needles¹⁸. As opposed to the state-of-the-art technique based on monopolar needles¹⁷, the methods presented in this paper, developed for multipolar needles, allow for the reduction in the required number of needle insertions from 12 to 6 this approaching practical application in the clinic.

This a methods paper and it is organized as follows. First, we evaluate the accuracy of the new methods developed by performing numerical simulations and in situ experiments on ex vivo ovine tissue. Next, we discuss the implications of the new methodology. Materials and methods follow thereafter, with particular emphasis on the novel contribution of our work. For completeness and consistency with our previous¹⁷, we briefly review the mathematical background on which all methods presented are based. The first case studied considers multipolar needles with two electrodes changing the angle of measurement. Then, we extend the results to needle devices integrating more than two electrodes while keeping constant the measurement angle. The two previous approaches are then combined to measure the permittivity when the tissues’ anisotropy direction is unknown. The advanced reader can find a rigorous step-by-step derivation of the methods in the supplementary material, otherwise, the information necessary to use each method is contained in the main document.

Results

Simulation

Benchmark results: simulation example of methods H1, H2 and H3

The methods developed for multipolar needles are simulated following the same rationale as our previous work to facilitate comparison with the state-of-the-art based on monopolar needles¹⁷. We used MATLAB software (The Mathworks, Inc., Natick, MA) to generate M = 10 noisy apparent resistivity and apparent reactivity values giving a signal-to-noise ratio (SNR) of 30 dB. Further, the needle-distance aspect ratio was considered p = 8.6. The true anisotropic permittivity of muscle at 10 kHz was taken from a database¹⁹, namely the transverse resistivity ρ_T = 2.93 Ω m and the transverse relative permittivity ε_r,T = 2.59 ⋅ 10⁴ (dimensionless), denoted by the subscript T. We compute the longitudinal (denoted by the subscript L) permittivity from the transverse permittivity values using an anisotropy ratio α² = 0.5, i.e. ρ_L = 1.47 Ω m and ε_r,L = 1.30 ⋅ 10⁴ (dimensionless). We represent the apparent resistivity and apparent reactivity in (3) in polar plots to show its angular dependence.

Figure 1 shows a single-frequency comparison of methods H1 to H3 measuring the anisotropic permittivity of skeletal muscle tissue. The angles considered in method H1 are the longitudinal and transverse directions defined by the anisotropy in the material, i.e. ϕ_L = π/2 and ϕ_T = 0 respectively (Fig. 1A). Method H1 is extended to method H2 by considering two arbitrary angles θ₁ = π/6 and θ₂ = π/3 (Fig. 1B). The number of angles measured is then extended to eight angles in method H3, i.e. ${\theta }_{\mathrm{\{1,}\cdots \mathrm{,8\}}}$ from 0 to 5π/6 (Fig. 1C).

Figure 1

Numerical simulation results using methods H1 (A), H2 (B), and H3 (C). The estimated impedivity in longitudinal (L) and transverse (T) directions ${\hat{\kappa }}_{\{L,{\rm{T}}\}}$ (shown in crosses) were calculated from M = 10 averaged apparent impedivity ${\hat{\kappa }}_{{\rm{a}}}({\theta }_{d})$ measurements (shown in circles), with d = 1, …, D the measurement angles and inter-electrodes’ distance p = 8.6. Method H1 (D = 2): ${\hat{\rho }}_{{\rm{L}}}=1.56$ Ω m, ${\hat{\rho }}_{{\rm{T}}}=2.71$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.13$ Ω m; Method H2 (D = 2): ${\hat{\rho }}_{{\rm{L}}}=1.57$ Ω m and ${\hat{\rho }}_{{\rm{T}}}=2.71$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.12$ Ω m; Method H3 (D = 8): ${\hat{\rho }}_{{\rm{L}}}=1.54$ Ω m, ${\hat{\rho }}_{{\rm{T}}}=2.76$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.13$ Ω m. The true longitudinal and transverse resistivity (i) and reactivity (ii) are plotted in dash-dot and dashed circumferences, ρ_L = 1.46 Ω m, ρ_T = 2.93 Ω m, τ_L = −0.06 Ω m and τ_T = −0.12 Ω m, respectively. The reactivity is shown −τ as a convention. The units of impedivity are Ω m.

The estimated (denoted byˆ) longitudinal and transverse resistivity and reactivity ${\hat{\rho }}_{\{{\rm{L}},{\rm{T}}\}}$ and ${\hat{\tau }}_{\{{\rm{L}},{\rm{T}}\}}$ are represented by crosses (×) in the y-axis (ϕ_L) and x-axis (ϕ_T), respectively. To help the reader interpret the data, the estimated values represented by the crosses should appear as close as possible to the true values, i.e. ρ_{L,T} and τ_{L,T}, the latter represented by dash-dot and dashed circumferences where intersect the longitudinal ϕ_L and transverse ϕ_T axes, respectively.

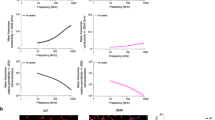
Note the accuracy of the aforementioned methods depends on both the SNR and M. To study the dependence of the precision of the methods based on these two parameters, we plot in Fig. 2A and B the accuracy of the resistivity anisotropy ratio while varying the SNR and the number of measurements M. The most accurate method is H3, then H1, and finally H2.

Figure 2

Comparison between methods H1 (solid grey line), H2 (dashed black line), and H3 (solid black line) estimating the resistivity anisotropy ratio ${\hat{\alpha }}^{2}$ while changing the signal-to-noise ratio (SNR) and keeping the number of measurements constant at M = 10 (A); and then while changing the number of measurements performed and keeping constant the SNR = 40 dB (B). Rates of decline of the relative error values between the estimated ${\hat{\alpha }}^{2}$ and true α² resistivity anisotropy ratio value are graphically shown, calculated with a linear regression.

Benchmark results: simulation example of methods K2 and K3

To evaluate the accuracy of the approximation, for example in (10), we calculate the relative error in ${\hat{\alpha }}^{2}$. The relative error in ${\hat{\alpha }}^{2}$ is 11.5% and 17.0% for methods K2 and K3. Note the accuracy of methods K2 and K3 will largely depend on the measurement angles θ_d. When θ_d is close to 0 or π/2, the methods will provide more accurate estimates and vice versa (see Fig. 3). The estimated longitudinal and transverse resistivity and reactivity ${\hat{\rho }}_{\{{\rm{L}},{\rm{T}}\}}$ and ${\hat{\tau }}_{\{{\rm{L}},{\rm{T}}\}}$ are represented are shown in Fig. 4. Moreover, Fig. 5 shows that, unlike method K3, method K2 barely improves when the SNR or the number of measures increases.

Figure 3

Apparent resistivity ρ_a = real(κ_a) from (3) (solid black line) and the corresponding approximations ${\hat{\rho }}_{{\rm{a}}\mathrm{,1}}={\rm{real}}({\hat{\kappa }}_{{\rm{a}}\mathrm{,1}})$ in (8) (dashed grey line), ${\hat{\rho }}_{{\rm{a}}\mathrm{,2}}={\rm{real}}({\hat{\kappa }}_{{\rm{a}}\mathrm{,2}})$ in (9) (dotted grey line), ${\hat{\rho }}_{{\rm{a}}\mathrm{,3}}={\rm{real}}({\hat{\kappa }}_{{\rm{a}}\mathrm{,3}})$ in (10) (solid grey line). Simulation settings: aspect ratio p = 8.6, anisotropy ratio α² = 0.5, measured frequency f = 10 kHz, transverse resistivity ρ_T = 2.93 Ω m.

Figure 4

Numerical simulation results using methods K2 (A) and K3 (B). The estimated impedivity in longitudinal (L) and transverse (T) directions ${\hat{\kappa }}_{\{L,{\rm{T}}\}}$ (shown in crosses) were calculated from M = 10 averaged apparent impedivity ${\hat{\kappa }}_{{\rm{a}}}({\theta }_{d})$ measurements (shown in circles), with d = 1, …, D the measurement angles and interelectrodes’ distance p = 8.6. Method K2 (D = 2): ${\hat{\rho }}_{{\rm{L}}}=1.73$ Ω m, ${\hat{\rho }}_{{\rm{T}}}=2.47$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.07$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.10$ Ω m; Method K3 (D = 8): ${\hat{\rho }}_{{\rm{L}}}=1.49$ Ω m, ${\hat{\rho }}_{{\rm{T}}}=2.89$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.13$ Ω m. The true longitudinal and transverse resistivity (i) and reactivity (ii) are plotted in in dash-dot and dashed circumferences, ρ_L = 1.46 Ω m, ρ_T = 2.93 Ω m, τ_L = −0.06 Ω m and τ_T = −0.12 Ω m, respectively. The reactivity is shown −τ as a convention. The units of impedivity are Ω m.

Figure 5

Comparison between methods K2 (dashed black line) and K3 (solid black line) estimating the resistivity anisotropy ratio ${\hat{\alpha }}^{2}$ while changing the signal-to-noise ratio (SNR) and keeping the number of measurements constant at M = 10 (A); and then while changing the number of measurements performed and keeping constant the SNR = 40 dB (B). Rates of decline of the relative error values between the estimated ${\hat{\alpha }}^{2}$ and true α² resistivity anisotropy ratio value are graphically shown, calculated with a linear regression.

Benchmark results: simulation example of methods B1 and B2

Figure 6 shows the results of methods B1 and B2 measuring apparent impedivity data with N = 2 (p₁ = 20, p₂ = 8.6) and N = 5 (p₁ = 20, p₂ = 8.6, p₃ = 5.5, p₄ = 4.0, p₅ = 3.2) inter-electrodes’ distances and one measurement angle, respectively. To avoid confusion, we show the mean apparent resistivity and the mean aparent reactivity values (in circles) for each inter-electrodes’ distances slightly displaced on the same direction; otherwise, the circles would be superimposed one on top of the other, appearing with the naked eye as if there was one data point only. Figure 7 shows method B2 is more accurate than method B1.

Figure 6

Numerical simulation results using methods B1 (A) and B2 (B). The estimated impedivity in longitudinal (L) and transverse (T) directions ${\hat{\kappa }}_{\{L,{\rm{T}}\}}$ (shown in crosses) were calculated from M = 10 averaged apparent impedivity ${\hat{\kappa }}_{{\rm{a}}}({p}_{n})$ measurements (shown in circles), with n = 1, …, N the number of inter-electrodes’ distances and θ = π/4 the measurement angle. Method B1 (N = 2): ${\hat{\rho }}_{{\rm{L}}}=1.57$ Ω m, ${\hat{\rho }}_{{\rm{T}}}=2.73$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.12$ Ω m; Method B2 (N = 5): ${\hat{\rho }}_{{\rm{L}}}=1.45$ Ω m and ${\hat{\rho }}_{{\rm{T}}}=2.94$ Ω m, ${\hat{\tau }}_{{\rm{L}}}=-\,0.06$ Ω m, ${\hat{\tau }}_{{\rm{T}}}=-\,0.13$ Ω m. The true longitudinal and transverse resistivity (i) and reactivity (ii) are plotted in dash-dot and dashed circumferences, ρ_L = 1.46 Ω m, ρ_T = 2.93 Ω m, τ_L = −0.06 Ω m and τ_T = −0.12 Ω m, respectively. The reactivity is shown −τ as a convention. The units of impedivity are Ω m.

Figure 7

Comparison between methods B1 (dashed black line) and B2 (solid black line) estimating the resistivity anisotropy ratio ${\hat{\alpha }}^{2}$ while changing the signal-to-noise ratio (SNR) and keeping the number of measurements constant at M = 10 (A); and then while changing the number of measurements performed and keeping constant the SNR = 40 dB (B). Rates of decline of the relative error values between the estimated ${\hat{\alpha }}^{2}$ and true α² resistivity anisotropy ratio value are graphically shown, calculated with a linear regression.

Experiment

Data measured in situ were estimated using method S1, the only method capable of measuring the permittivity regardless of the anisotropy direction. Data shown in Figs 8 and 9 are not intended for analytical purposes. Rather the goal is to show experimental feasibility and proof-of-concept measuring the permittivity of anisotropic muscle tissue in situ combining the method developed in this work with multipolar needles.

Figure 8

Estimated conductivity in longitudinal (blue) and transverse (red) direction. In situ mean ± standard deviation (M = 3 measurements).

Figure 9

Estimated relative permittivity in longitudinal (blue) and transverse (red) direction. In situ mean ± standard deviation (M = 3 measurements).

Discussion

Numerous studies published over the last decades have reported the permittivity of biological fluids and tissues^20,21,22. Having accurate methods to measure this physical property is fundamental to advance the development and research of medical technology²³.

Despite the importance, even today there are still major gaps in the knowledge of the frequency-dependence of the permittivity of certain tissues. A review of the literature shows that actually only a few studies have been made on human skeletal muscle tissue^24,25; in a few others, the anisotropic permittivity of muscle was measured in animals^26,27,28. However, we are unaware of the existence of any study that has measured in vivo the permittivity of healthy or diseased muscle in patients.

Much of the reason for the paucity of studies measuring tissues’ anisotropic permittivity are the limitations of the methods associated with the existing measurement techniques. In the case of using the four-electrode impedance technique, one main limitation of the method reported by Rush is that prior knowledge is required concerning the direction of the tissue’s anisotropy¹⁴. The solution proposed by Rush has been widely used because of its simplicity; however, it is well-known it has limitations restricting its practical use²⁹. For example, in animal experimentation, the direction of anisotropy can be approximated in vivo by visual inspection removing the skin and subcutaneous fat overlying the muscle but this is not possible in patients³⁰. The second main limitation is that if the anisotropy direction is unknown (e.g. measuring muscle from outside by inserting the a four-electrode probe through the skin and subcutaneous fat tissues), we have shown that the minimum number of needle insertions needed to measure anisotropic permittivity is twelve, i.e. method C4 in Table 1¹⁷. This approach is valuable in pre-clinical studies; however, its clinical translation is questionable. Changing the experimental measurement from monopolar to multipolar needles and developing new S1 method, our study shows that it is possible to measure anisotropic permittivity while reducing the needle insertions required from twelve to six.

Table 1 Comparison of electrical impedance methods for the in situ measurement of anisotropic permittivity.

Since we are interested in muscle permittivity, the methods presented were developed for the measurement of materials with different anisotropies in two dimensions only. Developing methods accounting for the most general case of anisotropy in three dimensions is beyond the scope of the work presented. As for the dispersion in the experimental data, it can be attributed to several factors including the small sample size, biological variability, and the time elapsed between the death of the animals and the measurements. Still, the results are consistent with data available in the literature. For example, in canine skeletal muscle, the transverse conductivity has been reported from 0.04 to 0.10 S m^−1 26,31. There are other practical limitations affecting our methods, but these also apply to any other in situ method using needles^32,33. For example, a fluid channel surrounding the electrodes will influence the data offering a less resistive path for the electrical current to flow. If the needles are very closely approximated to each other, the distribution of electrical current and thus the electric potential will be affected. Depending on the tissue being studied, if the electrodes are far apart from each other, the anisotropy direction may change. All these issues are possible sources of errors and they should be considered when performing experimental measurements.

Ultimately, we aim to measure muscles’ anisotropic permittivity in vivo to track disease progression and evaluate treatment effect in patients with neuromuscular diseases (NMD)^34,35. In NMD, the pathophysiology of the disease alters the structure and composition of muscle tissue, which changes the permittivity of muscle and its anisotropy direction. For example, Duchenne muscular dystrophy is characterized by the loss of muscle fibers and their progressive substitution by fat and fibrous tissue. Improving our ability to measure with accuracy muscle permittivity can yield insight into developing new strategies for newer and more accurate diagnostic tools and treatments. This work is a step towards this direction and warrants further research to further reduce the number of needle insertions required to measure muscle permittivity in vivo.

Materials

Animals

Measurements were performed at the Animal Research Facility of Beth Israel Deaconess Medical Center in Boston, MA. This study did not require Institutional Animal Care and Use Committee approval because the animals were used for another experiment and measured here postmortem. We followed the same experimental procedure as our previous study¹⁷. In situ measurements on healthy skeletal muscle tissue from a freshly killed sheep (n = 3) were conducted at room temperature (25 °C) immediately after the animals were euthanized and completed within 1 hour postmortem. The skin and subcutaneous fat tissues were reflected back and the medius gluteus muscle exposed. Then, the multipolar needles were inserted into the muscle.

Impedance measuring device

Ovine muscle impedance was measured using a commercial impedance analyzer (SFB7. Impedimed, Inc., Brisbane, Australia) using stepped-sine current excitation between 30.4 kHz and 1 MHz (155 frequencies total). For the positioning of multipolar needles we used a custom made matrix device¹⁷.

Matrix device and multipolar needle

The custom made printed circuit board (PCB) was already described in¹⁷ (Fig. 10A). Briefly, the PCB was positioned in contact with the surface of the muscle without considering any pre-specified direction. Then, two multipolar needles described in³⁶ were inserted into the muscle tissue at a constant depth of 20 mm at predefined positions (Fig. 10B). Multi-frequency impedance data (number of measurements per angle M = 3) were then collected sequentially changing the electrodes’ configuration as detailed in Table 2. The aspect factors resulting from the separation between the needles g = 30 mm and the inter-electrodes’ distance h₁ = 1.5 mm, h₂ = 3.5 mm, and h₃ = 5 mm, were p₁ = 20, p₂ = 8.6, p₃ = 6. The reader is referred to Supplementary information, Part E for further information regarding the manufacturing of the needles.

Figure 10

Printed circuit board (A)¹⁷ and multipolar needle (B)³⁶ used for performing in situ measurements of ovine ex vivo muscle. The needles integrate a total of five electrodes, four electrodes arranged along the shaft of the needle, and a fifth, at the tip of the needle. Electrode 5 was not used in this study. The reader is referred to Table 2 for the measurement details.

Table 2 Experimental configuration employed for in situ experiments based on method S1.

Data analysis

Multi-frequency muscle impedance data were analyzed using method S1 using MATLAB. We calibrated apparent muscle impedance measured (resistance and reactance in Ω) into impedivity (resistivity and reactivity in Ω m) by performing impedance measurements in saline solution. We used the same experimental setup as in the in situ measurements. Calibration measurements were taken at room temperature immediately after immersing the needle electrode matrix into saline solution.

Methods

Terminology and definitions

The electric voltage $V\in {\mathbb{C}}$ (V) created by a current point-electrode in a (semi-)infinite, homogenous anisotropic tissue with anisotropicity in the y-axis and relative permittivity ${\varepsilon }_{r}\in {{\mathbb{R}}}_{ > 0}$ (dimensionless) is

$$V=\frac{{\kappa }_{\alpha }I}{K|{r}_{\alpha }|},$$

(1)

where I (A) is the applied current; ${\kappa }_{\alpha }\,:\,=\sqrt{{\kappa }_{{\rm{T}}}{\kappa }_{{\rm{L}}}}$ with ${\kappa }_{\{{\rm{L}},{\rm{T}}\}}={\rho }_{\{{\rm{L}},{\rm{T}}\}}+i{\tau }_{\{{\rm{L}},{\rm{T}}\}}$ (Ω m) the impedivity in longitudinal (L) and transverse (T) directions with ρ and τ the resistivity and the reactivity (Ω m), respectively; $i\,:\,=\sqrt{-1}$ is the imaginary unit (dimensionless); K = 2π, 4π (dimensionless) is a constant factor for semi-infinite and infinite domains, respectively; r_α = (x, αy, z) is the apparent position; the operator |·| is the L₂ norm; and α²: = ρ_L/ρ_T = τ_L/τ_T (dimensionless) is the equal anisotropy ratio for the monodomain model. In the specific case in which the anisotropic tissues are considered purely resistive as in¹⁴ (i.e. ε_r = 0 and so τ = 0), (1) still holds with $V\in {\mathbb{R}}$ and where κ_α is replaced by the apparent resistivity ${\rho }_{\alpha }\,:\,=\sqrt{{\rho }_{{\rm{T}}}{\rho }_{{\rm{L}}}}$ (Ω m).

Rush’s first work and our recent study¹⁷ are similar in that the methods developed to measure the complex permittivity ε: = ε′ + iε″ (dimensionless, henceforth referred simply as permittivity) of anisotropic tissues are based on (1) considering the z-component of the four-electrodes’ probe apparent position r_α is zero. In other words, the existing methods require the placement of the four-electrodes on the xy-plane (see Fig. 11). In doing so, the apparent impedivity (Ω m) measured using the principle of superposition in polar coordinates and the four-electrode technique reduces to

$${\kappa }_{{\rm{a}}}({\theta }_{d})=\frac{{\kappa }_{\alpha }}{\sqrt{{\cos }^{2}{\theta }_{d}+{\alpha }^{2}{\sin }^{2}{\theta }_{d}}}.$$

(2)

Figure 11

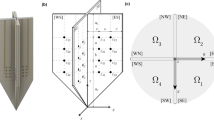
(A) Schematic showing the in situ measurement of anisotropic permittivity in D = 2 angles using monopolar needles^14,17. Current and voltage electrodes are at the same depth, shown in red and blue color, respectively. (B) Schematic of the d-th angle measured in the xy-plane (z = 0). The measurement angle θ_d is defined with respect to the muscle fibers’ transverse (T) {x, z} direction ϕ_T (i.e. ϕ_T = θ when θ = 0) and ϕ_L is the longitudinal y direction. Electrode configuration: ${ {\mathcal E} }_{I}^{2d-1}$, source current electrode; ${ {\mathcal E} }_{V}^{2d-1}$, high potential electrode; ${ {\mathcal E} }_{V}^{2d}$, low potential electrode; ${ {\mathcal E} }_{I}^{2d}$, sink current electrode; where $d=\mathrm{1,}\,\mathrm{2,}\,\cdots ,\,D$ and D is the number of different angles measured from 0 to π with θ_i + θ_j ≠ π for $i,j\in \mathrm{\{1,}\,\mathrm{2,}\,\cdots ,\,D\}$ and i ≠ j.

Then, from (2), the only possible way of obtaining anisotropy information on ε is by measuring the apparent impedivity κ_a in two or more different directions θ and computing α and κ_α, where θ is defined as the measuring angle (in radians) with respect to the transverse direction ϕ_T determined by the tissues’ anisotropy.

In this paper, we extend our previous study by developing new methods that allow us to place the electrodes for measuring impedance at varying depths in the tissues by changing the z coordinate. In the same way as before, the ultimate goal of the methods is to estimate κ_{L,T}; however, for notational convenience, the methods presented below are based on estimating α² and κ_α instead. In the end, the reader can compute κ_{L,T} by simply using the following relationships

$${\kappa }_{{\rm{T}}}=\frac{{\kappa }_{\alpha }}{\alpha }\,{\rm{and}}\,{\kappa }_{{\rm{L}}}=\alpha {\kappa }_{\alpha }$$

(or its resistive analogue when considering ε_r = 0, i.e. replacing κ by ρ) and subsequently the permittivity

$${\varepsilon }_{\{{\rm{L}},{\rm{T}}\}}=\frac{1}{i\omega {\varepsilon }_{0}{\kappa }_{\{{\rm{L}},{\rm{T}}\}}}={\varepsilon }_{r,\{{\rm{L}},{\rm{T}}\}}-i\frac{{\sigma }_{\{{\rm{L}},{\rm{T}}\}}}{\omega {\varepsilon }_{0}},$$

with ω = 2πf (rad s⁻¹) the (angular) frequency f (Hz) measured, ε₀ (F m⁻¹) the vacuum permittivity, ε_r the relative permittivity (dimensionless), and σ the conductivity (S m⁻¹).

Henceforth, the naming convention of the methods presented is H, K, B, and S to distinguish from our previous work¹⁷.

One inter-electrodes’ distance within the same needle and multiple measurement angles

Let’s start considering the measurement setting shown in Fig. 12(A). According to Fig. 12(B), the apparent impedivity κ_a based on (1) is (see Theorem 1 in Supplementary information, Part A)

$${\kappa }_{{\rm{a}}}({\theta }_{d})={\kappa }_{\alpha }(1-\frac{1}{p\sqrt{{\cos }^{2}{\theta }_{d}+{\alpha }^{2}{\sin }^{2}{\theta }_{d}}}),$$

(3)

where $p\,:\,=g/h\in {{\mathbb{R}}}_{ > 0}$ (dimensionless) is the aspect ratio computed from h (m) the distance between electrodes in the z axis and g (m) the distance between electrodes in the same xy plane.

Figure 12

(A) Schematic showing the in situ measurement of anisotropic permittivity in D = 2 angles using multipolar needles. N.b. compared to Fig. 11, the pairs of current and voltage electrodes have different coordinates in the z-direction (in red and blue color, respectively). (B) Schematic of the d-th angle measured in the xy-plane (z = 0). The measurement angle θ_d is defined with respect to the muscle fibers’ transverse (T) {x, z} direction ϕ_T (i.e. ϕ_T = θ when θ = 0) and ϕ_L is the longitudinal y direction. Electrode configuration: ${ {\mathcal E} }_{I}^{2d-1}$, source current electrode; ${ {\mathcal E} }_{V}^{2d-1}$, high potential electrode; ${ {\mathcal E} }_{V}^{2d}$, low potential electrode; ${ {\mathcal E} }_{I}^{2d}$, sink current electrode; where $d=\mathrm{1,}\,\mathrm{2,}\,\cdots ,\,D$ is the number of different angles measured from 0 to π.

Below we provide three methods, from less to more general, to estimate the apparent impedivity ${\hat{\kappa }}_{\alpha }$ and the anisotropy ratio ${\hat{\alpha }}^{2}$ at a given measured frequency. First, the methods H1, H2 and H3 are developed based on (3). We then develop methods K2 and K3 after approximating (3). In both cases, the frequency dependence of the anisotropic impedivity can be computed iterating the methods presented at each particular frequency measured.

For consistency, we use the same nomenclature convention as in our previous work¹⁷. Noisy apparent impedivity data is denoted by the m superscript notation, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{d})={\rho }_{{\rm{a}}}^{[m]}({\theta }_{d})+i{\tau }_{{\rm{a}}}^{[m]}({\theta }_{d})$. The measurement index is m and $M\in {\mathbb{N}}$ is the total number of measurements considered. Multiple measurements are performed sequentially for each measurement angle θ_d angles, where $d=\mathrm{1,}\cdots ,D$ and $D\in {{\mathbb{N}}}_{\ge 2}$ is the total number of angles measured. The averaged values within the experiment index m are denoted with the ˆ notation, i.e. ${\hat{\kappa }}_{{\rm{a}}}({\theta }_{d})\,:\,={\hat{\rho }}_{{\rm{a}}}({\theta }_{d})+i{\hat{\tau }}_{{\rm{a}}}({\theta }_{d})$.

Method H1: The apparent impedivity is measured in $D=2$ angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{1})$ and ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{2})$, with ${\theta }_{1}\perp {\theta }_{2}$ and ${\theta }_{\{1,2\}}\in [0,\pi )$

Placing the electrodes in the anisotropic directions defined by the properties of the material is the simplest approach to estimate the anisotropy ratio ${\hat{\alpha }}^{2}$ and the geometric mean impedivity κ_α from (3) (see Theorem 2 in Supplementary information, Part B). Then,

$$\{\begin{array}{lll}{\hat{\kappa }}_{\alpha } & := & p{\hat{\kappa }}_{{\rm{a}}}\mathrm{(0)(}p-{\mathrm{1)}}^{-1}\\ {\hat{\alpha }}^{2} & := & {\hat{\rho }}_{{\rm{a}}}^{2}\mathrm{(0)(}p({\hat{\rho }}_{{\rm{a}}}\mathrm{(0)}-{\hat{\rho }}_{{\rm{a}}}(\pi \mathrm{/2))}+{\hat{\rho }}_{{\rm{a}}}(\pi {\mathrm{/2))}}^{-2}\\ & {\rm{or}} & {\hat{\tau }}_{{\rm{a}}}^{2}\mathrm{(0)(}p({\hat{\tau }}_{{\rm{a}}}\mathrm{(0)}-{\hat{\tau }}_{{\rm{a}}}(\pi \mathrm{/2))}+{\hat{\tau }}_{{\rm{a}}}(\pi {\mathrm{/2))}}^{-2}.\end{array}$$

(4)

The readers’ choice of using the apparent resistivity or the apparent reactivity to calculate ${\hat{\alpha }}^{2}$ in (4) should be based on the measurement noise. Note that Assumption 2 guarantees that the potential difference ${\rm{\Delta }}V\,:\,=V({ {\mathcal E} }_{V}^{2d})-V({ {\mathcal E} }_{V}^{2d-1})\ne 0$, where d ∈ {1, 2} corresponds to the measurement angle θ_d in the transverse direction ϕ_T determined by the tissues’ anisotropy. In other words, the apparent positions of the voltage measuring electrodes ${r}_{\alpha }({ {\mathcal E} }_{V}^{2d})$ and ${r}_{\alpha }({ {\mathcal E} }_{V}^{2d-1})$ are not on the same equipotential surface.

Method H2: The apparent impedivity is measured in $D=2$ angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{1})$ and ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{2})$, and θd ∈ (0, π)

Method H1 can be generalized for any pair of angles. In this case, the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ can be estimated from the apparent impedivity values found after solving a 4-th degree polynomial ${P}_{4}({\hat{\kappa }}_{\alpha })\,:\,={\sum }_{n=0}^{4}{\lambda }_{n}{\hat{\kappa }}_{\alpha }^{n}$, where the coefficients are (see Theorem 3 in Supplementary information, Part B)

$$\begin{array}{lll}{\lambda }_{4} & := & {a}_{11}{a}_{22}-{a}_{12}{a}_{21},\\ {\lambda }_{3} & := & {a}_{11}{b}_{21}-{a}_{12}{a}_{23}+{a}_{13}{a}_{22}-{b}_{11}{a}_{21},\\ {\lambda }_{2} & := & -{a}_{11}{c}_{2}-{a}_{12}{b}_{22}+{a}_{13}{b}_{21}-{b}_{11}{a}_{23}+{b}_{12}{a}_{22}+{c}_{1}{a}_{21},\\ {\lambda }_{1} & := & -{a}_{13}{c}_{2}-{b}_{11}{b}_{22}+{b}_{12}{b}_{21}+{c}_{1}{a}_{23},\\ {\lambda }_{0} & := & {c}_{1}{b}_{22}-{b}_{12}{c}_{2},\end{array}$$

and

$$\begin{array}{c}{a}_{d1}\,:\,={p}^{2}{\sin }^{2}{\theta }_{d},\,{a}_{d2}\,:\,={p}^{2}{\cos }^{2}{\theta }_{d}-1,\,{a}_{d3}\,:\,=-\,2{p}^{2}{\sin }^{2}{\theta }_{d}{\hat{\kappa }}_{a}({\theta }_{d}),\\ {b}_{d1}\,:\,=-\,2{p}^{2}{\cos }^{2}{\theta }_{d}{\hat{\kappa }}_{a}({\theta }_{d}),\,{b}_{d2}\,:\,={p}^{2}{\sin }^{2}{\theta }_{d}{\hat{\kappa }}_{a}^{2}({\theta }_{d}),\,{c}_{d}\,:\,=-\,{p}^{2}{\cos }^{2}{\theta }_{d}{\hat{\kappa }}_{a}^{2}({\theta }_{d})\end{array}$$

(5)

for d = 1, 2. The analytic solution ${\hat{\kappa }}_{\alpha }$ to a 4-th degree equation exists. Then, we can estimate the anisotropy ratio ${\hat{\alpha }}^{2}$ as follows

$${\hat{\alpha }}^{2}\,:\,=-\,\frac{{a}_{22}{\hat{\kappa }}_{\alpha }^{2}+{b}_{21}{\hat{\kappa }}_{\alpha }-{c}_{2}}{{a}_{21}{\hat{\kappa }}_{\alpha }^{2}+{a}_{23}{\hat{\kappa }}_{\alpha }+{b}_{22}}.$$

(6)

Care should be taken when using the method above with p < 1. Note there exist some combination of θ_d and α² that makes κ_a = 0 in (3), and α² is unknown.

Method H3: The apparent impedivity is measured in D ≥ 2 angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{d})$, and ${\theta }_{d}\in [\mathrm{0,}\,\pi )$

In general, for any number of measured angles D ≥ 2, the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ can be estimated by finding the roots of an 11-th degree polynomial ${P}_{11}({\hat{\kappa }}_{\alpha }):={\sum }_{n=0}^{11}{\mu }_{n}{\hat{\kappa }}_{\alpha }^{n}$. The coefficients μ_n do not have a compact expression and are therefore detailed in Theorem 4 in Supplementary information, Part B. Then, we can estimate anisotropy ratio ${\hat{\alpha }}^{2}$ as follows

$${\hat{\alpha }}^{2}\,:\,=-\,\frac{{{\bf{a}}}_{1}^{\top }{{\bf{a}}}_{2}{\hat{\kappa }}_{\alpha }^{4}+({{\bf{a}}}_{2}^{\top }{{\bf{a}}}_{3}+{{\bf{a}}}_{1}^{\top }{{\bf{b}}}_{1}){\hat{\kappa }}_{\alpha }^{3}+({{\bf{a}}}_{2}^{\top }{{\bf{b}}}_{2}+{{\bf{a}}}_{3}^{\top }{{\bf{b}}}_{1}-{{\bf{a}}}_{1}^{\top }{\bf{c}}){\hat{\kappa }}_{\alpha }^{2}+({{\bf{b}}}_{2}^{\top }{{\bf{b}}}_{1}-{{\bf{a}}}_{3}^{\top }{\bf{c}}){\hat{\kappa }}_{\alpha }-{{\bf{b}}}_{2}^{\top }{\bf{c}}}{{{\bf{a}}}_{1}^{\top }{{\bf{a}}}_{1}{\hat{\kappa }}_{\alpha }^{4}+2{{\bf{a}}}_{1}^{\top }{{\bf{a}}}_{3}{\hat{\kappa }}_{\alpha }^{3}+({{\bf{a}}}_{3}^{\top }{{\bf{a}}}_{3}+2{{\bf{a}}}_{1}^{\top }{{\bf{b}}}_{2}){\hat{\kappa }}_{\alpha }^{2}+2{{\bf{a}}}_{3}^{\top }{{\bf{b}}}_{2}{\hat{\kappa }}_{\alpha }+{{\bf{b}}}_{2}^{\top }{{\bf{b}}}_{2}}$$

(7)

where ${{\bf{a}}}_{1}\,:\,={[{a}_{11},{a}_{21},\cdots ,{a}_{D1}]}^{\top }$, ${{\bf{a}}}_{2}\,:\,={[{a}_{12},{a}_{22},\cdots ,{a}_{D2}]}^{\top }$, ${{\bf{a}}}_{3}\,:\,={[{a}_{13},{a}_{23},\cdots ,{a}_{D3}]}^{\top }$, ${{\bf{b}}}_{1}\,:\,={[{b}_{11},{b}_{21},\cdots ,{b}_{D1}]}^{\top }$, ${{\bf{b}}}_{2}\,:\,={[{b}_{12},{b}_{22},\cdots ,{b}_{D2}]}^{\top }$, ${\bf{c}}\,:\,={[{c}_{1},{c}_{2},\cdots ,{c}_{D}]}^{\top }$, where a_d1, a_d2, a_d3, b_d1, b_d2, c_d are defined in (5) for $d=\mathrm{\{1,}\,\mathrm{2,}\,\cdots ,\,D\}$, and where $\top$ denotes the transpose operator.

Approximation

Applying methods H2 and H3 require finding the roots of a 4-th and 11-th degree polynomial, respectively. Therefore, there can be one or more physically meaningful solutions ${\hat{\kappa }}_{\alpha }$ within the 4 and 11 respective complex solutions. If so, choosing the right ${\hat{\kappa }}_{\alpha }$ may be challenging or impossible without a priori information. To decrease the order of the polynomial and therefore the number of possible solutions, we approximate square root in (3) as follows

$$\sqrt{{\cos }^{2}\theta +{\alpha }^{2}{\sin }^{2}\theta }\approx \phi (\theta )+\alpha \mathrm{(1}-\phi (\theta )),$$

where φ(θ) is a user-defined suitable function that does not depend on α, for example

$${\hat{\kappa }}_{{\rm{a}},1}\,:\,={\kappa }_{\alpha }(1-\frac{1}{p\mathrm{((1}-\alpha ){\cos }^{2}\theta +\alpha )})\,{\rm{with}}\,\phi (\theta )={\cos }^{2}\theta ,$$

(8)

$${\hat{\kappa }}_{{\rm{a}},2}\,:={\kappa }_{\alpha }(1-\frac{1}{p((1-\alpha )|\cos \theta |+\alpha )})\,{\rm{w}}{\rm{i}}{\rm{t}}{\rm{h}}\,\phi (\theta )=|\cos \theta |,$$

(9)

$${\hat{\kappa }}_{{\rm{a}},3}\,:={\kappa }_{\alpha }(1-\frac{1}{p((1-\alpha )({\cos }^{2}\theta +|\cos \theta |)/2+\alpha )})\,{\rm{w}}{\rm{i}}{\rm{t}}{\rm{h}}\,\phi (\theta )=\frac{1}{2}({\cos }^{2}\theta +|\cos \theta |).$$

(10)

and ${\hat{\kappa }}_{{\rm{a}},j}$ for j = 1, 2, 3 are suitable approximations (see Fig. 3) of the apparent impedivity in (3) (denoted by the notation~). The new approximated methods H2 and H3 based on (8–10) are named K2 and K3 (note method H1 does not require to be approximated since the estimation of ${\hat{\kappa }}_{\alpha }$ is unique).

Method K2: The apparent impedivity is measured in $D=2$ angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{1})$ and ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{2})$

The anisotropy ratio ${\hat{\alpha }}^{2}$ can be estimated as from the apparent impedivity values measured in any combination of two angles (see Theorem 5 in Supplementary information, Part B) as follows

$${\hat{\alpha }}^{2}\,:\,={(\frac{{\mu }_{1}^{2}-2{\mu }_{0}{\mu }_{2}\mp {\mu }_{1}\sqrt{{\mu }_{1}^{2}-4{\mu }_{2}{\mu }_{0}}}{2{\mu }_{2}^{2}})}^{2}\,{\rm{or}}\,{(\frac{{\nu }_{1}^{2}-2{\nu }_{0}{\nu }_{2}\mp {\nu }_{1}\sqrt{{\nu }_{1}^{2}-4{\nu }_{2}{\nu }_{0}}}{2{\nu }_{2}^{2}})}^{2},$$

(11)

where μ₀, μ₁, μ₂, ν₀, ν₁, ν₂ are defined as

$$\{\begin{array}{lll}{\mu }_{2} & := & p\mathrm{(1}-\phi ({\theta }_{1}\mathrm{))(1}-\phi ({\theta }_{2}))({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2}))\\ {\mu }_{1} & := & p({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2}))(\phi ({\theta }_{1})+\phi ({\theta }_{2})-2\phi ({\theta }_{1})\phi ({\theta }_{2}))\\ & & -({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2}))+({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})\phi ({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2})\phi ({\theta }_{2}))\\ {\mu }_{0} & := & p\phi ({\theta }_{1})\phi ({\theta }_{2})({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2}))-({\hat{\rho }}_{{\rm{a}}}({\theta }_{1})\phi ({\theta }_{1})-{\hat{\rho }}_{{\rm{a}}}({\theta }_{2})\phi ({\theta }_{2}))\\ {\nu }_{2} & := & p\mathrm{(1}-\phi ({\theta }_{1}\mathrm{))(1}-\phi ({\theta }_{2}))({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2}))\\ {\nu }_{1} & := & p({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2}))(\phi ({\theta }_{1})+\phi ({\theta }_{2})-2\phi ({\theta }_{1})\phi ({\theta }_{2}))\\ & & -({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2}))+({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})\phi ({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2})\phi ({\theta }_{2}))\\ {\nu }_{0} & := & p\phi ({\theta }_{1})\phi ({\theta }_{2})({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2}))-({\hat{\tau }}_{{\rm{a}}}({\theta }_{1})\phi ({\theta }_{1})-{\hat{\tau }}_{{\rm{a}}}({\theta }_{2})\phi ({\theta }_{2}\mathrm{)).}\end{array}$$

The reader is referred to Theorem 5 in Supplementary information, Part B for the calculation of the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$.

It is worth mentioning the above method can be less restrictive. For brevity, the details are available in Theorem 5 in Supplementary information, Part B.

Method K3: The apparent impedivity is measured in D ≥ 2 angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{d})$ and ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{2})$, and ${\theta }_{d}\in [\mathrm{0,}\,\pi )$

There are three different scenarios to estimate the anisotropy ratio ${\hat{\alpha }}^{2}$ and the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ (see Theorem 6 in Supplementary information, Part B), enumerated below:

• 1. ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1}\ne 0$ and ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2}\ne 0$:

  $${\hat{\alpha }}^{2}\,:\,={(\frac{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})-({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{2})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{1})\pm \sqrt{T}}{2({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})})}^{2}$$

  and

  $${\hat{\kappa }}_{\alpha }\,:\,=\frac{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{2})-({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{1})\mp \sqrt{T}}{\mathrm{2(}{{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})},$$

  (12)

• 2. ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1}=0$ and ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2}\ne 0$:

  $${\hat{\alpha }}^{2}\,:\,={(\frac{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{4})-({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{2})}{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{1})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})})}^{2}\,{\rm{and}}\,{\hat{\kappa }}_{\alpha }\,:\,=\frac{{{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4}}{{{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2}},$$

  (13)

• 3. ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1}\ne 0$, ${{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2}=0$:

$${\hat{\alpha }}^{2}\,:\,={(\frac{{{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4}}{{{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1}})}^{2}\,{\rm{and}}\,{\hat{\kappa }}_{\alpha }\,:\,=\frac{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{4})-({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{1})}{({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{2})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})},$$

(14)

and ${{\bf{a}}}_{1}\,:\,={[{a}_{11},{a}_{21},\cdots ,{a}_{D1}]}^{\top }$, ${{\bf{a}}}_{2}\,:\,={[{a}_{12},{a}_{22},\cdots ,{a}_{D2}]}^{\top }$, ${{\bf{a}}}_{3}\,:\,={[{a}_{13},{a}_{23},\cdots ,{a}_{D3}]}^{\top }$, ${{\bf{a}}}_{4}\,:\,={[{a}_{14},{a}_{24},\cdots ,{a}_{D4}]}^{\top }$, ${a}_{d1}\,:\,=p{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d})(\phi ({\theta }_{d})-1)$, a_d2: = pφ(θ_d) − 1, a_d3: = −p(φ(θ_d) − 1), ${a}_{d4}\,:\,=p{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d})\phi ({\theta }_{d})$, for $d=\mathrm{1,}\,\mathrm{2,}\,\cdots ,\,D$, and $T={(({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{4})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{3})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{2})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{1})+({{\bf{a}}}_{{3}^{\perp }}\cdot {{\bf{a}}}_{1})({{\bf{a}}}_{3}\cdot {{\bf{a}}}_{2}))}^{2}\,-\,\mathrm{4(}{{\bf{a}}}_{{3}^{\perp }}\,\cdot \,{{\bf{a}}}_{1})({{\bf{a}}}_{{3}^{\perp }}\,\cdot \,{{\bf{a}}}_{2})(({{\bf{a}}}_{3}\,\cdot \,{{\bf{a}}}_{1})({{\bf{a}}}_{3}\,\cdot \,{{\bf{a}}}_{2})\,+\,({{\bf{a}}}_{3}\,\cdot \,{{\bf{a}}}_{3})({{\bf{a}}}_{3}\,\cdot \,{{\bf{a}}}_{4})),$ and ${{\bf{a}}}_{{3}^{\perp }}$ is perpendicular to a₃.

Multiple inter-electrodes’ distances within the same needle and one measurement angle

Now, instead of keeping the inter-electrodes’ distances fixed while changing the measurement orientation (Fig. 12), we consider the case where the measurement angle is unique θ and the inter-electrodes’ distances change p_n (Fig. 13A). According to Fig. 13(B), the apparent impedivity κ_a based on (1) is

$${\kappa }_{{\rm{a}}}({p}_{n})={\kappa }_{\alpha }(1-\frac{1}{{p}_{n}\sqrt{{\cos }^{2}\theta +{\alpha }^{2}{\sin }^{2}\theta }}).$$

(15)

Figure 13

(A) Schematic showing the in situ measurement of anisotropic permittivity in N = 2 inter-electrodes’ distances using multipolar needles. N.b. compared to Fig. 12, there are more than one current and voltage electrodes in the z-direction within the same needle (in red and blue color, respectively). (B) Schematic of the n-th inter-electrodes’ distance measured in the z-direction. The measurement angle θ is defined with respect to the muscle fibers’ transverse (T) {x, z} direction ϕ_T (i.e. ϕ_T = θ when θ = 0) and ϕ_L is the longitudinal y direction. Electrode configuration: ${ {\mathcal E} }_{I}^{1}$, source current electrode; ${ {\mathcal E} }_{V}^{1}$, high potential electrode; ${ {\mathcal E} }_{V}^{n}$, low potential electrode; ${ {\mathcal E} }_{I}^{n}$, sink current electrode; where $n=\mathrm{2,}\,\mathrm{3,}\,\cdots ,\,N+1$ is the number of different inter-electrodes’ distances measured.

Method B1: The apparent impedivity is measured in $N=2$ inter-electrodes’ distances, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({p}_{1})$ and ${\kappa }_{{\rm{a}}}^{[m]}({p}_{2})$

The simplest case to estimate the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ and the anisotropy ratio ${\hat{\alpha }}^{2}$ is to measure the apparent impedivity with two different inter-electrodes’ distances (see Theorem 8 in Supplementary information, Part C), namely

$${\hat{\alpha }}^{2}\,:\,={({{\bf{q}}}^{\top }{\bf{q}})}^{-1}{{\bf{q}}}^{\top }{\bf{d}}\,{\rm{and}}\,{\hat{\kappa }}_{\alpha }\,:\,=\frac{{\hat{\kappa }}_{{\rm{a}}}({p}_{1}){p}_{1}-{\hat{\kappa }}_{{\rm{a}}}({p}_{2}){p}_{2}}{{p}_{1}-{p}_{2}},$$

(16)

where ${\bf{q}}\,:\,={[{p}_{1}^{2}{({\hat{\kappa }}_{\alpha }-{\hat{\kappa }}_{{\rm{a}}}({p}_{1}))}^{2}{\sin }^{2}\theta ,{p}_{2}^{2}{({\hat{\kappa }}_{\alpha }-{\hat{\kappa }}_{{\rm{a}}}({p}_{2}))}^{2}{\sin }^{2}\theta ]}^{\top }$ and ${\bf{d}}\,:\,=[{\hat{\kappa }}_{\alpha }^{2}-{p}_{1}^{2}{({\hat{\kappa }}_{\alpha }-{\hat{\kappa }}_{{\rm{a}}}({p}_{1}))}^{2}{\cos }^{2}\theta ,\,{\hat{\kappa }}_{\alpha }^{2}-\,{p}_{2}^{2}$${({\hat{\kappa }}_{\alpha }-{\hat{\kappa }}_{{\rm{a}}}({p}_{2}))}^{2}{\cos }^{2}\theta ]\top$, p₁: = g/h₁, and p₂: = g/h₂.

Method B2: The apparent impedivity is measured in N ≥ 2 inter-electrodes’ distances, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({p}_{n})$

Method B2 is the generalization of method B1 when N ≥ 2 inter-electrodes’ distances (see Theorem 9 in Supplementary information, Part C). The geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ and the anisotropy ratio ${\hat{\alpha }}^{2}$ can be estimated as follows

$${\hat{\alpha }}^{2}\,:\,=\frac{{x}^{2}-{y}^{2}{\cos }^{2}\theta }{{y}^{2}{\sin }^{2}\theta }\,{\rm{and}}\,{\hat{\kappa }}_{\alpha }:\,=x,$$

(17)

where ${[xy]}^{\top }\,:\,={({{\bf{B}}}^{\top }{\bf{B}})}^{-1}{{\bf{B}}}^{\top }{\bf{b}}$, ${\bf{b}}\,:\,={[{\hat{\kappa }}_{{\rm{a}}}({p}_{1}){\hat{\kappa }}_{{\rm{a}}}({p}_{2})\cdots {\hat{\kappa }}_{{\rm{a}}}({p}_{N})]}^{\top }$, and

$${\bf{B}}\,:\,=[\begin{array}{cc}1 & -\mathrm{1/}{p}_{1}\\ 1 & -\mathrm{1/}{p}_{2}\\ \vdots & \vdots \\ 1 & -\mathrm{1/}{p}_{N}\end{array}].$$

Multiple inter-electrodes’ distances within the same needle and multiple measurement angles

The reader may have noted that all previous methods require knowledge on the tissue’s anisotropic direction so that when θ = π/2 and θ = 0, the apparent impedivity measured is that corresponding to the anisotropic direction defined by the tissue, i.e. θ = ϕ_T when θ = 0 and consequently θ = ϕ_L when θ = π/2. Subsequently, experimental errors positioning the needle electrodes with respect the anisotropy in the permittivity of the tissue will give inaccurate estimates. We overcome this limitation by measuring the apparent impedivity with multiple electrodes’ depths and multiple measurement angles (see a sketch in Fig. 14A), namely

$${\kappa }_{{\rm{a}}}({\theta }_{d},{p}_{n})={\kappa }_{\alpha }(1-\frac{1}{{p}_{n}\sqrt{{\cos }^{2}({\theta }_{d}-\xi )+{\alpha }^{2}{\sin }^{2}({\theta }_{d}-\xi )}}),$$

(18)

where ξ is defined as the angle between the measurement axis and the true (unknown) anisotropy in the longitudinal and transverse permittivity of the tissue (see Fig. 14B).

Figure 14

(A) Schematic showing the in situ measurement of anisotropic permittivity in N ≥ 2 inter-electrodes’ distances and D ≥ 3 measurement angles using multipolar needles. (B) Schematic of the n-th depth and d-th angle measured. The measurement angle θ_d is defined with respect to the unknown muscle fibers’ transverse (T) {x, z} direction ϕ_T modeled by ξ (ϕ_L is the longitudinal y direction). Electrode configuration: ${ {\mathcal E} }_{I}^{(d-\mathrm{1)}\cdot N+1}$, source current electrode; ${ {\mathcal E} }_{V}^{(d-\mathrm{1)}\cdot N+1}$, high potential electrode; ${ {\mathcal E} }_{V}^{(d-\mathrm{1)}\cdot N+n}$, low potential electrode; ${ {\mathcal E} }_{I}^{(d-\mathrm{1)}\cdot N+n}$, sink current electrode; where $n=\mathrm{2,}\,\mathrm{3,}\,\cdots ,\,N$ and $d=\mathrm{1,}\,\mathrm{2,}\,\cdots ,\,D$ are the number of different electrodes’ depth and measurement angles measured, respectively.

Method S1: The apparent impedivity is measured in $N\ge 2$ inter-electrodes’ distances and $D\ge 3$ measurement angles, i.e. ${\kappa }_{{\rm{a}}}^{[m]}({\theta }_{d},{p}_{n})$

In this case, the geometric mean impedivity ${\hat{\kappa }}_{\alpha }$ can be estimated as follows (see Theorem 10 in Supplementary information, Part D),

$${\hat{\kappa }}_{\alpha }\,:\,=[1\,0\,0\,\cdots \,0]{({{\bf{S}}}^{\top }{\bf{S}})}^{-1}{{\bf{S}}}^{\top }{\bf{s}},$$

(19)

where ${\bf{s}}\,:\,={[{{\bf{s}}}_{1}{{\bf{s}}}_{2}\cdots {{\bf{s}}}_{D}]}^{\top }$ and ${{\bf{s}}}_{d}\,:\,=[{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d},{p}_{1}\mathrm{)\ }{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d},{p}_{2})\,\cdots \,{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d},{p}_{N})]$ for $d=\mathrm{1,}\,\mathrm{2,}\,\cdots ,\,D$ and S is an augmented matrix of size ND × (D + 1) defined as

$${\bf{S}}\,:\,=[\begin{array}{c}{{\bf{S}}}_{1}\\ {{\bf{S}}}_{2}\\ \vdots \\ {{\bf{S}}}_{D}\end{array}]\,{\rm{with}}\,{{\bf{S}}}_{d}\,:\,=[{\bf{1}}\,{{\bf{p}}}_{d1}\,{{\bf{p}}}_{d2}\,\cdots \,{{\bf{p}}}_{dt}\,\cdots \,{{\bf{p}}}_{dD}]$$

a block matrix of size N × (D + 1) made of column vectors ${\bf{1}}\,:\,={[11\cdots 1]}^{\top }$ and ${{\bf{p}}}_{dt}\,:\,={\delta }_{d,t}{[-1/{p}_{1}-1/{p}_{2}\cdots -1/{p}_{N}]}^{\top }$ with δ_d,t: = 1 if t = d else 0.

The estimated anisotropy ratio ${\hat{\alpha }}^{2}$ and anisotropy direction $\hat{\xi }$ can be estimated as follows

$${\hat{\alpha }}^{2}\,:\,=1-{\varpi }_{1}\,{\rm{or}}\,1-\sqrt{{\varpi }_{2}^{2}+{\varpi }_{3}^{2}}$$

(20)

and

$$\hat{\xi }\,:\,=\frac{1}{2}{\sin }^{-1}\frac{{\varpi }_{2}}{{\varpi }_{1}}\,{\rm{or}}\,\frac{1}{2}{\tan }^{-1}\frac{{\varpi }_{2}}{{\varpi }_{3}}\,{\rm{or}}\,\frac{1}{2}{\cos }^{-1}\frac{{\varpi }_{3}}{{\varpi }_{1}},$$

(21)

where ${[{\varpi }_{1}{\varpi }_{2}{\varpi }_{3}]}^{\top }\,:\,={({{\boldsymbol{\Xi }}}^{\top }{\boldsymbol{\Xi }})}^{-1}{{\boldsymbol{\Xi }}}^{\top }{\boldsymbol{\eta }}$,

$${\boldsymbol{\Xi }}\,:\,=[\begin{array}{ccc}1 & -\,\sin \,2{\theta }_{1} & -\,\cos \,2{\theta }_{1}\\ 1 & -\,\sin \,2{\theta }_{2} & -\,\cos \,2{\theta }_{2}\\ \vdots & \vdots & \vdots \\ 1 & -\,\sin \,2{\theta }_{D} & -\,\cos \,2{\theta }_{D}\end{array}],\,{\boldsymbol{\eta }}\,:\,=[\begin{array}{c}2-\mathrm{2/}{q}_{1}\\ 2-\mathrm{2/}{q}_{2}\\ \vdots \\ 2-\mathrm{2/}{q}_{D}\end{array}],$$

and

$${q}_{d}\,:\,=\frac{1}{N}{\sum }_{n=1}^{N}{p}_{n}^{2}{(\frac{{\hat{\kappa }}_{{\rm{a}}}({\theta }_{d},{p}_{n})}{{\hat{\kappa }}_{\alpha }}-1)}^{2}.$$