Introduction

Integrable models provide exact solutions for understanding some non-trivial physical phenomena in statistical physics, quantum field theory and condensed matter physics1,2,3,4. In general, integrable models can be divided into two classes: one possesses U(1) symmetry and the other does not. Previously, how to solve a model without U(1) symmetry is viewed as a formidable problem since a “local vacuum state” is not obvious. Recently, the authors of ref.5 have developed a systematic method called “off-diagonal Bethe Ansatz” (ODBA) to deal with it by adding an inhomogeneous term to the T − Q relation. The XXZ model with topological boundary condition is a typical integrable model without U(1) symmetry. The topological boundary condition not only makes the XXZ model lose U(1) symmetry but also endows it with some pretty unique properties. For instance, after a Jordan-Wigner transformation, it describes a p-wave Josephson junction embedded in a spinless Luttinger liquid6,7,8. Besides, each particle with momentum k must lock a hole with momentum −k to form a virtual bound state and thus the excitations of the topological XXZ model display topological nature9. The topological boundary condition can also profoundly affect quantum entanglement for the ground state of the XXZ model.

Quantum information science, as a new and developing research field, provides a variety of quantum correlations and enables us to capture the quantum characters of different quantum states in a mathematically rigorous fashion10,11,12,13,14,15,16,17,18,19,20,21,22. Entanglement is the first notion of quantum correlation to be discovered in 193523,24 and is used to describe the separability of a given quantum state. Nowadays, entanglement is widely accepted as a quantum resource as real as energy due to the rapid development of entanglement-based quantum technology, such as teleportation25,26, quantum cryptographic key distribution27, and quantum metrology28,29. Meanwhile, various entanglement measures were proposed in the past few decades. There are also other quantum correlation measures, e.g., the quantum discord which is defined by the differences between total correlation and classical correlation14.

The characteristics of quantum correlations for various integrable models were intensively studied30,31,32,33,34,35. The critical temperature Tc above which the thermal entanglement of the considered model vanishes was also introduced36. For example, Wang explored thermal entanglement of the XY model and found that Tc is independent of the strength of the transverse magnetic field B31,32,33. Further investigation shows that the critical temperature Tc may be enhanced when the external magnetic field is nonuniform34. In other words, it is possible to create entanglement in a high temperature environment under inhomogeneous magnetic field. Previous studies mainly focused on investigating entanglement of the integrable models with periodical boundary conditions37,38,39,40,41,42,43,44, while the role of other boundary conditions was usually neglected. With these considerations, we are prepared to expound how the topological boundary condition affects thermal entanglement and quantum discord in the XXZ model by comparing those with the case of periodical boundary condition.

This work is organized as follows. We introduce the XXZ model with periodical and topological conditions first. Then an analysis of the bipartite entanglement, bipartite discord, tripartite entanglement, and critical temperature for them are carried out. The differences between quantum correlations in the XXZ model with periodical and topological conditions are compared in detail, through which it was found that the topological boundary condition is beneficial for the protection of entanglement against thermal fluctuations in the considered model. Last, we summarize our main conclusions.

Results

The XXZ Model

The Hamiltonian of the three-qubit XXZ model with nonuniform external magnetic fields reads

$$H=\sum _{i=1}^{3}\,[J({\sigma }_{i}^{x}{\sigma }_{i+1}^{x}+{\sigma }_{i}^{y}{\sigma }_{i+1}^{y})+{J}_{z}{\sigma }_{i}^{z}{\sigma }_{i+1}^{z}]+(B+b){\sigma }_{1}^{z}+B{\sigma }_{2}^{z}+(B-b){\sigma }_{3}^{z},$$
(1)

where σα (α = x, y, z) are the Pauli operators. J and Jz represent strength of the spin coupling, and B controls strength of external magnetic field along the z-direction. The parameter b is introduced to describe the inhomogeneity of magnetic field.

We consider two kinds of boundary conditions in this work, see Fig. 1. One is the periodical boundary condition (\({\sigma }_{4}^{\alpha }={\sigma }_{1}^{\alpha }\), α = x, y, z), and the other is the topological boundary condition (\({\sigma }_{4}^{\alpha }={\sigma }_{1}^{x}{\sigma }_{1}^{\alpha }{\sigma }_{1}^{x}\), α = x, y, z). For such a topological boundary condition, the spin on the last site connects with that on the first site after rotating a π angle along the x direction and thus forms a quantum Möbius strip in the spin space. This model is not only physically non-trivial due to its relevance to the realization of topological matter, but also non-trivial in solving due to its lack of the U(1) symmetry. By using the ODBA method, the exact solution of the topological XXZ model is obtained in ref. 9. However, the expressions of eigenstates given by ODBA method are complicated. Thus, we directly adopt the exact diagonalization method to obtain the energy spectrum (Ei) and the eigenstates (|Ψi〉) of the topological and the periodical XXZ model. The thermal equilibrium state of topological and periodical XXZ model can then be constructed by their energy spectrum and eigenstates as follows

$$\rho (T)=\frac{1}{Z}\,\sum _{i=1}^{8}\,{e}^{-\beta {E}_{i}}|{{\rm{\Psi }}}_{i}\rangle \langle {{\rm{\Psi }}}_{i}|,$$
(2)

where β = 1/kBT, Z = Tr(e−βH) is the partition function of the system, and the Boltzmann’s constant kB will be set to 1 hereafter.

Figure 1
figure 1

Two different boundary conditions. The periodical XXZ spin ring is denoted by PSR and the topological XXZ spin ring is denoted by TSR.

Full size image

Quantum correlations of the XXZ model

We examine bipartite and tripartite correlations for thermal states of the three-qubit XXZ model, aimed at revealing effects of topological boundary condition on improving strength of the considered correlation and the corresponding critical temperature Tc. The quantum correlations we considered are the bipartite entanglement quantified by concurrence Cij, the bipartite discord quantified by modified geometric discord GDij, and the tripartite entanglement quantified by negativity. The subscript (ij) denotes the bipartite quantum correlations between the i-th spin and the j-th spin.

Bipartite entanglement

The most basic entanglement measure is the entanglement of formation, which is intended to quantify the resources needed to create a given entangled state45. Concurrence is an entanglement-of-formation measure which applies for two-qubit states. It is defined as46

$$C(\rho )=\,{\rm{\max }}\,\{{\lambda }_{1}-{\lambda }_{2}-{\lambda }_{3}-{\lambda }_{4},0\},$$
(3)

where λi are square roots of the eigenvalues of the matrix \(\rho \tilde{\rho }\) with \({\lambda }_{1}\geqslant {\lambda }_{2}\geqslant {\lambda }_{3}\geqslant {\lambda }_{4}\). \(\tilde{\rho }=({\sigma }^{y}\otimes {\sigma }^{y}){\rho }^{\ast }({\sigma }^{y}\otimes {\sigma }^{y})\) and ρ* is the complex conjugate of ρ. The concurrence C = 0 corresponds to an unentangled state while C = 1 corresponds to a maximally entangled state.

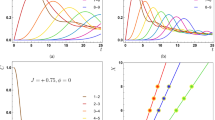
Figure 2 shows dependence of C12, C23 and C13 on external magnetic fields B and b, from which one can note that the behaviors of C12 and C23 with different boundary conditions are similar. The boundary conditions only significantly affect entanglement between the boundary spins 1 and 3. For the periodical case, the concurrence for thermal states of the boundary spins can exist for a highly inhomogeneous magnetic field (large b) but it is easily to be destroyed by increasing the strength of magnetic field (large B), see Fig. 2(c′). For the topological case, it is just the opposite. Therefore, the differences induced by different boundary conditions mainly lie in the boundary spins, and we will concentrate on investigating behaviors of quantum correlations for them.

Figure 2
figure 2

Concurrence versus B and b in the topological XXZ model and the periodical XXZ model with T = 1, J = 1 and Jz = 1.5. The maximum values of concurrence are 0.85, 0.85 and 0.32 for the topological case (a–c)] and 0.61, 0.61 and 0.28 for the periodical case (a′–c′).

Full size image

It is also worth noting that the maximal values of concurrence for the topological boundary condition case are always larger than those for the periodical boundary condition case. In particular, the boundary spins of the XXZ model with topological boundary condition possess bipartite entanglement even with B = 0, while this is not the case for that with the periodical boundary condition. These facts imply that a system with topological boundary condition may lead to more robust bipartite entanglement than a system with periodical boundary condition. The calculation of C13 versus T also support the above conjecture, e.g., from Fig. 3(a) one can found that the concurrence for the boundary spins with topological boundary condition is significantly larger than that with periodical boundary condition, whether it is at high temperature or low temperature.

Figure 3
figure 3

(a) Concurrence of the boundary spins C13 versus temperature T in the topological XXZ model and the periodical XXZ model with J = 1 and Jz = 1.5. The blue dash line coincide with horizontal axis. (b) Critical temperature Tc of concurrence C13 versus the strength of magnetic field B in the topological XXZ model and the periodical XXZ model with J = 1 and Jz = 1.5.

Full size image

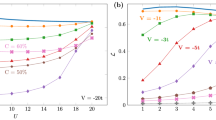
The critical temperature Tc above which C13 vanishes was plotted in Fig. 3(b). It is clear that Tc for the case of topological boundary condition is higher than that for the case of periodical boundary condition. Moreover, Tc of C13 with topological boundary condition can be increased by increasing the strength of magnetic field B, which is not feasible for the periodical boundary condition case. In other words, by applying a sufficiently strong magnetic field B, the bipartite entanglement can be stored in the topological boundary spins at high temperature, whereas the periodical boundary spins do not have this advantage.

Figure 4 gives the scaling behavior of Tc of boundary spin’s concurrence versus the system size N, one can note that Tc of topological boundary spin’s concurrence is always higher than that of periodical case. Thus the topological boundary condition can protect bipartite entanglement against thermal fluctuations no matter how long the spin chain is.

Figure 4
figure 4

The scaling behavior of critical temperature Tc of boundary spin’s concurrence against the system size N with J = 1, Jz = 1.5, B = 3 and b = 0. The asymptotic value is 4.24 for TSR and 3.74 for PSR.

Full size image

Bipartite quantum discord

Previous studies have shown that lots of quantum tasks could be realized successfully without entanglement. Then the quantum discord, which was defined as the differences between quantum mutual information and classical correlation, was introduced to measure the total amount of quantum correlations, thus it can characterize nonclassicality of correlations. The quantum discord defined in ref.14 is difficult to calculate even for general two-qubit states. In 2010, Dakić et al. proposed the geometric discord47, then the modified geometric discord was put forward where the density operator of the geometric discord was replaced by the square root of density operator48

$$GD({\rho }^{ab})=\mathop{{\rm{\min }}}\limits_{{{\rm{\Pi }}}^{a}}{\Vert \sqrt{{\rho }^{ab}}-{{\rm{\Pi }}}^{a}(\sqrt{{\rho }^{ab}})\Vert }^{2},$$
(4)

where the min is taken over all local von Neumann measurements \({{\rm{\Pi }}}^{a}=\{{{\rm{\Pi }}}_{k}^{a}\}\) on party a, ||·|| denotes the Hilbert-Schmidt norm, and

$${{\rm{\Pi }}}^{a}(\sqrt{{\rho }^{ab}}):\,=\sum _{k}\,({{\rm{\Pi }}}_{k}^{a}\otimes { {\mathcal I} }^{b})\sqrt{{\rho }^{ab}}({{\rm{\Pi }}}_{k}^{a}\otimes { {\mathcal I} }^{b}).$$
(5)

Figure 5 shows modified geometric discord for different spin pairs of the XXZ model with periodical and topological boundary conditions, from which one can observe quantitatively the similar behaviors to those of bipartite entanglement: (1) the boundary spins are the main objects to bear the influence of different boundary conditions; (2) the topological boundary spins can store bipartite discord in the region of strong magnetic field B; (3) the periodical boundary spins can store bipartite discord in the region of strong inhomogeneous magnetic field b; (4) the maximal values of bipartite discord under topological boundary condition are larger than those under periodical boundary condition. Different from quantum entanglement, the quantum discord disappears only in the infinite temperature, and there does not exist a critical temperature Tc. But the discord under topological boundary condition is always larger than that under the periodical boundary condition, see Fig. 6.

Figure 5
figure 5

Modified geometric discord versus B and b in the topological XXZ model and the periodical XXZ model with T = 1, J = 1 and Jz = 1.5. The maximum values of discord are 0.32, 0.32 and 0.11 for the topological case (a–c)] and 0.16, 0.16 and 0.04 for the periodical case (a′–c′).

Full size image
Figure 6
figure 6

Modified geometric discord of the boundary spins GD13 versus temperature T in the topological XXZ model and the periodical XXZ model with J = 1 and Jz = 1.5.

Full size image

Tripartite entanglement

Tripartite negativity49 is applied to measure tripartite entanglement in this work. It was defined as

$$N(\rho )=\sqrt[3]{({N}_{A-BC}{N}_{B-CA}{N}_{C-AB})},$$
(6)

where

$${N}_{i-jk}=\frac{1}{2}\,[\sum _{l}\,|{\lambda }_{l}({\rho }^{{T}_{i}})|\,-\,1],$$
(7)

and \({\lambda }_{l}({\rho }^{{T}_{i}})\) are eigenvalues of the partial transposed density martrix \({\rho }^{{T}_{i}}\) of the composite system with respect to subsystem i.

In Fig. 7, we showed dependence of negativity on B and b. There are two triangular regions representing strong magnetic fields B where the negativity vanishes for the case of periodical boundary condition while exists for the case of topological boundary condition. It means that the tripartite entanglement can exist in the region of strong magnetic field for the topological XXZ model.

Figure 7
figure 7

Negativity versus B and b in the topological XXZ model and the periodical XXZ model with T = 1, J = 1 and Jz = 1.5. The maximum value of negativity is 0.27 for the topological case (a) and 0.25 for the periodical case (b).

Full size image

The previous researches31,32,33,34 show that the critical temperature Tc for the periodical XY model can be enhanced with a nonuniform magnetic field b but remains unchanged with increasing magnetic field B. For the periodical XXZ model, the same phenomenon is also found, see Fig. 8. It is unexpected that two completely different models show the similar properties. On the contrary, in addition to a nonuniform magnetic field, the topological boundary condition allows us to improve Tc for the XXZ model via another approach, i.e., increasing the strength of magnetic field B. There is another interesting phenomenon that Tc of tripartite entanglement is higher than Tc of bipartite entanglement in periodical XXZ model. Nevertheless, in the topological XXZ model, Tc of tripartite entanglement will lower than Tc of bipartite entanglement. This indicates that there is a region in the topological XXZ model where bipartite entanglement exists but tripartite entanglement vanishes. For the periodical XXZ model, there is a region in which the existence of tripartite entanglement is a necessary condition for existence of bipartite entanglement.

Figure 8
figure 8

(a) Critical temperature Tc of negativity versus the strength of magnetic field B in the topological XXZ model and the periodical XXZ model with J = 1 and Jz = 1.5. (b) Critical temperature Tc of negativity versus the inhomogeneity of magnetic field b in the topological XXZ model and the periodical XXZ model with J = 1 and Jz = 1.5.

Full size image

Discussion

In this work, the three-qubit XXZ model with periodical and topological boundary conditions have been investigated by calculating their bipartite entanglement, bipartite discord, tripartite entanglement, and corresponding critical temperature. The results reveal that the different boundary conditions mainly affect bipartite quantum correlations of the boundary spins instead of other spin pairs. In the region of strong magnetic field B, the bipartite entanglement and bipartite discord can be stored in the topological boundary spins. On the contrary, the XXZ model with periodical boundary condition is conducive to storing bipartite entanglement and bipartite discord in a nonuniform magnetic field.

Generally speaking, the topological boundary condition protects entanglement against thermal fluctuations in the XXZ model because critical temperature of bipartite entanglement in the topological boundary spins is always higher than that in the periodical boundary spins, even when the system size N grows. Moreover, the critical temperatures of tripartite entanglement in the topological XXZ model are all higher than those in the periodical XXZ model. The topological boundary condition also allows us to improve critical temperature by the following two approaches: increasing the strength of magnetic field B or the inhomogeneity of magnetic field b. However, increasing the strength of magnetic field is useless for improving the critical temperature of the periodical XXZ model, especially for the case of tripartite entanglement. From this point, the periodical XXZ model is similar to the periodical XY model. Another interesting finding is that there is a region for the topological XXZ model where bipartite entanglement exists but tripartite entanglement vanishes.

Topological boundary condition not only breaks the U(1) symmetry making the XXZ model hard to solve but also protects the entanglement against thermal fluctuations. Besides, we can increase the strength of magnetic field to make entanglement alive at relatively high temperature, which is impossible for the periodical case. We believe that systems with topological boundary condition will exhibit their unique properties in entanglement-based quantum information technologies. In particular, it would be interesting to make a thorough calculation for the case of infinite topological XXZ chain via ODBA method.