Introduction

The study of flow in ducts with permeable walls is of great practical interest both in engineering as well as bio-physical flows1,2,3,4. Many processes like membrane filtration, transpiration cooling, blood flow, gaseous diffusion in binary mixtures, renal flow and artificial dialysis are the examples of flows in permeable ducts.

A large number of investigators paid attention towards the experimental and theoretical models of filtration processes. Berman5 was the first to study the effect of suction/injection at the permeable wall of the channel. He used similarity solutions along with the perturbation method to analyze the velocity and pressure fields. Yuan et al.6,7 obtained perturbation solutions for small and large suction Reynolds number by extending the work of Berman5. Terrill8 found out exact solution for the problem of flow in a porous pipe.

Many authors studied the problem of flow in permeable ducts in context of its application to flow in renal tubule. Macey9 determined the solution of a flow problem of viscous fluid through a circular tube by considering linear reabsorption rate at the wall. Kelman10 pointed out that the bulk flow rate decays exponentially with the axial distance in renal tubule. Macey11 used this condition and observed the parabolic axial velocity profile and found out that mean pressure drop was proportional to the mean axial flow. Marshal and Trowbridge12 solved the same problem by making use of physical conditions instead of prescribing flux as a function of downstream distance.

To study the flow problems, authors frequently used the no-slip condition at the solid boundaries. However, this assumption is an idealization and has no empirical justification when fluid flows over a permeable boundary. Many investigators has now accepted that a large class of polymeric materials slip or stick-slip on the solid boundaries. Rao and Rajagopal13 studied the flows of a Johnson-Segalman fluid and explained spurt and observed the effects of the slip condition on the flow of Newtonian fluid. Moustafa14 illustrated the significance of slip at the wall. It has been justified from literature15 that the slip velocity is linearly proportional to the shear rate at the wall. Actually, slip velocity is connected to the thin layer of the fluid that is flowing streamwise just below the permeable wall. The fluid present in this layer is considered to be pulled along by the fluid above the permeable wall. Further, slip is useful in many other applications16,17,18,19.

Application of magnetohydrodynamics has become quite helpful in various biological problems like in the treatment of different cancer diseases. It is also applicable in engineering problems like electromagnetic casting, plasma confinement and continuous casting process of metals etc. Magnetic field has great influence on the flow of blood. For instance, influence of magnetic field on blood flow is reported by Sinha and Misra20. Sud et al.21 studied the influence of moving magnetic field on the flow of blood. Recently a technology known as nano particles separation technology is studied by many authors. This technology shows that magnetic field can be used to isolate nano particles from plasma with minimum manipulation22.

A bulk of literature dealt with the consideration of constant flow rate in permeable ducts. However this is not a good choice for analyzing the flow problems which may have non-uniform normal flow at the walls. Recently authors23,24 studied the behavior of physiological flows in various geometries by taking into consideration the variable bulk flow rate due to non-uniform flux at the walls. They used both analytical as well as numerical methods to investigate the effects of different parameters on the flow.

Many researchers25,26 worked on blood flow problems in tubes by applying Adomian decomposition method (ADM). This method was developed by Adomian27. ADM provides an accurate and computable solutions of the flow problems for sufficiently small number of terms and is proved to be parallel to any supercomputer. The advantage of this method is avoidance of the simplifications which may change the physical behavior of the flow models. It attacks the problems in a straightforward manner without perturbation, linearization and any restrictive assumptions resulting in physically more realistic solutions27,28,29,30,31.

In preceding studies, authors considered the channels/tubes of uniform cross-section. But in general, cross-section of renal tubule may vary along its length. Radhakrishnamacharya et al.32 studied the hydrodynamical aspects of viscous fluid flow in renal tubule by considering it to be a circular tubule of non-uniform cross-section. Chandra and prasad33 done the same problem by using starling’s hypothesis. Recently Muthu and Tefshan34 studied reabsorption process from the wall of a channel with non-uniform cross-section. Later on Muthu and Teshfa35 extended the work34 by including the slip effects.

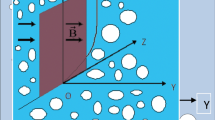
The increasing number of applications of biophysical and industrial flows mentioned above force us to extend already available hydrodynamic solutions to encircle all possible issues and tackle them with appropriate analytical technique. Keeping in view the above studies, the objective of this study is to understand the hydrodynamics of flow of the viscous fluid through a non-uniform channel with slip at permeable wall under the influence of magnetic field. This analysis is carried out by considering flux as a decreasing function of downstream distance. The half-height h′(x′) of the channel is assumed to vary with axial distance in the following manner

$$h^{\prime} (x^{\prime} )={h}_{0}+{m}_{1}x^{\prime} +bsin(\frac{2\pi x^{\prime} }{\lambda }),$$
(1)

where m1 is the slop parameter which depends on the inlet and exit dimensions, b is the amplitude, λ is the wave length and h0 is the half height of the channel at x = 0 (see Fig. 1).

Figure 1
figure 1

Schematic diagram of flow through a non-uniform channel.

Full size image

Full Navier-Stokes equations are solved with non-zero Reynolds number. Influence of reabsorption parameter (α), slip coefficient coefficient (ϕ) and slop parameter (m) on various flow variables in the presence of transverse magnetic field is the main concern of this study. Present work provides a more general form of solution from which already available solutions in literature can be deduced by proper substitutions of pertinent parameters. This study provides a useful information in improving the models for solving different biophysical and engineering problems. Proper knowledge of flow behavior under the influence of magnetic field may be useful in magnetic or electromagnetic therapy as well as in many engineering problems.

Problem Formulation

Consider a steady flow of an incompressible Newtonian fluid through a permeable channel with slowly varying cross section under the influence of transverse magnetic field. We assume that the induced magnetic field is neglected due to very small magnetic Reynolds number. The half-height of the channel at its inlet is h0. However it varies along the length of the channel. A rectangular coordinate system (x′, y′) is chosen, in which is x′ taken along the axis of the channel and y′ is being normal to it. The volume flow rate is assumed to vary with the downstream distance (see Fig. 1).

The rheological equations of motion governing the flow are given as:

$$\frac{\partial u^{\prime} }{\partial x^{\prime} }+\frac{\partial v^{\prime} }{\partial y^{\prime} }=0,$$
(2)
$$\rho (u^{\prime} \frac{\partial u^{\prime} }{\partial x^{\prime} }+v^{\prime} \frac{\partial u^{\prime} }{\partial y^{\prime} })=-\,\frac{\partial p^{\prime} }{\partial x^{\prime} }+\mu (\frac{{\partial }^{2}u^{\prime} }{\partial x{^{\prime} }^{2}}+\frac{{\partial }^{2}u^{\prime} }{\partial y{^{\prime} }^{2}})-\sigma {B}_{0}^{2}u^{\prime} ,$$
(3)
$$\rho (u^{\prime} \frac{\partial v^{\prime} }{\partial x^{\prime} }+v^{\prime} \frac{\partial v^{\prime} }{\partial y^{\prime} })=-\,\frac{\partial p^{\prime} }{\partial x^{\prime} }+\mu (\frac{{\partial }^{2}v^{\prime} }{\partial x{^{\prime} }^{2}}+\frac{{\partial }^{2}v^{\prime} }{\partial y{^{\prime} }^{2}}),$$
(4)

where u′(x′, y′) and v′(x′, y′) are the axial and transverse components of velocity respectively, ρ, μ and p′(x′, y′) are the constant density, viscosity and pressure of the fluid respectively σ and B0 are the electrical conductivity and transverse component of magnetic field respectively. The appropriate boundary conditions for the problem under consideration are

Regularity condition:

$$\frac{\partial u^{\prime} }{\partial y^{\prime} }=0,\,v^{\prime} =0\,{\rm{at}}\,y^{\prime} =0.$$
(5)

Slip at the boundary:

$$u^{\prime} +\frac{\partial h^{\prime} }{\partial x^{\prime} }v^{\prime} =-\,\varphi ^{\prime} (\frac{\partial u^{\prime} }{\partial y^{\prime} }+\frac{\partial h^{\prime} }{\partial x^{\prime} }\frac{\partial v^{\prime} }{\partial y^{\prime} })\,{\rm{at}}\,y^{\prime} =h^{\prime} (x^{\prime} ).$$
(6)

Bulk flow rate is assumed to be a decreasing function of downstream distance,

$$\,Q^{\prime} (x^{\prime} )=2{\int }_{0}^{h^{\prime} (x^{\prime} )}u^{\prime} dy^{\prime} ={Q}_{0}F(\alpha ^{\prime} x^{\prime} ).$$
(7)

Pressure at the inlet of the channel is

$$\,p^{\prime} (x^{\prime} ,y^{\prime} )=p{^{\prime} }_{0},\,{\rm{at}}\,x^{\prime} =0,\,y^{\prime} =0.$$
(8)

In above equations, \(\varphi ^{\prime} =\sqrt{\frac{\gamma ^{\prime} }{\beta }}\) is the slip coefficient, in which γ′ is the permeability of the wall and β is a dimensionless constant which depends on the characteristics of the wall. F(α′x′) = 1 for α′ = 0 and decreases with x′; α′ ≥ 0 is constant reabsorption coefficient; Q0 is the constant flux across the cross-section at x′ = 0 and h′(x′) is the non-uniform boundary given in Eq. (1).

Introducing the following dimensionless quantities

$$\begin{array}{c}x=\frac{x^{\prime} }{\lambda },\,y=\frac{y^{\prime} }{{h}_{0}},\,u=\frac{{h}_{0}}{{Q}_{0}}u^{\prime} ,\,v=\frac{\lambda }{{Q}_{0}}v^{\prime} ,\\ \,\delta =\frac{{h}_{0}}{\lambda },\,\alpha =\alpha ^{\prime} \lambda ,\,h(x)=\frac{h^{\prime} (x^{\prime} )}{{h}_{0}},\end{array}\}$$
(9)

where δ is the wall variation parameter (ratio of inlet half width to the length of the channel). Eqs (1–3) become

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$
(10)
$$Re\delta (u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y})=-\,\frac{\partial p}{\partial x}+{\delta }^{2}\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}-{H}^{2}u,$$
(11)
$$Re{\delta }^{3}(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y})=-\,\frac{\partial p}{\partial x}+{\delta }^{2}({\delta }^{2}\frac{{\partial }^{2}v}{\partial {x}^{2}}+\frac{{\partial }^{2}v}{\partial {y}^{2}}),$$
(12)

where \(Re=\frac{{Q}_{0}}{\upsilon }\) and \(H={B}_{0}{h}_{0}\sqrt{\frac{\sigma }{\mu }}\) are the Reynolds number and Hartman number respectively and

\(p=\frac{{h}_{0}^{2}}{\mu {Q}_{0}}p^{\prime} \) is the dimensionless pressure.

Boundary conditions (4–7), in dimensionless form are

$$\frac{\partial u}{\partial y}=0,\,v=0,\,{\rm{at}}\,y=0,$$
(13)
$$u+{\delta }^{2}\frac{\partial h}{\partial x}v=-\,\varphi (\frac{\partial u}{\partial y}+{\delta }^{2}\frac{\partial h}{\partial x}\frac{\partial v}{\partial y})\,{\rm{at}}\,y=h(x),$$
(14)
$$Q(x)=2{\int }_{0}^{h(x)}\,udy=F(\alpha x),$$
(15)
$$p(x,y)={p}_{0},\,{\rm{at}}\,x=0,\,y=0,$$
(16)

where

$$\varphi =\frac{\varphi ^{\prime} }{{h}_{0}},\,{\epsilon }=\frac{b}{{h}_{0}},\,m=\frac{{m}_{1}\lambda }{{h}_{0}}.$$
(17)

In rectangular coordinates, stream function is defined as

$$u=\frac{\partial \psi (x,y)}{\partial y},\,v=\frac{\partial \psi (x,y)}{\partial x}.$$
(18)

Making use of Eq. (18) into Eqs (10–12) and eliminating p between Eqs (11) and (12), we get the following compatibility equation

$${\nabla }^{4}\psi =Re\delta [\frac{\partial \psi }{\partial y}\frac{\partial }{\partial x}({\nabla }^{2}\psi )-\frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}({\nabla }^{2}\psi )]-{H}^{2}\frac{{\partial }^{2}\psi }{\partial {y}^{2}},$$
(19)

where

$${\nabla }^{2}={\delta }^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{{\partial }^{2}}{\partial {y}^{2}}.$$

Boundary conditions (13–15) take the following form

$$\frac{{\partial }^{2}\psi }{\partial {y}^{2}}=0,\,\frac{\partial \psi }{\partial x}=0\,{\rm{at}}\,y=0,$$
(20)
$$\frac{\partial \psi }{\partial y}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{\partial \psi }{\partial x}=-\,\varphi (\frac{{\partial }^{2}\psi }{\partial {y}^{2}}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{{\partial }^{2}\psi }{\partial x\partial y}),\,{\rm{at}}\,y=h(x),$$
(21)
$$Q(x)=2{\int }_{0}^{h(x)}\,\frac{\partial \psi }{\partial y}dy=F(\alpha x),$$
(22)

We take F(αx) = e−αx. This assumption is important physiologically as pointed out by Kelman10 and used by various authors11,15,16.

The problem is now reduced to a fourth order, non-linear partial differential Eq. (19) with non-homogeneous boundary conditions (20–22). Approximate analytical solution of the problem is presented in the next section.

Solution of the problem

The solution of the problem (19–22) is obtained using Adomian decomposition method as follows27,28,29,30,31.

Consider \(L=\frac{{\partial }^{2}}{\partial {y}^{2}}\) to be a linear operator. Then Eq. (19) can be rewritten in the following form

$${L}^{2}\psi =Re(N\psi )-\frac{{\partial }^{4}\psi }{\partial {x}^{4}}-2L\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+{H}^{2}\frac{{\partial }^{2}\psi }{\partial {y}^{2}},$$
(23)

where

$$N\psi =\frac{\partial \psi }{\partial y}\frac{\partial }{\partial x}({\nabla }^{2}\psi )-\frac{\partial \psi }{\partial x}\frac{\partial }{\partial y}({\nabla }^{2}\psi ),$$
(24)

is the nonlinear term.

Operating L−2 on both sides of Eq. (23), we get

$$\psi ={\psi }_{0}+{L}^{-2}[Re(N\psi )-\frac{{\partial }^{4}\psi }{\partial {x}^{4}}-2L\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+{H}^{2}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}],$$
(25)

Remembering that boundary condition terms vanish, operator L−2 is the two fold pure integral defined as

$${L}^{-2}=\iint \iint (.\,)dydydydy,$$
(26)

and ψ0 is the solution of homogeneous equation Lψ = 0 which is given below

$${\psi }_{0}(x,y)=a(x){y}^{3}+b(x){y}^{2}+c(x)y+d(x)$$
(27)

where a(x), b(x), c(x) and d(x), are constants which are to be determined from boundary conditions.

Decomposing u, Nψ and ψ0 as follows28

$$\psi =\sum _{n=0}^{\infty }\,{\psi }_{n},\,N\psi =\sum _{n=0}^{\infty }\,{A}_{n},\,{\psi }_{0}=\sum _{n=0}^{\infty }\,{\psi }_{0,n},$$
(28)

where An’s are the Adomian polynomials and we have applied double decomposition28. Using Eq. (28) into Eq. (25), we arrive at

$${\psi }_{n+1}={\psi }_{0,n+1}+{L}^{-2}[Re{A}_{n}-\frac{{\partial }^{4}\psi }{\partial {x}^{4}}-2L\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+{H}^{2}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}],$$
(29)

From Eqs (27) and (28), we may write

$${y}_{0,n+1}(x,y)={a}_{n}(x){y}^{3}+{b}_{n}(x){y}^{2}+{c}_{n}(x)y+{d}_{n}(x)$$
(30)

where the constants are also decomposed as

$$a(x)=\sum _{n=0}^{\infty }\,{a}_{n}(x),\,b(x)=\sum _{n=0}^{\infty }\,{b}_{n}(x),\,c(x)=\sum _{n=0}^{\infty }\,{c}_{n}(x),\,d(x)=\sum _{n=0}^{\infty }\,{d}_{n}(x)$$
(31)

From Eq. (29), we have

$${\psi }_{1}={\psi }_{0,1}+{L}^{-2}[Re{A}_{0}-\frac{{\partial }^{4}\psi }{\partial {x}^{4}}-2L\frac{{\partial }^{2}\psi }{\partial {x}^{2}}+{H}^{2}\frac{{\partial }^{2}\psi }{\partial {y}^{2}}],$$
(32)

where

$${\psi }_{0,1}(x,y)={a}_{1}(x){y}^{3}+{b}_{1}(x){y}^{2}+{c}_{1}(x)y+{d}_{1}(x)$$
(33)

In above equations, Adomian polynomials A0, A1, A2, ... An are generated in such way28 that

$$\begin{array}{c}{A}_{0}\equiv {A}_{0}({\psi }_{0}),\,{A}_{0}\equiv {A}_{0}({\psi }_{0},{\psi }_{1}),\\ \,\,\,\,\,{A}_{2}\equiv {A}_{2}({\psi }_{0,},{\psi }_{1},{\psi }_{2}),\ldots {A}_{n}\equiv {A}_{n}({\psi }_{0,},{\psi }_{1},{\psi }_{2},\ldots {\psi }_{n}).\end{array}$$
(34)

Using Eq. (28) into Eq. (24), we can write

$${A}_{n}=\frac{\partial {\psi }_{n}}{\partial y}\frac{\partial ({\nabla }^{2}{\psi }_{n})}{\partial x}-\frac{\partial {\psi }_{n}}{\partial x}\frac{\partial ({\nabla }^{2}{\psi }_{n})}{\partial y},$$
(35)

From where, we get

$${A}_{0}=\frac{\partial {\psi }_{0}}{\partial y}\frac{\partial ({\nabla }^{2}{\psi }_{0})}{\partial x}-\frac{\partial {\psi }_{0}}{\partial x}\frac{\partial ({\nabla }^{2}{\psi }_{0})}{\partial y},$$
(36)

Further, boundary conditions (20–22) take the following form

$$\begin{array}{c}{\psi }_{0}=0,\,\frac{{\partial }^{2}\,{\psi }_{0}}{\partial {y}^{2}}=0,\,\frac{\partial \,{\psi }_{0}}{\partial x}=0\,{\rm{at}}\,y=0,\\ \frac{\partial \,{\psi }_{0}}{\partial y}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{\partial \,{\psi }_{0}}{\partial x}=-\,\varphi (\frac{{\partial }^{2}\,{\psi }_{0}}{\partial {y}^{2}}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{{\partial }^{2}{\psi }_{0}}{\partial x\partial y}),\,{\rm{at}}\,y=h(x),\end{array}$$
(37)
$$\begin{array}{c}{\psi }_{1}=0,\,\frac{{\partial }^{2}\,{\psi }_{1}}{\partial {y}^{2}}=0,\,\frac{\partial \,{\psi }_{1}}{\partial x}=0\,{\rm{at}}\,y=0,\\ \frac{\partial {\psi }_{1}}{\partial y}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{\partial {\psi }_{1}}{\partial x}=-\,\varphi (\frac{{\partial }^{2}{\psi }_{1}}{\partial {y}^{2}}-{\delta }^{2}\frac{\partial h}{\partial x}\frac{{\partial }^{2}{\psi }_{1}}{\partial x\partial y}),\,{\rm{at}}\,y=h(x),\end{array}$$
(38)

From Eqs (33) and (37), we get ψ0 as

$${\psi }_{0}=f(x){y}^{3}+g(x)y$$
(39)

where

$$\begin{array}{c}f(x)=\frac{{e}^{-\alpha x}[1+\alpha {\delta }^{2}{h}_{1}(\varphi +h)]}{2{h}^{2}(3\varphi +h+\alpha {\delta }^{2}\varphi h{h}_{1})}\\ g(x)=\frac{{e}^{-\alpha x}[3h(h+2\varphi )+1+\alpha {\delta }^{2}{h}^{2}{h}_{1}(3\varphi +h)]}{2{h}^{2}(3\varphi +h+\alpha {\delta }^{2}\varphi h{h}_{1})}\end{array}$$
(40)

ψ1 can be determined from Eqs (32), (33), (39) and (40) as given below

$$\psi 1=a1(x)y3+b1(x)y2+c1(x)y+d1(x)+{\rm{\Omega }}(x){y}^{9}+\eta (x){y}^{7}+\xi (x){y}^{5},$$
(41)

where

$${\rm{\Omega }}(x)=-\,\frac{Re{\delta }^{2}}{1008}[{f}_{1}{f}_{2}-f{f}_{3}],$$
(42)
$${\rm{\eta }}(x)=\frac{1}{840}[Re(12f{f}_{1}+{\delta }^{2}(3f{g}_{3}-3{g}_{1}\,{f}_{2}-{f}_{1}{g}_{2}+g{f}_{3}))-{\delta }^{4}{{\rm{f}}}_{4}],$$
(43)
$$\xi (x)=\frac{1}{120}[Re(g(6{f}_{1}+{\delta }^{2}{g}_{3})-{g}_{1}(6f+{\delta }^{2}{g}_{2}))-{\delta }^{2}(12{f}_{2}+{g}_{4})+6{H}^{2}f].$$
(44)

In above equations, subscripts with f and g denote the order of their derivative with respect to x. a1(x), b1(x), c1(x) and d1(x) are obtained from boundary conditions (38) as

$$\begin{array}{c}{b}_{1}(x)=0,\,{d}_{1}(x)=0,\\ {a}_{1}(x)=\frac{-{h}^{2}}{3\varphi +h+\alpha {\delta }^{2}\varphi h{h}_{1}^{2}}[\begin{array}{c}3{h}^{2}\eta (7\varphi +h)+2\xi (5\varphi +h)+4{h}^{4}{\rm{\Omega }}(9\varphi +h)\\ +\alpha \varphi {\delta }^{2}h(3{h}^{2}\eta {\eta }_{1}^{2}+2\xi {h}_{1}^{2})+4\alpha \varphi {\delta }^{2}{\rm{\Omega }}{h}_{1}^{2}\end{array}]\\ {c}_{1}(x)=\frac{-1}{3\varphi +h+\alpha {\delta }^{2}\varphi h{h}_{1}^{2}}[\begin{array}{c}2{h}^{6}\eta (9\varphi +h)+{h}^{4}\xi (7\varphi +h)+3{h}^{8}{\rm{\Omega }}(11\varphi +h)\\ +\alpha \varphi {\delta }^{2}{h}^{5}(2{h}^{2}\eta {\eta }_{1}^{2}+\xi {h}_{1}^{2})+3\alpha \varphi {\rm{\Omega }}{h}^{9}{h}_{1}^{2}\end{array}]\end{array}$$
(45)

We can obtain the similar expressions for ψ2, ψ3 and so on. Since we aimed to find approximate analytical solution therefore, two term approximate solution using Eqs (39–45) can be written as

$$\psi ={\rm{\Omega }}{y}^{9}+\eta {y}^{7}+\xi {y}^{5}+m{y}^{3}+ny,$$
(46)

where

$$\begin{array}{c}m(x)=f(x)+{a}_{1}(x),\\ n(x)=g(x)+{c}_{1}(x)\end{array}$$
(47)

Velocity components can readily be obtained by using Eq. (46) into Eq. (18) as

$$\begin{array}{c}u=9{\rm{\Omega }}{y}^{8}+7\eta {y}^{6}+5\xi {y}^{4}+3m{y}^{2}+n,\\ v\,=\,-\,{{\rm{\Omega }}}_{1}{y}^{9}+{\eta }_{1}{y}^{7}+{\xi }_{1}{y}^{5}+{m}_{1}{y}^{3}+{n}_{1}y,\end{array}$$
(48)

where superscripts with Ω, η, ξ, m and n denote their first derivative with respect to x.

Pressure Distribution

Expression for pressure distribution can be obtained by integrating Eq. (11) as

$$\begin{array}{c}p(x,y)=\delta \frac{\delta u}{\delta x}+\frac{1}{\delta }\int (\frac{{\delta }^{2}u}{\delta {y}^{2}}-{H}^{2}u)dx-Re(\int u\frac{\delta u}{\delta x}dx+v\frac{\delta u}{\delta y}dx)\\ \,\,\,\,+{\rm{a}}\,{\rm{constant}}\,{\rm{of}}\,{\rm{itegration}}\end{array}$$
(49)

Mean presuure drop can be obtained by the formula

$$\bar{p}(x)={\int }_{0}^{h(x)}p(x,y)dy.$$
(50)

Thus mean pressure drop between x = 0 and x = x0 is denoted by

$${\rm{\Delta }}\bar{p}({x}_{0})=\bar{p}(0)-\bar{p}({x}_{0}).$$
(51)

Wall shear stress

For two-dimensional flow, wall shear stress in dimensional form is defined as

$$\tau {^{\prime} }_{w}=\frac{(\sigma {^{\prime} }_{y^{\prime} y^{\prime} }-\sigma {^{\prime} }_{x^{\prime} x^{\prime} })\frac{dh^{\prime} }{dx^{\prime} }+\sigma {^{\prime} }_{x^{\prime} y^{\prime} }[1-{(\frac{dh^{\prime} }{dx^{\prime} })}^{2}]}{1-{(\frac{dh^{\prime} }{dx^{\prime} })}^{2}}\,at\,y^{\prime} =h^{\prime} (x^{\prime} ),$$
(52)

where

$$\sigma {^{\prime} }_{x^{\prime} x^{\prime} }=2\mu \frac{\partial u^{\prime} }{\partial x^{\prime} },\,\sigma {^{\prime} }_{y^{\prime} y^{\prime} }=2\mu \frac{\partial v^{\prime} }{\partial x^{\prime} },\,\sigma {^{\prime} }_{x^{\prime} x^{\prime} }=\mu [\frac{\partial u^{\prime} }{\partial y^{\prime} }+\frac{\partial v^{\prime} }{\partial x^{\prime} }].$$
(53)

Using Eq. (9), we get shear stress in dimensionless form as

$${\tau }_{w}=\frac{2{\delta }^{2}(\frac{\partial v}{\partial y}-\frac{\partial u}{\partial x})\frac{dh}{dx}+(\frac{\partial u}{\partial y}+{\delta }^{2}\frac{\partial v}{\partial x})(1-{\delta }^{2}{(\frac{dh}{dx})}^{2})}{1-{\delta }^{2}{(\frac{dh}{dx})}^{2}}.$$
(54)

where

$${\tau }_{w}=({h}_{0}^{2}/\mu {Q}_{0})\tau {^{\prime} }_{w}.$$
(55)

Pressure Distribution

Expression for pressure distribution can be obtained by using Eqs (30), (18) and (11) as

$$\begin{array}{c}p(x,y)=\delta \frac{\partial u}{\partial x}+\frac{1}{\delta }\int (\frac{{\partial }^{2}u}{\partial {y}^{2}}-{H}^{2}u)dx-Re(\int u\frac{\partial u}{\partial x}dx+\int v\frac{\partial u}{\partial y}dx)\\ \,\,\,\,+{\rm{a}}\,{\rm{constan}}\,{\rm{to}}\,{\rm{fintegration}},\end{array}$$
(56)

Mean pressure drop can be obtained by the formula

$$\bar{p}(x)={\int }_{0}^{h(x)}p(x,y)dy.$$
(57)

Thus, mean pressure drop between x = 0 and x = x0 is obtained by

$${\rm{\Delta }}\bar{p}({x}_{0})=\bar{p}(0)-\bar{p}({x}_{0}).$$
(58)

Results and Discussion

This analysis is carried out to study the behavior of flow of viscous fluid through a non-uniform permeable channel under the influence of transverse magnetic field. The flux is accounted for by considering as an exponential function of downstream distance. It may be recalled that δ characterize the ratio of inlet half-width to the length of the channel, λ is the wavelength, m is the slope parameter and α, ϕ and H represent the reabsorption, slip and Hartmann number, respectively. The significant characteristics of pertinent parameters on velocity, pressure and shear stress are discussed through graphs. The moderate values of the parameters ε(=0.1), Re(=1) and δ(=0.1) from already existing literature on physiological problems20,25,35,36,37 are chosen in our analysis.

A comparison of present results is made with already published work35 in the limiting case of negligible magnetic strength (H → 0). For this purpose, numerical values of mean pressure drop over the length (x0 = 1) of the channel for different values of reabsorption parameter (α) and slip parameter (ϕ) are computed by software Mathematica38 and presented in Table 1. Our results are close to the published results35.

Table 1 Comparison of pressure drop over the length of the channel for limiting case when H → 0 and Re = 1, δ = 0.1 and ϕ = 0.1.
Full size table

The effects of various parameters on velocity components (u, v) and magnitude of wall shear stress (τw) are discussed by plotting graphs. Figures 2 and 3 portray the impact of reabsorption parameter (α) on the axial and transverse velocity profiles. It is witnessed that axial and normal velocity components are diminishing functions of α. This is natural because of loss of fluid from walls of the channel and decay of volume flow rate. It is worth mentioning here that the present phenomenon reduces to the case of impermeable walls when α → 0.

Figure 2
figure 2

Effect of reabsorption parameter (α) on axial velocity (u) at x = 0.3 when ϕ = 0.1, H = 2 and m = 0.1.

Full size image
Figure 3
figure 3

Effect of reabsorption parameter (α) on transverse velocity (v) at x = 0.3 when ϕ = 0.1, H = 2 and m = 0.1.

Full size image

The effect of slip parameter ϕ on axial and transverse velocity is depicted by Figs 4 and 5. It is noteworthy here that ϕ ≠ 0 corresponds to no slip condition and ϕ = 0 represents velocity slip at the channel wall. It is noticed that axial velocity u shows a decreasing trend near the center and increasing trend near the wall of the channel. This cut off is observed at y = 0.6 for particular choice of ϕ. This observation is somewhat intriguing and must be discussed by some physical reasoning. As expected axial velocity u becomes zero at the wall of the channel for ϕ = 0. However there is an increase in u for ϕ ≠ 0 due to the fact that slip occurs at the wall. Since u is proportional to the slip parameter ϕ at the wall therefore, by increasing ϕ, u also increases near the wall. Therefore, for ϕ = 0=, u goes to zero at the boundary and thus crossover of u for ϕ = 0.1, ϕ = 0.3 and ϕ = 0.5 is approximately y = 0.6. Moreover, Fig. 5 shows that v is a decreasing function of ϕ As suggested by Kohler37, reasonable values of ϕ are upto 0.5.

Figure 4
figure 4

Effect of slip parameter (ϕ) on axial velocity (u) at x = 0.3 when α = 1, H = 2 and m = 0.1.

Full size image
Figure 5
figure 5

Effect of slip parameter (ϕ) on transverse velocity (v) at x = 0.3 when α = 1, H = 2 and m = 0.1.

Full size image

Figures 6 and 7 depict the axial and transverse components of velocity field for different values of Hartmann number (H). It is observed from Fig. 6 that u decreases upto half of the channel and beyond that it increases. This effect of H on u near the wall is opposite to the effect of H in case of impermeable channel flow where u is damped by the application of transverse magnetic field. Physically, rising the parameter H produces the Lorentz force. This is a resistive force which suppress the velocity field. This implies that magnetic field strength can be utilized to control the velocity field and hence its application may be important from physiological point of view. It is interesting to note here that present results reduce to the already exist results for H = 035. The axial and transverse components of velocity are plotted vs y-axis for different values of slope parameter m in Figs 8 and 9. It is observed that u has a higher value for divergent channel than a normal or convergent channel near the wall of the channel. Transverse velocity v also has higher values for divergent channel than a normal or convergent channel. From Figs 10 and 11, it is noticed that u and v are diminishing functions of downstream distance. This is due to the fact that reabsorption occurs at the walls of the channel which results in reduction of flux with axial distance.

Figure 6
figure 6

Effect of Hartmann number (H) on axial velocity (u) at x = 0.3 when α = 1, ϕ = 0.1 and m = 0.1.

Full size image
Figure 7
figure 7

Effect of Hartmann number (H) on transverse velocity (v) at x = 0.3 when α = 1, ϕ = 0.1 and m = 0.1.

Full size image
Figure 8
figure 8

Effect of slope parameter (m) on axial velocity (u) at x = 0.3 when α = 1, ϕ = 0.1 and H = 2.

Full size image
Figure 9
figure 9

Effect of slope parameter (m) on transverse velocity (v) at x = 0.3 when α = 1, ϕ = 0.1 and H = 2.

Full size image
Figure 10
figure 10

Effect of axial distance (x) on axial velocity (u) when α = 1, ϕ = 0.1 and H = 2.

Full size image
Figure 11
figure 11

Effect of axial distance (x) on transverse velocity (v) when α = 1, ϕ = 0.1 and H = 2.

Full size image

Figures 12–17 exhibit the distribution of the magnitude of wall shear stress τw with x for different values of α, ϕ, m and H. The magnitude of τw is observed as decreasing function of α, ϕ and m however it is in increasing function of H. It is worth mentioning here that τw increases by increasing H for all the cases of convergent, divergent or normal channel.

Figure 12
figure 12

Effect of reabsorption parameter (α) on wall shear stress (τw) when ϕ = 0.1, H = 2 and m = 0.1.

Full size image
Figure 13
figure 13

Effect of slip parameter (ϕ) on wall shear stress (τw) when α = 1, H = 2 and m = 0.1.

Full size image
Figure 14
figure 14

Effect of slope parameter (m) on wall shear stress (τw) when α = 1, ϕ = 0.1 and H = 2.

Full size image
Figure 15
figure 15

Effect of Hartmann number (H) on wall shear stress (τw) in a convergent channel when ϕ = 0.1 and α = 1.

Full size image
Figure 16
figure 16

Effect of Hartmann number (H) on wall shear stress (τw) in a normal channel when ϕ = 0.1 and α = 1.

Full size image
Figure 17
figure 17

Effect of Hartmann number (H) on wall shear stress (τw) in a divergent channel when ϕ = 0.1 and α = 1.

Full size image

Conclusions

In this paper, the problem of MHD slip flow of a viscous fluid through a non-uniform channel under the influence of transverse magnetic field is discussed. Volume flow rate is assumed to be a function of downstream distance. Following conclusions are made from this study

  • The values of u and τw decrease with α while the value of v increases with α.

  • v and τw decrease by increasing ϕ. However, u decreases in a region near the center of the channel and inverse is seen near the wall for higher values of ϕ.

  • By increasing Hartmann number (H), u and v decrease in a region near the center and increase near the wall. Thus velocity field can be controlled by applying appropriate magnetic field.

  • τw increases by increasing H.

  • Magnitude of wall shear stress τw decreases for a divergent channel in comparison with a convergent channel. v and u have higher values for a divergent channel.

  • All the flow variables decrease with downstream distance. This physically obvious due to loss of fluid from the wall.

  • Limiting case of this study i.e., fo r H → 0, results are compared with those of Muthu35.

Hoping that this study would provide a useful information in improving the already available models for investigating different biophysical and engineering problems. Proper knowledge of flow situations when a magnetic field is being applied on flow in a non-uniform channel may become useful in magnetic or electromagnetic therapy as well as in many engineering problems.