Introduction

Quantum computers provide the possibility of solving certain computational tasks much faster than any classical counterpart using the best currently known algorithms1,2,3,4,5, thus a great deal of effort has been devoted to building scalable and functional quantum computers over the last two decades. Solving a quantum computational task corresponds to performing a unitary transformation on the quantum register, which is composed of multiple qubits. Any quantum algorithm can be decomposed into a sequence of single-qubit rotations and entangling two-qubit logical gates, which form a universal set of quantum operations6,7. Moreover, various kinds of physical realizations of quantum computations have been intensively studied8,9,10,11,12,13,14,15. However, if only single-qubit and two-qubit gates are available, the qubits scale up so that the approach becomes very complicated and it may be hard to implement. On the other hand, using gates acting on more than two qubits can significantly simplify the decomposition of otherwise intractable algorithms£¬ which can shorten the operation time and promise higher fidelity. Therefore multiqubit gates play a central role in quantum algorithms, quantum corrections, and quantum networks, and they serve as a stepping stone towards the realization of a scalable quantum computer.

Among the multiqubit gates, the quantum Toffoli gate (controlled-controlled-NOT gate)16 is one typical three-qubit gate. It flips the state of a target qubit conditioned on the state of two control qubits. This gate plus a Hadamard gate can form a universal set of gates in quantum computation. Moreover, it can be directly used to implement the complex quantum algorithms1 and quantum simulation17,18,19, and has immediate practical applications as correcting operation in quantum error correction schemes20,21,22,23,24. Therefore, the Toffoli gate is vitally important for quantum computing, and improving the design of the Toffoli gate can make the implementation of large-scale quantum computation more tractable. So far, the minimum cost for implementing a three-qubit Toffoli gate is five two-qubit gates25, and the decomposition of a generalized n-qubit Toffoli gate involves O(n2) two-qubit gates7. In experiment the Toffoli gate has been first implemented in nuclear magnetic resonance20. Recently, the three-qubit quantum Toffoli gate has been achieved in some other physical architectures, such as linear optics, ion-trap qubits, superconducting circuits, quantum dots (QDs), and diamond nitrogen-vacancy (NV) defect centres26,27,28,29,30,31,32. In these experiments based on the idea of “hiding” states, the required resources are greatly reduced in contrast with theoretical proposals, which use only two-level systems. However, they still require three two-qubit or qubit-qutrit gates so that the fidelity would be significantly deteriorated by decoherence. Therefore, it is important to implement the quantum Toffoli gate in one-step without using any two-qubit or qubit-qutrit gate.

In this work, we propose an efficient scheme to realize a Toffoli gate in one-step with a coupled-cavity model. The matrix form of the three-qubit Toffoli gate expanded in the basis {|0〉1, |1〉1, |0〉2, |1〉2, |0〉3, |1〉3} is

$${U}_{{\rm{toff}}}=(\begin{array}{llllllll}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\end{array}),$$
(1)

where the target qubit swaps its information \(\mathrm{|0}{\rangle }_{3}\iff \mathrm{|1}{\rangle }_{3}\) if and only if two control qubits are in |01〉12. Note that it is equivalent to the standard form of a Toffoli gate upon a local unitary transformation. Coupled cavity arrays describes a series of optical cavities, each of which contains one or more qubits or atoms, and photons can hop between two neighboring cavities. This model can overcome the problem of individual addressability and has emerged as a fascinating alternative for simulating quantum many-body phenomena. Theoretical works on quantum information processing and quantum computing have been proposed with using the atom-cavity interaction in coupled cavity arrays33,34,35,36,37,38,39,40,41. The merit of our scheme is that the Toffoli gate is implemented in one-step without any single-qubit or two-qubit operation, which can significantly simplify the experimental realization and shorten the operation time. Meanwhile, it is easy to control and measure qubit separately because there is one three-level atom in each cavity. Furthermore, we encode the quantum information into the low-lying states of three identical atoms without any ancillary level compared with ref.42.

Results

In Fig. 1 we consider three coupled cavities with one three-level atom in each cavity. The k-th (k = 1, 2, 3) atom has two ground states |0 k 〉 and |1 k 〉 and one excited state |e k 〉 with energies ω a , ω b and ω e , respectively. Each \({\mathrm{|0}}_{k}\rangle \leftrightarrow |{e}_{k}\rangle \) transition is coupled to its corresponding cavity mode with the coupling strength g k , detuned by Δ. Meanwhile, the transitions \({\mathrm{|0}}_{3}\rangle \leftrightarrow |{e}_{3}\rangle \) and \({\mathrm{|1}}_{3}\rangle \leftrightarrow |{e}_{3}\rangle \) for the target atom are driven by a pair of classical fields with the Rabi frequencies Ω a and Ω b respectively, detuned by the same parameter Δ. In addition, the cavities are coupled via the exchange of photons with the coupling constant J. The system Hamiltonian takes the following form (ħ = 1)

$$H={H}_{{\rm{cla}}}+{H}_{{\rm{int}}}+{H}_{{\rm{hop}}}+{H}_{{\rm{free}}},$$
(2)

where

$$\begin{array}{rcl}{H}_{{\rm{cla}}} & = & {{\rm{\Omega }}}_{a}(|{e}_{3}\rangle \langle {0}_{3}|{e}^{-i{\omega }_{{l}_{1}}t}+{\mathrm{|0}}_{3}\rangle \langle {e}_{3}|{e}^{i{\omega }_{{l}_{1}}t})\\ & & +{{\rm{\Omega }}}_{b}(|{e}_{3}\rangle \langle {1}_{3}|{e}^{-i{\omega }_{{l}_{2}}t}+{\mathrm{|1}}_{3}\rangle \langle {e}_{3}|{e}^{i{\omega }_{{l}_{2}}t}),\\ {H}_{{\rm{int}}} & = & \sum _{k=1}^{3}\,{g}_{k}({a}_{k}|{e}_{k}\rangle \langle {0}_{k}|+{a}_{k}^{\dagger }{\mathrm{|0}}_{k}\rangle \langle {e}_{k}|),\\ {H}_{{\rm{hop}}} & = & \sum _{j=1}^{2}\,J({a}_{j}^{\dagger }{a}_{j+1}+{a}_{j}{a}_{j+1}^{\dagger }),\\ {H}_{{\rm{free}}} & = & \sum _{k=1}^{3}\,({\omega }_{e}|{e}_{k}\rangle \langle {e}_{k}|+{\omega }_{a}{\mathrm{|0}}_{k}\rangle \langle {0}_{k}|+{\omega }_{b}{\mathrm{|1}}_{k}\rangle \langle {1}_{k}|)+\sum _{k=1}^{3}\,{\omega }_{c}{a}_{k}^{\dagger }{a}_{k},\end{array}$$
(3)

where \({a}_{j}({a}_{j}^{\dagger })\) is the annihilation (creation) operator of the j-th cavity mode, \({\omega }_{{l}_{1}}\) and \({\omega }_{{l}_{2}}\) are the frequencies of two classical fields, and ω c is the frequency of the cavity. By changing to the interaction picture, and performing a rotation with the frame defined by \(U=\exp (i{\rm{\Delta }}t\,{\sum }_{i=1}^{3}\,|{e}_{i}\rangle \langle {e}_{i}|)\), the Hamiltonian can be written as

$$\begin{array}{rcl}{H}_{I} & = & {{\rm{\Omega }}}_{a}(|{e}_{3}\rangle \langle {0}_{3}|+{\mathrm{|0}}_{3}\rangle \langle {e}_{3}|)+{{\rm{\Omega }}}_{b}(|{e}_{3}\rangle \langle {1}_{3}|+{\mathrm{|1}}_{3}\rangle \langle {e}_{3}|)\\ & & +\sum _{k=1}^{3}\,{g}_{k}({a}_{k}|{e}_{k}\rangle \langle {0}_{k}|+{a}_{k}^{\dagger }{\mathrm{|0}}_{k}\rangle \langle {e}_{k}|)\\ & & +\sum _{j=1}^{2}\,J({a}_{j}^{\dagger }{a}_{j+1}+{a}_{j}{a}_{j+1}^{\dagger })+\sum _{k=1}^{3}\,{\rm{\Delta }}|{e}_{k}\rangle \langle {e}_{k}|,\end{array}$$
(4)

where we have assumed g k  = g for simplicity.

Figure 1
figure 1

Three coupled cavities with one three-level atom in each cavity are shown for simulating the Toffoli gate. From left to right the atoms are labeled as 1, 2, 3. We consider the first two atoms as the control qubits while the third atom is the target qubit. The two ground state levels |0 i 〉 and |1 i 〉 (i = 1, 2, 3) of each atom define a single qubit.

Full size image

In the following, we will discuss the scheme to implement the Toffoli gate based on the large detuning case. Here we consider that the two classical optical pumping lasers are both sufficiently weak (i.e. the Rabi frequencies Ω a and Ω b are both very small compared with {J, g, Δ}), and the excited states of the atoms and the excited cavity field modes are not initially populated, the highly excited level can be neglected33,34,35,43,44. Based on the interaction form of the Hamiltonian (4), the qubit basis {|0〉1, |1〉1, |0〉2, |1〉2, |0〉3, |1〉3} a with cavities in vacuum states can be divided into four subspaces. For the first subspace {|010〉 a  |000〉 c , |011〉 a  |000〉 c , |e10〉 a  |000〉 c , |01e〉 a  |000〉 c , |010〉 a  |100〉 c , |010〉 a  |010〉 c , |010〉 a  |001〉 c }, we first diagonalize the strong interaction described by atom-cavity Hamiltonian in Eq. (4). Based on the new basis \(\{|{{\rm{\Phi }}}_{1}^{\mathrm{(1)}}\rangle \), \(|{{\rm{\Phi }}}_{2}^{\mathrm{(1)}}\rangle \), \(|{{\rm{\Phi }}}_{a}^{\mathrm{(1)}}\rangle \), \(|{{\rm{\Phi }}}_{b}^{\mathrm{(1)}}\rangle \), \(|{{\rm{\Phi }}}_{3}^{\mathrm{(1)}}\rangle \}\) with

$$\begin{array}{rcl}|{{\rm{\Phi }}}_{1}^{\mathrm{(1)}}\rangle & = & \frac{1}{2}\mathrm{|010}{\rangle }_{a}{(\mathrm{|100}\rangle -\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{2}^{\mathrm{(1)}}\rangle & = & \frac{1}{2}\mathrm{|010}{\rangle }_{a}{(\mathrm{|100}\rangle +\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{3}^{\mathrm{(1)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{|010}{\rangle }_{a}\mathrm{(|100}\rangle -\mathrm{|001}\rangle {)}_{c},\\ |{{\rm{\Phi }}}_{a}^{\mathrm{(1)}}\rangle & = & \frac{1}{\sqrt{2}}(|e10\rangle +\mathrm{|01}e\rangle {)}_{a}\mathrm{|000}{\rangle }_{c},\\ |{{\rm{\Phi }}}_{b}^{\mathrm{(1)}}\rangle & = & \frac{1}{\sqrt{2}}(|e10\rangle -\mathrm{|01}e\rangle {)}_{a}\mathrm{|000}{\rangle }_{c},\end{array}$$
(5)

the atom-cavity Hamiltonian reads:

$${T}_{1}=(\begin{array}{ccccc}-\sqrt{2}J & 0 & \frac{g}{\sqrt{2}} & 0 & 0\\ 0 & \sqrt{2}J & \frac{g}{\sqrt{2}} & 0 & 0\\ \frac{g}{\sqrt{2}} & \frac{g}{\sqrt{2}} & {\rm{\Delta }} & 0 & 0\\ 0 & 0 & 0 & {\rm{\Delta }} & g\\ 0 & 0 & 0 & g & 0\end{array}).$$
(6)

The effective Hamiltonian in the first subspace can be evaluated explicitly (see Methods)

$$\begin{array}{rcl}{H}_{{\rm{eff}}}^{1} & = & -\frac{{{\rm{\Omega }}}_{a}^{2}}{2{\rm{\Delta }}}\mathrm{|010}\rangle \langle \mathrm{010|}-\frac{{{\rm{\Omega }}}_{b}^{2}}{2{\rm{\Delta }}}\mathrm{|011}\rangle \langle \mathrm{011|}\\ & & -\frac{{{\rm{\Omega }}}_{a}{{\rm{\Omega }}}_{b}}{2{\rm{\Delta }}}\mathrm{(|011}\rangle \langle \mathrm{010|}+\mathrm{|010}\rangle \langle \mathrm{011|)}.\end{array}$$
(7)

Similar to the analysis of the first subspace, we consider the second subspace {|000〉 a  |000〉 c , |001〉 a  |000〉 c , |e00〉 a  |000〉 c , |0e0〉 a  |000〉 c , |00e〉 a  |100〉 c , |000〉 a  |100〉 c , |000〉 a  |010〉 c , |000〉 a  |001〉 c }. Based on the new basis \(\{|{{\rm{\Phi }}}_{1}^{\mathrm{(2)}}\rangle \), \(|{{\rm{\Phi }}}_{a}^{\mathrm{(2)}}\rangle \), \(|{{\rm{\Phi }}}_{2}^{\mathrm{(2)}}\rangle \), \(|{{\rm{\Phi }}}_{b}^{\mathrm{(2)}}\rangle \), \(|{{\rm{\Phi }}}_{3}^{\mathrm{(2)}}\rangle \), \(|{{\rm{\Phi }}}_{c}^{\mathrm{(2)}}\rangle \}\) with

$$\begin{array}{rcl}|{{\rm{\Phi }}}_{1}^{\mathrm{(2)}}\rangle & = & \frac{1}{2}\mathrm{|000}{\rangle }_{a}{(\mathrm{|100}\rangle -\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{2}^{\mathrm{(2)}}\rangle & = & \frac{1}{2}\mathrm{|000}{\rangle }_{a}{(\mathrm{|100}\rangle +\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{3}^{\mathrm{(2)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{|000}{\rangle }_{a}\mathrm{(|100}\rangle -\mathrm{|001}\rangle {)}_{c},\\ |{{\rm{\Phi }}}_{a}^{\mathrm{(2)}}\rangle & = & \frac{1}{2}{(|e00\rangle -\sqrt{2}\mathrm{|0}e0\rangle +\mathrm{|00}e\rangle )}_{a}\mathrm{|000}{\rangle }_{c},\\ |{{\rm{\Phi }}}_{b}^{\mathrm{(2)}}\rangle & = & \frac{1}{2}{(|e00\rangle +\sqrt{2}\mathrm{|0}e0\rangle +\mathrm{|00}e\rangle )}_{a}\mathrm{|000}{\rangle }_{c},\\ |{{\rm{\Phi }}}_{c}^{\mathrm{(2)}}\rangle & = & \frac{1}{\sqrt{2}}(|e00\rangle -\mathrm{|00}e\rangle {)}_{a}\mathrm{|000}{\rangle }_{c},\end{array}$$
(8)

the atom-cavity Hamiltonian reads:

$${T}_{2}=(\begin{array}{cccccc}-\sqrt{2}J & g & 0 & 0 & 0 & 0\\ g & {\rm{\Delta }} & 0 & 0 & 0 & 0\\ 0 & 0 & \sqrt{2}J & g & 0 & 0\\ 0 & 0 & g & {\rm{\Delta }} & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & g\\ 0 & 0 & 0 & 0 & g & {\rm{\Delta }}\end{array}).$$
(9)

The effective Hamiltonian in the second subspace reduces to (see Methods)

$$\begin{array}{rcl}{H}_{{\rm{eff}}}^{2} & = & \frac{1}{\frac{{g}^{4}}{{J}^{2}{\rm{\Delta }}}-2{\rm{\Delta }}}[{{\rm{\Omega }}}_{a}^{2}\mathrm{|000}\rangle \langle \mathrm{000|}+{{\rm{\Omega }}}_{b}^{2}\mathrm{|001}\rangle \langle \mathrm{001|}\\ & & +{{\rm{\Omega }}}_{a}{{\rm{\Omega }}}_{b}\mathrm{(|000}\rangle \langle \mathrm{001|}+\mathrm{|100}\rangle \langle \mathrm{000|)]}.\end{array}$$
(10)

Based on the above condition \(\{|{{\rm{\Omega }}}_{a}|,|{{\rm{\Omega }}}_{b}|\}\ll \{J,g,{\rm{\Delta }}\}\) and \(J\ll g\), this effective Hamiltonian is \({H}_{{\rm{eff}}}^{2}\approx 0\), which means that the qubit states |000〉 and |001〉 remain unchanged during the whole evolution time.

For the third subspace {|100〉 a  |000〉 c , |101〉 a  |000〉 c , |1e0〉 a  |000〉 c , |10e〉 a  |000〉 c , |100〉 a  |100〉 c , |100〉 a  |010〉 c , |100〉 a  |001〉 c }, based on the new basis \(\{|{{\rm{\Phi }}}_{1}^{\mathrm{(3)}}\rangle \), \(|{{\rm{\Phi }}}_{2}^{\mathrm{(3)}}\rangle \), \(|{{\rm{\Phi }}}_{3}^{\mathrm{(3)}}\rangle \), \(|{{\rm{\Phi }}}_{a}^{\mathrm{(3)}}\rangle \), \(|{{\rm{\Phi }}}_{b}^{\mathrm{(3)}}\rangle \}\) with

$$\begin{array}{rcl}|{{\rm{\Phi }}}_{1}^{\mathrm{(3)}}\rangle & = & \frac{1}{2}\mathrm{|100}{\rangle }_{a}{(\mathrm{|100}\rangle -\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{2}^{\mathrm{(3)}}\rangle & = & \frac{1}{2}\mathrm{|100}{\rangle }_{a}{(\mathrm{|100}\rangle +\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{3}^{\mathrm{(3)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{|100}{\rangle }_{a}\mathrm{(|100}\rangle -\mathrm{|001}\rangle {)}_{c},\\ |{{\rm{\Phi }}}_{a}^{\mathrm{(3)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{(|1}e0\rangle +\mathrm{|10}e\rangle {)}_{a}\mathrm{|000}{\rangle }_{c},\\ |{{\rm{\Phi }}}_{b}^{\mathrm{(3)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{(|1}e0\rangle -\mathrm{|10}e\rangle {)}_{a}\mathrm{|000}{\rangle }_{c},\end{array}$$
(11)

the atom-cavity Hamiltonian is given by:

$${T}_{3}=(\begin{array}{ccccc}-\sqrt{2}J & 0 & 0 & -\frac{2-\sqrt{2}}{4}g & -\frac{2+\sqrt{2}}{4}g\\ 0 & \sqrt{2}J & 0 & \frac{2+\sqrt{2}}{4}g & \frac{2-\sqrt{2}}{4}g\\ 0 & 0 & 0 & -\frac{g}{2} & \frac{g}{2}\\ -\frac{2-\sqrt{2}}{4}g & \frac{2+\sqrt{2}}{4}g & -\frac{g}{2} & {\rm{\Delta }} & 0\\ -\frac{2+\sqrt{2}}{4}g & \frac{2-\sqrt{2}}{4}g & \frac{g}{2} & 0 & {\rm{\Delta }}\end{array}).$$
(12)

The effective Hamiltonian in the third subspace is (see Methods)

$${H}_{{\rm{eff}}}^{3}=0,$$
(13)

which means that the qubit states |100〉 and |101〉 remain unchanged during the whole evolution time.

For the fourth subspace {|110〉 a  |000〉 c , |111〉 a  |000〉 c , |11e〉 a  |000〉 c , |110〉 a  |100〉 c , |110〉 a  |010〉 c , |110〉 a  |001〉 c }, based on the new basis \(\{|{{\rm{\Phi }}}_{1}^{\mathrm{(4)}}\rangle \), \(|{{\rm{\Phi }}}_{2}^{\mathrm{(4)}}\rangle \), \(|{{\rm{\Phi }}}_{3}^{\mathrm{(4)}}\rangle \), \(|{{\rm{\Phi }}}_{a}^{\mathrm{(4)}}\rangle \}\) with

$$\begin{array}{rcl}|{{\rm{\Phi }}}_{1}^{\mathrm{(4)}}\rangle & = & \frac{1}{2}\mathrm{|110}{\rangle }_{a}{(\mathrm{|100}\rangle -\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{2}^{\mathrm{(4)}}\rangle & = & \frac{1}{2}\mathrm{|110}{\rangle }_{a}{(\mathrm{|100}\rangle +\sqrt{2}\mathrm{|010}\rangle +\mathrm{|001}\rangle )}_{c},\\ |{{\rm{\Phi }}}_{3}^{\mathrm{(4)}}\rangle & = & \frac{1}{\sqrt{2}}\mathrm{|110}{\rangle }_{a}\mathrm{(|100}\rangle -\mathrm{|001}\rangle {)}_{c},\\ |{{\rm{\Phi }}}_{a}^{\mathrm{(4)}}\rangle & = & \mathrm{|11}e{\rangle }_{a}\mathrm{|000}{\rangle }_{c},\end{array}$$
(14)

the atom-cavity Hamiltonian reads:

$${T}_{4}=(\begin{array}{cccc}-\sqrt{2}J & 0 & 0 & \frac{g}{2}\\ 0 & \sqrt{2}J & 0 & \frac{g}{2}\\ 0 & 0 & 0 & -\frac{g}{\sqrt{2}}\\ \frac{g}{2} & \frac{g}{2} & -\frac{g}{\sqrt{2}} & {\rm{\Delta }}\end{array}).$$
(15)

The effective Hamiltonian in the fourth subspace is (see Methods)

$${H}_{{\rm{eff}}}^{4}=\mathrm{0,}$$
(16)

which means that the qubit states |110〉 and |111〉 remain unchanged during the whole evolution time. Thus the time evolution operator for the final effective Hamiltonian can be written as

$$\begin{array}{rcl}U(t) & = & \frac{1}{2}\mathrm{(1}-\exp (imt))\,\mathrm{(|010}\rangle \langle \mathrm{011|}+\mathrm{|011}\rangle \langle \mathrm{010|)}\\ & & +\frac{1}{2}\mathrm{(1}+\exp (imt))\,\mathrm{(|010}\rangle \langle \mathrm{010|}+\mathrm{|011}\rangle \langle \mathrm{011|),}\end{array}$$
(17)

where m = Ω2/Δ with the parameters Ω b  = −Ω a  = Ω. Adjust the evolution period T = πΔ/Ω2, we obtain the three-qubit Toffoli gate which takes the form of Eq. (1).

In what follows, we check the accuracy of the effective Hamiltonian compared to the original Hamiltonian with the populations of three qubit states {|000〉, |001〉, |010〉, |011〉, |100〉, |101〉, |110〉, |111〉} a  |000〉 c . In Fig. 2, (a) plots the conversion of states |010〉 a  |000〉 c and |011〉 a  |000〉 c when the system reserves the single excitation. The population can achieve 0.9981 at the period time. (b) depicts the populations of states |000〉 a  |000〉 c , |001〉 a  |000〉 c , |100〉 a  |000〉 c , |101〉 a  |000〉 c , |110〉 a  |000〉 c and |111〉 a  |000〉 c for the system reserving the single excitation. The minimum data of the population is 0.9938 during the evolution time. Since the system do not conserve the total number of excitations, and in front we neglect the highly excited level under the weak excitation case, here we further consider the numerical simulation for the system reserving the double excitation in (c) and (d). Compare plots (c) with (a), (d) with (b), it is found that the results for the double excitation case are in accord with the results for the single excitation case. These numerical results reveal that the effective Hamiltonian is excellently close to the original Hamiltonian under the given parameters. To make our results more clearly, Fig. 3 gives the truth table of the Toffoli gate at the period time for the single excitation case. The fidelity for the Toffoli gate in the ideal case is \(F(T)=\frac{1}{8}|{\rm{tr}}[{U}^{\dagger }(T){U}_{{\rm{Toffoli}}}]|=0.9991\), with U(T) being the final evolution operator based on the original Hamiltonian (4) and UToffoli being the ideal Toffoli gate. Thus a Toffoli gate is implemented with high fidelity. Furthermore, we numerically discuss the case that the atom-cavity coupling strengths g1, g2 and g3 are different with g1 = g + δ, g2 = g − δ and g3 = g, the Toffili gate can be implemented as well, as shown in Fig. 4. When the parameter δ ≤ 0.2, the fidelity contains higher than 95%.

Figure 2
figure 2

The populations of three qubit states when the system reserves the single excitation (a,b) and the double excitation (c,d), respectively. (a,c) Plot the populations conversion of states |010〉 and |011〉; (b,d) Plot the populations of states |000〉, |001〉, |100〉, |101〉, |110〉 and |111〉. The excited cavity field modes can be adiabatically eliminated. Choose the parameters as Ω b  = −Ω a  = Ω = 0.02g, Δ = g and J = 0.1g.

Full size image
Figure 3
figure 3

The truth table of the population of the Toffoli gate at the period time for the single excitation case. The parameters are chosen as Ω b  = −Ω a  = Ω = 0.02g, Δ = g and J = 0.1g.

Full size image
Figure 4
figure 4

The fidelity F of the Toffoli gate versus the parameter δ/g. The atom-cavity coupling constants g1 = g + δ, g2 = g − δ and g3 = g. The parameters are chosen as Ω b  = −Ω a  = Ω = 0.02g, Δ = g and J = 0.1g.

Full size image

Discussion

In the coupled-cavity arrays, the main decoherence effects in our scheme are the decay of cavities and the spontaneous emission of atoms. In this section, we numerically show how the decay of cavities and the spontaneous emission of atoms affect the fidelity of the resulting gate. The master equation for the whole system in the Markov approximation is governed by the following Lindblad equation45:

$$\begin{array}{rcl}\dot{\rho } & = & -i[{H}_{I},\rho ]+\sum _{j=1}^{3}\,\kappa ({a}_{j}\rho {a}_{j}^{\dagger }-\frac{1}{2}{a}_{j}^{\dagger }{a}_{j}\rho -\frac{1}{2}\rho {a}_{j}^{\dagger }{a}_{j})\\ & & +\sum _{l=\mathrm{0,1}}\,\sum _{j=1}^{3}\,{\gamma }_{j}^{el}({\sigma }_{le}^{j}\rho {\sigma }_{el}^{j}-\frac{1}{2}{\sigma }_{ee}^{j}\rho -\frac{1}{2}\rho {\sigma }_{ee}^{j}),\end{array}$$
(18)

where κ represents the cavity decay rate, \({\gamma }_{j}^{el}\) denotes the spontaneous emission rate of atoms from the level |e〉 j to |l〉 j for the j-th atom (j = 1, 2, 3) and we assume \({\gamma }_{j}^{e0}={\gamma }_{j}^{e1}=\gamma /2\) for convenience. To quantify the robustness of our logical gate, we adopt the gate fidelity defined as the Bures-Uhlmann fidelity

$$F({\rho }_{id},\rho (t))\equiv {\rm{Tr}}\sqrt{{\rho }_{id}^{\frac{1}{2}}\rho (t){\rho }_{id}^{\frac{1}{2}}},$$
(19)

where ρ(t) is the mixed output system state (obtained from the joint system-bath evolution after a partial trace over the bath) and ρ id is the density operator for target state. Here we choose the initial state as \(|{\rm{\Psi }}\rangle =\tfrac{1}{\sqrt{8}}\mathrm{(|000}\rangle +\mathrm{|001}\rangle +\mathrm{|010}\rangle -\mathrm{|011}\rangle +\mathrm{|100}\rangle +\mathrm{|101}\rangle +\mathrm{|110}\rangle +\mathrm{|111}\rangle {)}_{a}\mathrm{|000}{\rangle }_{c}\). The corresponding density operator for target state is \({\rho }_{id}=|{\rm{\Psi }}^{\prime} \rangle \langle {\rm{\Psi }}^{\prime} |\), with the target state \(|{\rm{\Psi }}^{\prime} \rangle =\tfrac{1}{\sqrt{8}}(|000\rangle +|001\rangle -|010\rangle +|011\rangle +\)\(|100\rangle +|101\rangle +|110\rangle +|111\rangle {)}_{a}|000{\rangle }_{c}\).

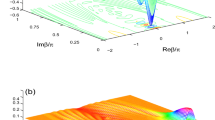
In Fig. 5 we depict the fidelity F of the Toffoli gate for the large detuning model as a function of the decoherence parameter κ/g and interaction time t/T. The fidelity F remains higher than 91%, which shows the Toffoli gate is robust against decoherence. Recently, the coupled cavity arrays can be constructed in several kinds of physical systems, such as photonic crystal defects46, toroidal microcavity arrays47, and superconducting stripline resonators48. Ref.47 investigated the suitability of toroidal microcavities for strong-coupling cavity quantum electrodynamics with the parameters \(g\sim 2\pi \times 750\) MHz, \(\gamma \sim 2\pi \times 2.62\) MHz, \(\kappa \sim 2\pi \times 3.5\) MHz. And ref.49 has shown the large-scale ultrahigh-Q coupled nanocavity arrays based on photonic crystals corresponding to the parameters \(g\sim 2.5\times {10}^{9}\) Hz, \(\gamma \sim 1.6\times {10}^{7}\) Hz, \(\kappa \sim 4\times {10}^{5}\) Hz. The fidelity of the Toffoli gate can achieve 95.43% and 98.14% for the above two different kinds of parameters (g, γ, κ), respectively. In the multi-qubit quantum computing networks the fidelities are relatively high.

Figure 5
figure 5

The fidelity F of the Toffoli gate versus the decoherence parameter κ/g and interaction time t/T, where γ = κ. The parameters are chosen as Ω b  = −Ω a  = Ω = 0.035g, Δ = g and J = 0.2g.

Full size image

In summary, we have proposed an efficient method to implement the Toffoli gate using an array of coupled cavities with one three-level atom in each cavity. The large detuning between atoms and classical (quantum) fields plays an important role. The Toffoli gate is implemented in one-step without any single-qubit or two-qubit operation, which can significantly simplify the experimental realization and shorten the operation time. Meanwhile, it is easy to control and measure qubit separately because there is one three-level atom in each cavity. Furthermore, we encode the quantum information into the low-lying states of three identical atoms without any ancillary level.

Methods

The effective Hamiltonian in the first subspace

In the case that the two classical optical pumping lasers are both sufficiently weak (i.e. the Rabi frequencies Ω a and Ω b are both very small compared with {J, g, Δ}), and the excited states are not initially populated, the excited states of the atoms and the excited cavity field modes can be adiabatically eliminated. The resulting effective dynamics will describe three two-level systems. To second order in perturbation theory, the dynamics are then given by the effective operators44:

$${H}_{{\rm{eff}}}=-\,\frac{1}{2}[{V}_{-}{H}_{NH}^{-1}{V}_{+}+{V}_{-}{({H}_{NH}^{-1})}^{\dagger }{V}_{+}],$$
(20)

here H NH  = T1, \({V}_{+}={{\rm{\Omega }}}_{a}|{e}_{3}\rangle \langle {0}_{3}|+{{\rm{\Omega }}}_{b}|{e}_{3}\rangle \langle {1}_{3}|\), and \({V}_{-}={V}_{+}^{\dagger }\). Applying the above equations to our setup, we first give the inverse matrix of T1

$${T}_{1}^{-1}=(\begin{array}{ccccc}\frac{{g}^{2}-2\sqrt{2}J{\rm{\Delta }}}{4{J}^{2}{\rm{\Delta }}} & -\frac{{g}^{2}}{4{J}^{2}{\rm{\Delta }}} & \frac{g}{2J\Delta } & 0 & 0\\ -\frac{{g}^{2}}{4{J}^{2}{\rm{\Delta }}} & \frac{{g}^{2}+2\sqrt{2}J{\rm{\Delta }}}{4{J}^{2}{\rm{\Delta }}} & -\frac{g}{2J{\rm{\Delta }}} & 0 & 0\\ \frac{g}{2J{\rm{\Delta }}} & -\frac{g}{2J{\rm{\Delta }}} & \frac{1}{{\rm{\Delta }}} & 0 & 0\\ 0 & 0 & 0 & 0 & \frac{1}{g}\\ 0 & 0 & 0 & \frac{1}{g} & -\frac{{\rm{\Delta }}}{{g}^{2}}\end{array}).$$

Then the effective Hamiltonian in the first subspace reduces to

$$\begin{array}{rcl}{H}_{{\rm{eff}}}^{1} & = & -\frac{{{\rm{\Omega }}}_{a}^{2}}{2{\rm{\Delta }}}\mathrm{|010}\rangle \langle \mathrm{010|}-\frac{{{\rm{\Omega }}}_{b}^{2}}{2{\rm{\Delta }}}\mathrm{|011}\rangle \langle \mathrm{011|}\\ & & -\frac{{{\rm{\Omega }}}_{a}{{\rm{\Omega }}}_{b}}{2{\rm{\Delta }}}\mathrm{(|011}\rangle \langle \mathrm{010|}+\mathrm{|010}\rangle \langle \mathrm{011|)}.\end{array}$$
(21)

The effective Hamiltonian in the second subspace

The inverse matrix of T2 in Eq. (9) is

$${T}_{2}^{-1}=(\begin{array}{cccccc}-\frac{{\rm{\Delta }}}{{\eta }_{+}} & \frac{g}{{\eta }_{+}} & 0 & 0 & 0 & 0\\ \frac{g}{{\eta }_{+}} & \frac{\sqrt{2}J}{{\eta }_{+}} & 0 & 0 & 0 & 0\\ 0 & 0 & -\frac{{\rm{\Delta }}}{{\eta }_{-}} & \frac{g}{{\eta }_{-}} & 0 & 0\\ 0 & 0 & \frac{g}{{\eta }_{-}} & -\frac{\sqrt{2}J}{{\eta }_{-}} & 0 & 0\\ 0 & 0 & 0 & 0 & -\frac{{\rm{\Delta }}}{{g}^{2}} & \frac{1}{g}\\ 0 & 0 & 0 & 0 & \frac{1}{g} & 0\end{array}),$$

where \({\eta }_{\pm }={g}^{2}\pm \sqrt{2}J{\rm{\Delta }}\). Based on Eq. (20), the effective Hamiltonian in the second subspace is given by

$$\begin{array}{rcl}{H}_{{\rm{eff}}}^{2} & = & \frac{1}{\frac{{g}^{4}}{{J}^{2}{\rm{\Delta }}}-2{\rm{\Delta }}}[{{\rm{\Omega }}}_{a}^{2}\mathrm{|000}\rangle \langle \mathrm{000|}+{{\rm{\Omega }}}_{b}^{2}\mathrm{|001}\rangle \langle \mathrm{001|}\\ & & +{{\rm{\Omega }}}_{a}{{\rm{\Omega }}}_{b}\mathrm{(|000}\rangle \langle \mathrm{001|}+\mathrm{|100}\rangle \langle \mathrm{000|)]}.\end{array}$$
(22)

Based on the above condition \(\{|{{\rm{\Omega }}}_{a}|,|{{\rm{\Omega }}}_{b}|\}\ll \{J,g,{\rm{\Delta }}\}\) and \(J\ll g\), this effective Hamiltonian \({H}_{{\rm{eff}}}^{2}\approx 0\).

The effective Hamiltonian in the third subspace

The inverse matrix of T3 in Eq. (12) is

$${T}_{3}^{-1}=(\begin{array}{ccccc}\sqrt{2}{\alpha }_{-}-2{\beta }^{2}{\rm{\Delta }} & 2{\beta }^{2}{\rm{\Delta }} & {\alpha }_{-} & \beta & \beta \\ 2{\beta }^{2}{\rm{\Delta }} & \sqrt{2}{\alpha }_{+}-2{\beta }^{2}{\rm{\Delta }} & {\alpha }_{+} & \beta & \beta \\ {\alpha }_{-} & {\alpha }_{+} & 2{\gamma }_{-}{\gamma }_{+}{\rm{\Delta }} & {\gamma }_{-} & {\gamma }_{+}\\ \beta & \beta & {\gamma }_{-} & \frac{1}{2{\rm{\Delta }}} & \frac{1}{2{\rm{\Delta }}}\\ \beta & \beta & {\gamma }_{+} & \frac{1}{2{\rm{\Delta }}} & \frac{1}{2{\rm{\Delta }}}\end{array}),$$

with \({\alpha }_{\pm }=\frac{\sqrt{2}{g}^{2}\pm 2J{\rm{\Delta }}}{4{J}^{2}{\rm{\Delta }}}\), \(\beta =-\,\frac{g}{2\sqrt{2}J{\rm{\Delta }}}\), and \({\gamma }_{\pm }=\frac{-{g}^{2}\pm 2J{\rm{\Delta }}}{2Jg{\rm{\Delta }}}\). Based on Eq. (20), the effective Hamiltonian in the third subspace can be evaluated explicitly

$${H}_{{\rm{eff}}}^{3}=0.$$
(23)

The effective Hamiltonian in the fourth subspace

The inverse matrix of T4 in Eq. (15) is

$${T}_{4}^{-1}=(\begin{array}{cccc}-\frac{1}{\sqrt{2}J} & 0 & -\frac{1}{2J} & 0\\ 0 & \frac{1}{\sqrt{2}J} & \frac{1}{2J} & 0\\ -\frac{1}{2J} & \frac{1}{2J} & -\frac{2{\rm{\Delta }}}{{g}^{2}} & -\frac{\sqrt{2}}{g}\\ 0 & 0 & -\frac{\sqrt{2}}{g} & 0\end{array}).$$

Based on Eq. (20), the effective Hamiltonian in the fourth subspace can be evaluated explicitly

$${H}_{{\rm{eff}}}^{4}=0.$$
(24)