Abstract
During this work, we demonstrate, for the first time, that the volumetric properties of pure ionic liquids could be truly predicted as a function of temperature from 219 K to 473 K and pressure up to 300 MPa. This has been achieved by using only density and isothermal compressibility data at atmospheric pressure through the Fluctuation Theory-based Tait-like Equation of State (FT-EoS). The experimental density data of 80 different ionic liquids, described in the literature by several research groups as a function of temperature and pressure, was then used to provide comparisons. Excellent predictive capability of FT-EoS was observed with an overall relative absolute average deviation close to 0.14% for the 15,298 data points examined during this work.
Similar content being viewed by others
Introduction
Ionic liquids (ILs) correspond to a large class of compounds with specific properties, such as high ionic conductivity, polarity, thermal and chemical stability, non-flammability and non-volatility1. Such unique profiles allow ILs to be good replacements for traditional organic solvents for various applications within the fields of catalysis2,3 and energy storage4, for example. A large number of research groups have then proved that applications could be then moved from laboratory scale to the industry5. To develop novel applications, it is vital to have access to their thermodynamic properties, such as the density, over a large range of temperature and pressure. Even if several groups have reported p-ρ-T data for several ILs6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82, these data are still lacking within respect to the possible number of IL combinations5. One solution to this problem is to develop novel models reliant on very few experimental data, based on a limited number of adjustable parameters and able to predict accurately ILs properties for a wide range of structures as a function of temperature and pressure. To date, different methods have been reported into the literature to correlate, evaluate and/or predict the volumetric properties of ILs29,53,66,70,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103. These methods are mainly based on (i) the group contribution model (GCM)53,83,84,85,86,87,88,89,90,91, (ii) the equation of state (EoS)29,66,70,92,93,94,95,96, (iii) the quantitative structure-property relationship (QSPR)97,98,99,100, (iv) the artificial neural network (ANN)101, and (v) simple cross correlations between density and other physical properties102,103. Even if all proposed methods showed good predictive capability they are, in general, developed within the prior knowledge of density data over a wide range of temperature and pressure. As high-pressure density data are still lacking and less accessible than equivalent data at atmospheric pressure, the development of a novel and simple model requesting only the temperature dependence on volumetric properties of ILs at atmospheric pressure is vital. Recently, such an approach, so called the Fluctuation Theory-based Tait-like Equation of State (FT-EoS), has been proposed to predict density data over a wide range of temperature and pressure using solely volumetric properties at atmospheric pressure104. Its high accuracy was already assessed to a wide range of substances including halogenated and polar liquids105,106,107. During this work, we decided to further assess its predictive capability for the high-pressure density of 80 different ILs using experimental data available into the literature as the function of temperature and pressure (see Supplementary Table S1)6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82.
Results
Herein, the density data of 80 different ionic liquids (ILs) were predicted and assessed using 15,298 data points from the literature (see Supplementary Table S1)6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82 using the Fluctuation Theory-based Tait-like Equation of State, which can be written along isotherms T = const as:
The reference pressure P 0 is assumed to be equal to atmospheric pressure; M and R are the molar mass and the gas constant, respectively. Two main control parameters in Eq. (1), v and k, are the functions of the density, ρ 0 and the isothermal compressibility \({\kappa }_{T}^{0}\) defined for each temperature as
at this pressure below the boiling temperature T b . They can be easily determined from experimental data as a reference state: the direct measurements of density, which give also the isobaric expansion coefficient \({\alpha }_{P}=-{\rho }_{0}^{-1}{(\partial {\rho }_{0}/\partial T)}_{P={P}_{0}}\) for T < T b . The last one combined with the measured speed of sound c 0 and the isobaric heat capacity \({c}_{P}^{0}\) provides the values of the isothermal compressibility
Thus, an application of Eq. (1) does not require, in principle, any high-pressure measurement or empiric correlations to determine these parameters, such unique behavior is, in fact, the main advantage of the proposed method in comparison with those already available in the literature29,53,66,70,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103.
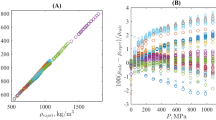
The practical application of the procedure described for an arbitrary T < T b , certainly requires introduction of some continual function fitting the discrete set of experimental data. During this work, various density and isothermal compressibility datasets at atmospheric pressure were used then to truly predicted the volumetric properties of 80 selected ILs as a function of temperature from 219 K to 473 K and pressure up to 300 MPa. As reported in the Supplementary Table S2, these atmospheric pressure input data, especially for the density, are mainly coming directly from the reported literature values. However, in some cases, no isothermal compressibility value was originally reported for a given IL structure studied solely by one research group, for example. In such a situation, this missing input has been determined herein at atmospheric pressure following this order of preference (i) by applying the Tait equation for reported density values; (ii) by using Eq. (3) if the speed of sound and the isobaric heat capacity were also reported in the reference paper; or alternatively, when (i) and (ii) were not applicable, by applying the GCM proposed by Jacquemin et al.53,83. As shown in Fig. 1 and depicted in the ESI for each investigated IL, by applying this data collection methodology, 1,377 data points were used to correlate the temperature dependence on the density at atmospheric pressure by cubic polynomials within an excellent accuracy close to 0.02%. However, as no density value was reported at atmospheric pressure for the ILs [C6mim][OTf]14, [C4mim][(C2F5)3PF3]68, [C6mim][(C2F5)3PF3]68, and [P66614][OAc]65; in these cases, requested data were evaluated by using the GCM developed by Jacquemin et al.53,83.
Comparison of experimental and correlated density data using Eq. (13) at atmospheric pressure for selected ionic liquids.
Similarly, the temperature dependence on the ILs isothermal compressibility was correlated using data directly reported in the literature, or, alternatively, calculated using the approach stated above (i.e. using the Tait equation, or using thermodynamics formalism or using the GCM developed by Jacquemin et al.53,83) as reported in the Supplementary Table S2. By applying this FT-EoS approach for selected ILs, as shown in Fig. 2 and exemplified in the ESI for each IL, excellent agreement is observed between experimental6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82, and predicted high-pressure density data for all ILs investigated during this work.
This excellent predictive capability was attested by comparing 13,921 high-pressure density data points from the literature for the 80 ILs with those predicted by this method within an overall relative average absolute deviation (RAAD) close to 0.14%. Furthermore, this overall RAAD value also attests the higher ability of this FT-EoS to truly predict the volumetric properties of ILs over a wide range of temperature and pressure in comparison with other models reported in the literature29,53,66,70,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103, to date. For example, in the case of the [C4mim][NTf2], e.g. one of the most studied IL, an overall RAAD close to 0.06% is observed between data reported in the literature15,26,50,55,56,81,82, with those determined herein using the FT-EoS equation, while RAADs close to 0.48%, 0.29%, 0.20%, 0,47%, 0.33% are observed using the methods reported by Jacquemin et al.53, Paduszyński et al.90, Gardas et al.86, Lazzuz87, Qiao et al.88, respectively. This is further attested by comparing also the number of adjustable parameters associated to these reported models, while only two input pairs of parameters (e.g. temperature dependences on the density and on the isothermal compressibility at atmospheric pressure) are requested for the proposed FT-EoS.
Discussion
By depicting comparisons made within the literature, as shown in Supplementary Tables S1 and S2, it appears that larger errors are observed for: (i) ILs density data described by more than one research group; (ii) hydrophilic and/or water sensitive ILs and (iii) datasets predicted using GCM density data at atmospheric pressure. For example, the largest RAAD, which is close to 1.8%, was observed for the [C2mim][PF6] using extrapolated density data at atmospheric pressure reported by Taguchi et al.12. Similarly, using the high-pressure data reported by Klomfar et al.14 for the [C2mim][BF4] along with atmospheric input data reported by Gardas et al.11 a RAAD close to 1.3% was achieved, while excellent agreements were observed with other datasets published in the literature for this IL (0.02%11,0.03%13,and 0.13%12). In the case of the [C4mim][BF4], larger deviations were observed between predicted density values with datasets reported by Tekin et al.25,28. (RAAD = 0.99% for the two identical datasets published by this group) and by Harris et al.27. (RAAD = 0.88%) while RAAD better than 0.3% were observed for the other datasets13,21,22,23,24,26,29,30,31,32,33,34 available in the literature showing a clear discrepancy between the experimental data of this water sensitive IL39. Interestingly, it appears that the missing input data at atmospheric pressure could, a priori, be evaluated by the GCM developed by Jacquemin et al.53,83 and then used in the FT-EoS to predict accurately high-pressure density data as exemplified for the [C6mim][OTf] (RAAD = 1.04%14), [C4mim][(C2F5)3PF3] (RAAD = 0.02%68), [C6mim][(C2F5)3PF3] (RAAD = 0.16%68), and [P66614][OAc] (RAAD = 0.61%65), for example. Similarly, as demonstrated herein in the case of the [C4mim][PF6], high-pressure speeds of sound could be used to determine the ILs isothermal compressibility data at atmospheric pressure, which could be then used as the input data for the FT-EoS. For example, by using the calculated isothermal compressibility reported by Gomes de Azevedo et al.22, excellent agreement is observed between predicted and experimental [C4mim][PF6] high-pressure density data published by Jacquemin et al.26 (RAAD = 0.14%), Machida et al.29 (RAD = 0.19%) and Tomida et al.79 (RAAD = 0.06%). Interestingly, by comparing input data determined thanks to the thermodynamics formalism (Eq. (3))22 and those from the GCM developed by Jacquemin et al.53,83 RAAD close to 1.5% on their calculated isothermal compressibility data for the [C4mim][PF6] is observed (see Supplementary Table S3). These two approaches lead then to a RAAD between the high-pressure density data reported by Azevedo et al.22 and those calculated herein using the FT-EOS close to 0.02% or 0.01% using isothermal compressibility data from the Eq. (3) or the Jacquemin et al. GCM53,83, respectively (see Supplementary Figure S1). This furthermore highlights the possibility to determine missing isothermal compressibility input by following one of these two approaches with a great accuracy.
Finally, by comparing the performance of the proposed FT-EoS approach with other methods described in the literature, it appears that a better prediction of high-pressure density data is achieved by using the FT-EoS presented herein, compared to those reached using GCMs available in the literature as an overall RAAD close to 0.36%, 0.45% or better than 1.45% was reported by Jacquemin et al.53, Paduszyński et al.90 or Gardas et al.86, for example. Nevertheless, the main advantage of these GCMs is to be able to estimate the density of unknown ILs, which is not the case of the FT-EoS. However, as exemplified herein, it is possible to combine these two approaches by evaluating the requested input data at atmospheric pressure using a GCM to feed the FT-EoS for unknown IL structures demonstrating the great potential of the FT-EoS approach described in this work.
Method
Briefly, the FT-EOS acts in the context of thermodynamic approaches to the derivation of an equation of state based on the consideration of the reduced elastic bulk modulus \(K={\kappa }_{T}^{-1}\), where the isothermal compressibility is defined as:
expressing the changes of specific volume V = ρ −1 or density caused by the change of the external pressure applied to a fluid.
This approach generalizes the stress-strain relationship from the classic theory of elasticity108, where the small homogeneous compression gives in the linear approximation: u ii = (3K 0)−1 σ ii . Here, the sum of diagonal elements of the strain tensor u ii describes the relative change in the volume while the stress tensor is equal to σ ik = −pδ ik (where δ ik is the Kronecker symbol, and p = dP is the excess applied pressure). As a result, this elastic bulk modulus satisfies Hooke’s law:
where V 0 denotes the strainless volume, and K 0 = const independent on the pressure for infinitesimal deformations.
By considering finite deformations of liquids, Tait109 proposed the following linear correction, which could be applied with the respect to the pressure change:
where \({P}_{0}\) is the reference ambient pressure at the uncompressed state.
The differential replacement of finite differences proposed by Tammann110
gives after integration the classic Tait equation, which can be written in terms of density ρ = V −1 as follows:
The Tait equation Eq. (8) relates to the isothermal compression to the initial reference state, where the parameter \({K}_{0}^{-1}={\kappa }_{T}^{0}\) is the isothermal compressibility under the reference pressure P 0. One can highlight, however, that such an assumption results in the non-physical existence of the maximal pressure P max, which corresponds to ρ = ∞ (V = 0) and negative values of the density/volume for larger pressures, although these parameters are extremely high for reasonable practical applications. In addition, K′ remains, in Eq. (8), a purely empirical parameter111.
Note that there is an alternative to the choice of the reference volume, which allows for avoiding the mentioned negative densities, when the specific volume of the compressed medium is chosen instead of the initial one, as proposed by Murnaghan112 in the context of the compressibility of elastic solids under extremely high pressures, that also can been applied to liquids111. But such an approach keeps at last one purely empirical constant too and has a similar range of accuracy as the Tait equation for low elevated pressures.
Thus, Eq. (9), given below, could be then obtained by replacing the fraction of the original Tait equation (Eq. (8)) by the first terms of its Taylor’s expansion taking into account the fact that the subtrahend in the denominator is a small quantity for realistic PρT conditions of liquids.
This form is free from non-physical negative density values and implies the exponential functional dependence along isotherms (∂ρ/∂P) T ~exp(−kρ) with \(k=K^{\prime} {\rho }_{0}^{-1}\).
Quantitatively, there is an experimental evidence for a large variety of classes of liquids105,107,113,114 that the accurate exponential dependence for different temperatures fulfils for the dimensionless complex:
where T, M and R are the temperature, the molar mass and the gas constant.
The original Eq. (1), used therein to predict the volumetric properties of ILs as a function of temperature and pressure, is obtained by expressing K′ and \({\kappa }_{T}^{0}\) through k and v.
Note also that Eq. (10) has a statistical meaning as an inverse ratio of the relative volume fluctuation to its value in the hypothetical case where the liquid acts as an ideal gas for the same temperature-volume parameters \({\nu }^{-1}=\langle {\rm{\Delta }}{V}^{2}\rangle /\langle {\rm{\Delta }}{V}_{ig}^{2}\rangle \) (see refs104,113 for details), or as a ratio of the corresponding elastic isothermal bulk moduli v = K/K ig , since K ig = M −1 ρRT.
Therefore, from the point of view of the linear expansion of the elastic bulk modulus with respect to the pressure, Eq. (9) leads to the following relation:
The right-hand side of Eq. (11) can be considered as a weighted average of the solid state (Hooke’s equation) and an ideal gas moduli (K ig = M −1 ρRT = P, from the Clapeyron’s EoS) multiplied by the ratio of volumes, which provides a more accurate representation of the stress-strain conditions since both coefficients K and K′ are defined for uncompressed state, and K(p) for a compressed state. In fact, this ratio compensates for the difference between the force densities acting within these two states. This allows for interpreting of the origin of the pressure-dependent bulk modulus Eq. (11). As a bulk modulus of composite medium is formed by elastic dense molecular complexes separated by holes, i.e. an ideal gas of compressible clusters (see ref.113 for simulations of lattice liquid system in comparison with saturated liquefied noble gases behavior, and115 for some more abstract theory of similar systems. This conclusion is also supported by the experimental fact of violation of such exponential dependence at high pressures corresponding to the conditions of contact percolation transition116.
Since the parameter k can be determined as a local (pointwise) slope of the tangent to the function logv = kρ 0 + b, which can be calculated from experimental data measured at atmospheric pressure for those temperatures, this approach requires some special improvements in the procedure of parameter determination for the FT-EoS Eq. (1).
The desired derivative was calculated using the following parametric differentiation:
One can see that Eq. (12) formally contains the derivative of dimensional isothermal compressibility, however, the selected κ T unit does not influence completely the solution of Eq. (12) due to the presence of the logarithm function. To exemplify this point let us represent \({\kappa }_{T}={\tilde{\kappa }}_{T}(T)[{\kappa }_{T}]\), where \({\tilde{\kappa }}_{T}(T)\) and [κ T ] denote the functional temperature dependence and the selected unit (arbitrary selected but the same unit must be used for all investigated temperature points) of κ T data, respectively. Whence, \(\frac{d\,\mathrm{log}\,{\kappa }_{T}}{dT}=\frac{d\,\mathrm{log}\,{\tilde{\kappa }}_{T}}{dT}+\frac{d\,\mathrm{log}\,[{\kappa }_{T}]}{dT}=\frac{d\,\mathrm{log}\,{\tilde{\kappa }}_{T}}{dT}\) since \(\mathrm{log}({\tilde{\kappa }}_{T}(T)[{\kappa }_{T}])=\) \(\mathrm{log}\,{\tilde{\kappa }}_{T}(T)+\,\mathrm{log}\,[{\kappa }_{T}]\,{\rm{and}}\,\mathrm{log}\,[{\kappa }_{T}]={\rm{const}}\). For the same reason, Eq. (12) does not contain the combination M/R, as expected by combining Eq. (10) into Eq. (12).
In practice, the density and the logarithm of the isothermal compressibility can be fitted with a high accuracy within appropriate temperature intervals by quadratic polynomials of the temperature:
Therefore, Eqs (10) and (12) take the forms, respectively
and
Finally, the values given by Eqs (14) and (15) for each temperature should be substituted into Eq. (1), as well as, the density at atmospheric pressure to determine explicitly the density at a given temperature and pressure.
During this work, practical calculations were performed with a user-defined function written in VBA language for MS Excel (see Supplementary spreadsheet FT-EoS_calc_template.xlsm). The input variables are the pairs “temperature-density” and “temperature-isothermal compressibility” filled by experimental data measured at the normal atmospheric pressure (at least 4 data points are requested) processed to obtain the coefficients in Eq. (13) via the least-square polynomial fit using the build-in MS Excel procedure (Application.LinEst). They are used subsequently in Eqs (14) and (15), which are substituted into the final expression (Eq. (1)) applied for the predictive calculation of the density.
Data availability
A summary of all the experimental data collected from the literature, data input used, methodology applied and obtained prediction results are presented in Supplementary Tables S1–S3 and illustrated in Figure S1 in the case of the [C4mim][PF6]. The supplementary MS Excel spreadsheet FT-EoS_calc_template.xlsm contains the build-in VB procedure (FTEOS) allows calculation of high-pressure density of liquids using fluctuation equation of state.
Conclusion
In the light of this work, one can conclude that the proposed FT-EoS approach can be used to truly predict with a high accuracy the density of liquids under elevated pressures. This approach requests, solely, the prior knowledge of the temperature dependences on physical data (such as the speed of sound, the density, and the isobaric heat capacity) at normal ambient atmospheric pressure, which can be easily obtained experimentally. One can further note that this approach is not based on a pure correlation but on the general elastic properties of isothermal compression of elastic media. Finally, the validity of this method has been checked herein through the comparison between predicted and experimental high-pressure density data for an extensive set of data covering a large range of temperatures and pressures for 80 different ionic liquids within an accuracy close to 0.14%.
Change history
22 November 2017
A correction to this article has been published and is linked from the HTML version of this paper. The error has been fixed in the paper.
References
Aparicio, S., Atilhan, M. & Karadas, F. Thermophysical Properties of Pure Ionic Liquids: Review of Present Situation. Ind. Eng. Chem. Res. 49, 9580–9595 (2010).
Zhang, Q., Zhang, S. & Deng, Y. Recent Advances in Ionic Liquid Catalysis. Green Chem. 13, 2619–2637 (2011).
Pârvulescu, V. I. & Hardacre, C. Catalysis in Ionic Liquids. Chem. Rev. 107, 2615–2665 (2007).
MacFarlane, D. R. et al. Energy Applications of Ionic Liquids. Energy Environ. Sci. 7, 232–250 (2014).
Plechkova, N. V. & Seddon, K. R. Applications of Ionic Liquids in the Chemical Industry. Chem. Soc. Rev. 37, 123–150 (2008).
Królikowska, M. & Hofman, T. Densities, Isobaric Expansivities and Isothermal Compressibilities of the Thiocyanate-Based Ionic Liquids at Temperatures (298.15-338.15 K) and Pressures up to 10 MPa. Thermochim. Acta 530, 1–6 (2012).
Stevanovic, S., Podgoršek, A., Pádua, A. A. H. & Costa Gomes, M. F. Effect of Water on the Carbon Dioxide Absorption by 1-Alkyl-3-Methylimidazolium Acetate Ionic Liquids. J. Phys. Chem. B 116, 14416–14425 (2012).
Machida, H., Ryosuke, T., Sato, Y. & Smith, R. L. J. Measurement and Correlation of High Pressure Densities of Ionic Liquids, 1-Ethyl-3-Methylimidazolium L-Lactate ([emim][Lactate]), 2-Hydroxyethyl-Trimethylammonium L-Lactate ([(C2H4OH)(CH3)3N][Lactate]), and 1-Butyl-3-Methylimidazolium Chloride ([bmim][Cl]). J. Chem. Eng. Data 56, 923–928 (2011).
Klomfar, J., Součková, M. & Pátek, J. P–ρ–T Measurements for 1-Ethyl and 1-Butyl-3-Methylimidazolium Dicyanamides from Their Melting Temperature to 353 K and up to 60 MPa in Pressure. J. Chem. Eng. Data 57, 1213–1221 (2012).
Freire, M. G. et al. Thermophysical Characterization of Ionic Liquids Able to Dissolve Biomass. J. Chem. Eng. Data 56, 4813–4822 (2011).
Gardas, R. L. et al. PρT Measurements of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 52, 1881–1888 (2007).
Taguchi, R., Machida, H., Sato, Y. & Smith, R. L. High-Pressure Densities of 1-Alkyl-3-Methylimidazolium Hexafluorophosphates and 1-Alkyl-3-Methylimidazolium Tetrafluoroborates at Temperatures from (313 to 473) K and at Pressures up to 200 MPa. J. Chem. Eng. Data 54, 22–27 (2009).
Sanmamed, Y. A. et al. Experimental Methodology for Precise Determination of Density of RTILs as a Function of Temperature and Pressure Using Vibrating Tube Densimeters. J. Chem. Thermodyn. 42, 553–563 (2010).
Klomfar, J., Součková, M. & Pátek, J. P–ρ–T Measurements for 1-Alkyl-3-Methylimidazolium-Based Ionic Liquids with Tetrafluoroborate and a Trifluoromethanesulfonate Anion. J. Chem. Eng. Data 57, 708–720 (2012).
Nieto de Castro, C. A. et al. Studies on the Density, Heat Capacity, Surface Tension and Infinite Dilution Diffusion with the Ionic Liquids [C4mim][NTf2], [C4mim][dca], [C2mim][EtOSO3] and [Aliquat][dca]. Fluid Phase Equilib 294, 157–179 (2010).
Gołdon, A., Dąbrowska, K. & Hofman, T. Densities and Excess Volumes of the 1,3-Dimethylimidazolium Methylsulfate + Methanol System at Temperatures from (313.15 to 333.15) K and Pressures from (0.1 to 25) MPa. J. Chem. Eng. Data 52, 1830–1837 (2007).
Aparicio, S., Alcalde, R., García, B. & Leal, J. M. High-Pressure Study of the Methylsulfate and Tosylate Imidazolium Ionic Liquids. J. Phys. Chem. B 113, 5593–5606 (2009).
Tome, L. I. N. et al. Measurements and Correlation of High-Pressure Densities of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 53, 1914–1921 (2008).
Gu, Z. & Brennecke, J. F. Volume Expansivities and Isothermal Compressibilities of Imidazolium and Pyridinium-Based Ionic Liquids. J. Chem. Eng. Data 47, 339–345 (2002).
Tomida, D., Kenmochi, S., Qiao, K., Tsukada, T. & Yokoyama, C. Densities and Thermal Conductivities of N-AlkylpyridiniumTetrafluoroborates at High Pressure. Fluid Phase Equilib. 340, 31–36 (2013).
Rebelo, L. P. N. et al. A Detailed Thermodynamic Analysis of [C4mim][BF4] + Water as a Case Study to Model Ionic Liquid Aqueous Solutions. Green Chem. 6, 369–381 (2004).
Gomes de Azevedo, R. et al. Thermophysical and Thermodynamic Properties of 1-Butyl-3-Methylimidazolium Tetrafluoroborate and 1-Butyl-3-Methylimidazolium Hexafluorophosphate over an Extended Pressure Range. J. Chem. Eng. Data 50, 997–1008 (2005).
Tomida, D., Kumagai, A., Qiao, K. & Yokoyama, C. Viscosity of [bmim][PF6] and [bmim][BF4] at High Pressure. Int. J. Thermophys. 27, 39–47 (2006).
Gardas, R. L. et al. High-Pressure Densities and Derived Thermodynamic Properties of Imidazolium-Based Ionic Liquids. J. Chem. Eng. Data 52, 80–88 (2007).
Tekin, A., Safarov, J., Shahverdiyev, A. & Hassel, E. (P, ρ, T) Properties of 1-Butyl-3-Methylimidazolium Tetrafluoroborate and 1-Butyl-3-Methylimidazolium Hexafluorophosphate at T = (298.15 to 398.15) K and Pressures up to p = 40 MPa. J. Mol. Liq. 136, 177–182 (2007).
Jacquemin, J., Husson, P., Mayer, V. & Cibulka, I. High-Pressure Volumetric Properties of Imidazolium-Based Ionic Liquids: Effect of the Anion. J. Chem. Eng. Data 52, 2204–2211 (2007).
Harris, K. R., Kanakubo, M. & Woolf, L. A. Temperature and Pressure Dependence of the Viscosity of the Ionic Liquid 1-Butyl-3-Methylimidazolium Tetrafluoroborate: Viscosity and Density Relationships in Ionic Liquids. J. Chem. Eng. Data 52, 2425–2430 (2007).
Abdulagatov, I. M., Tekin, A., Safarov, J., Shahverdiyev, A. & Hassel, E. Densities and Excess, Apparent, and Partial Molar Volumes of Binary Mixtures of BMIMBF4 + Ethanol as a Function of Temperature, Pressure, and Concentration. Int. J. Thermophys. 29, 505–533 (2008).
Machida, H., Sato, Y. & Smith, R. L. Pressure-Volume-Temperature (PVT) Measurements of Ionic Liquids ([bmim+][PF6 −], [bmim+][BF4 −], [bmim+][OcSO4 −]) and Analysis with the Sanchez-Lacombe Equation of State. Fluid Phase Equilib 264, 147–155 (2008).
Han, C., Xia, S., Ma, P. & Zeng, F. Densities of Ionic Liquid [BMIM][BF4] + Ethanol, + Benzene, and + Acetonitrile at Different Temperature and Pressure. J. Chem. Eng. Data 54, 2971–2977 (2009).
Rilo, E., Ferreira, A. G. M., Fonseca, I. M. A. & Cabeza, O. Densities and Derived Thermodynamic Properties of Ternary Mixtures 1-Butyl-3-Methyl-Imidazolium Tetrafluoroborate + ethanol + water at Seven Pressures and Two Temperatures. Fluid Phase Equilib 296, 53–59 (2010).
Currás, M. R. et al. Behavior of the Environmentally Compatible Absorbent 1-Butyl-3-Methylimidazolium Tetrafluoroborate with 2,2,2-Trifluoroethanol: Experimental Densities at High Pressures and Modeling of PVT and Phase Equilibria Behavior with PC-SAFT EoS. Ind. Eng. Chem. Res 50, 4065–4076 (2011).
Klomfar, J., Součková, M. & Pátek, J. Experimental P-ρ-T Data for 1-Butyl-3-Methylimidazolium Tetrafluoroborate at Temperatures from (240 to 353) K and at Pressures up to 60 MPa. J. Chem. Eng. Data 56, 426–436 (2011).
Matkowska, D. & Hofman, T. High-Pressure Volumetric Properties of Ionic Liquids: 1-Butyl-3-Methylimidazolium Tetrafluoroborate, [C4mim][BF4], 1-Butyl-3-Methylimidazolium Methylsulfate [C4mim][MeSO4] and 1-Ethyl-3-Methylimidazolium Ethylsulfate, [C2mim][EtSO4]. J. Mol. Liq. 165, 161–167 (2012).
Hofman, T., Gołdon, A., Nevines, A. & Letcher, T. M. Densities, Excess Volumes, Isobaric Expansivity, and Isothermal Compressibility of the (1-Ethyl-3-Methylimidazolium Ethylsulfate + methanol) System at Temperatures (283.15 to 333.15) K and Pressures from (0.1 to 35) MPa. J. Chem. Thermodyn. 40, 580–591 (2008).
Matkowska, D., Golłdon, A. & Hofman, T. Densities, Excess Volumes, Isobaric Expansivities, and Isothermal Compressibilities of the 1-Ethyl-3-Methylimidazolium Ethylsulfate + Ethanol System at Temperatures (283.15 to 343.15) K and Pressures from (0.1 to 35) MPa. J. Chem. Eng. Data 55, 685–693 (2010).
Regueira, T., Lugo, L. & Fernández, J. High Pressure Volumetric Properties of 1-Ethyl-3-Methylimidazolium Ethylsulfate and 1-(2-Methoxyethyl)-1-Methyl-Pyrrolidinium Bis(trifluoromethylsulfonyl)imide. J. Chem. Thermodyn. 48, 213–220 (2012).
Schmidt, H. et al. Experimental Study of the Density and Viscosity of 1-Ethyl-3-Methylimidazolium Ethyl Sulfate. J. Chem. Thermodyn. 47, 68–75 (2012).
Jacquemin, J. & Husson, P. Comments and Additional Work on ‘High-Pressure Volumetric Properties of Imidazolium-Based Ionic Liquids: Effect of the Anion’. J. Chem. Eng. Data 57, 2409–2414 (2012).
Carvalho, P. J. et al. High Pressure Density and Solubility for the CO2 + 1-Ethyl-3-Methylimidazolium Ethylsulfate System. J. Supercrit. Fluids 88, 46–55 (2014).
Guerrero, H., García-Mardones, M., Cea, P., Lafuente, C. & Bandrés, I. Correlation of the Volumetric Behaviour of Pyridinium-Based Ionic Liquids with Two Different Equations. Thermochim. Acta 531, 21–27 (2012).
Safarov, J., Kul, I., El-Awady, W. A., Shahverdiyev, A. & Hassel, E. Thermodynamic Properties of 1-Butyl-3-Methylpyridinium Tetrafluoroborate. J. Chem. Thermodyn. 43, 1315–1322 (2011).
Safarov, J. et al. Thermophysical Properties of 1-Butyl-4-Methylpyridinium Tetrafluoroborate. J. Chem. Thermodyn. 51, 82–87 (2012).
Safarov, J. & Hassel, E. Thermodynamic Properties of 1-Hexyl-3-Methylimidazolium Tetrafluoroborate. J. Mol. Liq. 153, 153–158 (2010).
Gardas, R. L. et al. Densities and Derived Thermodynamic Properties of Imidazolium-, Pyridinium-, Pyrrolidinium-, and Piperidinium-Based Ionic Liquids. J. Chem. Eng. Data 53, 805–811 (2008).
Harris, K. R., Kanakubo, M. & Woolf, L. A. Temperature and Pressure Dependence of the Viscosity of the Ionic Liquids 1-Methyl-3-Octylimidazolium Hexafluorophosphate and 1-Methyl-3-Octylimidazolium Tetrafluoroborate. J. Chem. Eng. Data 51, 1161–1167 (2006).
Kanakubo, M., Harris, K. R., Tsuchihashi, N., Ibuki, K. & Ueno, M. Temperature and Pressure Dependence of the Electrical Conductivity of the Ionic Liquids 1-Methyl-3-Octylimidazolium Hexafluorophosphate and 1-Methyl-3-Octylimidazolium Tetrafluoroborate. Fluid Phase Equilib 261, 414–420 (2007).
Harris, K. R., Woolf, L. A. & Kanakubo, M. Temperature and Pressure Dependence of the Viscosity of the Ionic Liquids 1-Butyl-3-methylimidazolium Hexafluorophosphate. J. Chem. Eng. Data 50, 1777–1782 (2005).
Tomida, D., Kumagai, A., Kenmochi, S., Qiao, K. & Yokoyama, C. Viscosity of 1-Hexyl-3-Methylimidazolium Hexafluorophosphate and 1-Octyl-3-Methylimidazolium Hexafluorophosphate at High Pressure. J. Chem. Eng. Data 52, 577–579 (2007).
Harris, K. R., Kanakubo, M. & Woolf, L. A. Temperature and Pressure Dependence of the Viscosity of the Ionic Liquids 1-Hexyl-3-Methylimidazolium Hexafluorophosphate and 1-Butyl-3-Methylimidazolium Bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 52, 1080–1085 (2007).
Dávila, M. J., Aparicio, S., Alcalde, R., García, B. & Leal, J. M. On the Properties of 1-Butyl-3-Methylimidazolium Octylsulfate Ionic Liquid. Green Chem. 9, 221–232 (2007).
Safarov, J., El-Awady, W. A., Shahverdiyev, A. & Hassel, E. Thermodynamic Properties of 1-Ethyl-3-Methylimidazolium Bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 56, 106–112 (2011).
Jacquemin, J. et al. Prediction of Ionic Liquid Properties. II. Volumetric Properties as a Function of Temperature and Pressure. J. Chem. Eng. Data 53, 2133–2143 (2008).
Esperança, J. M. S. S. et al. Density, Speed of Sound, and Derived Thermodynamic Properties of Ionic Liquids over an Extended Pressure Range. 4. [C3mim][NTf2] and [C5mim][NTf2]. J. Chem. Eng. Data 51, 2009–2015 (2006).
Widowati, E. & Lee, M.-J. P–V–T Properties of Binary Mixtures of the Ionic Liquid 1-Butyl-3-Methylimidazolium Bis(trifluoromethylsulfonyl)imide with Anisole or Acetophenone at Elevated Pressures. J. Chem. Thermodyn. 63, 95–101 (2013).
Gomes de Azevedo, R. et al. Thermophysical and Thermodynamic Properties of Ionic Liquids over an Extended Pressure Range: [bmim][NTf2] and [hmim][NTf2]. J. Chem. Thermodyn. 37, 888–899 (2005).
Harris, K. R., Woolf, L. A., Kanakubo, M. & Rüther, T. Transport Properties of N-Butyl-N-MethylpyrrolidiniumBis(trifluoromethylsulfonyl)amide. J. Chem. Eng. Data 56, 4672–4685 (2011).
Regueira, T., Lugo, L. & Fernández, J. Influence of the Pressure, Temperature, Cation and Anion on the Volumetric Properties of Ionic Liquids: New Experimental Values for Two Salts. J. Chem. Thermodyn 58, 440–448 (2013).
Widowati, E. & Lee, M.-J. PVT Properties for Binary Ionic Liquids of 1-Methyl-1-Propylpiperidinium Bis(trifluoromethylsulfonyl)imide with Anisole or Acetophenone at Pressures up to 50MPa. J. Chem. Thermodyn. 49, 54–61 (2012).
Kandil, M. E., Marsh, K. N. & Goodwin, A. R. H. Measurement of the Viscosity, Density, and Electrical Conductivity of 1-Hexyl-3-Methylimidazolium Bis(trifluorosulfonyl)imide at Temperatures between (288 and 433) K and Pressures below 50 MPa. J. Chem. Eng. Data 52, 2382–2387 (2007).
Esperança, J. M. S. S., Guedes, H. J. R., Lopes, J. N. C. & Rebelo, L. P. N. Pressure−Density−Temperature (P−ρ−T) Surface of [C6mim][NTf2]. J. Chem. Eng. Data 53, 867–870 (2008).
Iguchi, M. et al. Measurement of High-Pressure Densities and Atmospheric Viscosities of Ionic Liquids: 1-Hexyl-3-Methylimidazolium Bis(trifluoromethylsulfonyl)imide and 1-Hexyl-3-Methylimidazolium Chloride. J. Chem. Eng. Data 59, 709–717 (2014).
Safarov, J. et al. Thermophysical Properties of 1-Hexyl-3-Methylimidazolium Bis(trifluoromethylsulfonyl)imide at High Temperatures and Pressures. J. Mol. Liq. 187, 137–156 (2013).
Almantariotis, D., Fandiño, O., Coxam, J.-Y. & Costa Gomes, M. F. Direct Measurement of the Heat of Solution and Solubility of Carbon Dioxide in 1-Hexyl-3-Methylimidazolium Bis[trifluoromethylsulfonyl]amide and 1-Octyl-3-Methylimidazolium Bis[trifluoromethylsulfonyl]amide. Int. J. Greenh. Gas Control 10, 329–340 (2012).
Esperança, J. M. S. S., Guedes, H. J. R., Blesic, M. & Rebelo, L. P. N. Densities and Derived Thermodynamic Properties of Ionic Liquids. 3. Phosphonium-Based Ionic Liquids over an Extended PressureRange. J. Chem. Eng. Data 51, 237–242 (2006).
Gonçalves, F. A. M. M. et al. Pressure-Volume-Temperature Measurements of Phosphonium-Based Ionic Liquids and Analysis with Simple Equations of State. J. Chem. Thermodyn. 43, 914–929 (2011).
Tome, L. I. N. et al. Measurements and Correlation of High-Pressure Densities of Phosphonium Based Ionic Liquids. J. Chem. Eng. Data 56, 2205–2217 (2011).
Almantariotis, D. et al. Absorption of Carbon Dioxide, Nitrous Oxide, Ethane and Nitrogen by 1-Alkyl-3-Methylimidazolium (Cnmim, n = 2,4,6) Tris(pentafluoroethyl)trifluorophosphate Ionic Liquids (eFAP). J. Phys. Chem. B 116, 7728–7738 (2012).
Stevanovic, S. & Costa Gomes, M. F. Solubility of Carbon Dioxide, Nitrous Oxide, Ethane, and Nitrogen in 1-Butyl-1-Methylpyrrolidinium and Trihexyl(tetradecyl)phosphoniumTris(pentafluoroethyl)-trifluorophosphate (eFAP) Ionic Liquids. J. Chem. Thermodyn. 59, 65–71 (2013).
Ferreira, C. E., Talavera-Prieto, N. M. C., Fonseca, I. M. A., Portugal, A. T. G. & Ferreira, A. G. M. Measurements of pVT, Viscosity, and Surface Tension of TrihexyltetradecylphosphoniumTris(pentafluoroethyl)trifluorophosphate Ionic Liquid and Modelling with Equations of State. J. Chem. Thermodyn. 47, 183–196 (2012).
Klomfar, J., Součková, M. & Pátek, J. Temperature Dependence Measurements of the Density at 0.1 MPa for 1-Alkyl-3-Methylimidazolium-Based Ionic Liquids with the Trifluoromethanesulfonate and Tetrafluoroborate Anion. J. Chem. Eng. Data 55, 4054–4057 (2010).
Gaciño, F. M., Regueira, T., Comuñas, M. J. P., Lugo, L. & Fernández, J. Density and Isothermal Compressibility for Two Trialkylimidazolium-Based Ionic Liquids at Temperatures from (278 to 398)K and up to 120MPa. J. Chem. Thermodyn. 81, 124–130 (2015).
Talavera-Prieto, N. M. C. et al. Thermophysical Characterization of N-Methyl-2-Hydroxyethylammonium Carboxilate Ionic Liquids. J. Chem. Thermodyn. 68, 221–234 (2014).
Gaciño, F. M. et al. Volumetric Behaviour of Six Ionic Liquids from T = (278 to 398)K and up to 120MPa. J. Chem. Thermodyn. 93, 24–33 (2016).
Guerrero, H., Martín, S., Pérez-Gregorio, V., Lafuente, C. & Bandrés, I. Volumetric Characterization of Pyridinium-Based Ionic Liquids. Fluid Phase Equilib 317, 102–109 (2012).
Engelmann, M., Schmidt, H., Safarov, J., Nocke, J. & Hassel, E. Thermal Properties of 1-Butyl-3-Methylimidazolium Dicyanamide at High Pressures and Temperatures. Acta Chim. Slovaca 5, 86–94 (2012).
Hiraga, Y. et al. Separation Factors for [amim]Cl–CO2 Biphasic Systems from High Pressure Density and Partition Coefficient Measurements. Sep. Purif. Technol. 155, 139–148 (2015).
Matkowska, D. & Hofman, T. Volumetric Properties of the {x1[C4mim][MeSO4] + (1 - x1)MeOH} System at Temperatures from (283.15 to 333.15) K and Pressures from (0.1 to 35) MPa. J. Solution Chem 42, 979–990 (2013).
Tomida, D., Kenmochi, S., Tsukada, T., Qiao, K. & Yokoyama, C. Thermal Conductivities of [bmim][PF6], [hmim][PF6], and [omim][PF6] from 294 to 335 K at Pressures up to 20 MPa. Int. J. Thermophys. 28, 1147–1160 (2007).
Abdulagatov, I. M., Safarov, J., Guliyev, T. & Shahverdiyev, A. & Hassel, E. High Temperature and High Pressure Volumetric Properties of (Methanol + [BMIM+][OcSO4 −]) Mixtures. Phys. Chem. Liq. 47, 9–34 (2009).
Kanakubo, M. & Harris, K. R. Density of 1-Butyl-3-Methylimidazolium Bis(trifluoromethanesulfonyl)amide and 1-Hexyl-3-Methylimidazolium Bis(trifluoromethanesulfonyl)amide over an Extended Pressure Range up to 250 MPa. J. Chem. Eng. Data 60, 1408–1418 (2015).
Hiraga, Y., Kato, A., Sato, Y. & Smith, R. L. Densities at Pressures up to 200 MPa and Atmospheric Pressure Viscosities of Ionic Liquids 1-Ethyl-3-methylimidazolium Methylphosphate, 1-Ethyl-3-methylimidazolium Diethylphosphate, 1-Butyl-3-methylimidazolium Acetate, and 1-Butyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)imide. J. Chem. Eng. Data 60, 876–885 (2015).
Jacquemin, J. et al. Prediction of Ionic Liquid Properties. I. Volumetric Properties as a Function of Temperature at 0.1 MPa. J. Chem. Eng. Data 53, 716–726 (2008).
Slattery, J. M., Daguenet, C., Dyson, P. J., Schubert, T. J. S. & Krossing, I. How to Predict the Physical Properties of Ionic Liquids: A Volume-Based Approach. Angew. Chemie Int. Ed. 46, 5384–5388 (2007).
Ye, C. & Shreeve, J. M. Rapid and Accurate Estimation of Densities of Room-Temperature Ionic Liquids and Salts. J. Phys. Chem. A 111, 1456–1461 (2007).
Gardas, R. L. & Coutinho, J. A. P. Extension of the Ye and Shreeve Group Contribution Method for Density Estimation of Ionic Liquids in a WideRange of Temperatures and Pressures. Fluid Phase Equilib 263, 26–32 (2008).
Lazzús, J. A. A Group Contribution Method to Predict ρ-T-P of Ionic Liquids. Chem. Eng. Commun. 197, 974–1015 (2010).
Qiao, Y., Ma, Y., Huo, Y., Ma, P. & Xia, S. A Group Contribution Method to Estimate the Densities of Ionic Liquids. J. Chem. Thermodyn. 42, 852–855 (2010).
Valderrama, J. O. & Zarricueta, K. A Simple and Generalized Model for Predicting the Density of Ionic Liquids. Fluid Phase Equilib 275, 145–151 (2009).
Paduszyński, K. & Domańska, U. A New Group Contribution Method For Prediction of Density of Pure Ionic Liquids over a Wide Range of Temperature and Pressure. Ind. Eng. Chem. Res. 51, 591–604 (2012).
Taherifard, H. & Raeissi, S. Estimation of the Densities of Ionic Liquids using a Group Contribution Method. J. Chem. Eng. Data 61, 4031–4038 (2016).
Abildskov, J., Ellegaard, M. D. & O’Connell, J. P. Densities and Isothermal Compressibilities of Ionic liquids—Modeling and Application. Fluid Phase Equilib 295, 215–229 (2010).
Shen, C., Li, C., Li, X., Lu, Y. & Muhammad, Y. Estimation of Densities of Ionic Liquids Using Patel–Teja Equation of State and Critical Properties Determined from Group Contribution Method. Chem. Eng. Sci. 66, 2690–2698 (2011).
Ji, X. & Adidharma, H. Thermodynamic Modeling of Ionic Liquid Density with Heterosegmented Statistical Associating Fluid Theory. Chem. Eng. Sci. 64, 1985–1992 (2009).
Wang, J., Li, Z., Li, C. & Wang, Z. Density Prediction of Ionic Liquids at Different Temperatures and Pressures Using a Group Contribution Equation of State Based on Electrolyte Perturbation Theory. Ind. Eng. Chem. Res. 49, 4420–4425 (2010).
Alavianmehr, M. M., Hosseini, S. M. & Moghadasi, J. Densities of Ionic Liquids from Ion Contribution-Based Equation of State: Electrolyte Perturbation Approach. J. Mol. Liq. 197, 287–294 (2014).
Lazzús, J. A. ρ(T, P) Model for Ionic Liquids Based on Quantitative Structure-Property Relationship Calculations. J. Phys. Org. Chem. 22, 1193–1197 (2009).
Trohalaki, S., Pachter, R., Drake, G. W. & Hawkins, T. Quantitative Structure−Property Relationships for Melting Points and Densities of Ionic Liquids. Energy Fuels 19, 279–284 (2005).
Palomar, J., Ferro, V. R., Torrecilla, J. S. & Rodríguez, F. Density and Molar Volume Predictions Using COSMO-RS for Ionic Liquids. An Approach to Solvent Design. Ind. Eng. Chem. Res. 46, 6041–6048 (2007).
Preiss, U. P. R. M., Slattery, J. M. & Krossing, I. In Silico Prediction of Molecular Volumes, Heat Capacities, and Temperature-Dependent Densities of Ionic Liquids. Ind. Eng. Chem. Res. 48, 2290–2296 (2009).
Lazzús, J. A. ρ–T–P Prediction for Ionic Liquids Using Neural Networks. J. Taiwan Inst. Chem. Eng. 40, 213–232 (2009).
Deetlefs, M., Seddon, K. R. & Shara, M. Predicting Physical Properties of Ionic Liquids. Phys. Chem. Chem. Phys. 8, 642–649 (2006).
Bandrés, I., Giner, B., Artigas, H., Royo, F. M. & Lafuente, C. Thermophysic Comparative Study of Two Isomeric Pyridinium-Based Ionic Liquids. J. Phys. Chem. B 112, 3077–3084 (2008).
Postnikov, E. B., Goncharov, A. L. & Melent’ev, V. V. Tait Equation Revisited from the Entropic and Fluctuational Points of View. Intern. J. Thermophys 35, 2115–2123 (2014).
Chorążewski, M. & Postnikov, E. B. Thermal Properties of Compressed Liquids: Experimental Determination via an Indirect Acoustic Technique and Modeling using the Volume Fluctuations Approach. Intern. J. Therm. Sci. 20, 62–69 (2015).
Chorążewski, M., Postnikov, E. B., Oster, K. & Polishuk, I. Thermodynamic Properties of 1,2-Dichloroethane and 1,2-Dibromoethane Under Elevated Pressures: Experimental Results and Predictions of a Novel DIPPR-Based Version of FT-EoS, PC-SAFT and CP-PC-SAFT. Ind. Eng. Chem. Res. 54, 9645–9656 (2015).
Postnikov, E. B., Goncharov, A. L., Cohen, N. & Polishuk, I. Estimating the Liquid Properties of 1-Alkanols from C5 to C12 by FT-EoS and CP-PC-SAFT: Simplicity Versus Complexity. J. Supercrit. Fluids 104, 193–203 (2015).
Landau, L. D. & Lifshitz, E. M. Theory of Elasticity. (Pergamon Press, Oxford, 1986).
Tait, P. G. Report on some Physical Properties of Fresh Water and of Sea Water. In.: Report on the Scientific Results of the Voyage of H.M.S. Challenger during the Years 1873-76. Physicsand Chemistry - Vol. II. (HM Stationary Office, 1889).
Tammann, G. Über die Abhängigkeit der Volumina von Lösungen vom Druck. Z. Phys. Chem. 17, 620–636 (1895).
Macdonald, J. R. Some Simple Isothermal Equations of State. Rev. Mod. Phys. 38, 669–679 (1966).
Murnaghan, F. D. The Compressibility of Media under Extreme Pressures. Proc. Natl. Acad. Sci. USA 30, 244–247 (1944).
Goncharov, A. L., Melent’ev, V. V. & Postnikov, E. B. Limits of Structure Stability of Simple Liquids Revealed by Study of Relative Fluctuations. Eur. Phys. J. B 86, 357 (2013).
Korotkovskii, V. I., Ryshkova, O. S., Neruchev, Y. A., Goncharov, A. L. & Postnikov, E. B. Isobaric Heat Capacity, Isothermal Compressibility and Fluctuational Properties of 1-Bromoalkanes. Intern. J. Thermophys 37, 1–12 (2016).
Fronczak, A. Microscopic Meaning of Grand Potential Resulting from Combinatorial Approach to a General System of Particles. Phys. Rev. E 86, 041139 (2012).
Postnikov, E. B. & Chorążewski, M. Transition in Fluctuation Behaviour of Normal Liquids Under High Pressures. Phys. A 449, 275–280 (2016).
Acknowledgements
M.Ch. is grateful for the financial support based on Decision No. 2016/23/B/ST8/02968 from the National Science Centre (Poland). J.J. acknowledges gratefully the CEA le Ripault (Grant No. 4600261677/P6E31) and the Engineering and Physical Sciences Research Council (EPSRC) for supporting this work financially (EPSRC First Grant Scheme, Grant No. EP/M021785/1); E.B.P. and Y.V.N. are supported by RFBR, research project No. 16-08-01203.
Author information
Authors and Affiliations
Contributions
M.Ch. proposed the concept, performed analytical calculations, designed and wrote the manuscript. E.B.P developed the theoretical model and wrote the manuscript. B.J. carried out analytical calculations and edited the manuscript. Y.V.N. wrote the VB Macro code for MS Excel. J.J. built the ILs database, checked the validity of the model with all selected ILs, and wrote the manuscript. All authors discussed and reviewed the whole manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Change History: A correction to this article has been published and is linked from the HTML version of this paper. The error has been fixed in the paper.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A correction to this article is available online at https://doi.org/10.1038/s41598-017-14855-2.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chorążewski, M., Postnikov, E.B., Jasiok, B. et al. A Fluctuation Equation of State for Prediction of High-Pressure Densities of Ionic Liquids. Sci Rep 7, 5563 (2017). https://doi.org/10.1038/s41598-017-06225-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-06225-9
This article is cited by
-
Combining the Tait equation with the phonon theory allows predicting the density of liquids up to the Gigapascal range
Scientific Reports (2023)
-
Thermal Conductivity of Ionic Liquids: Recent Challenges Facing Theory and Experiment
Journal of Solution Chemistry (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.