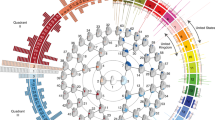
Abstract
Genome-wide association scans of complex multipartite traits like the human face typically use preselected phenotypic measures. Here we report a data-driven approach to phenotyping facial shape at multiple levels of organization, allowing for an open-ended description of facial variation while preserving statistical power. In a sample of 2,329 persons of European ancestry, we identified 38 loci, 15 of which replicated in an independent European sample (n = 1,719). Four loci were completely new. For the others, additional support (n = 9) or pleiotropic effects (n = 2) were found in the literature, but the results reported here were further refined. All 15 replicated loci highlighted distinctive patterns of global-to-local genetic effects on facial shape and showed enrichment for active chromatin elements in human cranial neural crest cells, suggesting an early developmental origin of the facial variation captured. These results have implications for studies of facial genetics and other complex morphological traits.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Roosenboom, J., Hens, G., Mattern, B. C., Shriver, M. D. & Claes, P. Exploring the underlying genetics of craniofacial morphology through various sources of knowledge. BioMed Res. Int. 2016, 3054578 (2016).
Paternoster, L. et al. Genome-wide association study of three-dimensional facial morphology identifies a variant in PAX3 associated with nasion position. Am. J. Hum. Genet. 90, 478–485 (2012).
Liu, F. et al. A genome-wide association study identifies five loci influencing facial morphology in Europeans. PLoS Genet. 8, e1002932 (2012).
Adhikari, K. et al. A genome-wide association scan implicates DCHS2, RUNX2, GLI3, PAX1 and EDAR in human facial variation. Nat. Commun. 7, 11616 (2016).
Cole, J. B. et al. Genomewide association study of African children identifies association of SCHIP1 and PDE8A with facial size and shape. PLoS Genet. 12, e1006174 (2016).
Shaffer, J. R. et al. Genome-wide association study reveals multiple loci influencing normal human facial morphology. PLoS Genet. 12, e1006149 (2016).
Lee, M. K. et al. Genome-wide association study of facial morphology reveals novel associations with FREM1 and PARK2. PLoS One 12, e0176566 (2017).
Abecasis, G. R. et al. An integrated map of genetic variation from 1,092 human genomes. Nature 491, 56–65 (2012).
Snyders, J., Claes, P., Vandermeulen, D. & Suetens, P. Development and comparison of non-rigid surface registration and extensions (technical report KUL/ESAT/PSI/1401) 1–55 (2014).
Claes, P. et al. Modeling 3D facial shape from DNA. PLoS Genet. 10, e1004224 (2014).
Ng, A. Y., Jordan, M. I. & Weiss, Y. On spectral clustering: analysis and an algorithm. in Proc. 14th International Conference Neural Information Processing Systems: Natural and Synthetic 849–856 (MIT Press, Cambridge, MA, 2001).
Hayton, J. C., Allen, D. G. & Scarpello, V. Factor retention decisions in exploratory factor analysis: a tutorial on parallel analysis. Organ. Res. Methods 7, 191–205 (2004).
Thompson, B. Canonical correlation analysis. in Encyclopedia of Statistics in Behavioral Science (eds. Everitt, B. & Howell, D.) (John Wiley and Sons, Hoboken, NJ, 2005).
Benjamini, Y. & Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 29, 1165–1188 (2001).
McLean, C. Y. et al. GREAT improves functional interpretation of cis-regulatory regions. Nat. Biotechnol. 28, 495–501 (2010).
Bronner, M. E. & LeDouarin, N. M. Development and evolution of the neural crest: an overview. Dev. Biol. 366, 2–9 (2012).
Green, S. A., Simoes-Costa, M. & Bronner, M. E. Evolution of vertebrates as viewed from the crest. Nature 520, 474–482 (2015).
Schneider, R. A. Regulation of jaw length during development, disease, and evolution. Curr. Top. Dev. Biol. 115, 271–298 (2015).
Cordero, D. R. et al. Cranial neural crest cells on the move: their roles in craniofacial development. Am. J. Med. Genet. A 155A, 270–279 (2011).
Kulesa, P. M. & McLennan, R. Neural crest migration: trailblazing ahead. F1000Prime Rep. 7, 02 (2015).
Prescott, S. L. et al. Enhancer divergence and cis-regulatory evolution in the human and chimp neural crest. Cell 163, 68–83 (2015).
Rada-Iglesias, A. et al. Epigenomic annotation of enhancers predicts transcriptional regulators of human neural crest. Cell Stem Cell 11, 633–648 (2012).
Rada-Iglesias, A. et al. A unique chromatin signature uncovers early developmental enhancers in humans. Nature 470, 279–283 (2011).
Creyghton, M. P. et al. Histone H3K27ac separates active from poised enhancers and predicts developmental state. Proc. Natl. Acad. Sci. USA 107, 21931–21936 (2010).
Tak, Y. G. & Farnham, P. J. Making sense of GWAS: using epigenomics and genome engineering to understand the functional relevance of SNPs in non-coding regions of the human genome. Epigenetics Chromatin 8, 57 (2015).
Long, H. K., Prescott, S. L. & Wysocka, J. Ever-changing landscapes: transcriptional enhancers in development and evolution. Cell 167, 1170–1187 (2016).
Corradin, O. & Scacheri, P. C. Enhancer variants: evaluating functions in common disease. Genome Med. 6, 85 (2014).
Ludwig, K. U. et al. Imputation of orofacial clefting data identifies novel risk loci and sheds light on the genetic background of cleft lip ± cleft palate and cleft palate only. Hum. Mol. Genet. 26, 829–842 (2017).
Staley, J. R. et al. PhenoScanner: a database of human genotype–phenotype associations. Bioinformatics 32, 3207–3209 (2016).
Pickrell, J. K. et al. Detection and interpretation of shared genetic influences on 42 human traits. Nat. Genet. 48, 709–717 (2016).
Klingenberg, C. P. Quantitative genetics of geometric shape: heritability and the pitfalls of the univariate approach. Evolution 57, 191–195 (2003).
Pallares, L. F. et al. Mapping of craniofacial traits in outbred mice identifies major developmental genes involved in shape determination. PLoS Genet. 11, e1005607 (2015).
Maga, A. M., Navarro, N., Cunningham, M. L. & Cox, T. C. Quantitative trait loci affecting the 3D skull shape and size in mouse and prioritization of candidate genes in-silico. Front. Physiol. 6, 92 (2015).
Coussens, A. K. & van Daal, A. Linkage disequilibrium analysis identifies an FGFR1 haplotype-tag SNP associated with normal variation in craniofacial shape. Genomics 85, 563–573 (2005).
Peng, S. et al. Detecting genetic association of common human facial morphological variation using high density 3D image registration. PLoS Comput. Biol. 9, e1003375 (2013).
Carlson, D. S. Theories of craniofacial growth in the postgenomic era. Semin. Orthod. 11, 172–183 (2005).
Sperber, G. H., Guttmann, G. D. & Sperber, S. M. Craniofacial Development (Book for Windows & Macintosh) (PMPH-USA, Hamilton-London, 2001).
Williams, S. E. & Slice, D. E. Regional shape change in adult facial bone curvature with age. Am. J. Phys. Anthropol. 143, 437–447 (2010).
Mitteroecker, P. & Bookstein, F. The evolutionary role of modularity and integration in the hominoid cranium. Evolution 62, 943–958 (2008).
Klingenberg, C. P. Morphological integration and developmental modularity. Annu. Rev. Ecol. Evol. Syst. 39, 115–132 (2008).
Wood, A. R. et al. Defining the role of common variation in the genomic and biological architecture of adult human height. Nat. Genet. 46, 1173–1186 (2014).
Zarelli, V. E. & Dawid, I. B. Inhibition of neural crest formation by Kctd15 involves regulation of transcription factor AP-2. Proc. Natl. Acad. Sci. USA 110, 2870–2875 (2013).
Ahituv, N. et al. An ENU-induced mutation in AP-2α leads to middle ear and ocular defects in Doarad mice. Mamm. Genome 15, 424–432 (2004).
Lee, Y. H. & Saint-Jeannet, J. P. Sox9 function in craniofacial development and disease. Genesis 49, 200–208 (2011).
Francis-West, P. H., Robson, L. & Evans, D. J. Craniofacial Development: The Tissue and Molecular Interactions Tha t Control Development of the Head (Springer Science & Business Media, Berlin-Heidelberg, 2012).
Stearns, F. W. One hundred years of pleiotropy: a retrospective. Genetics 186, 767–773 (2010).
Boyle, E. A., Li, Y. I. & Pritchard, J. K. An expanded view of complex traits: from polygenic to omnigenic. Cell 169, 1177–1186 (2017).
Weinberg, S. M. et al. The 3D Facial Norms Database: Part 1. A web-based craniofacial anthropometric and image repository for the clinical and research community. Cleft Palate Craniofac. J. 53, e185–e197 (2016).
Heike, C. L., Upson, K., Stuhaug, E. & Weinberg, S. M. 3D digital stereophotogrammetry: a practical guide to facial image acquisition. Head Face Med. 6, 18 (2010).
Claes, P., Walters, M. & Clement, J. Improved facial outcome assessment using a 3D anthropometric mask. Int. J. Oral Maxillofac. Surg. 41, 324–330 (2012).
Claes, P., Walters, M., Vandermeulen, D. & Clement, J. G. Spatially-dense 3D facial asymmetry assessment in both typical and disordered growth. J. Anat. 219, 444–455 (2011).
Rohlf, F. & Slice, D. Extensions of the procrustus method for the optimal superimposition of landmarks. Syst. Zool. 39, 40–59 (1990).
Robert, P. & Escoufier, Y. A unifying tool for linear multivariate statistical methods: the RV-coefficient. Appl. Stat. 25, 257–265 (1976).
Laurie, C. C. et al. Quality control and quality assurance in genotypic data for genome-wide association studies. Genet. Epidemiol. 34, 591–602 (2010).
Delaneau, O., Zagury, J.-F. & Marchini, J. Improved whole-chromosome phasing for disease and population genetic studies. Nat. Methods 10, 5–6 (2013).
Howie, B. N., Donnelly, P. & Marchini, J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 5, e1000529 (2009).
Howie, B., Marchini, J. & Stephens, M. Genotype imputation with thousands of genomes. G3 1, 457–470 (2011).
Alexander, D. H., Novembre, J. & Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 19, 1655–1664 (2009).
Purcell, S. et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575 (2007).
Olson, C. L. On choosing a test statistic in multivariate analysis of variance. Psychol. Bull. 83, 579 (1976).
Pe’er, I., Yelensky, R., Altshuler, D. & Daly, M. J. Estimation of the multiple testing burden for genomewide association studies of nearly all common variants. Genet. Epidemiol. 32, 381–385 (2008).
Li, J. & Ji, L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlation matrix. Heredity 95, 221–227 (2005).
Valouev, A. et al. Genome-wide analysis of transcription factor binding sites based on ChIP-Seq data. Nat. Methods 5, 829–834 (2008).
Acknowledgements
This investigation was supported by KU Leuven, BOF funds GOA, CREA and C1. The collaborators at the University of Pittsburgh were supported by the National Institute for Dental and Craniofacial Research (see URLs) through the following grants: U01-DE020078, U01-DE020057, R01-DE016148, K99-DE02560 and 1-R01-DE027023. Funding for genotyping was provided by the National Human Genome Research Institute (see URLs): X01-HG007821 and X01-HG007485. Funding for initial genomic data cleaning by the University of Washington was provided by contract HHSN268201200008I from the National Institute for Dental and Craniofacial Research (see URLs) awarded to the Center for Inherited Disease Research (CIDR). The collaborators at Penn State University were supported in part by grants from the Center for Human Evolution and Development at Penn State, the Science Foundation of Ireland Walton Fellowship (04.W4/B643), the US National Institute of Justice (see URLs; 2008-DN-BX-K125) and the US Department of Defense (see URLs). The collaborators at the Stanford University School of Medicine were supported by the Howard Hughes Medical Institute, NIH U01 DE024430 and the March of Dimes Foundation 1-FY15-312 (J.W.). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Author information
Authors and Affiliations
Contributions
This work is the result of a four-center collaboration between KU Leuven, the University of Pittsburgh, Penn State University and the Stanford University School of Medicine, led by P.C., S.M.W., M.D.S. and J.W., respectively. All four centers contributed equally to this work. P.C. and D.S. with input from P.S. and D.V. conceptualized and implemented the global-to-local facial segmentations. J.L. provided genomic data support and analysis at the KU Leuven site and together with P.C. ran the GWAS. M.K.L., J.R., E.J.L., J.C.C., E.O., E.F., M.L.M., J.R.S. and S.M.W. organized the PITT cohort and co-analyzed the GWAS results, generated LocusZoom plots and organized the results into 38 loci. J.D.W., A.Z., B.C.M., C.L., L.P., T.G. and M.D.S. organized the PSU cohort, imputed the PSU genetic data and co-analyzed the GWAS results. T.S. and J.W. performed the GREAT analysis and the association with CNCCs. P.C. wrote the manuscript with extensive input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1 Hierarchical spectral clustering on the PSU cohort
A global-to-local facial segmentation of the PSU cohort obtained using hierarchical spectral clustering. Note that the order of quadrants, or facial segments at each level, is not necessarily the same as for Fig. 1, on the PITT cohort. The reason is the randomness in the clustering that does not preserve such order and hence the use of the normalized mutual information as a measure of overlap.
Supplementary Figure 2 Biological shape variables per facial segment
Left, the number of principal components retained after parallel analysis for each facial segment. Right, the amount of variation explained by the principal components expressed as percentage for each facial segment.
Supplementary Figure 3 GREAT analysis GREAT GO gene ontology analysis results for the 15 top replicated SNPs in
Table 1. Plotted is the binomial test FDR (cyan) and binomial enrichment (magenta) for indicated top associated biological processes, phenotypes and expression pattern categories.
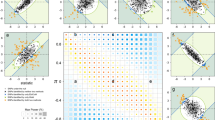
Supplementary Figure 4 Statistical replication result for rs2045323
a, –log10 (P value) of the canonical correlation per facial segment ranging from 0 to –log10 (8.01 × 10–5), i.e., the Bonferroni-corrected P value for literature replication. Black-encircled facial segments have reached nominal replication (P = 0.05). b, The canonical correlation [0 1]. c, The normal displacement (displacement in the direction locally normal to the facial surface) in each quasi-landmark of facial segment 45 going from the major to the minor allele SNP variant. Blue, inward depression; red, outward protrusion.
Supplementary Figure 5 Statistical discovery result for rs2424390
a, –log10 (P value) of the canonical correlation per facial segment ranging from 0 to –log10 (1.28 × 10–9), i.e., the Bonferroni-corrected P value for discovery. Black-encircled facial segments have reached nominal genome-wide significance (P ≤ 5 × 10–8). b, The canonical correlation [0 1]. c, The normal displacement (displacement in the direction locally normal to the facial surface) in each quasi-landmark of facial segment 11, going from the major to the minor allele SNP variant. Blue, inward depression; red, outward protrusion.
Supplementary Figure 6 Two loci associated with different aspects of nasal shape
a, 6p21.1 locus with peak SNP rs227833 and candidate gene SUPT3H. b, 19q13.11 locus with peak SNP rs287104 and candidate gene KCTD15. The locus in a is primarily affecting the nasal bridge and ridge, leaving the nose tip unaffected. The locus in b is focused on the nose tip only, which could indicate potentially different underlying soft tissue regulations. Top, –log10 (P value) of the canonical correlation per facial segment ranging from 0 to –log10 (1.28 × 10–9), i.e., the Bonferroni-corrected P value for discovery. Bottom, the normal displacement (displacement in the direction locally normal to the facial surface) in each quasi-landmark of a representative facial segment per locus, going from the major to the minor allele SNP variant. Blue, inward depression; red, outward protrusion.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–6, Supplementary Tables 1–7 and Supplementary Notes 1 and 2
Rights and permissions
About this article
Cite this article
Claes, P., Roosenboom, J., White, J.D. et al. Genome-wide mapping of global-to-local genetic effects on human facial shape. Nat Genet 50, 414–423 (2018). https://doi.org/10.1038/s41588-018-0057-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41588-018-0057-4
This article is cited by
-
Craniofacial syndromes and class III phenotype: common genotype fingerprints? A scoping review and meta-analysis
Pediatric Research (2024)
-
Sentinel cells programmed to respond to environmental DNA including human sequences
Nature Chemical Biology (2024)
-
De Novo Dissecting the Three-Dimensional Facial Morphology of 2379 Han Chinese Individuals
Phenomics (2024)
-
Integrative analysis of transcriptome dynamics during human craniofacial development identifies candidate disease genes
Nature Communications (2023)
-
Precise modulation of transcription factor levels identifies features underlying dosage sensitivity
Nature Genetics (2023)