Abstract
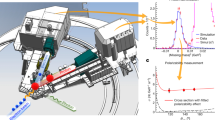
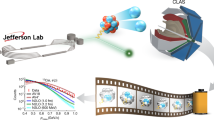
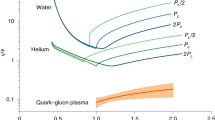
The proton, one of the components of atomic nuclei, is composed of fundamental particles called quarks and gluons. Gluons are the carriers of the force that binds quarks together, and free quarks are never found in isolation—that is, they are confined within the composite particles in which they reside. The origin of quark confinement is one of the most important questions in modern particle and nuclear physics because confinement is at the core of what makes the proton a stable particle and thus provides stability to the Universe. The internal quark structure of the proton is revealed by deeply virtual Compton scattering1,2, a process in which electrons are scattered off quarks inside the protons, which subsequently emit high-energy photons, which are detected in coincidence with the scattered electrons and recoil protons. Here we report a measurement of the pressure distribution experienced by the quarks in the proton. We find a strong repulsive pressure near the centre of the proton (up to 0.6 femtometres) and a binding pressure at greater distances. The average peak pressure near the centre is about 1035 pascals, which exceeds the pressure estimated for the most densely packed known objects in the Universe, neutron stars3. This work opens up a new area of research on the fundamental gravitational properties of protons, neutrons and nuclei, which can provide access to their physical radii, the internal shear forces acting on the quarks and their pressure distributions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Ji, X. D. Deeply virtual Compton scattering. Phys. Rev. D 55, 7114–7125 (1997).
Ji, X. D. Gauge-invariant decomposition of nucleon spin. Phys. Rev. Lett. 78, 610–613 (1997).
Ozel, F. & Freire, P. Masses, radii, and equation of state of neutron stars. Annu. Rev. Astron. Astrophys. 54, 401–440 (2016).
Pagels, H. Energy–momentum structure form factors of particles. Phys. Rev. 144, 1250–1260 (1966).
Teryaev, O. V. Gravitational form factors and nucleon spin structure. Front. Phys. 11, 111207 (2016).
Belitsky, A. V. & Radyushkin, A. V. Unraveling hadron structure with generalized parton distributions. Phys. Rep. 418, 1–387 (2005).
Müller, D., Robaschik, D., Geyer, D., Dittes, F. M. & Horejši, J. Wave functions, evolution equations and evolution kernels from light-ray operators of QCD. Fortschr. Phys. 42, 101–141 (1994).
Radyushkin, A. V. Scaling limit of deeply virtual Compton scattering. Phys. Lett. B 380, 417–425 (1996).
Polyakov, M. V. Generalized parton distributions and strong forces inside nucleons and nuclei. Phys. Lett. B 555, 57–62 (2003).
Kumericˇ ki, K. & Müller, D. Deeply virtual Compton scattering at small x B and the access to the GPD H. Nucl. Phys. B 841, 1–58 (2010).
Müller, D., Lautenschlager, T., Passek-Kumericki, K. & Schaefer, A. Towards a fitting procedure to deeply virtual meson production – the next-to-leading order case. Nucl. Phys. B 884, 438–546 (2014).
Guidal, M., Moutarde, H. & Vanderhaeghen, M. Generalized parton distributions in the valence region from deeply virtual Compton scattering. Rep. Prog. Phys. 76, 066202 (2013).
Kumericˇ ki, K., Liuti, S. & Moutarde, H. GPD phenomenology and DVCS fitting: entering the high-precision era. Eur. Phys. J. A 52, 157 (2016).
Diehl, M. & Ivanov, D. Y. Dispersion representations for hard exclusive processes: beyond the Born approximation. Eur. Phys. J. C 52, 919–932 (2007).
Anikin, I. V. & Teryaev, O. V. Dispersion relations and QCD factorization in hard reactions. Fizika B 17, 151–158 (2008).
Pasquini, B., Polyakov, M. V. & Vanderhaeghen, M. Dispersive evaluation of the D-term form factor in deeply virtual Compton scattering. Phys. Lett. B 739, 133–138 (2014).
Polyakov, M. V. & Weiss, C. Skewed and double distributions in the pion and the nucleon. Phys. Rev. D 60, 114017 (1999).
Radyushkin, A. V. Modeling nucleon generalized parton distributions. Phys. Rev. D 87, 096017 (2013).
Radyushkin, A. V. Sum rules for nucleon generalized parton distributions and border function formulation. Phys. Rev. D 88, 056010 (2013).
Lepage, G. P. & Brodsky, S. J. Exclusive processes in perturbative quantum chromodynamics. Phys. Rev. D 22, 2157–2198 (1980).
CLAS Collaboration. Measurement of deeply virtual Compton scattering beam-spin asymmetries. Phys. Rev. Lett. 100, 162002 (2008).
CLAS Collaboration. Cross sections for the exclusive photon electroproduction on the proton and generalized parton distributions. Phys. Rev. Lett. 115, 212003 (2015).
Kim, H. C., Schweitzer, P. & Yakhshiev, U. Energy–momentum tensor form factors of the nucleon in nuclear matter. Phys. Lett. B 718, 625–631 (2012).
Goeke, K. et al. Nucleon form factors of the energy–momentum tensor in the chiral quark–soliton model. Phys. Rev. D 75, 094021 (2007).
Kivel, N., Polyakov, M. V. & Vanderhaeghen, M. Deeply virtual Compton scattering on the nucleon: study of the twist-3 effects. Phys. Rev. D 63, 114014 (2001).
Eides, M. I., Petrov, V. Y. & Polyakov, M. V. Narrow nucleon–ψ(2S) bound state and LHCb pentaquarks. Phys. Rev. D 93, 054039 (2016).
Jung, J. H., Yakhshiev, U., Kim, H. C. & Schweitzer, P. In-medium modified energy–momentum tensor form factors of the nucleon within the framework of a π–ρ–ω soliton model. Phys. Rev. D 89, 114021 (2014).
Perevalova, I. A., Polyakov, M. V. & Schweitzer, P. LHCb pentaquarks as a baryon–ψ(2S) bound state: prediction of isospin-3/2 pentaquarks with hidden charm. Phys. Rev. D 94, 054024 (2016).
Hudson, J. & Schweitzer, P. D term and the structure of pointlike and composed spin-0 particles. Phys. Rev. D 96, 114013 (2017).
CLAS Collaboration Deeply Virtual Compton Scattering with CLAS12 at 6.6 GeV and 8.8 GeV. Proposal E12–16–010B (Jefferson Lab PAC44, 2016); https://www.jlab.org/exp_prog/proposals/16/PR12-16-010B.pdf.
Acknowledgements
We thank M. Polyakov and P. Schweitzer for discussions on the subject matter of this work. We are indebted to G. D. Cates for reading the manuscript and suggesting text improvements. This material is based on work supported by the US Department of Energy, Office of Science, Office of Nuclear Physics under contract DE-AC05-06OR23177.
Reviewer information
Nature thanks G. D. Cates and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
V.D.B. wrote the manuscript initiated the analysis, and coordinated and oversaw the research and the validation of the results. L.E. worked with theory experts on the feasibility of the present analysis to develop a procedure connecting the data to the pressure measurements and worked on the analysis of the DVCS beam spin asymmetry. F.X.G. provided the detailed analysis of beam asymmetry and the cross-section measurements, performed the fits to extract the D-term and used the dispersion relation analysis to relate the results to the confinement form factor d1(t).
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Compton form factor \(\pmb{\mathscr{H}}\) at −t = 0.15 GeV2.
The graphs show the imaginary (left) and real (right) parts of \({\mathscr{H}}\) versus the momentum transfer to the quark, ξ. The inner red curve shows the result of our global fit. The grey band shows the estimated uncertainties from the contributions of other CFFs, the outer red band shows the total uncertainties of the imaginary part of the amplitude, and the outer blue band (right) includes the uncertainties related to the D-term. All uncertainties represent one standard deviation.
Extended Data Fig. 2 Compton form factor \(\pmb{\mathscr{H}}\) at −t = 0.11 GeV2 and at −t = 0.20 GeV2.
The imaginary (left) and real (right) parts of \({\mathscr{H}}\) are shown as a function of ξ. The red curve and the grey, red and blue bands are as in Extended Data Fig. 1. All uncertainties represent one standard deviation.
Extended Data Fig. 3 Compton form factor \(\pmb{\mathscr{H}}\) at −t = 0.26 GeV2 and at −t = 0.34 GeV2.
The imaginary (left) and real (right) parts of \({\mathscr{H}}\) are shown as a function of ξ. The red curve and the grey, red and blue bands are as in Extended Data Fig. 1. All uncertainties represent one standard deviation.
Rights and permissions
About this article
Cite this article
Burkert, V.D., Elouadrhiri, L. & Girod, F.X. The pressure distribution inside the proton. Nature 557, 396–399 (2018). https://doi.org/10.1038/s41586-018-0060-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0060-z
This article is cited by
-
Gravitational p → ∆+ transition form factors in chiral perturbation theory
Journal of High Energy Physics (2024)
-
Gravitational form factors of a kink in 1 + 1 dimensional ϕ4 model
Journal of High Energy Physics (2023)
-
Twist-four gravitational form factor at NNLO QCD from trace anomaly constraints
Journal of High Energy Physics (2023)
-
Gravitational transition form factors of N → ∆ via QCD light-cone sum rules
Journal of High Energy Physics (2023)
-
Status on lattice calculations of the proton spin decomposition
AAPPS Bulletin (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.