Abstract
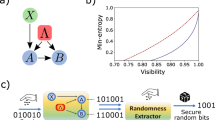
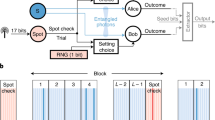
From dice to modern electronic circuits, there have been many attempts to build better devices to generate random numbers. Randomness is fundamental to security and cryptographic systems and to safeguarding privacy. A key challenge with random-number generators is that it is hard to ensure that their outputs are unpredictable1,2,3. For a random-number generator based on a physical process, such as a noisy classical system or an elementary quantum measurement, a detailed model that describes the underlying physics is necessary to assert unpredictability. Imperfections in the model compromise the integrity of the device. However, it is possible to exploit the phenomenon of quantum non-locality with a loophole-free Bell test to build a random-number generator that can produce output that is unpredictable to any adversary that is limited only by general physical principles, such as special relativity1,2,3,4,5,6,7,8,9,10,11. With recent technological developments, it is now possible to carry out such a loophole-free Bell test12,13,14,22. Here we present certified randomness obtained from a photonic Bell experiment and extract 1,024 random bits that are uniformly distributed to within 10−12. These random bits could not have been predicted according to any physical theory that prohibits faster-than-light (superluminal) signalling and that allows independent measurement choices. To certify and quantify the randomness, we describe a protocol that is optimized for devices that are characterized by a low per-trial violation of Bell inequalities. Future random-number generators based on loophole-free Bell tests may have a role in increasing the security and trust of our cryptographic systems and infrastructure.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Acín, A. & Masanes, L. Certified randomness in quantum physics. Nature 540, 213–219 (2016).
Pironio, S. & Massar, S. Security of practical private randomness generation. Phys. Rev. A 87, 012336 (2013).
Miller, C. A. & Shi, Y. Robust protocols for securely expanding randomness and distributing keys using untrusted quantum devices. J. ACM 63, 33 (2016).
Colbeck, R. & Kent, A. Private randomness expansion with untrusted devices. J. Phys. A 44, 095305 (2011).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).
Vazirani, U. & Vidick, T. Certifiable quantum dice - or, exponential randomness expansion. In STOC’12 Proc. 44th Annual ACM Symposium on Theory of Computing (ed. Pitassi, T.) 61–76 (2012).
Fehr, S., Gelles, R. & Schaffner, C. Security and composability of randomness expansion from Bell inequalities. Phys. Rev. A 87, 012335 (2013).
Chung, K.-M., Shi, Y. & Wu, X. Physical randomness extractors: generating random numbers with minimal assumptions. Preprint at https://arxiv.org/abs/1402.4797 (2014).
Nieto-Silleras, O., Pironio, S. & Silman, J. Using complete measurement statistics for optimal device-independent randomness evaluation. New J. Phys. 16, 013035 (2014).
Bancal, J.-D., Sheridan, L. & Scarani, V. More randomness from the same data. New J. Phys. 16, 033011 (2014).
Thinh, L., de la Torre, G., Bancal, J.-D., Pironio, P. & Scarani, V. Randomness in post-selected events. New J. Phys. 18, 035007 (2016).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism. Phys. Rev. Lett. 115, 250402 (2015).
Giustina, M. et al. Significant-loophole-free test of Bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Paar, C. & Pelzl, J. Understanding Cryptography (Springer, Heidelberg, 2010).
Fischer, M. J., Iorga, M. & Peralta, R. A public randomness service. In Proc. International Conference on Security and Cryptography (SECRYPT 2011) (eds Lopez, J. & Samarati, P.) 434–438 (2011).
Bell, J. S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1, 195–200 (1964).
Bell, J. S., Shimony, A., Horne, M. A. & Clauser, J. F. An exchange on local beables. Dialectica 39, 85–96 (1985).
Mayers, D. & Yao, A. Quantum cryptography with imperfect apparatus. In FOCS’98 Proc. 39th Annual Symposium on Foundations of Computer Science (ed Motwani, R.) 503–509 (1998).
Acín, A. et al. Device-independent security of quantum cryptography against collective attacks. Phys. Rev. Lett. 98, 230501 (2007).
Liu, Y. et al. High-speed device-independent quantum random number generation without a detection loophole. Phys. Rev. Lett. 120, 010503 (2018).
Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).
Abellán, C. et al. Challenging local realism with human choices. Nature (in the press).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Cirel’son, B. S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 4, 93–100 (1980).
Navascués, M., Pironio, S. & Acín, A. A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations. New J. Phys. 10, 073013 (2008).
Trevisan, L. Extractors and pseudorandom generators. J. Assoc. Comput. Mach. 48, 860–879 (2001).
Mauerer, W., Portmann, C. & Scholz, V. B. A modular framework for randomness extraction based on Trevisan’s construction. Preprint at https://arxiv.org/abs/1212.0520 (2012).
Coudron, M. & Yuen, H. Infinite randomness expansion with a constant number of devices. In STOC’14 Proc. 46th Annual ACM Symposium on Theory of Computing (ed Shmoys, D.) 427–436 (2014).
Arnon-Friedman, R., Dupuis, F., Fawzi, O., Renner, R. & Vidick, T. Practical device-independent quantum cryptography via entropy accumulation. Nat. Commun. 9, 459 (2018).
Miller, C. & Shi, Y. Universal security for randomness expansion from the spot-checking protocol. SIAM J. Comput. 46, 1304–1335 (2017).
Zhang, Y., Glancy, S. & Knill, E. Asymptotically optimal data analysis for rejecting local realism. Phys. Rev. A 84, 062118 (2011).
Marsili, F. et al. Detecting single infrared photons with 93% system efficiency. Nat. Photon. 7, 210–214 (2013).
Acknowledgements
We thank C. Miller and K. Coakley for comments on the manuscript. A.M. acknowledges financial support through NIST grant 70NANB16H207. This work is a contribution of the National Institute of Standards and Technology and is not subject to US copyright.
Reviewer information
Nature thanks S. Pironio and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
P.B. led the project and implemented the protocol. P.B., E.K., S.G. and Y.Z. developed the protocol theory. A.M., S.J., A.R. and Y.-K.L. were responsible for the extractor theory and implementation. B.C., S.W.N., M.J.S. and L.K.S. collected and interpreted the data. P.B., E.K., S.G. and L.K.S. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains a Supplementary Discussion, Supplementary Tables 1-6, Supplementary Equations and Supplementary References. It includes the proofs of the Entropy Production Theorem and the Protocol Soundness Theorem. It also describes how we choose the Bell function T, the implementation of the randomness extraction algorithm, details of how we analyzed the data, and comparisons to other implementations. It includes six tables S1-S6: S1 “Protocol for randomness generation,” S2 “Result counts,” S3 “Maximum likelihood non-signaling distribution,” S4 “Bell function T” (with legend), S5 “Summary of application of protocol to data sets” (with legend), and S6 “2-tail p-values for consistency checks.”.
Rights and permissions
About this article
Cite this article
Bierhorst, P., Knill, E., Glancy, S. et al. Experimentally generated randomness certified by the impossibility of superluminal signals. Nature 556, 223–226 (2018). https://doi.org/10.1038/s41586-018-0019-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0019-0
This article is cited by
-
Semi-device-independent quantum random number generator with a broadband squeezed state of light
npj Quantum Information (2024)
-
Quantum random number generation based on a perovskite light emitting diode
Communications Physics (2023)
-
A comprehensive review of quantum random number generators: concepts, classification and the origin of randomness
Quantum Information Processing (2023)
-
On the condition of Setting Independence
European Journal for Philosophy of Science (2023)
-
Random World and Quantum Mechanics
Foundations of Science (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.