Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Capturing the continuous complexity of behaviour in Caenorhabditis elegans

Nature Physics volume 17, pages 275–283 (2021)Cite this article

Subjects

Abstract

Animal behaviour is often quantified through subjective, incomplete variables that mask essential dynamics. Here, we develop a maximally predictive behavioural-state space from multivariate measurements, in which the full instantaneous state is smoothly unfolded as a combination of short-time posture sequences. In the off-food behaviour of the roundworm Caenorhabditis elegans, we discover a low-dimensional state space dominated by three sets of cyclic trajectories corresponding to the worm’s basic stereotyped motifs: forward, backward and turning locomotion. We find similar results in the on-food behaviour of foraging worms and npr-1 mutants. In contrast to this broad stereotypy, we find variability in the presence of locally unstable dynamics with signatures of deterministic chaos: a collection of unstable periodic orbits together with a positive maximal Lyapunov exponent. The full Lyapunov spectrum is symmetric with positive, chaotic exponents driving variability balanced by negative, dissipative exponents driving stereotypy. The symmetry is indicative of damped–driven Hamiltonian dynamics underlying the worm’s movement control.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: State-space reconstruction.
Fig. 2: Reconstruction parameters for maximum predictability.
Fig. 3: The low-dimensional state space of C. elegans locomotion.
Fig. 4: Chaotic state-space dynamics reveal a deterministic component of behavioural variability.
Fig. 5: A symmetric Lyapunov spectrum indicates damped–driven Hamiltonian dynamics.

Similar content being viewed by others

Data availability

Posture-mode time series for all worms analysed here are publicly available: https://bitbucket.org/tosifahamed/behavioral-state-space. Original image data for the foraging and escape-response datasets were analysed previously37 and are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.t0m6p. Data for N2 worms on food and npr-1 mutants were collected from an open-access dataset84 and analysed to solve for coiled postures11. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Code availability

Code for all analysis reported here was written in MATLAB83 and is publicly available: https://bitbucket.org/tosifahamed/behavioral-state-space.

References

  1. Berman, G. J. Measuring behavior across scales. BMC Biol. 16, 23 (2018).

    Google Scholar 

  2. Newell, K. & Corcos, D. Variability and Motor Control (Human Kinetics, 1993); https://books.google.co.jp/books?id=gUgQAQAAMAAJ

  3. Maye, A., Hsieh, C.-h, Sugihara, G. & Brembs, B. Order in spontaneous behavior. PloS ONE 2, e443 (2007).

    ADS  Google Scholar 

  4. Moore, T. Y., Cooper, K. L., Biewener, A. A. & Vasudevan, R. Unpredictability of escape trajectory explains predator evasion ability and microhabitat preference of desert rodents. Nat. Commun. 8, 440 (2017).

  5. Krakauer, J. W., Ghazanfar, A. A., Gomez-Marin, A., MacIver, M. A. & Poeppel, D. Neuroscience needs behavior: correcting a reductionist bias. Neuron 93, 480–490 (2017).

    Google Scholar 

  6. Cowan, N. J. et al. Feedback control as a framework for understanding tradeoffs in biology. Am. Zool. 54, 223–237 (2014).

    Google Scholar 

  7. Aguilar, J. et al. A review on locomotion robophysics: the study of movement at the intersection of robotics, soft matter and dynamical systems. Rep. Prog. Phys. 79, 110001 (2016).

    ADS  Google Scholar 

  8. Brown, A. E. X. & de Bivort, B. Ethology as a physical science. Nat. Phys. 14, 653–657 (2018).

    Google Scholar 

  9. Alexander, M. et al. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 21, 1281–1289 (2018).

    Google Scholar 

  10. Talmo D, P. et al. Fast animal pose estimation using deep neural networks. Nat. Methods 16, 117–125 (2019).

    Google Scholar 

  11. Hebert, L., Ahamed, T., Costa, A. C., O’Shaughnessy, L. & Stephens, G. J. WormPose: image synthesis and convolutional networks for pose estimation in C. elegans. Preprint at https://www.biorxiv.org/content/early/2020/07/10/2020.07.09.193755 (2020).

  12. Graving, J. M. et al. DeepPoseKit: a software toolkit for fast and robust animal pose estimation using deep learning. eLife 8, e47994 (2019).

    Google Scholar 

  13. Wiltschko, A. B. et al. Mapping sub-second structure in mouse behavior. Neuron 88, 1121–1135 (2015).

    Google Scholar 

  14. Berman, G. J., Choi, D. M., Bialek, W. & Shaevitz, J. W. Mapping the stereotyped behaviour of freely moving fruit flies. J. R. Soc. Interface 11, 20140672–12 (2014).

    Google Scholar 

  15. Stephens, G. J., Johnson-Kerner, B., Bialek, W. & Ryu, W. S. Dimensionality and dynamics in the behavior of C. elegans. PLoS Comput. Biol. 4, e1000028 (2008).

    ADS  MathSciNet  Google Scholar 

  16. Szigeti, B., Deogade, A. & Webb, B. Searching for motifs in the behaviour of larval Drosophila melanogaster and Caenorhabditis elegans reveals continuity between behavioural states. J. R. Soc. Interface 12, 20150899 (2015).

    Google Scholar 

  17. Steven W, F. et al. Serotonin and the neuropeptide PDF initiate and extend opposing behavioral states in C. elegans. Cell 154, 1023–1035 (2013).

    Google Scholar 

  18. Strogatz, S. H. Nonlinear Dynamics and Chaos with Student Solutions Manual: with Applications to Physics, Biology, Chemistry, and Engineering (CRC Press, 2018).

  19. Nolte, D. D. The tangled tale of phase space. Phys. Today 63, 33–38 (2010).

    Google Scholar 

  20. Durbin, J. & Koopman, S. J. Time Series Analysis by State Space Methods (Oxford Univ. Press, 2012).

  21. Palis, J. & de Melo, W. Geometric Theory of Dynamical Systems (Springer, 1982).

  22. Casdagli, M., Eubank, S., Farmer, J. D. & Gibson, J. State space reconstruction in the presence of noise. Physica D 51, 52–98 (1991).

    ADS  MathSciNet  MATH  Google Scholar 

  23. Broomhead, D. S. & King, G. P. Extracting qualitative dynamics from experimental data. Physica D 20, 217–236 (1986).

    ADS  MathSciNet  MATH  Google Scholar 

  24. Sugihara, G. & May, R. M. Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344, 734 (1990).

    ADS  Google Scholar 

  25. Tajima, S., Yanagawa, T., Fujii, N. & Toyoizumi, T. Untangling brain-wide dynamics in consciousness by cross-embedding. PLoS Comput. Biol. 11, e1004537 (2015).

    ADS  Google Scholar 

  26. Kantz, H. & Schreiber, T. Nonlinear Time Series Analysis Vol. 7 (Cambridge Univ. Press, 2004).

  27. Read, P. Phase portrait reconstruction using multivariate singular systems analysis. Physica D 69, 353–365 (1993).

    ADS  MATH  Google Scholar 

  28. Ye, H. & Sugihara, G. Information leverage in interconnected ecosystems: overcoming the curse of dimensionality. Science 353, 922–925 (2016).

    ADS  Google Scholar 

  29. Packard, N. H., Crutchfield, J. P., Farmer, J. D. & Shaw, R. S. Geometry from a time series. Phys. Rev. Lett. 45, 712 (1980).

    ADS  Google Scholar 

  30. Takens, F. Detecting strange attractors in turbulence. Dyn. Syst. Turbul. 898, 366–381 (1981).

    MathSciNet  MATH  Google Scholar 

  31. Hyvärinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 10, 626–634 (1999).

    Google Scholar 

  32. Gibson, J. F., Doyne Farmer, J., Casdagli, M. & Eubank, S. An analytic approach to practical state space reconstruction. Physica D 57, 1–30 (1992).

    ADS  MathSciNet  MATH  Google Scholar 

  33. Lorenz, E. Predictability: a problem partly solved. In Seminar on Predictability, 4–8 September 1995 Vol. 1, 1–18 (ECMWF, 1995); https://www.ecmwf.int/node/10829

  34. Aurell, E., Boffetta, G., Crisanti, A., Paladin, G. & Vulpiani, A. Predictability in the large: an extension of the concept of Lyapunov exponent. J. Phys. A 30, 1–26 (1997).

    ADS  MathSciNet  MATH  Google Scholar 

  35. Judd, K. & Mees, A. Embedding as a modeling problem. Physica D 120, 273–286 (1998).

    ADS  MATH  Google Scholar 

  36. Stephens, G. J., Bueno de Mesquita, M., Ryu, W. S. & Bialek, W. Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans. Proc. Natl Acad. Sci. USA 108, 7286–7289 (2011).

    ADS  Google Scholar 

  37. Broekmans, O. D., Rodgers, J. B., Ryu, W. S. & Stephens, G. J. Resolving coiled shapes reveals new reorientation behaviors in C. elegans. eLife 5, e17227 (2016).

    Google Scholar 

  38. Croll, N. A. Behavioural analysis of nematode movement. Adv. Parasitol. 13, 71–122 (1975).

    Google Scholar 

  39. Costa, A. C., Ahamed, T. & Stephens, G. J. Adaptive, locally linear models of complex dynamics. Proc. Natl Acad. Sci. USA 116, 1501–1510 (2019).

    MathSciNet  MATH  Google Scholar 

  40. Schwarz, R. F., Branicky, R., Grundy, L. J., Schafer, W. R. & Brown, A. E. X. Changes in postural syntax characterize sensory modulation and natural variation of C. elegans locomotion. PLoS Comput. Biol. 11, e1004322 (2015).

    ADS  Google Scholar 

  41. Gomez-Marin, A., Stephens, G. J. & Brown, A. E. X. Hierarchical compression of Caenorhabditis elegans locomotion reveals phenotypic differences in the organization of behaviour. J. R. Soc. Interface 13, 20160466 (2016).

  42. Donnelly, J. L. et al. Monoaminergic orchestration of motor programs in a complex C. elegans behavior. PLoS Biol. 11, e1001529 (2013).

    Google Scholar 

  43. Gray, J. M., Hill, J. J. & Bargmann, C. I. A circuit for navigation in Caenorhabditis elegans. Proc. Natl Acad. Sci. USA 102, 3184–3191 (2005).

    ADS  Google Scholar 

  44. Ben Arous, J., Laffont, S. & Chatenay, D. Molecular and sensory basis of a food related two-state behavior in C. elegans. PLoS ONE 4, e7584 (2009).

  45. Stern, S., Kirst, C. & Bargmann, C. I. Neuromodulatory control of long-term behavioral patterns and individuality across development. Cell 171, 1649–1662 (2017).

    Google Scholar 

  46. Banks, J., Brooks, J., Cairns, G., Davis, G. & Stacey, P. On Devaney’s definition of chaos. Am. Math. Mon. 99, 332–334 (1992).

    MathSciNet  MATH  Google Scholar 

  47. So, P., Francis, J. T., Netoff, T. I., Gluckman, B. J. & Schiff, S. J. Periodic orbits: a new language for neuronal dynamics. Biophys. J. 74, 2776–2785 (1998).

    ADS  Google Scholar 

  48. Mishra, N., Hasse, M., Biswal, B. & Singh, H. P. Reliability of unstable periodic orbit based control strategies in biological systems. Chaos 25, 043104 (2015).

    ADS  MathSciNet  Google Scholar 

  49. Pei, X. & Moss, F. Characterization of low-dimensional dynamics in the crayfish caudal photoreceptor. Nature 379, 618 (1996).

    ADS  Google Scholar 

  50. Schiff, S. J. et al. Controlling chaos in the brain. Nature 370, 615 (1994).

    ADS  Google Scholar 

  51. Lathrop, D. P. & Kostelich, E. J. Characterization of an experimental strange attractor by periodic orbits. Phys. Rev. A 40, 4028 (1989).

    ADS  MathSciNet  Google Scholar 

  52. Barrio, R., Dena, A. & Tucker, W. A database of rigorous and high-precision periodic orbits of the Lorenz model. Comput. Phys. Commun. 194, 76–83 (2015).

    ADS  MATH  Google Scholar 

  53. Cvitanović, P. Invariant measurement of strange sets in terms of cycles. Phys. Rev. Lett. 61, 2729 (1988).

    ADS  MathSciNet  Google Scholar 

  54. Pierce-Shimomura, J. T., Morse, T. M. & Lockery, S. R. The fundamental role of pirouettes in Caenorhabditis elegans chemotaxis. J. Neurosci. 19, 9557–9569 (1999).

    Google Scholar 

  55. Gjorgjieva, J., Biron, D. & Haspel, G. Neurobiology of Caenorhabditis elegans locomotion: where do we stand? Bioscience 64, 476–486 (2014).

    Google Scholar 

  56. Pikovsky, A. & Politi, A. Lyapunov Exponents: a Tool to Explore Complex Dynamics (Cambridge Univ. Press, 2016).

  57. Young, L.-S. Dimension, entropy and Lyapunov exponents. Ergod. Theory Dyn. Syst. 2, 109–124 (1982).

    MathSciNet  MATH  Google Scholar 

  58. Frederickson, P., Kaplan, J. L., Yorke, E. D. & Yorke, J. A. The Liapunov dimension of strange attractors. J. Differ. Equ. 49, 185–207 (1983).

    ADS  MathSciNet  MATH  Google Scholar 

  59. Sprott, J. C. Elegant Chaos (World Scientific, 2010).

  60. Dressler, U. Symmetry property of the Lyapunov spectra of a class of dissipative dynamical systems with viscous damping. Phys. Rev. A 38, 2103 (1988).

    ADS  Google Scholar 

  61. Dettmann, C. P. & Morriss, G. Proof of Lyapunov exponent pairing for systems at constant kinetic energy. Phys. Rev. E 53, R5545 (1996).

    ADS  Google Scholar 

  62. Loveless, J., Lagogiannis, K. & Webb, B. Modelling the mechanics of exploration in larval Drosophila. PLoS Comput. Biol. 15, e1006635 (2019).

    ADS  Google Scholar 

  63. Kato, S. et al. Global brain dynamics embed the motor command sequence of Caenorhabditis elegans. Cell 163, 656–669 (2015).

    Google Scholar 

  64. Chen, X., Randi, F., Leifer, A. M. & Bialek, W. Searching for collective behavior in a small brain. Phys. Rev. E 99, 052418 (2019).

    ADS  Google Scholar 

  65. Cook, S. J. et al. Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71 (2019).

    ADS  Google Scholar 

  66. Gao, S. et al. Excitatory motor neurons are local oscillators for backward locomotion. eLife 7, e29915 (2018).

  67. Xu, T. et al. Descending pathway facilitates undulatory wave propagation in Caenorhabditis elegans through gap junctions. Proc. Natl Acad. Sci. USA 115, E4493–E4502 (2018).

    Google Scholar 

  68. Revzen, S. & Guckenheimer, J. M. Finding the dimension of slow dynamics in a rhythmic system. J. R. Soc. Interface 9, 957–971 (2011).

    Google Scholar 

  69. Jackson, E. A. The OPCL control method for entrainment, model-resonance, and migration actions on multiple-attractor systems. Chaos 7, 550–559 (1997).

    ADS  MathSciNet  MATH  Google Scholar 

  70. Fang-Yen, C. et al. Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc. Natl Acad. Sci. USA 107, 20323–20328 (2010).

    ADS  Google Scholar 

  71. Backholm, M., Kasper, A., Schulman, R., Ryu, W. & Dalnoki-Veress, K. The effects of viscosity on the undulatory swimming dynamics of C. elegans. Phys. Fluids 27, 091901 (2015).

    ADS  Google Scholar 

  72. Butler, V. J. et al. A consistent muscle activation strategy underlies crawling and swimming in Caenorhabditis elegans. J. R. Soc. Interface 12, 20140963 (2015).

    Google Scholar 

  73. Boyle, J. H., Berri, S. & Cohen, N. Gait modulation in C. elegans: an integrated neuromechanical model. Front. Comput. Neurosci. 6, 10 (2012).

    Google Scholar 

  74. Wen, Q. et al. Proprioceptive coupling within motor neurons drives C. elegans forward locomotion. Neuron 76, 750–761 (2012).

    Google Scholar 

  75. Daems, D. & Nicolis, G. Entropy production and phase space volume contraction. Phys. Rev. E 59, 4000 (1999).

    ADS  MathSciNet  Google Scholar 

  76. Bollt, E. M. & Santitissadeekorn, N. Applied and Computational Measurable Dynamics Vol. 18 (SIAM, 2013).

  77. Brennan, C. & Proekt, A. A quantitative model of conserved macroscopic dynamics predicts future motor commands. eLife 8, e46814 (2019).

  78. Pérez-Hernández, G., Paul, F., Giorgino, T., De Fabritiis, G. & Noé, F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 139, 015102 (2013).

  79. Brunton, S. L. & Kutz, J. N. Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control (Cambridge Univ. Press, 2019).

  80. Farmer, J. D. & Sidorowich, J. J. Predicting chaotic time series. Phys. Rev. Lett. 59, 845 (1987).

    ADS  MathSciNet  Google Scholar 

  81. Xing, E. P., Jordan, M. I., Russell, S. J. & Ng, A. Y. Distance metric learning with application to clustering with side-information. In Advances in Neural Information Processing Systems 15 521–528 (MIT Press, 2003).

  82. Pathak, J., Lu, Z., Hunt, B. R., Girvan, M. & Ott, E. Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos 27, 121102 (2017).

    ADS  MathSciNet  MATH  Google Scholar 

  83. MATLAB v.9.3.0 (R2017b) (MathWorks, 2017).

  84. Javer, A. et al. An open-source platform for analyzing and sharing worm-behavior data. Nat. Methods 15, 645–646 (2018).

    Google Scholar 

  85. Sulston, J. E. & Brenner, S. The DNA of C. elegans. Genetics 77, 95–104 (1974).

    Google Scholar 

  86. Brenner, S. The genetics of Caenorhabditis elegans. Genetics 77, 71–94 (1974).

    Google Scholar 

  87. Yemini, E., Kerr, R. A. & Schafer, W. R. Preparation of samples for single-worm tracking. Cold Spring Harb. Protoc. 2011, 1475–1479 (2011).

    Google Scholar 

  88. Casdagli, M., Sauer, T. & Yorke, J. A. Embedology. J. Stat. Phys. 65, 579–616 (1991).

    ADS  MathSciNet  MATH  Google Scholar 

  89. Stark, J., Broomhead, D. S., Davies, M. & Huke, J. Delay embeddings for forced systems. II. Stochastic forcing. J. Nonlinear Sci. 13, 519–577 (2003).

    ADS  MathSciNet  Google Scholar 

  90. Muldoon, M. R., Broomhead, D. S., Huke, J. P. & Hegger, R. Delay embedding in the presence of dynamical noise. Dyn. Stab. Syst. 13, 175–186 (1998).

  91. Stark, J. Delay embeddings for forced systems. I. Deterministic forcing. J. Nonlinear Sci. 9, 255–332 (1999).

    ADS  MathSciNet  MATH  Google Scholar 

  92. Huke, J. P. & Broomhead, D. S. Embedding theorems for non-uniformly sampled dynamical systems. Nonlinearity 20, 2205 (2007).

    MathSciNet  MATH  Google Scholar 

  93. Deyle, E. R. & Sugihara, G. Generalized theorems for nonlinear state space reconstruction. PLoS ONE 6, e18295 (2011).

    ADS  Google Scholar 

  94. Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–148 (1963).

    ADS  MathSciNet  MATH  Google Scholar 

  95. Vautard, R. & Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Physica D 35, 395–424 (1989).

    ADS  MathSciNet  MATH  Google Scholar 

  96. Farmer, J. D. Information dimension and the probabilistic structure of chaos. Z. Naturforsch. A 37, 1304–1326 (1982).

    ADS  MathSciNet  Google Scholar 

  97. Kennel, M. B., Brown, R. & Abarbanel, H. D. I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411 (1992).

    ADS  Google Scholar 

  98. Hammel, S. M., Yorke, J. A. & Grebogi, C. Do numerical orbits of chaotic dynamical processes represent true orbits? J. Complex. 3, 136–145 (1987).

    MathSciNet  MATH  Google Scholar 

  99. Nusse, H. E. & Yorke, J. A. Is every approximate trajectory of some process near an exact trajectory of a nearby process? Commun. Math. Phys. 114, 363–379 (1988).

    ADS  MathSciNet  MATH  Google Scholar 

  100. Pawelzik, K. & Schuster, H. Unstable periodic orbits and prediction. Phys. Rev. A 43, 1808 (1991).

    ADS  Google Scholar 

  101. Badii, R. et al. Progress in the analysis of experimental chaos through periodic orbits. Rev. Mod. Phys. 66, 1389 (1994).

    ADS  MathSciNet  Google Scholar 

  102. Kantz, H. A robust method to estimate the maximal Lyapunov exponent of a time series. Phys. Lett. A 185, 77–87 (1994).

    ADS  Google Scholar 

  103. Deyle, E. R., May, R. M., Munch, S. B. & Sugihara, G. Tracking and forecasting ecosystem interactions in real time. Proc. R. Soc. B 283, 20152258 (2016).

    Google Scholar 

  104. Abarbanel, H. D. I., Brown, R. & Kennel, M. B. Variation of Lyapunov exponents on a strange attractor. J. Nonlinear Sci. 1, 175–199 (1991).

    ADS  MathSciNet  MATH  Google Scholar 

  105. Abarbanel, H. D. I., Brown, R. & Kennel, M. B. Local Lyapunov exponents computed from observed data. J. Nonlinear Sci. 2, 343–365 (1992).

    ADS  MathSciNet  MATH  Google Scholar 

  106. Guckenheimer, J. & Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Springer, 1983).

Download references

Acknowledgements

We thank D. Jordan, I. Etheredge and A. Celani for comments. L. Hebert (OIST Graduate University) developed the custom machine-learning solution for pose estimation of worms in on-food conditions. We would also like to express our gratitude to I. Maruyama for his support during the project. This work was supported by OIST Graduate University (T.A., G.J.S.), a programme grant from the Netherlands Organization for Scientific Research (A.C.C., G.J.S.), Vrije Universiteit Amsterdam (G.J.S.) and the Japan Society for the Promotion of Science (T.A.).

Author information

Authors and Affiliations

  1. Biological Physics Theory Unit, OIST Graduate University, Okinawa, Japan

    Tosif Ahamed & Greg J. Stephens

  2. Department of Physics and Astronomy, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands

    Antonio C. Costa & Greg J. Stephens

Authors
  1. Tosif Ahamed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antonio C. Costa
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Greg J. Stephens
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

T.A., A.C.C. and G.J.S. designed the research, performed the research, analysed the data and wrote the paper.

Corresponding author

Correspondence to Greg J. Stephens.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 The predictability Tpred as a function of K and m for N = 12 individual worms.

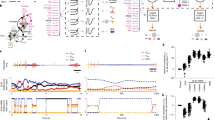
a, Tpred as a functon of K. b, Tpred as a function of m. We find similar curves across worms, despite the differences in their detailed dynamics. Note that while the distance metric in the SVD space (b) and the space of delays (a) is different, which could result in inconsistencies in the estimation of Tpred, we find only minor differences between the maximum Tpred in the two cases (gray bar in B). Inset shows the normalized singular value spectrum, which does not have a clear cutoff for any worm. c, Expanded inset in B showing the normalized singular value spectrum. d, State space captures a commonly observed sequence where long reversals transition to forward via a deep body bends seen here as a large excitation in Xt2 as the reversal ends. Here we see that the blue (backward) and red (forward) bundles are smoothly connected via a large transient along the turning mode \({X}_{{t}_{2}}\) (data from the example worm in Fig. 3b–e).

Extended Data Fig. 2 Dominant state space modes are stable across different embedding dimensions, with distinct groups independently capturing forward, reversal and turning behaviors.

a–c, Behavioral modes estimated for the worm in Fig. 3 for dimensions, m = 6 (a), m = 7 (b), and m = 8 (c); embedding window is set to K = 12 frames. The modes retain their interpretability across dimensions. In a 6-dimensional embedding, there are two forward, two backward and two turning modes. In 7 dimensions one of the turning modes further splits into an omega-turn like mode (\({\Gamma }_{{t}_{3}}\)) and a delta-turn like mode (\({\Gamma }_{{t}_{1}}\)), while \({\Gamma }_{{t}_{2}}\) changes little. Furthermore, the reversal modes are more separable in 7 dimensions. The 8-dimensional state space retains the forward, reversal and turning dynamics along with an additional and subtle head-bending.

Extended Data Fig. 3 The ensemble embedding across all N = 12 worms is constructed from their concatenated posture time series and characterized by \(K^*=10\) and \(m^*=7\).

a–b, Tpred as a function of K and m. We set \(K^*=10\), approximately when Tpred begins to decrease, and show Tpred(m) at this \(K^*\). We show the resulting modes for m = 6 and the gray bar denotes \(T_{pred}(K = K^*)\). c, m = 7 (d), and m = 8 (e), and these are qualitatively similar to those obtained from our representative worm of Extended Data Fig. 2. The additional modes present for embeddings greater than \(m^*=7\) offer only minor improvements in predictability.

Extended Data Fig. 4 Ensemble embedding for different values of K and m.

a–c, Behavioral modes estimated from the ensemble for K = 5, and dimensions, m = 6 (a), m = 7 (b), and m = 8 (c). d–f, Same as above but for K = 15. The modes are qualitatively similar across this variation.

Extended Data Fig. 5 The dominant off-food modes are similar to those of on-food roaming behavior and on-food behavior of npr-1 mutant worms.

We analyze a collection of N = 25 on-food ‘roaming’ N2 worms, N = 25 on-food ‘dwelling’ N2 worms, and N = 7 on-food mutant npr-1 worms from an open access dataset84 (Methods, see also Extended Data Fig. 10a). We show Tpred(m) for (a) on-food N2 roaming worms and (b) on-food npr-1 mutants. c–d, Kymographs of the \(m^*=7\) primary modes from roaming and npr-1 worms coincide, both with each other and with the off-food N2 modes in Fig. 3. The similarity of these embeddings provide new, posture-scale evidence that the NPR-1 mutation overrides the switch to dwelling45. e–f, The combined embedding of roaming-dwelling on-food behavior exhibits an additional ~ 6 modes with small but notable additional Tpred, which was also observed in off-food behavior in the ensemble embedding, Extended Data Fig. 3, and for some individual worms, Extended Data Fig. 1b.

Extended Data Fig. 6 Maximum Lyapunov exponent for different worms and the full Lyapunov spectrum in different embedding dimensions.

a, To quantify the state space divergence we plot the logarithm of the average distance between a trajectory and its nearest neighbors, averaged over several starting reference trajectories. For each worm we find that, after a transient, there is linear region showing exponential divergence. The slope of the linear region provides an estimate of the maximal Lyapunov exponent λmax and the positive exponents are an indication of chaos in worm behavior. b–d, Lyapunov spectra computed from reconstructions of worm behavior in different embedding dimensions. Conjugate pairing of Lyapunov exponents is robustly observed in dimensions 6 and above.

Extended Data Fig. 7 Detecting periodic orbits in the Lorenz System.

a–e, We compare UPO trajectories for the Lorenz system computed from high precision numerical estimates52 (red) with periodic orbits detected using our recurrence based approach (grey) (only 3 UPOs are shown for period 5). The closely-matching trajectories also exhibit agreement between the Floquet exponents estimated from analytical Jacobians (red text) and Local Lyapunov exponents obtained from the estimated Jacobians (grey text). Note that in (e), a fixed point (period-0 orbit) can only be detected by neighboring spiraling trajectories, leading to an overestimation of the exponent. f, Boxplot comparing the entire distribution of Floquet exponents for UPOs up to period 10 (red bars denote the median).

Extended Data Fig. 8 Recurrence Function and Period-1 UPOs.

a, The recurrence function ϵ(r, t) from the same worm in Fig. 3 for 120 frames and 5000 closest recurrences (top). Local minima of this function at times t*, as seen in the average 〈ϵ(r, t)〉r shown below correspond to close recurrences and identify periodic orbits of length t*. The first local minimum is the smallest period pmin, which is 37 frames in this example. For a given value of r, ϵ(r, t*) gives the distance threshold at which we must look to find a periodic orbit of length t*. b, Probability distribution of phase velocities \(\dot{\phi }\) and third eigenworm coefficient a3, which is proportional to mean body curvature, across all period-1 orbits of duration pmin from all worms in the dataset. We see two clusters corresponding to forward and backward locomotion, as well as orbits with a dorsal or ventral bias (for example orbits at bottom right and top left). c, Example period-1 orbits from the same worm in (a) corresponding to forward (top) and backward (bottom) locomotion.

Extended Data Fig. 9 Example E(τ) curves.

a, Error curves are plotted for different embedding dimensions for the Lorenz system state space reconstruction \((K^* = 25)\). b, Error curves in different embedding dimensions for the sample worm in Fig. 3b–e. Better embeddings lead to a lower error curve. The ratio of the area between these curves and the saturation value es to es estimates Tpred. c, A schematic showing the fixed point algorithm for robust estimation of the asymptote es, and the area Δ.

Extended Data Fig. 10 Roaming/dwelling states and further embedding details.

a, Centroid speed and angular speed (averaged in 10 s windows) for the collection of worms used in the N2 on food dataset (red and blue) and the npr-1 dataset (black).We initially collected 150 recordings of N2 worms crawling on food-full plates from an open dataset84. From these, we selected 25 worms with a large fraction of dwelling states (blue) and 25 worms with a large fraction of roaming states (red), defined as in17. We downsample the data to 3 Hz (consistent with17), and average the centroid speed and angular speed in 10 s windows. Roaming and dwelling states are identified by a threshold defined by the line y = x/450 in the plane defined by x, the angular speed, and y, the centroid speed. Points above the line (high speed and low angular speed) are classified as roaming, while points below the line (low speed and high angular speed) are classified as dwelling. Data from npr-1 mutants (black) show predominantly roaming behavior, consistent with previous reports45. b, Example of the one step error, E(1, Nb) curve used to pick the number of nearest neighbors. This was calculated on the same worm as in Fig. 3b–e. c, A transient can be seen For the Lorenz system before the linear regime indicating exponential growth of local finite-sized perturbations (sized ≈ 10−4) begins. d, Transient decreases when perturbations of size ≈ 10−8 are used.

Supplementary information

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ahamed, T., Costa, A.C. & Stephens, G.J. Capturing the continuous complexity of behaviour in Caenorhabditis elegans. Nat. Phys. 17, 275–283 (2021). https://doi.org/10.1038/s41567-020-01036-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-020-01036-8

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing