Abstract
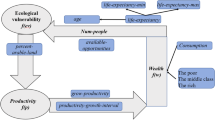
The world’s rural poor rely heavily on their immediate natural environment for subsistence and suffer high rates of morbidity and mortality from infectious diseases. We present a general framework for modelling subsistence and health of the rural poor by coupling simple dynamic models of population ecology with those for economic growth. The models show that feedbacks between the biological and economic systems can lead to a state of persistent poverty. Analyses of a wide range of specific systems under alternative assumptions show the existence of three possible regimes corresponding to a globally stable development equilibrium, a globally stable poverty equilibrium and bistability. Bistability consistently emerges as a property of generalized disease–economic systems for about a fifth of the feasible parameter space. The overall proportion of parameters leading to poverty is larger than that resulting in healthy/wealthy development. All the systems are found to be most sensitive to human disease parameters. The framework highlights feedbacks, processes and parameters that are important to measure in studies of rural poverty to identify effective pathways towards sustainable development.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
UN General Assembly United Nations Millenium Declaration (UN, 2000).
World Bank World Bank Annual Report 2014 (MIT Press, 2014).
Rural Poverty Report (IFAD, 2000).
Lozano, R. et al. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: a systematic analysis for the global burden of disease study 2010. Lancet 380, 2095–2128 (2013).
Whitmee, S. et al. Safeguarding human health in the Anthropocene epoch: report of The Rockefeller Foundation–Lancet Commission on planetary health. Lancet 386, 1973–2028 (2015).
Assessment, M. E. Ecosystems and Human Well-Being: Wetlands and Water (World Resources Institute, 2005).
Dasgupta, P. Human Well-Being and the Natural Environment (Oxford Univ. Press, 2001).
Bonds, M. H., Dobson, A. P. & Keenan, D. C. Disease ecology, biodiversity, and the latitudinal gradient in income. PLoS Biol. 10, e1001456 (2012).
Sachs, J. et al. Ending Africa’s poverty trap. Brookings Pap. Eco. Ac. 2004, 117–240 (2004).
Bonds, M., Keenan, D., Rohani, P. & Sachs, J. Poverty trap formed by the ecology of infectious diseases. Proc. R. Soc. B 277, 1185–1192 (2010).
Ngonghala, C. N. et al. Poverty, disease, and the ecology of complex systems. PLoS Biol. 12, e1001827 (2014).
Solow, R. A contribution to the theory of economic growth. Q. J. Econ. 70, 65–94 (1956).
Azariadis, C. & Stachurski, J. in Handbook of Economic Growth Vol. 1A (eds Aghion, P. & Durlauf, S.) 295–384 (North Holland, 2005).
Schaible, U. E. & Stefan, H. Malnutrition and infection: complex mechanisms and global impacts. PLoS Med. 4, e115 (2007).
Dasgupta, P. Nutritional status, the capacity for work, and poverty traps. J. Econometrics 77, 5–37 (1997).
Alsan, M. M., Westerhaus, M., Herce, M., Nakashima, K. & Farmer, P. E. Poverty, global health, and infectious disease: lessons from Haiti and Rwanda. Infect. Dis. Clin. N. Am. 25, 611–622 (2011).
Barro, R. & Sala-i Martin, X. Economic Growth (MIT Press, 1999).
Gurney, W. & Nisbet, R. M. Ecological Dynamics (Oxford Univ. Press, 1998).
Becker, G. S. Health as human capital: synthesis and extensions. Oxford Econ. Pap. 59, 379–410 (2007).
Gyimah-Brempong, K. & Wilson, M. Health human capital and economic growth in sub- Saharan African and OECD countries. Q. Rev. Econ. Finance 44, 296–320 (2004).
Raffel, T. R., Martin, L. B. & Rohr, J. R. Parasites as predators: unifying natural enemy ecology. Trends Ecol. Evol. 23, 610–618 (2008).
Lafferty, K. D. et al. A general consumer–resource population model. Science 349, 854–857 (2015).
Anderson, R. & May, R. Infectious Diseases of Humans: Dynamics and Control (Oxford Univ. Press, 1992).
Smith, H. L. Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems (Mathematical Surveys and Monographs Vol. 41, American Mathematical Society, 2008).
Marino, S., Hogue, I., Ray, C. & Kirschner, D. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 254, 178–196 (2008).
Barrett, C. B., Travis, A. J. & Dasgupta, P. On biodiversity conservation and poverty traps. Proc. Natl Acad. Sci. USA 108, 13907–13912 (2011).
Sachs, J. End of Poverty: Economic Possibilities of Our Time (Penguin, 2005).
Bloom, D. E., Canning, D. & Sevilla, J. The effect of health on economic growth: a production function approach. World Dev. 32, 1–13 (2004).
Farmer, P. E. et al. Reduced premature mortality in Rwanda: lessons from success. BMJ 346, f65 (2013).
Binagwaho, A. et al. Rwanda 20 years on: investing in life. Lancet 384, 371–375 (2014).
Plucinski, M., Ngonghala, C. & Bonds, M. H. Health safety nets can break cycles of poverty and disease: a stochastic ecological model. J. R. Soc. Interface 8, 1796–1803 (2011).
Noy-Meir, I. Stability of grazing systems: an application of predator–prey graphs. J. Ecol. 63, 459–481 (1975).
Rietkerk, M. & Van de Koppel, J. Alternate stable states and threshold effects in semi-arid grazing systems. Oikos 79, 69–76 (1997).
van de Koppel, J., Rietkerk, M. & Weissing, F. J. Catastrophic vegetation shifts and soil degradation in terrestrial grazing systems. Trends Ecol. Evol. 12, 352–356 (1997).
Hillier, J. G. & Birch, A. N. E. A bi-trophic mathematical model for pest adaptation to a resistant crop. J. Theor. Biol. 215, 305–319 (2002).
Bailey, T. J. N. The Mathematical Theory of Infectious Diseases and its Application 2nd edn (Griffin, 1975).
Hethcote, H. Qualitative analyses of communicable disease models. Math. Biosci. 28, 335–356 (1976).
Keeling, M. J. & Rohani, P. Modelling Infectious Diseases (Princeton Univ. Press, 2007).
Acknowledgements
This work benefited from the working group ‘Land use change and infectious diseases’ conducted both at the National Socio-Environmental Synthesis Center (funded from NSF DBI-1052875) and the National Center for Ecological Analysis and Synthesis (funded by the University of California, Santa Barbara and the state of California). We are grateful to both centres for providing excellent interactive venues to discuss some of the analysis and results of the models, and to other members of the working group for their valuable feedback. A.P.D. and M.M.P. acknowledge SFI. M.H.B. and C.N.N. are supported by NIH grant 5K01TW008773-06 from Fogarty International Center and a Scholar Award in Complex Systems Science from the James S. McDonnell Foundation to M.H.B. G.A.D.L. was supported by the National Science Foundation (CNH grant no. 1414102), NIH grants (R01GM109499, R01TW010286), the Bill and Melinda Gates Foundation, Stanford GDP SEED (grant no. 1183573-100-GDPAO) and the SNAP-NCEAS-supported working group ‘Ecological levers for health: advancing a priority agenda for disease ecology and planetary health in the 21st century’. We thank S. and V. Della Pietras for helpful comments on the manuscript.
Author information
Authors and Affiliations
Contributions
C.N.N. and M.H.B. conceived the paper, C.N.N. conducted analysis. All authors performed research and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Supplementary Information
Details of the models used in the analysis
Rights and permissions
About this article
Cite this article
Ngonghala, C.N., De Leo, G.A., Pascual, M.M. et al. General ecological models for human subsistence, health and poverty. Nat Ecol Evol 1, 1153–1159 (2017). https://doi.org/10.1038/s41559-017-0221-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41559-017-0221-8
This article is cited by
-
Farm-level pathways to food security: beyond missing markets and irrational peasants
Agriculture and Human Values (2022)
-
Land use impacts on parasitic infection: a cross-sectional epidemiological study on the role of irrigated agriculture in schistosome infection in a dammed landscape
Infectious Diseases of Poverty (2021)
-
Towards an ecosystem model of infectious disease
Nature Ecology & Evolution (2021)
-
Emerging human infectious diseases and the links to global food production
Nature Sustainability (2019)
-
The ecology of rural poverty
Nature Ecology & Evolution (2017)