Abstract
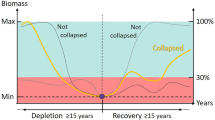
Predicting population declines is a key challenge in the face of global environmental change. Abundance-based early warning signals have been shown to precede population collapses; however, such signals are sensitive to the low reliability of abundance estimates. Here, using historical data on whales harvested during the 20th century, we demonstrate that early warning signals can be present not only in the abundance data, but also in the more reliable body size data of wild populations. We show that during the period of commercial whaling, the mean body size of caught whales declined dramatically (by up to 4 m over a 70-year period), leading to early warning signals being detectable up to 40 years before the global collapse of whale stocks. Combining abundance and body size data can reduce the length of the time series required to predict collapse, and decrease the chances of false positive early warning signals.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Scheffer, M. et al. Anticipating critical transitions. Science 338, 344–348 (2012).
Carpenter, S. R. et al. Early warnings of regime shifts: a whole-ecosystem experiment. Science 332, 1079–1082 (2011).
Drake, J. & Griffen, B. Early warning signals of extinction in deteriorating environments. Nature 467, 456–459 (2010).
Kéfi, S., Dakos, V., Scheffer, M., Van Nes, E. H. & Rietkerk, M. Early warning signals also precede non-catastrophic transitions. Oikos 122, 641–648 (2013).
Dakos, V. et al. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 7, e41010 (2012).
Clements, C. F., Drake, J. M., Griffiths, J. I. & Ozgul, A. Factors influencing the detectability of early warning signals of population collapse. Am. Nat. 186, 50–58 (2015).
Burthe, S. J. et al. Do early warning indicators consistently predict nonlinear change in long-term ecological data? J. Appl. Ecol. 53, 666–676 (2015).
Pauly, D., Hilborn, R. & Branch, T. A. Fisheries: does catch reflect abundance? Nature 494, 303–306 (2013).
Clements, C. F. & Ozgul, A. Including trait-based early warning signals helps predict population collapse. Nat. Commun. 7, 10984 (2016).
Ozgul, A., Bateman, A. W., English, S., Coulson, T. & Clutton-Brock, T. H. Linking body mass and group dynamics in an obligate cooperative breeder. J. Anim. Ecol. 83, 1357–1366 (2014).
Ling, S. D., Johnson, C. R., Frusher, S. D. & Ridgway, K. R. Overfishing reduces resilience of kelp beds to climate-driven catastrophic phase shift. Proc. Natl Acad. Sci. USA 106, 22341–22345 (2009).
Anderson, C. N. K. et al. Why fishing magnifies fluctuations in fish abundance. Nature 452, 835–839 (2008).
Uusi-Heikkilä, S. et al. Altered trait variability in response to size-selective mortality. Biol. Lett. 12(9), 20160584 (2016).
Hilborn, R. et al. State of the world’s fisheries. Annu. Rev. Envir. Resour. 28, 359–399 (2003).
Baker, C. S. & Clapham, P. J. Modelling the past and future of whales and whaling. Trends Ecol. Evol. 19, 365–371 (2004).
Jackson, J. B. et al. Historical overfishing and the recent collapse of coastal ecosystems. Science 293, 629–637 (2001).
Gerlach, S. Marine Pollution (Springer, 1981).
Dierauf, L. & Gulland, F. M. D. CRC Handbook of Marine Mammal Medicine: Health, Disease, and Rehabilitation 2nd edn (CRC, 2001).
Springer, A. et al. Sequential megafaunal collapse in the North Pacific Ocean: an ongoing legacy of industrial whaling? Proc. Natl Acad. Sci. USA 100, 12223–12228 (2003).
Roman, J. & Palumbi, S. R. Whales before whaling in the North Atlantic. Science 301, 508–510 (2003).
Basberg, B. L. Technological change in the Norwegian whaling industry. Res. Policy 11, 163–171 (1982).
Audzijonyte, A. et al. Trends and management implications of human-influenced life-history changes in marine ectotherms. Fish Fish. 17, 1005–1028 (2016).
Bannister, J. Great Whales (CSIRO, 2008).
Biggs, R., Carpenter, S. R. & Brock, W. A. Turning back from the brink: detecting an impending regime shift in time to avert it. Proc. Natl Acad. Sci. USA 106, 826–831 (2009).
Whitehead, H. Sperm Whales: Social Evolution in the Ocean (Univ. Chicago Press, 2003).
Rocha, J., Yletyinen, J., Biggs, R., Blenckner, T. & Peterson, G. Marine regime shifts: drivers and impacts on ecosystems services. Phil. Trans. R. Soc. B 370, 20130273 (2014).
Clarke, S. C. et al. Global estimates of shark catches using trade records from commercial markets. Ecol. Lett. 9, 1115–1126 (2006).
International Convention for the Regulation of Whaling, 1946 (IWC, 2014).
Rochet, M. J. et al. Do changes in environmental and fishing pressures impact marine communities? An empirical assessment. J. Appl. Ecol. 47, 741–750 (2010).
Wood, S. N. mgcv: Mixed GAM Computation Vehicle with GCV/AIC/REML Smoothness Estimation. R package version 1.8-6 (R Foundation for Statistical Computing, 2013).
R Development Core Team R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, 2016).
Taylor, B. L ., Chivers, S. J ., Larese, J. & Perrin, W. F. Generation Length and Percent Mature Estimates for IUCN Assessments of Cetaceans Administrative Report LJ-07-01 (National Marine Fisheries Service, 2007).
Pfister, C. A. & Stevens, F. R. The genesis of size variability in plants and animals. Ecology 83, 59–72 (2002).
Acknowledgements
This work was made possible by an ERC starting grant (no. 337785) to A.O. and an SNF international short visit grant (no. IZK0Z3_166526) to C.F.C. Whale illustrations by K. Askaroff.
Author information
Authors and Affiliations
Contributions
This work was jointly conceived by all the authors. C.F.C. performed the analyses and wrote the first draft of the manuscript. All co-authors contributed substantially to revisions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Notes 1,2; Supplementary Figures 1–8; Supplementary Table 1; Supplementary References. (PDF 494 kb)
Rights and permissions
About this article
Cite this article
Clements, C., Blanchard, J., Nash, K. et al. Body size shifts and early warning signals precede the historic collapse of whale stocks. Nat Ecol Evol 1, 0188 (2017). https://doi.org/10.1038/s41559-017-0188
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41559-017-0188
This article is cited by
-
Distribution shifts in Indo-Pacific humpback dolphins and the co-occurrence of marine heatwaves
Reviews in Fish Biology and Fisheries (2024)
-
A predictive timeline of wildlife population collapse
Nature Ecology & Evolution (2023)
-
Early warning signals have limited applicability to empirical lake data
Nature Communications (2023)
-
Detecting climate signals cascading through levels of biological organization
Nature Climate Change (2023)
-
The Neglected Role of Intraspecific Variation in Plastic Pollution Research
Anthropocene Science (2023)