Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Large molecular gas reservoirs in ancestors of Milky Way-mass galaxies nine billion years ago

Nature Astronomy volume 1, Article number: 0003 (2017) Cite this article

Subjects

Abstract

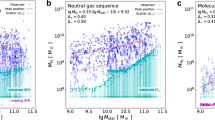
The gas accretion and star formation histories of galaxies like the Milky Way remain an outstanding problem in astrophysics1,2. Observations show that 8 billion years ago, the progenitors to Milky Way-mass galaxies were forming stars 30 times faster than today and were predicted to be rich in molecular gas3, in contrast to the low present-day gas fractions (<10%)4–6. Here we show the detection of molecular gas from the CO (J = 3–2) emission (rest-frame 345.8 GHz) in galaxies at redshifts z = 1.2–1.3, selected to have the stellar mass and star formation rate of the progenitors of today’s Milky Way-mass galaxies. The CO emission reveals large molecular gas masses, comparable to or exceeding the galaxy stellar masses, and implying that most of the baryons are in cold gas, not stars. The total luminosities of the galaxies from star formation and CO luminosities yield long gas consumption timescales. Compared to local spiral galaxies, the star formation efficiency, estimated from the ratio of total infrared luminosity (LIR) to CO emission, has remained nearly constant since redshift z = 1.2, despite the order of magnitude decrease in gas fraction, consistent with the results for other galaxies at this epoch7–10. Therefore, the physical processes that determine the rate at which gas cools to form stars in distant galaxies appear to be similar to that in local galaxies.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Images of Milky Way progenitors at redshifts z = 1.2–1.3.
Figure 2: SFE as a function of L'co.
Figure 3: The relationship between the molecular gas fraction and total stellar mass in galaxies at z = 1−1.5 compared with local galaxies.

Similar content being viewed by others

References

  1. Guedes, J., Callegari, S., Madau, P. & Mayer, L. Forming realistic late-type spirals in a ΛCDM universe: the Eris simulation. Astrophys. J. 742, 76 (2011).

    Article  ADS  Google Scholar 

  2. Martig, M., Bournaud, F., Croton, D. J., Dekel, A. & Teyssier, R. A diversity of progenitors and histories for isolated spiral galaxies. Astrophys. J. 756, 26 (2012).

    Article  ADS  Google Scholar 

  3. Papovich, C. et al. ZFOURGE/CANDELS: on the evolution of M* galaxy progenitors from z =3 to 0.5. Astrophys. J. 803, 26 (2015).

    Article  ADS  Google Scholar 

  4. Sage, L. J. Molecular gas in nearby galaxies. I: CO observations of a distance-limited sample. Astron. Astrophys. 272, 123–136 (1993).

    ADS  Google Scholar 

  5. Leroy, A. K. et al. Heracles: The HERA CO line extragalactic survey. Astron. J. 137, 4670–4696 (2009).

    Article  ADS  Google Scholar 

  6. Saintonge, A. et al. COLD GASS, an IRAM legacy survey of molecular gas in massive galaxies. I: relations between H2, H i, stellar content and structural properties. Mon. Not. R. Astron. Soc. 415, 32–60 (2011).

    Article  ADS  Google Scholar 

  7. Daddi, E. et al. Very high gas fractions and extended gas reservoirs in z = 1.5 disk galaxies. Astrophys. J. 713, 686–707 (2010).

    Article  ADS  Google Scholar 

  8. Magdis, G. E. et al. The molecular gas content of z = 3 Lyman break galaxies: evidence of a non-evolving gas fraction in main-sequence galaxies at z &gt; 2. Astrophys. J. 758, L9 (2012).

    Article  ADS  Google Scholar 

  9. Magnelli, B. et al. Dust temperature and CO–H2 conversion factor variations in the SFR-M plane. Astron. Astrophys. 548, A22 (2012).

    Article  Google Scholar 

  10. Tacconi, L. J. et al. Phibss: molecular gas content and scaling relations in z∼1-3 massive, main-sequence star-forming galaxies. Astrophys. J. 768, 74 (2013).

    Article  ADS  Google Scholar 

  11. Snaith, O. N. et al. The dominant epoch of star formation in the Milky Way formed the thick disk. Astrophys. J. 781, L31 (2014).

    Article  ADS  Google Scholar 

  12. Bernard, E. J. et al. The spatially-resolved star formation history of the M31 outer disc. Mon. Not. R. Astron. Soc. 453, L113–L117 (2015).

    Article  ADS  Google Scholar 

  13. Licquia, T. C. & Newman, J. A. Improved estimates of the Milky Way’s stellar mass and star formation rate from hierarchical Bayesian meta-analysis. Astrophys. J. 806, 96 (2015).

    Article  ADS  Google Scholar 

  14. De Lucia, G. et al. Elemental abundances in Milky Way-like galaxies from a hierarchical galaxy formation model. Mon. Not. R. Astron. Soc. 445, 970–987 (2014).

    Article  ADS  Google Scholar 

  15. Dekel, A. et al. Cold streams in early massive hot haloes as the main mode of galaxy formation. Nature 457, 451–454 (2009).

    Article  ADS  Google Scholar 

  16. Genzel, R. et al. The rapid formation of a large rotating disk galaxy three billion years after the Big Bang. Nature 442, 786–789 (2006).

    Article  ADS  Google Scholar 

  17. Tacconi, L. J. et al. High molecular gas fractions in normal massive star-forming galaxies in the young Universe. Nature 463, 781–784 (2010).

    Article  ADS  Google Scholar 

  18. Genzel, R. et al. Combined CO and dust scaling relations of depletion time and molecular gas fractions with cosmic time, specific star-formation rate, and stellar mass. Astrophys. J. 800, 20 (2015).

    Article  ADS  Google Scholar 

  19. Wisnioski, E. et al. The KMOS3D survey: design, first results, and the evolution of galaxy kinematics from 0.7 &lt;= z &lt;= 2.7. Astrophys. J. 799, 209 (2015).

    Article  ADS  Google Scholar 

  20. Ceverino, D., Dekel, A. & Bournaud, F. High-redshift clumpy discs and bulges in cosmological simulations. Mon. Not. R. Astron. Soc. 404, 2151–2169 (2010).

    ADS  Google Scholar 

  21. Genel, S., Dekel, A. & Cacciato, M. On the effect of cosmological inflow on turbulence and instability in galactic discs. Mon. Not. R. Astron. Soc. 425, 788–800 (2012).

    Article  ADS  Google Scholar 

  22. Gabor, J. M. & Bournaud, F. Delayed star formation in high-redshift stream-fed galaxies. Mon. Not. R. Astron. Soc. 437, L56–L60 (2014).

    Article  ADS  Google Scholar 

  23. Agertz, O. & Kravtsov, A. V. On the interplay between star formation and feedback in galaxy formation simulations. Astrophys. J. 804, 18 (2015).

    Article  ADS  Google Scholar 

  24. Straatman, C. M. S. et al. The FourStar Galaxy Evolution Survey (ZFOURGE): ultraviolet to far-infrared catalogs, medium–bandwidth photometric redshifts with improved accuracy, stellar masses, and confirmation of quiescent galaxies to z∼3.5. Astrophys. J. 830, 51 (2016).

    Article  ADS  Google Scholar 

  25. Daddi, E. et al. CO excitation of normal star-forming galaxies out to z = 1.5 as regulated by the properties of their interstellar medium. Astron. Astrophys. 577, A46 (2015).

    Article  Google Scholar 

  26. Bolatto, A. D. et al. High-resolution imaging of PHIBSS z ∼ 2 main-sequence galaxies in CO J = 1–0. Astrophys. J. 809, 175 (2015).

    Article  ADS  Google Scholar 

  27. Aravena, M. et al. CO(1–0) line imaging of massive star-forming disc galaxies at z=1.5–2.2. Mon. Not. R. Astron. Soc. 442, 558–564 (2014).

    Article  ADS  Google Scholar 

  28. Casey, C. M., Narayanan, D. & Cooray, A. Dusty star-forming galaxies at high redshift. Phys. Rep. 541, 45–161 (2014).

    Article  ADS  Google Scholar 

  29. Carilli, C. L. & Walter, F. Cool gas in high-redshift galaxies. Annu. Rev. Astron. Astrophys. 51, 105–161 (2013).

    Article  ADS  Google Scholar 

  30. Scoville, N. et al. ISM masses and the star formation law at z=1 to 6: ALMA observations of dust continuum in 145 galaxies in the COSMOS survey field. Astrophys. J. 820, 83 (2016).

    Article  ADS  Google Scholar 

  31. Persson, S. E. et al. FourStar: the near-infrared imager for the 6.5 μm Baade telescope at Las Campanas Observatory. Publ. Astron. Soc. Pacif. 125, 654–682 (2013).

    Article  ADS  Google Scholar 

  32. Grogin, N. A. et al. CANDELS: the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey. Astrophys. J. Suppl. Ser. 197, 35 (2011).

    Article  ADS  Google Scholar 

  33. Koekemoer, A. M. et al. CANDELS: the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey — the Hubble Space Telescope observations, imaging data products, and mosaics. Astrophys. J. Suppl. Ser. 197, 36 (2011).

    Article  ADS  Google Scholar 

  34. Tomczak, A. R. et al. Galaxy stellar mass functions from ZFOURGE/CANDELS: an excess of low-mass galaxies since z = 2 and the rapid buildup of quiescent galaxies. Astrophys. J. 783, 85 (2014).

    Article  ADS  Google Scholar 

  35. Mutch, S. J., Croton, D. J. & Poole, G. B. The mid-life crisis of the Milky Way and M31. Astrophys. J. 736, 84 (2011).

    Article  ADS  Google Scholar 

  36. Moster, B. P., Naab, T. & White, S. D. M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 428, 3121–3138 (2013).

    Article  ADS  Google Scholar 

  37. van Dokkum, P. G. et al. The assembly of Milky-Way-like galaxies since z∼2.5. Astrophys. J. 771, L35 (2013).

    Article  ADS  Google Scholar 

  38. Wellons, S. & Torrey, P. An improved probabilistic approach for linking progenitor and descendant galaxy populations using comoving number density. Preprint at https://arxiv.org/abs/1606.07815 (2016).

  39. Vanzella, E. et al. The Great Observatories Origins Deep Survey. VLT/FORS2 spectroscopy in the GOODS-South field: part III. Astron. Astrophys. 478, 83–92 (2008).

    Article  ADS  Google Scholar 

  40. Kriek, M. et al. An ultra-deep near-infrared spectrum of a compact quiescent galaxy at z = 2.2. Astrophys. J. 700, 221–231 (2009).

    Article  ADS  Google Scholar 

  41. Tomczak, A. R. et al. The SFR-M* relation and empirical star-formation histories from ZFOURGE* at 0.5 &lt; z &lt; 4. Astrophys. J. 817, 118 (2016).

    Article  ADS  Google Scholar 

  42. Elbaz, D. et al. GOODS-Herschel: an infrared main sequence for star-forming galaxies. Astron. Astrophys. 533, A119 (2011).

    Article  Google Scholar 

  43. Magnelli, B. et al. Evolution of the dusty infrared luminosity function from z = 0 to z = 2.3 using observations from Spitzer. Astron. Astrophys. 528, A35 (2011).

    Article  Google Scholar 

  44. Magnelli, B. et al. The deepest Herschel-PACS far-infrared survey: number counts and infrared luminosity functions from combined PEP/GOODS-H observations. Astron. Astrophys. 553, A132 (2013).

    Article  Google Scholar 

  45. Berta, S. et al. PEP Full Public Data Release (DR1): PACS Data (Max Planck Institute, 2013); http://irsa.ipac.caltech.edu/data/Herschel/PEP/docs/readme%5FPEP%5Fglobal.pdf

  46. Lutz, D. et al. PACS Evolutionary Probe (PEP) — a Herschel key program. Astron. Astrophys. 532, A90 (2011).

    Article  Google Scholar 

  47. Rieke, G. H. et al. Determining star formation rates for infrared galaxies. Astrophys. J. 692, 556–573 (2009).

    Article  ADS  Google Scholar 

  48. Chary, R. & Elbaz, D. Interpreting the cosmic infrared background: constraints on the evolution of the dust-enshrouded star formation rate. Astrophys. J. 556, 562–581 (2001).

    Article  ADS  Google Scholar 

  49. Dale, D. A. et al. Infrared spectral energy distributions of nearby galaxies. Astrophys. J. 633, 857–870 (2005).

    Article  ADS  Google Scholar 

  50. Howell, J. H. et al. The Great Observatories All-sky LIRG Survey: comparison of ultraviolet and far-infrared properties. Astrophys. J. 715, 572–588 (2010).

    Article  ADS  Google Scholar 

  51. McMullin, J. P., Waters, B., Schiebel, D., Young, W. & Golap, K. CASA architecture and applications. In Astronomical Data Analysis Software and Systems XVI (eds Shaw, R. A., Hill, F. & Bell, D. J ) 127 (Astronomical Society of the Pacific Conference Series, 2007).

    Google Scholar 

  52. Daddi, E. et al. Different star formation laws for disks versus starbursts at low and high redshifts. Astrophys. J. 714, L118–L122 (2010).

    Article  ADS  Google Scholar 

  53. Bolatto, A. D., Wolfire, M. & Leroy, A. K. The CO-to-H 2 conversion factor. Annu. Rev. Astron. Astrophys. 51, 207–268 (2013).

    Article  ADS  Google Scholar 

  54. Feldmann, R., Gnedin, N. Y. & Kravtsov, A. V. The X-factor in galaxies. I: dependence on environment and scale. Astrophys. J. 747, 124 (2012).

    Article  ADS  Google Scholar 

  55. Narayanan, D., Krumholz, M. R., Ostriker, E. C. & Hernquist, L. A general model for the CO–H 2 conversion factor in galaxies with applications to the star formation law. Mon. Not. R. Astron. Soc. 421, 3127–3146 (2012).

    Article  ADS  Google Scholar 

  56. Genzel, R. et al. The metallicity dependence of the CO−H 2 conversion factor in z &gt; 1 star-forming galaxies. Astrophys. J. 746, 69 (2012).

    Article  ADS  Google Scholar 

  57. Pérez-Montero, E. et al. Physical properties of galaxies and their evolution in the VIMOS VLT Deep Survey. II. Extending the mass–metallicity relation to the range z ∼ 0.89–1.24. Astron. Astrophys. 495, 73–81 (2009).

    Article  ADS  Google Scholar 

  58. Zahid, H. J., Kewley, L. J. & Bresolin, F. The mass–metallicity and luminosity–metallicity relations from DEEP2 at z ∼ 0.8. Astrophys. J. 730, 137 (2011).

    Article  ADS  Google Scholar 

  59. Stott, J. P. et al. A fundamental metallicity relation for galaxies at z = 0.84–1.47 from HiZELS. Mon. Not. R. Astron. Soc. 436, 1130–1141 (2013).

    Article  ADS  Google Scholar 

  60. Chabrier, G. Galactic stellar and substellar initial mass function. Publ. Astron. Soc. Pacif. 115, 763–795 (2003).

    Article  ADS  Google Scholar 

  61. Planck Collaboration, Planck 2015 results. XIII: Cosmological parameters. Astrophys. Astron. 594, A13 (2016).

  62. Riess, A. G. et al. A 24% determination of the local value of the Hubble constant. Astrophys. J. 826, 56 (2016).

  63. Gao, Y. & Solomon, P. M. The star formation rate and dense molecular gas in galaxies. Astrophys. J. 606, 271–290 (2004).

    Article  ADS  Google Scholar 

  64. Combes, F. et al. Galaxy evolution and star formation efficiency at 0.2 &lt; z &lt; 0.6. Astron. Astrophys. 528, A124 (2011).

    Article  Google Scholar 

  65. Combes, F. et al. Gas fraction and star formation efficiency at z &lt; 1.0. Astron. Astrophys. 550, A41 (2013).

    Article  Google Scholar 

Download references

Acknowledgements

The authors thank their colleagues on the CANDELS and ZFOURGE surveys for providing high quality data. The authors also thank the ALMA staff for facilitating the observations and aiding in the calibration and reduction process. The authors acknowledge generous support from the Mitchell Institute for Fundamental Physics and Astronomy at Texas A&M University. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.01234.S. ALMA is a partnership of the European Southern Observatory (representing its member states), the National Science Foundation (USA) and the National Institutes of Natural Sciences (Japan), together with the National Research Council (Canada), the National Science Council and the Academia Sinica Institute of Astronomy and Astrophysics (Taiwan) and the Korea Astronomy and Space Science Institute (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by the European Southern Observatory, Associated Universities, Inc./National Radio Astronomy Observatory and the National Astronomical Observatory of Japan. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

Author information

Authors and Affiliations

  1. George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, College Station, 78743, Texas, USA

    C. Papovich, R. Quadri & K.-V. Tran

  2. Department of Physics and Astronomy, Texas A&M University, 4242 TAMU, College Station, 78743, Texas, USA

    C. Papovich, R. Quadri & K.-V. Tran

  3. Leiden Observatory, Leiden University, PO Box 9513, Leiden, 2300 RA, The Netherlands

    I. Labbé & C. Straatman

  4. Centre for Astrophysics & Supercomputing, Swinburne University, Hawthorn, 3122, Victoria, Australia

    K. Glazebrook, G. Bekiaris & D. Fisher

  5. National Optical Astronomy Observatory, Tucson, 85719, Arizona, USA

    M. Dickinson & H. Inami

  6. Department of Astronomy, The University of Texas at Austin, 2515 Speedway, Stop C1400, Austin, 78712, Texas, USA

    S. L. Finkelstein & R. C. Livermore

  7. Centre de Recherche Astrophysique de Lyon, Université de Lyon, Université Lyon 1, CNRS, Observatoire de Lyon, 9 avenue Charles André, Saint-Genis Laval Cedex, F-69561, France

    H. Inami

  8. Department of Physics & Astronomy, Macquarie University, Sydney, 2109, New South Wales, Australia

    L. Spitler

  9. Australian Astronomical Observatory, PO Box 915, North Ryde, 1670, New South Wales , Australia

    L. Spitler

Authors
  1. C. Papovich
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Labbé
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Glazebrook
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. Quadri
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. G. Bekiaris
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. M. Dickinson
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. S. L. Finkelstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. D. Fisher
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. H. Inami
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. R. C. Livermore
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. L. Spitler
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. C. Straatman
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. K.-V. Tran
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

C.P. led the ALMA observing programme, handled the data reduction and led the writing of the manuscript. I.L., K.G., R.Q., L.S., C.S. and K.-V.T. contributed extensively to the ZFOURGE data set, used in much of the analysis. S.L.F., D.F. and R.C.L. contributed to the design of the ALMA observing programme and assisted in the reduction and interpretation of the ALMA data. G.B. and K.G. assisted in the interpretation of the ALMA data. M.D. and H.I. carried out the data analysis of the Spitzer and Herschel imaging. All coauthors contributed to the writing of the manuscript and to the ALMA observing programme.

Corresponding author

Correspondence to C. Papovich.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Tables 1-2, Supplementary Figures 1–4 (PDF 322 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Papovich, C., Labbé, I., Glazebrook, K. et al. Large molecular gas reservoirs in ancestors of Milky Way-mass galaxies nine billion years ago. Nat Astron 1, 0003 (2017). https://doi.org/10.1038/s41550-016-0003

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1038/s41550-016-0003

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing