Absence of emergent supersymmetry at superconducting quantum critical points in Dirac and Weyl semimetals

Abstract

Supersymmetry plays a crucial role in superstring theory and high-energy physics, but has never been observed in experiments. Recently, an effective space–time supersymmetry (SUSY) was argued to emerge in the low-energy region by tuning Dirac or Weyl semimetal to approach a superconducting (SC) quantum critical point (QCP), at which the Dirac or Weyl fermion and the bosonic order parameter are both massless. Here, we study under what circumstances can SUSY be realized at a quantum critical point. We demonstrate that the Yukawa-type coupling between the massless fermion and massless boson can dynamically generate an infinite number of non-supersymmetric terms in the effective field theory of the boson. Owing to these terms, no space–time supersymmetry emerges at the SC QCPs. The results provide important constraint on the exploration of emergent SUSY in condensed matter systems.

Introduction

Space–time supersymmetry (SUSY) is known to be the only nontrivial combination of the space–time and internal symmetries.^1,2 It transforms fermions into bosons, and vice versa. SUSY provides a possible solution to hierarchy problem.^1,2,3,4,5 Gravity is naturally obtained if SUSY is local in space and time. Owing to many fantastic features, SUSY has been extensively studied in high-energy physics for half a century. Unfortunately, there is so far no experimental evidence for SUSY, and it remains unclear whether or not SUSY is a fundamental law of nature.

Although the search for SUSY in high-energy processes has reached basically nothing, a variety of condensed matter systems were conjectured to manifest emergent SUSY at low energies.^{6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23} At the microscopic level, these systems are non-supersymmetric, and even non-relativistic. As the energy is lowered down to zero, the systems can flow to a stable fixed point at which the Lorentz symmetry is respected.^24,25 Under certain circumstances, there might emerge an effective space–time SUSY. The emergence of SUSY could provide an opportunity to explore the intriguing predictions of SUSY theories in condensed matter systems. However, it is technically difficult to realize effective SUSY in actual materials, as one usually needs to delicately tune two or even more parameters.

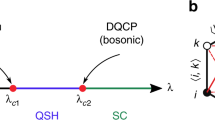
Quantum critical system is an ideal platform to probe emergent SUSY. A prominent example is the quantum critical point (QCP) between Dirac semimetal (SM) phase and uniform superconducting (SC) phase on the surface of three-dimensional (3D) topological insulator.¹⁵ The Dirac fermion is massless (gapless) in the SM phase due to the peculiar electronic structure, and becomes massive (gapped) in the SC phase due to Cooper pairing. The SC order parameter can be described by a composite boson, which is massive (gapped) in the SM phase. As the system is tuned to exactly the QCP, both the fermion and boson are strictly massless. Renormalization group (RG) analysis^9,15 argued that the model of such a QCP flows to a stable infrared fixed point that respects an effective space–time SUSY at low energies. An attractive feature of this proposal is that SUSY is realized by tuning one single parameter, which is technically more feasible than previously studied models. SUSY was also predicted to emerge when a Dirac/Weyl SM undergoes quantum phase transition to the pair-density-wave (PDW) state.^17,23 A universal characteristic of these models is that the boson arises from some sort of fermion pairing.

Realizing space–time SUSY at large distances (low energies) in quantum critical systems that are non-supersymmetric at small distances is a fascinating notion. This might allow us to employ the powerful methods developed in the studies of supersymmetric quantum field theories^1,2 to investigate the striking quantum critical phenomena. However, before ascertaining the existence of emergent SUSY in any realistic quantum critical system, we must first make sure that all the potential SUSY-breaking effects are absent at low energies.

For effective SUSY to emerge, the low-energy field theory of QCP must contain a number of massless fermions and an equal number of bosons. The fermion–boson interaction is described by the Yukawa-type coupling. From previous research experiences of non-relativistic QCPs^{26,27,28,29,30} with dynamical exponents z = 2 and z = 3, we have learned that the fermion–boson coupling may lead to certain type of infrared singularity at ultra-low energies in case both fermions and bosons are massless (gapless). The infrared singularity may prevent SUSY from emerging at low energies. For the Dirac and Weyl SMs considered in this work, the dynamical exponent is z = 1. We will perform a generic, model-independent field-theoretic analysis of the Yukawa coupling between massless fermion and massless boson, and demonstrate that SUSY cannot emerge if the Yukawa coupling generates nonlocal self-coupling terms of the boson field. Based on this result, we establish a necessary condition for space–time SUSY to emerge at any QCP. This condition is universally applicable and imposes an important constraint to the exploration of emergent SUSY in condensed matter systems.

Results

Model

Although our analysis is entirely model independent, here for concreteness we first consider a specific model to illustrate our strategy. The generalization to other models is straightforward. In particular, we choose to start from the following action

$$S = {\int} d \tau d^{d}r[i\bar \psi \partial \psi + |\partial _\mu \phi |^{2} + \lambda _4|\phi |^{4} + g(\phi^{\ast} \psi^{T}i\sigma _{2}\psi + {\mathrm{h}}.{\mathrm{c}}.)],$$

(1)

where τ is imaginary time and $\partial$ = γ_μ∂_μ. The γ-matrices are defined via the Pauli matrices σ_i as follows: γ₀ = σ₃, γ₁ = σ₁, and γ₂ = σ₂. This action can be regarded as an effective theory for SM–SC QCP.²⁰ The boson field ϕ represents the SC order parameter, whereas the spinor field ψ, whose conjugate is $\bar \psi = - i\psi ^\dagger \gamma _0$, stands for the Dirac fermion. According to RG study,²⁰ fermion and boson velocities can be taken to be equal, i.e., v_f = v_b. The strength parameter for Yukawa coupling is g, and that for |ϕ|⁴ coupling is λ₄. When the system is deep in the SM phase, there are only fermionic degrees of freedom, namely Dirac fermion. As the system is tuned to approach the QCP towards SC order, composite bosons emerge as a result of Cooper pairing. At the QCP, both the fermion and the boson are exactly massless and equally important at low energies. The Yukawa coupling between them determines the quantum critical behaviors.^26,27,28 Three-loop RG analysis performed by Zerf et al.²⁰ indicates that this model has a stable infrared fixed point $g^{ \ast 2} = \lambda _4^ \ast$, at which the action (1) is invariant under the following SUSY transformations

$$\delta _{\eta} \psi = i\partial \phi^{\ast} \eta - \frac{1}{2}\phi^{2}i\sigma _{2}\bar \eta^{T},\quad \delta_{\eta} \phi = - \bar \psi \eta ,$$

(2)

$$\delta _{\eta} \bar \psi = i\bar \eta\partial \phi - \frac{1}{2}\phi ^{\ast 2}\eta ^{T}i\sigma _{2},\quad \delta _\eta \phi ^{\ast} = \bar \eta \psi ,$$

(3)

where η is a two-component Grassmann variable introduced to define the transformations.

Infrared singularities

To examine whether SUSY emerges, it is necessary to carry out perturbative RG analysis of Eq. (1). Although the boson originates from fermion pairing, the coupling constants λ₄ and g could flow independently with varying energy scale. In the low-energy limit, if the system flows to a stable infrared fixed point $(g^ \ast ,\lambda _4^ \ast )$ satisfying the condition $g^{ \ast 2} = \lambda _4^ \ast$, SUSY emerges. This is the strategy adopted in previous studies on emergent SUSY.^9,15,20 However, all the previous RG studies are based on an assumption that the |ϕ|⁴ term is always a smooth function of momentum vector q = (q₀, q). This assumption is valid only when the |ϕ|⁴ term does not receive any singular quantum correction from the Yukawa coupling. In Fig. 1a, we show the one-loop diagram for the correction to |ϕ|⁴ term. In case the contribution of this diagram is singular (non-analytic) in q, the low-energy properties of the λ₄|ϕ|⁴ term would be dominated by the singular correction, and the total |ϕ|⁴ term would become nonlocal. The nonlocal |ϕ|⁴ term does not respect SUSY.

Fig. 1

Feynman diagrams for the vertex corrections. a Diagram for the vertex correction to |ϕ|⁴ term. b Diagram for the vertex correction to a generic |ϕ|²ⁿ term with n > 2. The solid (dashed) line represents the free fermion (boson) propagator

Apart from |ϕ|⁴ term, the Yukawa coupling also produces an infinite number of higher order terms |ϕ|²ⁿ, where the integer n > 2. The corresponding diagram is given by Fig. 1b. In previous works on emergent SUSY,^{9,15,17,20,23} all of such |ϕ|²ⁿ terms were naively supposed to be irrelevant and thus were simply ignored. But there is no guarantee that these terms are irrelevant at QCP. Indeed, we will show below that all of these terms are marginal at low energies. The key point is that, the Yukawa coupling induces singular corrections to λ₄ and as such alters the scaling dimension of the boson field ϕ. Once this fact is taken into account, all the nonlocal |ϕ|²ⁿ terms with n > 2 are important at low energies.

We infer from the above analysis that SUSY emerges only when the following condition is fulfilled: the Yukawa coupling does not lead to any nonlocal |ϕ|²ⁿ term. If one or more |ϕ|²ⁿ terms are generated, SUSY is absent.

In the following, we calculate the coefficients of |ϕ|²ⁿ terms with n ≥ 1, and then make a scaling analysis to verify whether these SUSY-breaking terms are relevant, marginal, or irrelevant. Our analysis starts from the local action given by Eq. (1), which is formally similar to, but not the same as, the models studied in refs. ^{9,14,15,17,23}. It is straightforward to apply our model-independent analysis to models defined at any dimension and made out of any type of fermion (Dirac or Weyl).

As the first step, we compute the diagrams of Fig. 1a, b. The loop integral contains a number of free fermion propagators. When the fermion is massive (gapped), the integral is free of infrared singularity, as the mass provides an infrared cutoff that regularizes the small energy/momenta contributions. But as the fermion is massless at the QCP, the integral might be severely divergent in the infrared region. One should compute the loop integral carefully. According to action (1), the free fermion propagator is G₀(k) = 1/k. The vertex correction presented in Fig. 1a is defined as

$$\begin{array}{c}\lambda _4(q_1,q_2,q_3) = g^4 {\int\frac{{d^Dp}}{{(2\pi )^D}}} {\mathrm{Tr}}\left[ {G_0(p)\sigma _2G_0^T( - p - q_1)\sigma _2G_0(p + q_1 + q_2)\sigma _2} \right.\\ \left. { \times G_0^T( - p - q_1 - q_2 - q_3)\sigma _2} \right],\end{array}$$

(4)

where the space–time dimension D = d + 1 and we have used the fact that q₄ = −q₁ − q₂ − q₃. The vertex function depends on three independent external momenta, namely q₁, q₂, and q₃. It is difficult to get an analytic expression. Fortunately, the possible singularity comes mainly from very small external momenta.^26,27 This fact allows us to assume that q₁ = q₂ = q₃ = q. Carrying out analytical calculations, we obtain

$$\lambda _4(q,q,q) \propto \frac{{g^4}}{{|q|}}$$

(5)

in D = 2 + 1 with a positive constant prefactor and $|q| = \sqrt {q_0^2 + {\mathbf{q}}^2}$, and

$$\lambda _4(q,q,q) \propto g^4\ln \left( {\frac{{|q|}}{\Lambda }} \right)$$

(6)

in D = 3 + 1, where Λ is an ultraviolet cutoff. Apparently, λ₄(q, q, q) is singular as q → 0.

The loop diagram Fig. 1a was calculated in previous works^9,15,17,20 by means of standard RG method. Although the models considered in these works are physically different, the loop integrals have the same structure and can be computed universally. No singular contribution was found in the calculations of refs. ^9,15,17,20. That no singular behavior was obtained in their works originates from the treatment that all the external boson momenta were directly set to zero.^9,15,17,20 We emphasize here that this treatment is questionable. Notice that the dominant contributions to diagram Fig. 1a come from the processes in which the internal fermion momenta p are smaller than the external boson momenta q, i.e., processes with |p| < |q|. If all the external boson momenta are naively forced to vanish, these contributions would be entirely discarded. In order not to miss the contributions from the fermionic modes carrying ultra-low momenta, the external boson momenta should be kept finite. As shown in Eqs. (5) and (6), the coupling parameter λ₄ becomes singular once such contributions are carefully taken into account, which makes the |ϕ|⁴ term nonlocal.

Numerical simulations^21,22 have been performed to calculate correlation functions at some SM–SC QCPs, claiming to find evidence of emergent SUSY. The particle momenta obtained in numerical simulations are discrete, thus a large part of the ultra-low-energy/momenta region cannot be accessed in numerical simulations. This indicates that the SUSY-breaking nonlocal terms are actually invisible in numerical data. Therefore, although numerical simulations could obtain interesting information on the correlation functions at intermediate energies, their resolution is not high enough to unambiguously determine whether an exact space–time SUSY is respected in the ultra-low-energy region. Moreover, in the strict sense SUSY is an extension of the Poincaré space–time symmetry.^1,2 When a model system is defined on finite lattices,^21,22 both the continuous translational symmetry and Lorentz symmetry are broken. To judge whether exact space–time SUSY emerges in the lowest energy limit, it is necessary to directly study continuum quantum field theories and carry out careful field-theoretic analysis.

Previous studies have demonstrated^{26,27,28,29,30} that the quantum critical fluctuations of order parameters may induce nonlocal terms in some non-relativistic metals with dynamical exponent larger than unity (z > 1). This behavior is related to the existence of an infinite number of gapless fermionic excitations on the finite Fermi surface. For instance, such a coupling produces highly nonlocal terms at the QCP between d = 2 normal metal and antiferromagnet.²⁷ Different from these examples, the fermion density of states (DOS) vanishes at the Dirac/Weyl point of the SM–SC QCP studied in this work. However, the vanishing of fermion DOS cannot be used to preclude nonlocal terms. The reason is that the particle momenta q cannot be always fixed at zero: q should be allowed to take both zero and nonzero values. No matter how small the boson momenta q is, there are always an infinite number of fermionic modes below the energy scale of |q|, which inevitably gives rise to the infrared singularity of λ₄(q).

After showing that |ϕ|⁴ term becomes nonlocal due to Yukawa coupling, we next consider the |ϕ|²ⁿ terms with n > 2. For this purpose, we need to compute the diagram Fig. 1b. The coupling parameter for |ϕ|²ⁿ terms is formally given by

$$\begin{array}{c}\lambda _{2n} = g^{2n} {\int\frac{{d^Dp}}{{(2\pi )^D}}} {\mathrm{Tr}}\left[ {\sigma _2G_0(p)\sigma _2G_0^T( - p - q_1)\sigma _2...} \right.\\ \left. { \times G_0\left( {p + \mathop {\sum}\limits_{i = 1}^{2n - 2} {q_i} } \right)\sigma _2G_0^T\left( { - p - \mathop {\sum}\limits_{i = 1}^{2n - 1} {q_i} } \right)} \right]\end{array}$$

(7)

where for notational simplicity the explicit dependence of λ_2n on external momenta is omitted. We adopt the same simplification as what we have done in the computation of λ₄, and set all the external momenta to be equal. Under this approximation, we obtain

$$\lambda _{2n} \propto g^{2n}\left( {\frac{1}{{q^2}}} \right)^{n - \frac{D}{2}}.$$

(8)

Strictly speaking, this expression is applicable only for n ≠ D/2. However, as our aim is to determine the scaling behavior of the self-coupling vertices, it can be written in this form for any n and D. Detailed calculation of λ_2n is presented in the Supplementary Information. It is easy to observe that the coupling parameter λ_2n also becomes singular, and that the singularity is more severe for larger n.

Importance of nonlocal terms

On the basis of λ₄(q) and λ_2n(q), we next make a scaling analysis to determine whether the nonlocal |ϕ|²ⁿ terms are relevant, marginal, or irrelevant. Incorporating the generated nonlocal terms into the original action (1), we now re-write the effective total action as follows

$$S = S_f^0 + S_b^0 + S_I + S_b,$$

(9)

$$S_f^0 = {\int} {\frac{{d^Dp}}{{(2\pi )^D}}} \bar \psi (p)\gamma \cdot p\psi (p),$$

(10)

$$S_b^0 = {\int} {\frac{{d^Dk}}{{(2\pi )^D}}} k^2\phi ^\dagger (k)\phi (k),$$

(11)

$$S_I = {\int} {\frac{{d^Dp}}{{(2\pi )^D}}} \frac{{d^Dk}}{{(2\pi )^D}}g\left[ {\psi ^T(p)i\sigma _2\psi (k)\phi (k - p) + h.c.} \right],$$

(12)

$$S_b = \mathop {\sum}\limits_{n = 1}^\infty {u_{2n}} \left( {{\int} {\frac{{d^Dk}}{{(2\pi )^D}}} } \right)^{2n - 1}(k^2)^{\frac{D}{2} - n}|\phi (k)|^{2n},$$

(13)

where $u_{2n} \propto g^{2n}/v_f^d$. Using the scaling dimension in momentum space, we have

$$\left[ {p_0} \right] = z,\,\left[ {\mathbf{p}} \right] = 1,\,\left[ {v_f} \right] = \left[ {v_b} \right] = z - 1,\,\left[ p \right] = \left[ {\sqrt {p_0^2 + v_{f,b}^2{\mathbf{p}}^2} } \right] = z.$$

(14)

Here, z is the dynamical exponent for both the fermionic and bosonic fields.

Within the standard RG framework,³¹ one usually takes the free action $S^0 = S_f^0 + S_b^0$ as the free fixed point, which reproduces itself upon making RG transformations, and then determines the scaling behaviors of all the field operators and coupling constants. In the present case, it is easy to find the following scaling behaviors:

$$\left[ {\psi (p)} \right] = - \frac{{2z + d}}{2},\quad \left[ {\phi (k)} \right] = - \frac{{3z + d}}{2},$$

$$\left[ g \right] = \frac{{3z - d}}{2},\quad \left[ {u_{2n}} \right] = (3z - d)n + d(1 - z).$$

(15)

According to Eq. (8), for n = 1 we see that the one-loop polarization function behaves as

$${\mathrm{{\Pi}}}_2(k) \propto g^2\left( {k^2} \right)^{\frac{D}{2} - 1},$$

(16)

which means that z = 1 is not changed by adding the polarization to the free boson action. As pointed out in refs. ^32,33 that z is not altered by higher order corrections results from the U(1) gauge invariance²⁰ of action (1). In the case of z = 1, it is clear that [u_2n] = 0 for d = 3, thus all the |ϕ|²ⁿ terms are marginal. For d < 3, [u_2n] > 0 and there are an infinite number of relevant self-coupling terms. This indicates that, at the QCP of d < 3 system, the one-loop polarization Π₂(k) is more important than the free boson action given by Eq. (9) in the ultra-low-energy region. As a result, it is no longer appropriate to regard the free boson action $S_b^0$ as the free fixed point. A more suitable approach is to adopt the scheme proposed in refs. ^33,34: discard the free boson action $S_b^0$, and determine the scaling dimension of boson field ϕ by taking the Yukawa coupling, i.e., S_I, as the starting fixed point. Employing this scheme, we find the following correct scaling dimensions:

$$\left[ {\psi (p)} \right] = - \frac{{2z + d}}{2},\quad \left[ {\phi (k)} \right] = - d,\quad \left[ g \right] = 0,\quad \left[ {u_{2n}} \right] = d(1 - z).$$

(17)

For z = 1, all the |ϕ|²ⁿ terms with n ≥ 2 are marginal. This conclusion is independent of the spatial dimension. An immediate indication is that all the bosonic self-coupling terms are equally important at low energies and should be considered simultaneously.

We then discuss the impact of nonlocal |ϕ|⁴ and |ϕ|²ⁿ terms on the fate of emergent SUSY. In the absence of nonlocal terms, the action given by Eq. (1) is a well-defined local quantum field theory. All the |ϕ|²ⁿ terms with n > 2 are irrelevant, and can be simply ignored. RG calculations²⁰ confirm that the system flows to a stable infrared fixed point at which an effective SUSY emerges. This conclusion, however, is fundamentally changed once nonlocal terms are generated. As all the |ϕ|²ⁿ terms with n ≥ 2 are marginal, the simple action (1) is not the correct low-energy theory of SM–SC QCP. Actually, after incorporating the marginal nonlocal terms into action (1), the SM–SC QCP does not exhibit emergent SUSY.

Discussion

In supersymmetric field theories, there is a non-renormalization theorem,^1,2 which ensures that loop integrals are free of divergences. This theorem cannot be used to eliminate the infrared singularities induced by the Yukawa coupling in quantum critical systems. This is because the non-renormalization theorem is applicable only in the special case in which the system respects the intrinsic SUSY at the most microscopic level. However, emergent SUSY refers to an effective SUSY that is realized only at very-low energies but is apparently absent at high energies (small distances). To avoid infrared singularities, one could construct a lattice model that respects space–time SUSY at the tree (classic) level. Nonlocal terms would not exist in such a model owing to the non-renormalization theorem. To realize this type of lattice model, one has to delicately tune two or more model parameters,¹¹ which is certainly difficult.

Now suppose the boson appearing in Eq. (1) is not made out of fermion pairing. This sort of boson has its own dynamics. Can SUSY emerge at large distances in such a system that is non-supersymmetric at small distances? The answer is negative, as the Yukawa coupling still induces nonlocal quantum correction to each self-coupling term |ϕ|²ⁿ with n ≥ 2. The system does not respect SUSY at the microscopic level, thus one cannot invoke the non-renormalization theorem to prevent nonlocal corrections. The nonlocal corrections dominate over the original local terms at low energies, and all the |ϕ|²ⁿ terms are marginal. We therefore conclude that nonlocal terms prevent SUSY no matter whether or not the boson arises from fermion pairing.

Our consideration is general for continuous quantum phase transitions and independent of the specific model to achieve the transition. As a concrete example, we have showed that the model described action (1) does not exhibit emergent SUSY owing to nonlocal |ϕ|²ⁿ terms. The condition can be easily extended to other similar models. Here, we mention two kinds of models. The first kind is the SM–SC QCP realized on the surface of 3D topological insulator.^14,15,20 This QCP can be described by the effective action (1). The second kind is defined by the QCP between Dirac/Weyl SM and PDW,¹⁷ which involves two Dirac/Weyl points. In this case, the effective action can be regarded as two copies of Eq. (1) along with an additional coupling between two types of bosons. Although the PDW order parameter carries a finite momentum,^35,36 we confirmed that the Yukawa coupling also induces nonlocal terms at the SM-PDW QCP. Thus, no SUSY emerges in the above two kinds of models.

In conclusion, we have revealed a necessary condition for space–time SUSY to emerge in a microscopically non-supersymmetric system: no nonlocal self-coupling terms of the boson field are induced by the Yukawa coupling. This provides an important guidance to the search of emergent SUSY in condensed matter systems. Because the Yukawa coupling between massless fermion and massless boson often leads to nonlocal terms, it is not legitimate to seek emergent SUSY at QCPs. Instead, one should consider fully gapped systems. For instance, one might try to tune the system away from the QCP to enter into the ordered phase such that both the fermion mass m_f and the boson mass m_b are finite.¹⁵ If the distance to QCP took certain suitable value, the two masses could be equal,²¹ namely m_f = m_b. In such a special case, nonlocal terms are absent and in principle there might be effective SUSY. However, this equal-mass state is fragile: once the distance to QCP is changed, there is no chance for SUSY to emerge.

Experiments can be performed to judge whether SUSY is respected. In case the system described by action Eq. (1) respects space–time SUSY, the anomalous dimensions for fermion and boson fields are equal and given by³⁷ η_ψ = η_ϕ = 1/3. As a result, the fermionic DOS behaves as ρ(ω) ∝ ω^4/3 at the QCP. In addition, SUSY would lead to an exact result for the zero-temperature optical conductivity¹⁹ $\sigma \left( {\omega ,T = 0} \right) = \frac{{5\left( {16\pi - 9\sqrt 3 } \right)}}{{243\pi }}\frac{{e^2}}{\hbar }$. These two quantities can be measured in experiments. As our analysis found that nonlocal terms prevent space–time SUSY from emerging, we predict that the above signatures of SUSY would not be observed. Recent experiments have reported the discovery of intrinsic superconductivity on the surface of a 3D topological insulator Sb₂Te₃,³⁸ which allows one to experimentally test whether SUSY really emerges at the SM–SC QCP.

The physical impact of nonlocal |ϕ|²ⁿ terms is to be fully understood. Such terms play a dominant role in the low-energy region, as their prefactors diverge as the lowest energy limit is taken. The QCP becomes unstable owing to these terms. Such an instability could be avoided by two possible scenarios. Firstly, the phase transition may become first order.³⁹ At a first order transition, the boson field ϕ develops a finite vacuum expectation value abruptly, rather than continuously. In this case, the boson mass m_b is always finite and there are no nonlocal terms. This scenario can be experimentally explored by measuring latent heat and change of specific volume. Second, the quantum fluctuation of bosonic order parameter may induce a new type of ordered phase, which substitutes the putative unstable QCP at low temperatures. At sufficiently high temperatures, the new order is destroyed, and the Yukawa coupling does not generate nonlocal terms but leads to intriguing quantum critical phenomena characterized by finite anomalous dimensions of fermion and boson fields.¹⁵ This picture is analogous to the one in which the strong nematic quantum critical fluctuation around a nematic QCP induces long-range SC order at low temperatures and non-Fermi-liquid behavior at high temperatures.^40,41 For both of the two scenarios, no space–time SUSY emerges at the transition. The model-independent analysis presented in this work is not sufficient to judge which scenario is the actual one, because the answer might sensitively depend on the spatial dimensionality, the nature of the fermion field, and the property of the bosonic order parameter. Further investigations are called for to determine which scenario works at a given QCP.

Methods

The nonlocal |ϕ|²ⁿ terms are obtained by calculating the Feynman diagrams presented in Fig. 1 using standard methods of quantum field theory. In order not to miss such nonlocal terms, the external boson momenta are kept finite. The calculational details of Eqs. (4) and (7) can be found in the Supplementary Information. The (ir)relevance of nonlocal |ϕ|²ⁿ terms in the low-energy region is investigated by making a scaling analysis of the effective action given by Eqs. (9–13). The scaling dimensions of the fermion field, the boson field, and all the coupling constants (i.e., g and u_2n) are determined by taking the Yukawa coupling term, rather than the free action, as the free fixed point.