Enhanced nematic fluctuations near an antiferromagnetic Mott insulator and possible application to high-T_c cuprates

Abstract

Motivated by the widespread experimental observations of nematicity in strongly underdoped cuprate superconductors, we investigate the possibility of enhanced nematic fluctuations in the vicinity of a Mott insulator that displays Néel-type antiferromagnetic order. By performing a strong-coupling expansion of an effective model that contains both Cu-d and O-p orbitals on the square lattice, we demonstrate that quadrupolar fluctuations in the p-orbitals inevitably generate a biquadratic coupling between the spins of the d-orbitals. The key point revealed by our classical Monte-Carlo simulations and large-N calculations is that the biquadratic term favors local stripe-like magnetic fluctuations, which result in an enhanced nematic susceptibility that onsets at a temperature scale determined by the effective Heisenberg exchange J. We discuss the impact of this type of nematic order on the magnetic spectrum and outline possible implications on our understanding of nematicity in the cuprates.

Introduction

Hole-doped cuprates are susceptible to a variety of different types of electronic order in the underdoped regime. Examples include tendencies toward charge order,^1,2,3,4 which becomes long-ranged in the presence of large magnetic fields,^1,4 and tendencies toward nematic order,^5,6,7,8,9,10 characterized by the breaking of the tetragonal symmetry of the system.^11,12 The fact that these tendencies appear in the region of the phase diagram where a pseudogap is also observed (see schematic Fig. 1) suggest a close interplay between these seemingly different phenomena, a topic that remains widely debated in the field (for recent reviews, see^13,14).

Fig. 1

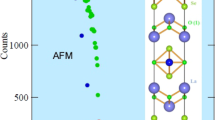
Microscopic manifestation of nematic fluctuations. a Schematic phase diagram of hole-doped cuprate superconductors. b The microscopic model we use contains a Cu $3d_{x^2 - y^2}$ orbital (center orbital) and O 2p_x and 2p_y orbitals in a single unit cell. The hopping parameters are given by t_pd, t_pp, and interactions are considered on-site U_dd, U_pp, and between nearest-neighbors V_pd, V_pp. c Simple illustration that nematic fluctuations induce a short-ranged magnetic stripe ordered region (light red) within a Néel ordered background (yellow). This snapshot is taken from our classical Monte-Carlo simulations. Red and blue color of the arrows denote out-of-the-plane components of the spins

Although the microscopic mechanisms behind these different ordering tendencies, and particularly of nematicity, remain unsettled, they have been the subject of many different theoretical proposals (see, for instance,^{15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30} and also the reviews^11,12). While a complete theory for nematicity in the cuprates is beyond the scope of our work, here we show that an important contribution to the nematic susceptibility arises already near the Mott (or more precisely, charge-transfer³¹) insulating state of the parent compound. For the rest of the paper, thus, we focus only on the spin correlations near the Mott state, and neglect other phenomena that are certainly important for a complete description of the hole-doped cuprates, and which may also be important to describe nematicity, such as charge order, pseudogap, time-reversal symmetry-breaking, pair-density waves, and superconductivity.^13,14

To be more specific, we consider the so-called Emery model,³² an effective model that attempts to capture both Cu and O low-energy degrees of freedom by introducing $d_{x^2 - y^2}$ orbitals on the sites of the square lattice and p_x (p_y) orbitals on the horizontal (vertical) bonds. Consider first the case where only d-orbitals are present. In the half-filled Mott insulating state, the charge degrees of freedom are quenched, and the low-energy physics is described completely in terms of an AFM Heisenberg interaction J between the d-orbital spins, which ultimately gives rise to a Néel AFM ground state. Upon light hole-doping, the effective Hamiltonian is known as the t–J model:³³

$$H_{t - J} = \mathop {\sum}\limits_{ij\alpha } {\kern 1pt} t_{ij}\widetilde{d}_{i,\alpha }^\dagger \widetilde{d}_{j,\alpha} + J\mathop {\sum}\limits_{\left\langle {ij} \right\rangle } \left( {{\bf{S}}_i \cdot {\bf{S}}_j - \frac{1}{4}n_in_j} \right).$$

(1)

Here, t_ij denotes the hole hopping parameters and J the AFM exchange coupling. The operator ${\bf{S}}_{i} = \frac{1}{2}\mathop {\sum}\nolimits_{\alpha \beta } {\kern 1pt} \widetilde{d}_{i,\alpha }^{\dagger} {\boldsymbol{\sigma }}_{\alpha \beta }\widetilde{d}_{i,\beta }$ describes the d-orbital spin and $n_{i} = \mathop {\sum}\nolimits_\alpha {\kern 1pt} \widetilde{d}_{i,\alpha }^{\dagger} \widetilde{d}_{i,\alpha }$ the corresponding charge. The strong local Coulomb interaction is incorporated in terms of the hole creation operator $\widetilde{d}_{i,\alpha }^{\dagger} = \left( {1 - n_{i\bar \alpha }} \right)d_{i,\alpha }^{\dagger}$, reflecting the fact that double occupancy of the sites is not allowed near the Mott insulating state.

As we demonstrate below via a strong-coupling expansion of the Emery model, the inclusion of the p-orbitals leads to an important additional term in the t–J Hamiltonian. While the two terms in Eq. (1) remain the same, albeit with a different microscopic expression for J, noncritical quadrupolar fluctuations of the p-orbitals, enhanced by the repulsion between p-orbitals, generate a positive biquadratic coupling K > 0 between the d-orbital spins:

$$H_K = - K\mathop {\sum}\limits_i \left[ {{\bf{S}}_i \cdot \left( {{\bf{S}}_{i - \hat x} + {\bf{S}}_{i + \hat x} - {\bf{S}}_{i - \hat y} - {\bf{S}}_{i + \hat y}} \right)} \right]^2,$$

(2)

resulting in an effective t−J−K Hamiltonian, H_t−J−K = H_t−J + H_K.

Using classical Monte-Carlo and large-N analytical methods, we find that the main consequence of H_K is to enhance the static electronic nematic susceptibility χ_nem near the AFM-Mott insulating state. However, χ_nem is not found to diverge on its own—instead, it peaks at a temperature scale proportional to J, instead of K. The location of the peak depends on the relative strength of quantum and thermal fluctuations and shifts towards smaller temperatures for larger quantum fluctuations. As illustrated in Fig. 1c, the enhancement of nematic fluctuations promoted by H_K has its origins in the short-ranged magnetic stripe ordered regions that this term favors within the (much longer ranged) Néel ordered background. Consequently, within the t−J−K model, the onset of nematic order requires an additional symmetry-breaking field that can take advantage of the enhanced susceptibility. While a more detailed discussion of the application of these results to the cuprates is left to the end of this paper, we note that this mechanism for enhanced nematic susceptibility can in principle be combined with other mechanisms proposed in the literature to yield long-range nematic order. Detailed reviews on the proposed mechanisms for nematicity in cuprates, both within weak and strong-coupling regimes, can be found for instance in refs. ^11,12.

Results

Microscopic model

Our starting point is the interacting three-orbital Emery model H = H₀ + H_U + H_V.³² As depicted in Fig. 1b, it includes the $d_{x^2 - y^2}$ Cu orbital with creation operator $d_{i,\sigma }^\dagger$ at Bravais lattice position R_i and spin σ as well as the p_x and p_y O orbitals with creation operators $p_{i + \frac{{\hat x}}{2},\sigma }^\dagger$ and $p_{i + \frac{{\hat y}}{2},\sigma }^\dagger$. The noninteracting part H₀ includes hopping between p-orbitals with (amplitude t_pp) and between d- and p-orbitals (with amplitude t_pd). The corresponding sign factors of the hopping elements follow from the phases of the orbitals (see Fig. 1b).³² In addition, H₀ contains on-site terms where the energy difference between Cu and O orbitals is given as Δ = ε_p − ε_d. Interactions are included on-site $H_U = U_{dd}\mathop {\sum}\nolimits_i {\kern 1pt} n_{i, \uparrow }^dn_{i, \downarrow }^d$ + $\frac{{U_{pp}}}{2}\mathop {\sum}\nolimits_{i,u} {\kern 1pt} n_{i + u, \uparrow }^pn_{i + u, \downarrow }^p$ with $u \in \left\{ {\frac{{\hat x}}{2},\frac{{\hat y}}{2}} \right\}$, and number operators $n_{i,\sigma }^d = d_{i,\sigma }^\dagger d_{i,\sigma }$ and $n_{i + u,\sigma }^p = p_{i + u,\sigma }^\dagger p_{i + u,\sigma }$. We also consider nearest-neighbor interactions $H_V = \frac{{V_{pp}}}{2}\mathop {\sum}\nolimits_{i,u,u^\prime } {\kern 1pt} n_{i + u}^pn_{i + u + u^\prime }^p$ + $V_{pd}\mathop {\sum}\nolimits_{i,u} n_i^dn_{i + u}^p$ with $u^\prime \in \left\{ { \pm \frac{1}{2}\left( {\hat x + \hat y} \right), \pm \frac{1}{2}\left( {\hat x - \hat y} \right)} \right\}$ and $n_i^d = \mathop {\sum}\nolimits_\sigma n_{i,\sigma }^d$, $n_{i + u}^p = \mathop {\sum}\nolimits_\sigma n_{i + u,\sigma }^p$.

The largest energy scales are the local repulsion U_dd between d-orbitals and the charge-transfer energy Δ (with U_dd much larger than Δ), suggesting a strong-coupling expansion in small $t_{ij} \ll {\mathrm{\Delta }},U_{dd} - {\mathrm{\Delta }}$. This yields a description in terms of localized d-orbital spins S_i coupled to mobile p-orbital holes. An expansion up to fourth order in the hopping term t_pd was performed in refs ^34,35. There appear Kondo-like exchange couplings $\propto {\boldsymbol{S}}_i \cdot {\boldsymbol{s}}_{i + u_1,i + u_2}$ between the d- and p-orbital spin-densities ${\boldsymbol{s}}_{i + u_1,i + u_2} = \frac{1}{2}\mathop {\sum}\nolimits_{\tau ,\tau ^\prime } {\kern 1pt} p_{i + u_1,\tau }^\dagger {\boldsymbol{\sigma }}_{\tau \tau ^\prime }p_{i + u_2,\tau ^\prime }$,³⁶ the familiar Heisenberg spin exchange term $J\mathop {\sum}\nolimits_{\langle i,j\rangle } {\kern 1pt} {\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_j$ and terms that renormalize the p-orbital hole dispersion. For details we refer to the Methods section and the Supplementary Information. The Kondo-like terms also modify the hole dispersion as the tunneling process of holes through a d-orbital becomes spin dependent. For example, tunneling through a background of Néel ordered d-orbital spins leads to the spin dependent hopping parameters $t_a = \frac{{t_{pd}^2}}{2}\left( {\frac{1}{{\mathrm{\Delta }}} + \frac{3}{{U_{dd} - {\mathrm{\Delta }}}}} \right)$ and $t_b = \frac{{t_{pd}^2}}{2}\left( {\frac{3}{{\mathrm{\Delta }}} + \frac{1}{{U_{dd} - {\mathrm{\Delta }}}}} \right)$ for holes with spin parallel and antiparallel to the central d-orbital spin.²⁴ The hole Fermi surface thus appears at momenta ${\boldsymbol{k}} = \left( { \pm \frac{\pi }{2}, \pm \frac{\pi }{2}} \right)$ for small doping n_p.

Most notably for our considerations, the strong-coupling expansion also yields a spin exchange term that depends on the occupation of the intermediate p-orbital between d-orbital sites:

$$H_{J^\prime } = - J^{\prime} \mathop {\sum}\limits_{i,\delta } {\kern 1pt} n_{i + \frac{\delta }{2}}^p{\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_{i + \delta }$$

(3)

where $\delta \in \left\{ { \pm {\hat x}, \pm {\hat y}} \right\}$ and the spin exchange coupling constant is given by $J^{\prime} = \mathop {\sum}\nolimits_{n = 0}^{3} \frac{{t_{pd}^{4}{\mathrm{sign}}\left( {3 \,-\, 2n} \right)}}{{{\mathrm{\Delta }}^{3 - n}\left( {U_{dd} \,-\, {\mathrm{\Delta }}} \right)^n}}$. Note that $J = \mathop {\sum}\nolimits_{n = 0}^2 \frac{{t_{pd}^4\left( {4 \,-\, n^2 \,-\, \delta _{n,2}} \right)}}{{2{\mathrm{\Delta }}^{3-n}\left( {U_{dd} \,-\, {\mathrm{\Delta }}} \right)^n}}$ and in the large-U_dd limit both are of the same order J′/J → 1/2. Oxygen charge fluctuations thus not only renormalize the Heisenberg exchange via the Kondo coupling terms, but, as we show now, also lead to the biquadratic spin exchange interaction K in Eq. (2).

We derive the biquadratic exchange K by first decomposing the p-orbital densities as $n_{i + \frac{{\hat x}}{2}}^p = n_i^p + \eta _i$ and $n_{i + \frac{{\hat y}}{2}}^p = n_i^p - \eta _i$, where η_i is the quadrupolar (nematic) component of the oxygen charge density.²¹ The combination of on-site and nearest-neighbor Coulomb interactions between p-orbital leads to a term $\left( { - 2{\sum} {\kern 1pt} U_{\boldsymbol{k}}\eta _{\boldsymbol{k}}\eta _{ - {\boldsymbol{k}}}} \right)$ in the Hamiltonian, where $U_{\boldsymbol{k}} = \frac{1}{4}\left( {V_{pp}{\mathrm{Re}}{\kern 1pt} f_{\boldsymbol{k}} - \frac{{U_{pp}}}{2}} \right)$ and $f_{\boldsymbol{k}} = 1 + e^{ - ik_x} + e^{ik_y} + e^{i\left( {k_y - k_x} \right)}$. Integrating out the quadrupolar charge fluctuations associated with the p-orbitals (details of this analysis are presented in the Methods section and the Supplementary Information) yields the result for the biquadratic exchange interaction in Eq. (2) with:

$$K = \frac{{J^{\prime 2}}}{2}\frac{{{\int}_{\bf{k}} {\kern 1pt} {\mathrm{{\Pi}}}_{\bf{k}}^\eta }}{{1 - \left( {V_{pp} - \frac{{U_{pp}}}{8}} \right){\mathrm{{\Pi}}}_{{\bf{k}} = 0}^\eta }} \,>\, 0.$$

(4)

Here, ${\mathrm{{\Pi}}}_{\bf{k}}^\eta = - {\int}_{{\bf{q}},\omega^\prime} {\kern 1pt} {\mathrm{Tr}}\left[ {G_{{\bf{q}},{\it{\omega }}^\prime }^p\left( {\tau ^z\sigma ^0s^0} \right)G_{{\bf{q}} + {\bf{k}},\omega ^\prime }\left( {\tau ^z\sigma ^0s^0} \right)} \right]$ is the bare p-orbital charge susceptibility in the quadrupolar (i.e., nematic) channel. We have used the long-wavelength approximation in the denominator for simplicity (the full expression can be found in the Supplementary Information and yields qualitatively identical results). The Pauli matrices τ^j, s^j and σⁱ act in orbital (p_x, p_y), spin and reduced wavevector (k, k + (π, π)) space, respectively. Note that the presence of the AF background of d-orbital spins leads to a doubling of the unit cell, and thus ${\int}_{\boldsymbol{q}} \equiv {\int}_{{\mathrm{mBZ}}} \frac{{d^2q}}{{2\pi ^2}}$ is an integration over the magnetic Brillouin zone (mBZ). Explicit expressions for the p-orbital Green’s functions $G_{{\bf{q}},\omega }^p$ are given in the Methods section and the Supplementary Information and yield

$${\mathrm{{\Pi}}}_{\boldsymbol{k}}^\eta = - {\int}_{\boldsymbol{q}} {\kern 1pt} \mathop {\sum}\limits_{i,j = 1}^4 \frac{{v_{ij;{\boldsymbol{q}},{\boldsymbol{q}} + {\boldsymbol{k}}}\left\{ {n_F\left( {\xi _{i,{\boldsymbol{q}}}} \right) - n_F\left( {\xi _{j,{\boldsymbol{q}} + {\boldsymbol{k}}}} \right)} \right\}}}{{\epsilon _{i,{\boldsymbol{q}}} - \epsilon _{j,{\boldsymbol{q}} + {\boldsymbol{k}}}}}$$

(5)

with $\epsilon _{i,{\boldsymbol{q}}}$ being the renormalized p-orbital dispersion and $\xi _{i,{\boldsymbol{q}}} = \epsilon _{i,{\boldsymbol{q}}} - \mu$ with the chemical potential μ. The matrix elements $v_{ij;{\boldsymbol{q}},{\boldsymbol{q}} + {\boldsymbol{k}}} = W_{\boldsymbol{q}}^\dagger \left( {\tau ^z\sigma ^0} \right)W_{{\boldsymbol{q}} - {\boldsymbol{k}}}$ contain W_q, which are unitary matrices that transform between orbital/reduced k-space (σⁱ ⊗ τ^j) and band space. Most importantly, Eq. (4) makes it clear that the biquadratic exchange K in Eq. (2) is a direct consequence of quadrupolar oxygen charge fluctuations. This is a generic feature of the model and exist even if the p-orbital holes are not dressed by d-orbital spins.

The oxygen quadrupolar susceptibility ${\mathrm{{\Pi}}}_{\boldsymbol{k}}^\eta$ (and thus K) is strictly positive for all k and is determined by the occupation number difference between the different oxygen bands. In the relevant regime of small hole fillings $n_p \ll 1$, the response approaches a value ${\mathrm{{\Pi}}}_{{\boldsymbol{k}} = 0}^\eta \propto n_p$ at low T, peaks around T ≈ |μ| and vanishes as 1/T at large T. The response increases for smaller bandwidth, e.g., smaller t_pp. This is derived explicitly in the Supplementary Information for a simpler two-band model that neglects the interaction with the AF background. It also holds true numerically for the full four-band model, as shown in Fig. 2a, where we present results for the renormalized quadrupolar response ${\tilde{\mathrm {\Pi}}}_{{\boldsymbol{k}} = 0}^\eta = \frac{1}{2}\left[ {\left( {{\mathrm{{\Pi}}}_{{\bf{k}} = 0}^\eta } \right)^{ - 1} - U_{{\boldsymbol{k}} = 0}} \right]^{ - 1}$ and for the resulting K/J within the microscopic four-band model. In the calculation we keep n_d = 1, assuming that holes are doped into the p-orbitals, but we take the interaction of the mobile holes with the AF background of d-orbital spins fully into account. We clearly observe that a large nearest-neighbor repulsion V_pp and a small bandwidth t_pp enhance K (see Eq. (4)). Our results also indicate that an enhancement of the quadrupolar density fluctuations by V_pp is necessary for a significant biquadratic exchange coupling. This follows from K/J ∝ (J′²/J)(n_p/t_pp) at small n_p where J′ = 0.08, J = 0.15 for the parameters in Fig. 2. Finally, while phonon modes in the same channel are, by symmetry, allowed to give rise to similar behavior, the electronic mechanism for biquadratic exchange is expected to be quantitatively much stronger.

Fig. 2

Strength of biquadratic exchange K within Emery model and enhanced nematic spin fluctuations. a Renormalized quadrupolar oxygen density response function ${\tilde{\mathrm {\Pi}}}_{{\boldsymbol{k}} = 0}^\eta = \frac{1}{2}\left[ {\left( {{\mathrm{{\Pi}}}_{{\boldsymbol{k}} = 0}^\eta } \right)^{ - 1} - U_{{\boldsymbol{k}} = 0}} \right]^{ - 1}$ as a function of p-orbital holes n_p (per planar d-orbital) obtained within the three-band Emery model at low temperature T = 10⁻²t_pp and fixed n_d = 1. The interaction of the mobile holes with the antiferromagnetic Néel background of d-orbital spins is fully taken into account. Other parameters are set to t_pd = 1, Δ = 2.5, U_dd = 11, and V_pd = V_pp such that $U_{{\boldsymbol{k}} = 0} = V_{pp} - \frac{{U_{pp}}}{8}$. We use U_pp = 5.5 for V_pp = 5.5 and U_pp = 4.5 for all other values of V_pp. Amplitude of oxygen quadrupolar fluctuations increases with V_pp and smaller oxygen bandwidth, e.g., smaller t_pp. The inset shows the resulting value of K/J ∝ (J′²/J)(n_p/t_pp) (at small n_p) from which we conclude that an enhancement of the fluctuations by V_pp is crucial for a significant biquadratic exchange coupling. Note that we have approximated ${\mathrm{{\Pi}}}_{\boldsymbol{k}}^\eta \approx {\mathrm{{\Pi}}}_{{\boldsymbol{k}} = 0}^\eta$ for simplicity, which does not affect our conclusion. b, c show the static nematic susceptibility χ_nem in Eq. (7) for the H_t−J−K model of Eq. (2) at half-filling as a function of temperature T obtained by Monte-Carlo simulations of classical spins. A non-zero K enhances the response in the nematic B_1g channel only. Inset phase diagram shows that we are investigating χ_nem above the Néel ordered state. For consistency with the known spin-wave spectrum, we consider a small ferromagnetic next-nearest-neighbor exchange J₂ = −0.1J

Enhanced nematic susceptibility

The implications of H_K can be better understood in the limit of K > J. In this case, the AFM ground state is no longer the Néel configuration with ordering vector Q = (π, π), but the striped configuration with Q = (π, 0) or (0, π). While the limit of large K/J is clearly not realized in the cuprates, it reveals that H_K supports quantum and classical fluctuations with local striped-magnetic order that have significant statistical weight.

We qualitatively demonstrate this behavior in Fig. 1c by showing typical spin configurations of a Monte-Carlo analysis of H_t–J–K in the limit of classical spins and where the kinetic energy of the holes is ignored. One clearly sees local striped-magnetic fluctuations (light red background) in an environment of Néel ordered spins (yellow background). Configurations with parallel spins along the x-axis and along the y-axis occur with equal probability, hence preserving the tetragonal symmetry of the system. If one, however, weakly disturbs tetragonal symmetry, e.g., by straining one of the axes, this balance is disturbed and one favors striped configurations of one type over the other.

The behavior described above can be quantified in terms of the composite spin variable:

$$\varphi _i = {\bf{S}}_i \cdot \left( {{\bf{S}}_{i - \hat x} + {\bf{S}}_{i + \hat x} - {\bf{S}}_{i - \hat y} - {\bf{S}}_{i + \hat y}} \right)$$

(6)

which changes sign under a rotation by π/2. Note that the square of this term, which appears in Eq. (2), is invariant under this transformation, and therefore is fully consistent with the fourfold symmetry of the Emery model. While 〈φ_i〉 = 0 for realistic values of K (and in the absence of external strain), the static nematic susceptibility

$$\chi _{{\mathrm{nem}}}\left( T \right) = {\int}_0^{1/T} {\kern 1pt} d\tau \mathop {\sum}\limits_i \left\langle {{\cal T}_\tau \varphi _i\left( \tau \right)\varphi _0\left( 0 \right)} \right\rangle$$

(7)

is a measure for the increased relevance of local stripe magnetic configurations. Here, ${\cal T}_\tau$ denotes imaginary time ordering.

We present a quantitative demonstration that the biquadratic exchange K yields an enhanced nematic susceptibility in the B_1g (x² − y²) symmetry channel in Fig. 2b, c. It contains Monte-Carlo results for χ_nem for a collection of classical Heisenberg spins that interact according to the H_J–K model. For consistency with the known spin-wave spectrum, we have included an additional small second-neighbor exchange J₂ = −0.1J in the simulation. One clearly sees that the biquadratic term K enhances the nematic response in the B_1g channel, corresponding to an inequivalence between the x- and y-axes. In the limit of classical spins, the nematic susceptibility χ_nem(T) is nonmonotonic, peaking at a temperature governed by the effective exchange interaction of the spins, T_nem ~ J, which is independent on K.

The Monte-Carlo results also display that χ_nem(T → 0) → 0, which is a consequence of the classical nature of the spins in the simulations and a resulting absence of (thermal) fluctuations in the zero temperature limit. Quantum fluctuations crucially modify this behavior and lead to χ_nem(T → 0) > 0. This is demonstrated in Fig. 3, where we present results of an analytical calculation of the nematic response χ_nem that includes the effect of quantum fluctuations within a soft-spin field-theoretical version of the spin degrees of freedom in Eq. (2). After decoupling the biquadratic exchange term K in the nematic channel and taking the long-wavelength limit, which is appropriate to study the low-energy excitations, we obtain the effective action:

$$\begin{array}{*{20}{l}} S \hfill & = \hfill & {S_{{\mathrm{dyn}}} + {\int}_r \left[ {\left( {\nabla {\bf{n}}_r} \right)^2 \,-\, \varphi _r\left( {\left( {\partial _x{\bf{n}}_r} \right)^2 \,-\, \left( {\partial _y{\bf{n}}_r} \right)^2} \right)} \right]} \hfill \\ {} \hfill & {} \hfill & { \,+\, {\int}_r \left[ {r_0{\bf{n}}_r^2 + \frac{u}{2}\left( {{\bf{n}}_r \cdot {\bf{n}}_r} \right)^2 + \frac{{\varphi _r^2}}{{2g}} - h_r\varphi _r} \right]} \hfill \end{array}$$

(8)

where n_r is the N = 3 component staggered Néel order parameter, as used in the nonlinear sigma model of refs. ^37,38. The parameter r₀ controls the distance to the AFM Néel quantum-critical point located at r_0,c. For δr₀ ≡ r₀ − r_0,c < 0, the system has long-range AFM order at T = 0, whereas for δr₀ > 0 it is in the paramagnetic phase (see sketches at the bottom of Fig. 3), and the interaction parameters are g ∝ K/J > 0, u > g. The integrations are over ${\int}_r \equiv {\int}_0^{1/T} {\kern 1pt} d\tau {\int} {\kern 1pt} d^2r$, where r = (τ, r) combines imaginary time τ and position r = (x, y). In addition, φ_r is the nematic order parameter of Eq. (6) and h_r is an external strain field. The quantum dynamics of the Néel order parameter is governed by $S_{{\mathrm{dyn}}} = {\int}_q {\kern 1pt} f\left( {\omega _n} \right){\bf{n}}_q \cdot {\bf{n}}_{ - q}$, where $f\left( {\omega _n} \right) \propto \omega _n^2$ at half filling, while f(ω_n) = γ|ω_n| was proposed to describe particle-hole excitations, and will be used below as we describe the system away from half-filling n_p > 0. Here, q = (ω_n, q) combines Matsubara frequency ω_n and momentum q (measured relative to the AFM ordering vector Q = (π, π)) and ${\int}_q \equiv T\mathop {\sum}\nolimits_n {\int} \frac{{d^2q}}{{\left( {2\pi } \right)^2}}$.

Fig. 3

Nematic susceptibility including quantum fluctuations. Effects of quantum fluctuations are included in the analytical treatment of a soft-spin field theory of the H_J–K model. a shows the bare nematic susceptibility $\chi _{{\mathrm{nem}}}^{(0)}(\xi ,T)$ (normalized to its T = 0 value) as a function of temperature T, right above the Néel QCP r₀ = r_0,c (see inset). Different curves correspond to different functional behavior of the Néel correlation length ξ(T)⁻² = aγT. The nonuniversal constant a determines whether $\chi _{{\mathrm{nem}}}^{(0)}$ peaks at T = 0 (a > π) or at finite T (a < π). Thus, $\chi _{{\mathrm{nem}}}^{(0)}$ can exhibit different shapes in different systems, as expected for a nonuniversal susceptibility, which remains finite at the AFM QCP. b, c contain results of a large-N treatment of the model, which allows an explicit solution of ξ(T, δr₀). Dashed (solid) lines are for g = 0 (g = 0.1), where g ∝ K/J. b is for fixed distances to the QCP δr₀ = {−r_0,c, 0, r_0,c} (green, yellow, red; as indicated in the sketch below) and varying T. Quantum fluctuations render the susceptibility at T = 0 finite, but have no strong effect on the finite temperature behavior. Importantly, nonzero biquadratic exchange g > 0 enhances the finite temperature nematic response and increases the maximal value of χ_nem around T ~ Λ²/γ ~ J (with momentum cutoff Λ = 10 and frequency cutoff γΛ_ω = 100). c is for fixed temperatures γT/Λ² = {0, 0.1, 0.2} (blue, purple, magenta) and varying δr₀. It demonstrates that the nematic response increases with the magnetic correlation length, as the system approaches the QCP. The quartic coefficient is set to u/γ = 50 in (b) and u/γ = 5 in (c)

The nematic susceptibility in Eq. (7) can be obtained for general N and reads (see Methods section and Supplementary Information):

$$\chi _{{\mathrm{nem}}} = \frac{{\chi _{{\mathrm{nem}}}^{\left( {\mathrm{0}} \right)}}}{{1 - \frac{g}{N}\chi _{{\mathrm{nem}}}^{\left( {\mathrm{0}} \right)}}},$$

(9)

where the bare nematic susceptibility is given by $\chi _{{\mathrm{nem}}}^{\left( 0 \right)} = \frac{N}{2}{\int}_q \frac{{\left| {\boldsymbol{q}} \right|^4{\mathrm{cos}}^2(2\theta )}}{{\left( {\xi ^{ - 2} \,+\, \left| {\boldsymbol{q}} \right|^2 \,+\, f\left( {\omega _n} \right)} \right)^2}}$ with q = |q|(cos θ, sin θ). Here, ξ is the magnetic correlation length for Néel order, that includes interaction corrections and diverges at the AFM phase transition. Right above the quantum-critical point at δr₀ = 0, one finds ξ⁻² = aγT with nonuniversal constant a. As shown in Fig. 3a, the exact shape of $\chi _{{\mathrm{nem}}}^{(0)}(T)$ depends on this nonuniversal parameter a, which depends, for example, on the interaction parameter u or the lattice constant. While $\chi _{{\mathrm{nem}}}^{(0)}$ peaks at finite temperatures for a < π, which is similar to the classical case, the maximum occurs at T = 0 for a > π. Note that nematic correlations remain finite ranged at the AFM quantum-critical point and universal behavior of $\chi _{{\mathrm{nem}}}^{(0)}$ is not guaranteed (in contrast to the AFM susceptibility, which is universal). Being a nonuniversal quantity, we thus expect that the precise shape of $\chi _{{\mathrm{nem}}}^{(0)}$ can be different for different systems.

In order to make analytic progress and calculate a(u), or more generally ξ(T, δr₀), we consider the limit of large N. This approach led to important insights in both the description of antiferromagnetic correlations of the cuprate parent compounds³⁸ and of nematic fluctuations of iron-based superconductors.³⁹ The magnetic correlation length ξ is determined self-consistently within large-N for a given distance to the AFM quantum-critical point δr₀. Despite the similarity between Eq. (9) and the expression for the nematic susceptibility of iron-based superconductors,³⁹ there are very important differences between the two systems. Because the iron-pnictides order magnetically in a striped configuration, $\chi _{{\mathrm{nem}}}^{\left( 0 \right)}$ diverges when ξ → ∞, which guarantees that a nematic transition takes place already in the paramagnetic state for any g > 0. However, because our model orders in a Néel configuration, $\chi _{{\mathrm{nem}}}^{\left( 0 \right)}$ remains finite even when ξ → ∞. Although long-range nematic order is not present, nematic fluctuations can be significantly enhanced if the biquadratic exchange K ∝ g is sufficiently large.

In Fig. 3b, c, we show the nematic susceptibility obtained within the large-N approach (see Methods section and Supplementary Information). Like in the Monte-Carlo results (see Fig. 2), we observe, in Fig. 3b, a broad maximum at finite temperatures around T ≈ J, corresponding at δr₀ = 0 to a < π. The lattice cutoff Λ plays the role of J in the continuum model. The effect of g, and thus of the biquadratic exchange K, is to enhance the amplitude of the peak (comparing dashed and solid lines). The pronounced peak of χ_nem originates from the bare susceptibility $\chi _{{\mathrm{nem}}}^{\left( 0 \right)}$. As discussed above, the bare response is in turn governed by the magnetic correlation length ξ that is set by T/J. Notably, at low temperatures, quantum fluctuations render χ_nem (and $\chi _{{\mathrm{nem}}}^{(0)}$) finite, in stark contrast to our MC results for classical spins. Keeping T fixed and varying the non-thermal tuning parameter δr₀, we observe in Fig. 3c that the nematic response increases for an increasing magnetic correlation length, i.e., Néel fluctuations enhance the nematic susceptibility. This follows from the observation that χ_nem(δr₀, T) is an increasing function for decreasing δr₀.

Consequences of long-range nematic order

As we discussed above, the nematic susceptibility does not diverge within our H_J–K model. Nevertheless, it is interesting to study what happens to the magnetic spectrum if nematic order is induced—either by the presence of a small tetragonal-symmetry breaking field h, which can induce a sizable nematic order parameter φ ≈ χ_nemh, or by combination with other microscopic mechanisms for nematicity. From the action in Eq. (8), we can readily obtain the dynamic spin susceptibility in the presence of nematic order

$$\chi _{{\mathrm{AFM}}}\left( {{\bf{Q}} + {\bf{q}},\omega } \right) = \frac{1}{{\xi ^{ - 2} + {\bf{q}}^2 - \varphi \left( {q_x^2 - q_y^2} \right) + f\left( {\omega _n} \right)}},$$

(10)

Therefore, as shown in Fig. 4, nonzero φ modifies the spin–spin structure factor near the Néel ordering vector Q from a circular shape, which preserves tetragonal symmetry, to an elliptical shape, which breaks tetragonal symmetry. In addition, as φ increases, it shifts the maximum of χ_AFM(Q + q, ω) from the commensurate q = 0 value to an incommensurate wavevector q_IC ≠ 0, with q_IC parallel to either the x-axis (if φ > 0) or to the y-axis (if φ < 0). Note that a somewhat related mechanism for the incommensurate spin order, based on the t–J model, was reported in refs ^40,41,42. Previous works have also focused on nematicity arising from a pre-existing incommensurability,²⁸ whereas in our scenario incommensurate magnetic order is a consequence of nematic order, caused by an enhanced nematic susceptibility in the presence of an (external) symmetry-breaking field.

Fig. 4

Incommensurability transition induced by nematic order. a–c schematically illustrate the effect of finite nematic order φ on the spin–spin correlation function. It shows χ_AFM(k) from Eq. (10) (including a fourth order term ∝ q⁴) for ξ⁻² = 0.2 and φ = {0., 1., 1.5}. In the absence of nematic order (φ = 0) the magnetic susceptibility peak is isotropic around the Néel ordering vector Q = (π, π), but nonzero 0 < φ < 1 leads to an elliptic deformation of the peak. For larger values of φ > 1 the peak splits and two incommensurate scattering peaks emerge at (π ± δ, π). Note that, within our model, the inequivalence of x- and y-direction appears only in response to an external (or intrinsic) strain field that explicitly breaks C₄ symmetry

While these effects onset in the paramagnetic phase, the presence of nematic order should also be manifested in the Néel ordered state by the direction of the d-orbital moments, which would align parallel to either the x-axis or to the y-axis.⁴³ Within our model, we argue that such an effect would arise in the presence of spin–orbit coupling in the p-orbitals, which convert an imbalance in the charge of the p_x and p_y orbitals into a preferred direction for the d-orbital moment.

At first sight, one might anticipate that K would affect the spin-wave dispersion of the AFM Néel ground state.⁴⁴ As we show in the Supplementary Information, however, the biquadratic exchange of Eq. (2) does not modify the linearized classical spin-wave spectrum. The reason for this peculiar behavior is that the biquadratic exchange annihilates the classical Néel state, i.e., the vacuum of the linear spin-wave excitations:

$$H_K\left| {{\mathrm{N}}\mathop {{\mathrm{e}}}\limits^\prime {\mathrm{el}}} \right\rangle = 0{\kern 1pt} .$$

(11)

It is important to point out that all results discussed here were obtained considering that the spins of the H_J–K Hamiltonian are treated as vectors, either classical or in the large-N regime. It is interesting to ask what happens if one considers the quantum spin-1/2 case. It turns out that, for spin-1/2, the biquadratic term K > 0 transforms into an AFM next-nearest neighbor bilinear exchange coupling, which certainly changes the spin-wave spectrum. It remains an open question whether the results presented here remain unchanged if one performs this transformation from biquadratic to bilinear exchange in the microscopic model. Importantly, however, we note that a large AFM next-nearest neighbor exchange also favors a stripe magnetic state over a Néel state. Thus, the main ingredient that enhances the nematic susceptibility in the classical spin case seems also to be present in the spin-1/2 case.

Discussion

In summary, we showed via a strong-coupling expansion of the Emery model that quadrupolar charge fluctuations in the p-orbitals generate a biquadratic exchange coupling between the d-orbital spins, extending the celebrated t–J model employed to describe lightly-doped Mott insulators. The main effect of this biquadratic term is to enhance B_1g nematic fluctuations, which however is not translated into a diverging nematic susceptibility. Importantly, the temperature at which the nematic susceptibility onsets is determined not by the biquadratic coupling K, but by the standard nearest-neighbor exchange coupling J. The position of the peak is controlled by the relative strength of thermal versus quantum fluctuations, and moves from a temperature of order J for dominant thermal fluctuations toward zero for dominant quantum fluctuations. The biquadratic exchange K, however, sets the amplitude of the peak, and both increase for larger values of the repulsion V_pp between nearest-neighbor p-orbitals.

Thus, our main result is that magnetic correlations associated with the Mott insulating state generate an enhanced nematic susceptibility, which is driven by quadrupolar oxygen density fluctuations. In the remainder of this section, we discuss the possible applications of these results to the nematic tendencies observed in hole-doped cuprates.^11,12 The mechanism discussed here does not lead to long-range nematic order on its own. However, given the enhanced nematic susceptibility, it is expected that a small tetragonal symmetry-breaking field would lead to a sizable nematic order parameter. Such a symmetry-breaking field is naturally provided by the CuO chains or double chains in YBa₂Cu₃O_7−δ and YBa₂Cu₄O₈, respectively. Interestingly, in YBCO, several experimental observations are consistent with the existence of an electronic nematic order parameter.^5,6,7,10 Whether the observed nematicity is the result of the intrinsic small symmetry-breaking field combined with a large nematic susceptibility, or the consequence of true long-range order that would onset even if the chains were absent, remains to be determined.

Still in what concerns YBCO, it is interesting to note that nematic order is observed already at rather small doping levels, in the vicinity of the Mott insulating Néel state.^6,45 In this region of the phase diagram, where our results are the most relevant, the experimental nematic onset temperature is comparable to that of the Néel transition temperature, which in turn is set by J. Of course, since nematicity is not restricted only to the vicinity of the Néel state, it is possible that there are different mechanisms responsible for nematicity in different regions of the phase diagram.²⁸

Neutron scattering experiments in YBCO also reveal a strong feedback of nematic order on the magnetic spectrum.^6,43,45 In particular, nematic order is manifested as an elliptical spin structure factor centered at the Néel ordering vector. Upon lowering the temperature, the peak splits and gives rise to two unidirectional incommensurate peaks. These observations are qualitatively consistent with our results for the effect of nematicity on the AFM magnetic spectrum (see Fig. 4).

To further test the applicability of the effect discussed here on the physics of the cuprates, it would be desirable to directly measure the nematic susceptibility in tetragonal cuprates. In analogy to what has been done for the iron-pnictides (see ref. ⁴⁶), χ_nem is closely related to several observables, such as the elastoresistance,⁴⁷ the shear modulus, or electronic Raman scattering. If the biquadratic term found here was to govern the nematic properties of tetragonal cuprates, such as HgBa₂CuO₄, χ_nem should be enhanced but not divergent—possibly displaying a peak at a temperature comparable to J. Furthermore, the temperature dependences of χ_nem in the B_1g and B_2g channels would be similar, although the former would be larger.

Because the biquadratic term is the result of charge fluctuations on the oxygen p-orbitals, it is only present in the hole-doped side of the phase diagram, since electron-doping adds charge carriers directly to the Cu sites.⁴⁸ To the best of our knowledge, nematic tendencies have not been reported in electron-doped cuprates.¹¹ It would be interesting to verify this effect by experimentally determining χ_nem in tetragonal electron-doped systems, such as Nd₂CuO₄.

Methods

Derivation of t–J–K-model from microscopic three-band model

We derive the biquadratic K spin exchange term in Eq. (2) from a microscopic interacting three-band model H = H₀ + H_U + H_V that takes Cu $d_{x^2 - y^2}$ and O p_x, p_y orbitals into account and reads

$$\begin{array}{*{20}{l}} {H_0} \hfill & = \hfill & {\mathop {\sum}\limits_{i,\sigma } {\kern 1pt} {\mathrm{\Delta }}{\kern 1pt} n_{i\sigma }^{p} + t_{pd}\mathop {\sum}\limits_{\langle i,j\rangle } \left( {( - 1)^{u_{ij}}d_{i,\sigma }^{\dagger} p_{j,\sigma } + {\mathrm{h}}{\mathrm{.c}}{\mathrm{.}}} \right)} \hfill \\ {} \hfill & {} \hfill & { \,+\, t_{pp}\mathop {\sum}\limits_{\langle \langle i,j\rangle \rangle } \left( {( - 1)^{u_{ij}^\prime }p_{i,\sigma }^{\dagger} p_{j,\sigma } + {\mathrm{h}}{\mathrm{.c}}{\mathrm{.}}} \right)} \hfill \end{array}{,}$$

(12)

$$H_U = U_{dd}\mathop {\sum}\limits_i {\kern 1pt} n_{i \uparrow }^dn_{i \downarrow }^d + \frac{{U_{pp}}}{2}\mathop {\sum}\limits_i {\kern 1pt} n_{i \uparrow }^pn_{i \downarrow }^p{,}$$

(13)

$$H_V = V_{pd}\mathop {\sum}\limits_{\langle i,j\rangle } {\kern 1pt} n_i^dn_j^p + V_{pp}\mathop {\sum}\limits_{\langle \langle i,j\rangle \rangle } {\kern 1pt} n_i^pn_j^p.$$

(14)

Here, $d_{i,\sigma }^\dagger$ creates a hole in the $d_{x^2 - y^2}$ orbital at Bravais lattice site R_i, and $p_{i,\sigma }^\dagger$ creates a hole in the O p_x and p_y orbital $i \equiv {\boldsymbol{R}}_i + \frac{{{\hat{\boldsymbol x}}}}{2}$ and $i \equiv {\boldsymbol{R}}_i + \frac{{{\hat{\boldsymbol y}}}}{2}$, respectively (see Fig. 1b). The parameters in the Hamiltonian are the on-site orbital energy difference ${\mathrm{\Delta }} = \epsilon _p - \epsilon _d$, hoppings t_pp, t_pd (see Fig. 1), on-site interactions U_pp, U_dd and nearest-neighbor interactions V_pp, V_pd.

As U_dd is the largest energy scale, we perform a strong-coupling expansion which yields a description in terms of localized Cu-site spins S_i and mobile oxygen holes. The second-order terms contain direct O hopping terms and Cu–O Kondo coupling terms. We consider these terms in two complementary limits: (i) assuming an antiferromagnetically ordered background of Cu spins that renormalizes the oxygen bandstructure (main text) and (ii) disregarding both terms which yields a free oxygen dispersion (Supplementary Information). Both calculations yield qualitatively identical results for the quadrupolar response ${\tilde{\mathrm {\Pi}}}^\eta$ (see Fig. 2a) and biquadratic exchange K. To fourth order appears the Heisenberg exchange interaction term and the exchange interaction term in Eq. (3) that includes the density of the intermediate O orbital. Upon integrating out the O holes this term yields the biquadratic exchange K term of Eq. (2).

As the theory is quartic in O hole operators, we must first decouple the interaction terms. We perform the decoupling in the channel of the total and relative density of O atoms in a unit cell: $n_i^{p} = n_{i + \frac{{\hat x}}{2}}^{p} + n_{i + \frac{{\hat y}}{2}}^{p}$ and $\eta _i^{p} = n_{i + \frac{{\hat x}}{2}}^{p} - n_{i + \frac{{\hat y}}{2}}^{p}$. Introducing the vector $\nu _{\boldsymbol{k}} = \left( {n_{\boldsymbol{k}}^{p},\eta _{\boldsymbol{k}}^{p}} \right)^{T}$, where $n_i^{p} = \frac{1}{{N_L}}\mathop {\sum}\nolimits_{\boldsymbol{k}} {\kern 1pt} n_{\boldsymbol{k}}^{p}e^{i{\boldsymbol{k}} \cdot {\boldsymbol{R}}_i}$, the interaction terms read

$$H_{U_{pp}} + H_{V_{pp}} = - \mathop {\sum}\limits_{{\boldsymbol{k}};\,k_x > 0} {\kern 1pt} \nu _{\boldsymbol{k}}^{\dagger} U_{\boldsymbol{k}}^{ - 1}\nu _{\boldsymbol{k}}{,}$$

(15)

with interaction matrix

$$U_{\boldsymbol{k}}^{ - 1} = \frac{2}{{N_L}}\left( {\begin{array}{*{20}{c}} { - {\mathrm{Re}}\,{\kern 1pt} U_{ + ,{\boldsymbol{k}}}} & {\frac{{iV_{pp}}}{4}{\mathrm{Im}}{\kern 1pt} f_{\boldsymbol{k}}} \\ { - \frac{{iV_{pp}}}{4}{\mathrm{Im}}\,f_{\boldsymbol{k}}} & {{\mathrm{Re}}\,U_{ - ,{\boldsymbol{k}}}} \end{array}} \right){\kern 1pt} .$$

(16)

Here, $U_ \pm = \frac{1}{8}\left( {2V_{pp}f_{\boldsymbol{k}} \pm U_{pp}} \right)$ and $f_{\boldsymbol{k}} = 1 + e^{ - ik_x} + e^{ik_y} + e^{i\left( {k_y - k_x} \right)}$. We decouple the interactions using a Hubbard–Stratonovich (HS) transformation, which yields an action that is purely quadratic in O operators, but contains the HS fields Φ_k = (ψ_k, ϕ_k):

$$S = - {\int}_{q,q^\prime } \mathop {\sum}\limits_{\begin{array}{*{20}{c}} {\alpha,\alpha^\prime,\sigma,\sigma^\prime } \end{array}} {\kern 1pt} p_Q^\dagger G_{Q,Q^\prime }^{ - 1}p_{Q^\prime } + {\int}_q {\kern 1pt} {\mathrm{\Phi }}_q^\dagger U_q{\mathrm{\Phi }}_q.$$

(17)

Here, Q = (q, α, σ) combines the Matsubara frequency–momentum index q = (iq_n, q) with index α = x, y, which runs over the O orbital index p_x, p_y, and σ, which denotes spin. The Green’s function G⁻¹ contains the Cu spin operators due to the coupling term ∝ J′ in Eq. (3), the O hopping terms and the HS variables: $G^{ - 1} = G_0^{ - 1} + G_{\mathrm{\Phi }}^{ - 1} + G_{J^\prime }^{ - 1}$. It is diagonal in spin space, and is in orbital space (τ^α) given by

$$G_0^{ - 1}\left( {Q,Q^\prime } \right) = \left( {iq_n - {\mathrm{\Delta }} + \mu } \right)1 - t_{pp}{\mathrm{Re}}\left( {h_{\boldsymbol{q}}} \right)\tau ^x + t_{pp}{\mathrm{Im}}\left( {h_{\boldsymbol{q}}} \right)\tau ^y{,}$$

(18)

with $h_{\boldsymbol{q}} = 1 - e^{iq_x} - e^{ - iq_y} + e^{i\left( {q_x - q_y} \right)}$. Here, we suppress the second-order terms of the strong-coupling expansion, which simply renormalize the dispersion. If one considers the motion of O holes in the background of AF ordered Cu spins, as we have done to calculate the results of Fig. 2a, the dispersion entering $G_0^{ - 1}$ is modified accordingly²⁴ (for details, see the Supplementary Information). The other terms in the Green’s function read

$$\left[ {G_{\mathrm{\Phi }}^{ - 1} + G_{J^\prime }^{ - 1}} \right]\left( {Q,Q^\prime } \right) = A_0\left( {q - q^\prime } \right)\tau ^0 + A_z\left( {q - q^\prime } \right)\tau ^z.$$

(19)

Here, τ⁰ ≡ 1 and we have defined the two functions

$$A_0\left( {q - q^\prime } \right) = \psi _{q - q^\prime } - \mathop {\sum}\limits_{\boldsymbol{p}} {\kern 1pt} {\cal S}_{{\boldsymbol{p}},{\boldsymbol{q}} - {\boldsymbol{q}}^\prime }h_n\left( {{\boldsymbol{p}},{\boldsymbol{q}}^\prime - {\boldsymbol{q}}} \right){,}$$

(20)

$$A_z\left( {q - q^\prime } \right) = \phi _{q - q^\prime } - \mathop {\sum}\limits_{\boldsymbol{p}} {\kern 1pt} {\cal S}_{{\boldsymbol{p}},{\boldsymbol{q}} - {\boldsymbol{q}}^\prime }h_\eta \left( {{\boldsymbol{p}},{\boldsymbol{q}}^\prime - {\boldsymbol{q}}} \right){,}$$

(21)

with Cu spin bilinear ${\cal S}_{{\boldsymbol{p}},{\boldsymbol{q}}} = {\boldsymbol{S}}_{\boldsymbol{p}} \cdot {\boldsymbol{S}}_{ - {\boldsymbol{p}} - {\boldsymbol{q}}}$ and lattice functions $h_{n/\eta }({\boldsymbol{p}},{\boldsymbol{k}})$ = $\frac{{J^\prime }}{2}\left( {e^{ip_x} \pm e^{ip_y} + e^{ - i\left( {p_x + k_x} \right)} \pm e^{ - i\left( {p_y + k_y} \right)}} \right)$, where the upper (lower) sign relates to h_n (h_η).

Integrating over the O degrees of freedom results in an action of the form

$$S = {\int}_q {\kern 1pt} {\mathrm{\Phi }}_q^\dagger U_q{\mathrm{\Phi }}_q - {\mathrm{Tr}}\,{\mathrm{ln}}\left( { - G^{ - 1}} \right),$$

(22)

We expand this expression to second order $S_2 = \frac{1}{2}{\mathrm{Tr}}\left[ {\left\{ {G_0\left( {G_{\mathrm{\Phi }}^{ - 1} + G_{J^\prime }^{ - 1}} \right)} \right\}^2} \right]$ in order to find

$$S_2 = - \frac{1}{2}{\int}_q {\kern 1pt} \mathop {\sum}\limits_{\alpha ,\alpha ^\prime } {\kern 1pt} A_\alpha (q)A_{\alpha ^\prime }( - q){\mathrm{{\Pi}}}_{ - q}^{\alpha \alpha ^\prime },$$

(23)

which includes the biquadratic exchange K term. Here, we have introduced the oxygen density response function

$${\mathrm{{\Pi}}}_q^{\alpha \alpha ^\prime } = - {\int}_k {\kern 1pt} {\mathrm{Tr}}\left[ {G_0(k)\tau ^\alpha G_0(k + q)\tau ^{\alpha ^\prime }} \right]{\kern 1pt} .$$

(24)

The bare biquadratic exchange constant K₀ is given by the zz-component of this response function at zero frequency as

$$K_0 = \frac{{(J^\prime)^2}}{2}{\int}_{\boldsymbol{q}} {\kern 1pt} {\mathrm{{\Pi}}}_{\boldsymbol{q}}^{zz}.$$

(25)

Note that we write ${\mathrm{{\Pi}}}_{\boldsymbol{q}}^{zz} \equiv {\mathrm{{\Pi}}}_{\boldsymbol{q}}^\eta$ in the main text. It is straightforward to obtain the biquadratic exchange renormalized by O density fluctuations by performing the Gaussian integration over the HS fields in Eq. (22), which yields the renormalized response function

$${\tilde{\mathrm {\Pi}}}_{\boldsymbol{q}}^{\alpha \alpha ^\prime } = {\mathrm{{\Pi}}}_{\boldsymbol{q}}^{\alpha \alpha ^\prime } + \frac{1}{2}\mathop {\sum}\limits_{\beta ,\beta ^\prime } \left( {\tilde U_{\boldsymbol{q}}^{ - 1}} \right)_{\beta \beta ^\prime }{\mathrm{{\Pi}}}_{\boldsymbol{q}}^{\beta \alpha }{\mathrm{{\Pi}}}_{\boldsymbol{q}}^{\beta ^\prime \alpha ^\prime }{,}$$

(26)

where we have defined $\left( {\tilde U_q} \right) = \left( {U_{\boldsymbol{q}}} \right)_{\alpha \alpha ^\prime } - \frac{1}{2}{\mathrm{{\Pi}}}_q^{\alpha \alpha ^\prime }$. Approximating the local response by the long-wavelength q = 0 component ${\tilde{\mathrm {\Pi}}}_{ii}^{zz} \approx {\tilde{\mathrm {\Pi}}}_{{\boldsymbol{q}} = 0}^{zz}$ yields the renormalized biquadratic exchange constant K as given in Eq. (4) of the main text.

Nematic susceptibility within soft-spin quantum field theory

In the main text, we analyze the nematic susceptibility χ_nem in the t–J–K-model using a soft-spin quantum field theory. This allows us to investigate the effect of quantum fluctutations on the nematic response. Our main results are shown in Fig. 3. After decoupling the biquadratic K term using HS variable φ_r the soft-spin action reads

$$\begin{array}{*{20}{l}} S \hfill & = \hfill & {\gamma {\int}_q \left[ {r_0 + q^2 + \left( {\varphi _r + h_\varphi } \right)\left( {q_x^2 - q_y^2} \right) + \gamma \left| {\omega _n} \right|^{\frac{2}{z}}} \right]M_q^\alpha M_{ - q}^\alpha } \hfill \\ {} \hfill & {} \hfill & { \,+\, \frac{{\gamma ^2u}}{{2N}}{\int}_{q_1,q_2,q_3} {\kern 1pt} M_{q_1}^\alpha M_{q_2}^\alpha M_{q_3}^\beta M_{ - q_1 - q_2 - q_3}^\beta + {\int}_r \frac{{N\varphi _r}}{{2g}}.} \hfill \end{array}$$

(27)

Here, M_q denotes an N-component Néel magnetization order parameter (N = 3 in the physical system) and summation over repeated indices α, β is implied. The integrations are over ${\int}_r = {\int}_0^{1/T} {\kern 1pt} d\tau {\int} {\kern 1pt} d^2r$ and ${\int}_q = T\mathop {\sum}\nolimits_{\omega _n}^{{\mathrm{\Lambda }}_\omega } {\kern 1pt} {\int} \frac{{d^2{\boldsymbol{q}}}}{{(2\pi )^2}}$ up to some dimensionless momentum and frequency cutoffs Λ and _γΛ_ω. The parameter r₀ controls the distance to the quantum-critical point separating a Néel ordered regime from a quantum disordered paramagnetic regime, u is an interaction constant and the coupling constant g ∝ K/J is proportional to the biquadratic exchange. We have added a source field h_φ ≡ h_r that couples to homogeneous nematic order. We use a dynamic critical exponent of z = 2 in the following, which describes damping due to particle-hole excitations in the presence of mobile holes.

The nematic susceptibility in Eq. (7) can be calculated from the partition function $Z = {\int} {\cal D}\left( {{\boldsymbol{M}}_q,\varphi _r} \right)e^{ - S}$ as

$$\chi _{{\mathrm{nem}}} = \frac{T}{{L^2}}\left. {\frac{{\partial ^2Z}}{{\partial h_\varphi ^2}}} \right|_{h_\varphi = 0} = \frac{{\chi _{{\mathrm{nem}},0}}}{{1 - \frac{g}{N}\chi _{{\mathrm{nem}},0}}}$$

(28)

where L is the linear system size and the bare nematic susceptibility is given by

$$\chi _{{\mathrm{nem}},0} = \frac{N}{g} - \frac{T}{{L^2\left\langle {\bar \varphi _r^2} \right\rangle }}{\kern 1pt} ,$$

(29)

with $\bar \varphi _r = \varphi _r + h_\varphi$. In the following, we consider homogeneous HS fields φ_r, $\bar \varphi _r$. To calculate the expectation value $\left\langle {\bar \varphi _r^2} \right\rangle$, we first decouple the quartic u-term in Eq. (27) using HS field ψ, then separate longitudinal and transverse components ${\boldsymbol{M}}_r = \left( {\sqrt N M,{\boldsymbol{\pi }}_r} \right)$ and integrate over the transverse ones to arrive at the (dimensionless) action s ≡ S/[L²(γT)⁻¹] given by

$$\begin{array}{*{20}{l}} s \hfill & = \hfill & {NrM^2 + \frac{{N\left( {\bar \varphi _r - h_\varphi } \right)^2}}{{2\tilde g}} - \frac{{\psi ^2}}{{2\tilde u}}} \hfill \\ {} \hfill & {} \hfill & { + \frac{{N - 1}}{2}\gamma {\int}_q {\kern 1pt} {\mathrm{ln}}\left( {r_q + \bar \varphi _r\left( {q_x^2 - q_y^2} \right)} \right){\kern 1pt} } \hfill \end{array}{.}$$

(30)

Here, r_q = r + q² + γ|ω_n|, r = r₀ + ψ and we have defined dimensionless interaction constants $\tilde g = g{\mathrm{/}}\gamma$ and $\tilde u = u{\mathrm{/}}\gamma$. Next, we expand the logarithm in small $\bar \varphi _r$ up to second order and obtain Eq. (29) by differentiation as

$$\chi _{{\mathrm{nem}},0} = \frac{{NT}}{2}\mathop {\sum}\limits_{\omega _n} {\int} ^{\mathrm{\Lambda }}\frac{{d^2q}}{{(2\pi )^2}}\frac{{q^4{\mathrm{cos}}^2(2\theta )}}{{\left( {r + q^2 + \gamma \left| {\omega _n} \right|} \right)^2}}.$$

(31)

We can exactly perform the summation over Matsubara frequencies (without imposing a frequency cutoff), the momentum integration and then absorb the cutoff Λ by expressing χ_nem,0 in terms of the dimensionless variables $\tilde T = \gamma T{\mathrm{/\Lambda }}^2$ and $\tilde r = r{\mathrm{/\Lambda }}^2$. The lengthy expression is given in the Supplementary Information together with a three-dimensional plot as a function of $\tilde T$ and $\tilde r$. Cuts for different functional behaviors of the magnetic Néel correlation length on temperature r(T) ≡ ξ⁻²(T) are shown in Fig. 3a.

We can derive the functional behavior of r(T) within a large-N approach, where we need to solve the following well-known self-consistency equation

$$r = r_0 + uM^2 + \frac{u}{2}{\int}_q \frac{1}{{r + q^2 + \gamma \left| {\omega _n} \right|}}.$$

(32)

Solving this equation requires us to introduce a finite frequency cutoff Λ_ω, but the qualitative behavior of χ_nem,0 and χ_nem does not depend on the cutoff choice as long as ${\mathrm{\Lambda }},{\mathrm{\Lambda }}_\omega \gg r,\gamma T$. The results for χ_nem,0 and χ_nem shown in Fig. 3b, c are obtained from the large-N solution of r(T) for fixed parameters $\tilde u,{\mathrm{\Lambda }},{\mathrm{\Lambda }}_\omega$ and distance to the quantum-critical point δr₀ = r − r_0,c.

Details on the classical Monte-Carlo simulations

The Monte-Carlo simulations were carried out at 100 equally spaced temperature points in the interval 0.001 < T/J < 2.971. We applied a combination of single-move Metropolis Monte-Carlo steps and nonlocal parallel-tempering-exchange steps between neighboring temperature configurations. The simulations shown in Fig. 2b, c of the main text were carried out for systems of 40 × 40 spins and biquadratic exchange couplings K/J = {0.0, 0, 35, 0.45}. We consider a ferromagnetic next-nearest-neighbor exchange coupling J₂ = −0.1J as well. Note that the ground state phase transition in the classical model between Néel and collinear order occurs at J/2 = J₂ + K. Following thermalization, the averages were computed for each temperature with at least 4.5 × 10⁶ Monte-Carlo sweeps (MCS). The error bars were estimated by using the well-known Jackknife procedure.

Finally, we mention that we have performed Monte-Carlo simulations also for the purely bilinear spin Hamiltonian that is obtained from H_J–K by using the well-known relations valid for spin-1/2 operators: $\left( {{\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_j} \right)^2 = \frac{3}{{16}} - \frac{1}{2}{\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_j$ and $\left( {{\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_j} \right)\left( {{\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_k} \right) = \frac{1}{4}{\boldsymbol{S}}_j \cdot {\boldsymbol{S}}_k + \frac{i}{2}{\boldsymbol{S}}_i \cdot \left( {{\boldsymbol{S}}_j \times {\boldsymbol{S}}_k} \right)$. These allow rewriting the biquadratic K term as a sum of three bilinear spin exchange terms

$$\begin{array}{*{20}{l}} {\tilde H_{J - K}} \hfill & = \hfill & {\frac{1}{2}\left( {J + \frac{K}{{4S^2}}} \right)\mathop {\sum}\limits_i \mathop {\sum}\limits_\delta {\kern 1pt} {\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_{i + \delta }} \hfill \\ {} \hfill & {} \hfill & { \,+\, \frac{K}{{8S^2}}\mathop {\sum}\limits_i \mathop {\sum}\limits_{\delta \prime } {\kern 1pt} {\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_{i + \delta^{\prime} } - \frac{K}{{16S^2}}\mathop {\sum}\limits_i \mathop {\sum}\limits_{\delta ^{\prime \prime} } {\kern 1pt} {\boldsymbol{S}}_i \cdot {\boldsymbol{S}}_{i + \delta ^{\prime \prime} }{\kern 1pt} } \hfill \end{array}{.}$$

(33)

Here, δ(δ′) runs over the (next-)nearest neighbors of the square lattice and δ″ runs over the second-neighbors along the bonds. Importantly, classical Monte-Carlo simulation results for this Hamiltonian $\tilde H_{J - K}$ show the same enhancement of the nematic susceptibility χ_nem as a function of K as results for the original Hamiltonian H_J−K that includes the biquadratic exchange term.