Abstract
Weyl semimetal defines a material with three-dimensional Dirac cones, which appear in pair due to the breaking of spatial inversion or time reversal symmetry. Superconductivity is the state of quantum condensation of paired electrons. Turning a Weyl semimetal into superconducting state is very important in having some unprecedented discoveries. In this work, by doing resistive measurements on a recently recognized Weyl semimetal TaP under pressures up to about 100 GPa, we show the concurrence of superconductivity and a structure transition at about 70 GPa. It is found that the superconductivity becomes more pronounced when decreasing pressure and retains when the pressure is completely released. High-pressure x-ray diffraction measurements also confirm the structure phase transition from I41 md to P-6m2 at about 70 GPa. More importantly, ab-initial calculations reveal that the P-6m2 phase is a new Weyl semimetal phase and has only one set of Weyl points at the same energy level. Our discovery of superconductivity in TaP by high pressure will stimulate investigations on superconductivity and Majorana fermions in Weyl semimetals.
Similar content being viewed by others
Introduction
Superconductivity and topological quantum state are two important fields of frontier research in nowadays condensed matter physics.1,2,3 Superconductivity is the state of quantum condensation of paired electrons. A Weyl semimetal defines a kind of materials with three-dimensional Dirac cones, which appear in pair with opposite spin chirality due to the breaking of spatial inversion or time reversal symmetry. The relevant electronic bands of a Weyl semimetal may cross or pass through nearby the so-called Weyl nodes with different chirality and the low-energy excitations near these points disperse linearly in the momentum space. It naturally contains the long sought novel quasiparticle excitations, namely the Weyl fermions.4,5 When the Weyl semimetal falls into superconducting state, it is possible to observe some exotic excitations, such as the Majorana fermions.6,7 Therefore, turning a Weyl semimetal into superconducting state is very important in having some unprecedented discoveries.
Recently, TaAs and TaP were predicted to be Weyl semimetals,8,9 which is followed immediately by experimental proofs.10,11,12,13,14 The Weyl semimetal normally exhibits a giant and sometime negative magnetoresistance (MR) due to the semimetal behavior and the opposite spin chirality of the paired Weyl nodes.15,16,17,18 It is very interesting and highly desired to realize bulk superconductivity in such Weyl semimetals.19 Previously, Wang et al. observed superconducting-like anomaly in the point contact tunneling spectrum on TaAs.20 The recent measurements under high pressure on Weyl semimetals NbAs and TaAs have revealed some interesting physics,21,22 but did not show the trace of superconductivity. While transition metal dichalcogenides materials, MoTe2 and WTe2, were found to show superconductivity under high pressure and both of them were considered to be the type-II Weyl semimetal.19,23,24,25,26,27,28,29,30,31,32,33,34,35 In this paper, we report, for the first time, the discovery of bulk superconductivity accompanied by a structure phase transition in Weyl semimetal TaP by applying high pressure. More importantly, first-principles calculations confirm that the P-6m2 phase with superconductivity induced by high pressure has the Weyl semimetal feature, but is distinct from the ambient phase.
Results
Resistivity and MR under different pressures
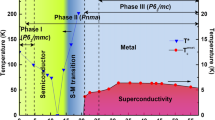
In Fig. 1, we show the temperature-dependent resistance R(T) of a TaP single crystal under different pressures up to 92 GPa. The pristine sample is a TaP single crystal with high quality, as characterized by x-ray diffraction (XRD), residual resistivity ratio (RRR≈31), and giant MR (about 30,000% at 8 T) with clear quantum oscillations. The large value of RRR implies low density of impurities or disorders in the sample at ambient pressure. The related data are presented in Supplementary Figs. 1 and 2, and Supplementary Note 3. Figure 1a, b display the raw data of resistance under pressures from 0.4 to 14.6 GPa (referred as low-pressure region) and from 19.2 to 92 GPa (high-pressure region), respectively. The resistivity measurements under high pressure are given in section “Methods” and Supplementary Note 4. The resistance globally gets enhanced with applied pressure starting from ambient pressure, and reaches a maximum value at about 19.2 GPa. Then the resistance decreases monotonically as the pressure continues to increase. Three-dimensional contour plot of resistance with temperature and pressure is shown in Fig. 1c. The ridge like surface graphically shows the variation of resistance with temperature and pressure. Six typical R(T) curves with pressures of 0.4, 5.0, 8.5, 19.2, 46.3 and 80.0 GPa are representatively highlighted in the contour plot. We will see later that this complex evolution of resistivity is closely related to the crossing of Fermi energy through the paired Weyl points.
Temperature-dependent resistance under pressures. a Temperature dependence of resistance for pressures from 0.4 to 14.6 GPa, and those from 19.2 to 92.0 GPa are shown in b. The inset of b shows the magnetoresistance at 4.5 K up to 8 T under different pressures. c The three-dimensional contour plot of resistance vs. temperature under different pressures
Figure 2a shows the change of resistance at 5 and 300 K under different pressures. Figure 2b presents the MR at different pressures. One can see that now the MR at 0.4 GPa and 8 T is about 275%, which is much smaller than that measured on the pristine sample at ambient pressure. This may be induced by two reasons: (1) the direction of applied magnetic field is different from the one in the case of measurement at ambient pressure; (2) the non-uniform stress under a pressure. We calculated electronic resistance of the I41 md structure and the DOS near Fermi level using DFT and the semi-classic Boltzmann transport theory, as shown in Fig. 2d. In TaP or TaAs families, the Weyl points can be divided into two types according to their positions in reciprocal space: W1 (k z = 0) and W2 (k z ≠ 0), these two types of Weyl points locate at different energies.8,9 At ambient pressure, the energy of W1 is 50 meV under the Fermi level and that of W2 is about 15 meV above Fermi level, as shown in Fig. 2e. We focus on the energy of W2 at different pressures, which may have more significant influence on the density of states near the Fermi level and thus the electrical conductivity than W1. The energy of W2 relative to Fermi level changes significantly with pressure by our calculations. The detailed calculation results are given in Supplementary Note 1 and Supplementary Table 1. W2 is above the Fermi level at low pressures, and becomes below the Fermi level when a pressure at around 20 GPa is applied. Thus, when the pressure is increased to about 20 GPa, the finite DOS corresponding to this Weyl point is getting smaller, leading to the increase of the global resistivity. When the pressure is larger than about 20 GPa, the reversal process dominates. The W2 point becomes below the Fermi energy and the DOS becomes larger leading to the dropping down of the global resistance. This picture also gets support from the behavior of MR measurement. A giant MR shows up at a low pressure, which was considered as a result of the contribution of the electron and hole pockets in the material. More in detail, from the semi-classical two-band model, the MR can be calculated as follows:
where \(\rho _0\) is the resistivity at zero field, \(\sigma _i = n_ie^2\tau _i/m_i\)(i = h, e) is the conductivity (being always positive) at the hole and electron derived band, respectively. And \(\mu _i = e_i\tau _i/m_i\)(i = h,e) is the mobility of each band with a negative (positive) sign for the electron (hole) band. At ambient pressure, the Fermi energy is in between W1 and W2 (close to W2), we have an electron and hole contribution for conductivity from the Weyl nodes of W1 and W2, respectively, therefore we have a sizable MR. With compression, the chemical potential gets higher and becomes closer to W2. The electron-pocket Fermi surfaces around W1 become larger while the hole-pocket Fermi surfaces around W2 become smaller. Therefore, it is natural that the MR decreases when increasing pressure. Superconductivity has been induced in some materials with giant MR23,24,36,37,38 when pressure is applied. In the following, we will show that superconducting behavior has also been detected in TaP with further increasing pressure.
Resistance and MR under pressure. a Resistance at 5 and 300 K vs. pressure. Both of them show a maximum value at about 19.2 GPa. Four insets in a indicate the change of Fermi level relative to W2 from 0 to 30 GPa through band structure calculations. The Fermi level crosses the Weyl points between 10 and 20 GPa, which corresponds to the maximum value of resistance at pressures around 20 GPa. b, c show the MR vs. magnetic field and pressure, respectively. d, The calculated semi-classic transport resistance (black squares) and the DOS near Fermi level (red circles) of the I41 md phase vs. pressure. e Energies of W2 relative to the Fermi level under different pressures and local band structures of two kinds of Weyl points in the I41 md phase. The Dirac cones are schematically shown together with the Fermi level (grey disc) under different pressures. The red line shows the energy of W2 evolution along with pressure. Weyl points are denoted by red and green dots to represent opposite chirality
Superconductivity induced by high pressure
When the applied pressure reaches 71.0 GPa, the resistance shows a small drop at about 2.3 K, this is shown in Fig. 3a and amplified in the lower-right inset in the low-temperature region. This drop becomes more pronounced with pressure up to 100 GPa. In order to check whether this drop corresponds to a superconducting transition, we measure the temperature dependence of resistance under different magnetic fields. The upper-left inset reveals the resistive transitions at different external magnetic fields up to 1 T at 92 GPa. It is clear that the transition is gradually suppressed by external magnetic field, which is a typical behavior of a superconductor. Unfortunately, our high-pressure resistive measurement setup cannot be cooled below 1.7 K, therefore we cannot reach the state with zero resistance. Meanwhile, the maximum pressure of the experimental setup is about 100 GPa, so we cannot further increase the pressure on the sample. We emphasize that the control experiment has been done on another sample and the occurrence of superconductivity at about 70 GPa and above is proved. Interestingly, when we decrease the pressure this resistance transition becomes much more pronounced. The data measured in the pressure decreasing procedure is shown in Fig. 3b. The resistance drop has a magnitude of about 75% of the normal state value ρ n at 30 GPa, while it reduces with further lowering pressure, as shown in the left inset of Fig. 3b. In the decompression process of control experiment, a sharp superconducting transition was observed at about 80.1 GPa. And the superconducting transition remains until releasing pressure to 23.7 GPa, then the experiment was interrupted. These experiments rule out any possibility that the superconductivity arises from the possible impurity phase of Ta, since Ta is superconductive at about 4.48 K at ambient pressure. In addition, because there are no magnetic atoms in TaP, this transition with a drop of about 75% ρ n cannot be ascribed to any magnetic transitions. The sharp drop of resistance and the magnetic field dependence demonstrate that this transition is a superconducting transition. Judged from the sharpness of the transition, we conclude that bulk superconductivity has already been induced, although it is still not completely uniform owing to the non-uniformity of high pressure. As mentioned above, due to the lower limit temperature of our instrument, we could not detect the zero resistance state. But one can see that the zero resistance temperature is certainly expectable, which is suggested by the 75% dropping of resistivity within a temperature window of only 1.37 K (from about 1.7 to 3.07 K) and the resistivity does not exhibit a flattening in the low-temperature region. This excludes the possibility that the superconductivity is filamentary like. The inset on the right-hand side of Fig. 3b shows the correlation of T c vs. pressure. The onset T c (98% of ρ n) decreases from about 3.07 K at 30 GPa to about 1.84 K at 2 GPa when we reduce the pressure. The fact that superconductivity retains after pressure released may suggest that TaP transforms to a metastable phase, which shows superconductivity under a high pressure and it keeps to ambient pressure.
Temperature-dependent resistance with increasing and decreasing pressures. a Temperature-dependent resistance from 92 to 100 GPa with increasing pressure. The R(T) curves under different pressures with decreasing pressure are shown in b. The upper-left inset in a shows the resistance vs. temperature under different fields at 92 GPa, and the lower-right inset shows the enlarged view of the data measured near 71 GPa in low-temperature region. The superconductivity is further evident by a sharp 75% drop of the normal state resistance under 30 GPa, as shown in the left inset in b. The inset on the right-hand side in b shows the pressure dependence of T c in decreasing pressure
Since superconductivity survives when the pressure is released, we thus did a new round of pressurizing experiment and then measure resistivity at ambient pressure. We chose a new TaP sample and ramp the pressure up to 100 GPa, keep it for 24 h (in order to have a uniform phase under high pressure) at room temperature and then release the pressure to ambient. Afterwards, we measure the resistivity down to 0.3 K, and we successfully confirm the superconducting transition. Since the sample is too small with an irregular shape after exfoliated from the high-pressure cell, we can only make two electric contacts on the sample. The residual resistance here is due to the contacting resistance. Moreover, since the sample is too small, with a full volume of superconductivity and under an external magnetic field of 10 Oe, the total magnetization is only about 10−7 emu, which is just at the marginal of measurement sensitivity. The readers are referred to Supplementary Note 2 and Supplementary Fig. 3 for details. In addition, the transitions under different magnetic fields are also determined yielding the upper critical field µ 0 H c2(T) at the pressure released state.
XRD under high pressure
In order to understand the pressure-induced superconductivity in TaP single crystals, we further perform High-pressure-XRD (HP-XRD) experiments up to 101.66 GPa, as detailed in Supplementary Note 5. The HP-XRD results are shown in Fig. 4a. The diffraction peaks gradually move to higher angles indicating that the lattice parameters become smaller. The data are also collected when the sample is decompressed to ambient pressure, as shown in the top of Fig. 4a. It seems that the data at 101.66 GPa have almost the same diffraction pattern with that after the pressure is released to ambient one, the only difference is that the peaks globally shift due to the external pressure. Upon increasing pressure, some peaks, for example those indexed by (103) and (105) become weakened and gradually vanish above about 53.94 and 71.08 GPa, respectively. However, some other peaks show a systematic shift and weaken, but which do not disappear, for example (004) and (020). These evolutions are indicated by red dashed lines in Fig. 4a. Figure 4b shows the intensity evolution of these four peaks mentioned above. Shown in Fig. 4c is the emergence of the peak (021) at 71.08 GPa and beyond, which is indexed to the P-6m2 structure. These results give the evidence that there is indeed a structure phase transition around 70 GPa. This pressure is consistent with the one for the emergence of superconductivity, so we believe that the superconductivity is closely related to the structure P-6m2 of TaP. By using the high-pressure structure P-6m2, which is illustrated on the right-hand side of Fig. 4d, the XRD data with pressure released can be fitted very well, as shown in Fig. 4e. Interestingly, in ref. 22 the authors also find that TaAs transforms to P-6m2 structure at 14 GPa and the structure can be reserved to ambient pressure. This stabilization of high-pressure phase in TaP is exactly the same as TaAs, but in TaAs no superconductivity was discovered above 1.8 K with the structure of P-6m2. We must mention that the data at 101.66 GPa can still be fitted with this structure, with some peaks broadened and deviated a little bit. This deviation may be due to the pressure inhomogeneity within the sample as the applied pressure is rather high. Due to the almost coincident pressure for both the emergence of superconductivity and the new structure P-6m2 at about 70 GPa, we thus can naturally conclude that superconductivity arises from TaP with the P-6m2 structure.
HP-XRD results and the high-pressure structure of TaP. a The high-pressure x-ray diffraction of TaP up to 101.66 GPa. The red dashed lines highlight the evolution of some selected peaks. b Relative diffraction intensity of four selected peaks normalized by that of the (112) peak vs. applied pressures. c The emergence of (021) peak belonging to the P-6m2 structure when the pressure exceeds 71.08 GPa (green line), which clearly indicates the structure phase transition. d Crystal structures of I41 md and P-6m2 phases (elaborated using the VESTA software39). TaP adopts I41 md space group at ambient pressure and transforms to P-6m2 at about 70 GPa. This high-pressure phase can be reserved after external pressure released. e XRD data after decompressing (symbols) and the fitting result using the P-6m2 structure (black solid line)
Discussion
Next we study the electronic structures and surface states of this new P-6m2 TaP. The ab initial calculations are detailed in section “Method” and Supplementary Note 6. Our calculations show that TaP P-6m2 phase is a new topological Weyl semimetal, similar to TaAs high-pressure phase22 P-6m2. The band structures around the Weyl point of the P-6m2 phase at 70 GPa are shown in Fig. 5a, which exhibits linear energy dispersion near the Weyl point. According to our calculation, there are six pairs of Weyl points near the K point, as shown in Fig. 5b. All the Weyl points can be related to each other by mirror and C 3 rotation symmetry, so that there is only one set of Weyl points in this system and they are at the same energy. The surface state of P termination (100) surface are calculated based on the Wannier orbitals and surface Green’s functions.40 There are two kinds of projected Weyl points in Fig. 5c, WD (two Weyl points of same chirality projected to the same position) and WS (single Weyl point projected). Figure 5d, e show that detail surface states near WS and WD. As for WD, there are two Fermi arcs connected to this projected point. For WS, there is only one Fermi arc connected WS and another WS across the first Brillouin zone boundary. These interesting theoretical results indicate clearly that the TaP P-6m2 phase has still the Weyl semimetal feature, which is quite different to the ambient I41 md phase.
Electronic structures and surface states of the TaP P-6m2 phase at 70 GPa. a The band structures around the Weyl point along the path parallel with Γ–K high-symmetry line. b The bulk Brillouin zone and its projection on (100) direction. The Weyl points with opposite chirality are marked by red and yellow, respectively. c–e The Fermi surface of TaP (100)-surface states of P atom termination. And the chemical potential is set at energy of Weyl point. WS and WD mark the projection points of single Weyl point and two Weyl points of same chirality, respectively
Superconductivity is discovered by resistivity measurement in TaP when the pressure exceeds about 70 GPa. HP-XRD also reveals a structure phase transition from I41 md to P-6m2 at a similar pressure, which is related to the emergence of superconductivity. This high-pressure phase and superconductivity can be retained when the pressure is released. It would be interesting to know what leads to the superconductivity and which band plays the dominant role of Cooper pairing. Ab initial calculations on TaP with the high pressure converted P-6m2 structure indicate that it is a new Weyl semimetal with the typical surface Fermi arc state. Unfortunately, angle resolved photo-emission spectroscopy (ARPES) cannot be done under pressure for this state in order to check the surface Fermi arc. It is widely expected that the order parameter of superconductivity by electrons with the spin chirality due to the Weyl semimetal feature should have complex compositions, for example, some component with triplet pairing is inevitable. Thus, it is highly desired to investigate the superconducting gap structure of this novel superconducting phase. Superconductivity discovered directly from pressurized Weyl semimetal TaP will stimulate further efforts in investigating superconductivity in topological materials and paving a possible path to the ultimate discovery of topological superconductors.
Methods
TaP single crystals were synthesized by chemical vapor transport method.16 The sample at ambient pressure has high quality with a nice fitting to the x-ray XRD pattern and clear exhibition of large MR. High-pressure resistance measurements with repeating cycles were conducted via the four-probe method in a screw pressure-type diamond anvil cell. HP-XRD measurements were carried out with angle-dispersive diffraction mode at the beamline 16BM-D, High-Pressure Collaborative Access Team (HPCAT), Advanced Photon Source, Argonne National Laboratory.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Qi, X. L. & Zhang, S. C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Sato, M. & Ando, Y. Topological superconductors: a review. Rep. Prog. Phys. 80, 076501 (2017).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4. Phys. Rev. Lett. 107, 186806 (2011).
Sau, J. D. & Tewari, S. Topologically protected surface Majorana arcs and bulk Weyl fermions in ferromagnetic superconductors. Phys. Rev. B 86, 104509 (2012).
Chen, A. & Franz, M. Superconducting proximity effect and Majorana flat bands at the surface of a Weyl semimetal. Phys. Rev. B 93, 201105(R) (2016).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Huang, S. M. et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Xu, S. Y. et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 1, e1501092 (2015).
Xu, N. et al. Observation of Weyl nodes and Fermi arcs in tantalum phosphide. Nat. Commun. 7, 11006 (2016).
Inoue, H. et al. Quasiparticle interference of the Fermi arcs and surface-bulk connectivity of a Weyl semimetal. Science 351, 1184–1187 (2016).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Arnold, F. et al. Negative magnetoresistance without well-defined chirality in the Weyl semimetal TaP. Nat. Commun. 7, 11615 (2016).
Du, J. et al. Unsaturated both large positive and negative magnetoresistance in Weyl Semimetal TaP. Sci. China—Phys. Mech. Astron. 59, 657406 (2016).
Huang, X. C. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Zhang, C. L. et al. Large magnetoresistance over an extended temperature regime in monophosphides of tantalum and niobium. Phys. Rev. B 92, 041203 (2015).
Qi, Y. P. et al. Superconductivity in Weyl semimetal candidate MoTe2. Nat. Commun. 7, 11038 (2016).
Wang, H. et al. Discovery of tip induced unconventional superconductivity on Weyl semimetal. Sci. Bull. 62, 425–430 (2017).
Zhang, J. et al. Structural and transport properties of the Weyl semimetal NbAs at high pressure. Chin. Phys. Lett. 32, 097102 (2015).
Zhou, Y. et al. Pressure-Induced New Topological Weyl Semimetal Phase in TaAs. Phys. Rev. Lett. 117, 146402 (2016).
Pan, X. C. et al. Pressure-driven dome-shaped superconductivity and electronic structural evolution in tungsten ditelluride. Nat. Commun. 6, 7805 (2015).
Kang, D. et al. Superconductivity emerging from a suppressed large magnetoresistant state in tungsten ditelluride. Nat. Commun. 6, 7804 (2015).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Wu, Y. et al. Observation of Fermi arcs in the type-II Weyl semimetal candidate WTe2. Phys. Rev. B 94, 121113(R) (2016).
Wang, C. L. et al. Observation of Fermi arc and its connection with bulk states in the candidate type-II Weyl semimetal WTe2. Phys. Rev. B 94, 241119(R) (2016).
Bruno, F. Y. et al. Observation of large topologically trivial Fermi arcs in the candidate type-II Weyl semimetal WTe2. Phys. Rev. B 94, 121112(R) (2016).
Wang, Z. J. et al. MoTe2: a type-II Weyl topological metal. Phys. Rev. Lett. 117, 056805 (2016).
Sun, Y., Wu, S. C., Ali, M. N., Felser, C. & Yan, B. Prediction of Weyl semimetal in orthorhombic MoTe2. Phys. Rev. B 92, 161107(R) (2015).
Huang, L. et al. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe2. Nat. Mater. 15, 1155–1160 (2016).
Deng, K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 12, 1105–1110 (2016).
Jiang, J. et al. Signature of type-II Weyl semimetal phase in MoTe2. Nat. Commun. 8, 13973 (2017).
Tamai, A. et al. Fermi arcs and their topological character in the candidate type-II Weyl semimetal MoTe2. Phys. Rev. X 6, 031021 (2016).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205–208 (2014).
Zhou, Y. et al. Pressure-induced superconductivity in a three-dimensional topological material ZrTe5. PNAS 113, 2904–2909 (2016).
Qi, Y. P. et al. Pressure-driven superconductivity in the transition-metal pentatelluride HfTe5. Phys. Rev. B 94, 054517 (2016).
Tafti, F. F. et al. Tuning the electronic and the crystalline structure of LaBi by pressure: from extreme magnetoresistance to superconductivity. Phys. Rev. B 95, 014507 (2017).
Momma, K. & Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Wu, Q., Zhang, S., Song, H. F., Troyer, M. & Soluyanov, A. A. Wannier tools: an open-source software package for novel topological materials. Preprint at http://arxiv.org/abs/1703.07789 (2017).
Acknowledgements
We appreciate useful discussions with Yong Chen at Purdue University and Liang Fu at MIT. This work was supported by the Ministry of Science and Technology of China (Grant Nos. 2016YFA0300400, 2015CB921202, and 2016YFA0401804), the National Natural Science Foundation of China (NSFC) with the projects: 11534005, 11190023, 11374143, U1530402, U1532267, 51372112, 11574133, 11574323, U1632275, NSF Jiangsu province (No. BK20150012), the Special Program for Applied Research on Super Computation of the NSFC–Guangdong Joint Fund (the second phase), HPCC of Nanjing University and “Tianhe-2” at NSCC-Guangzhou. The HP-XRD experiments were conducted at HPCAT, which is supported by DOE-NNSA under Award No. DE-NA0001974 and DOE-BES under Award No. DE-FG02-99ER45775, with partial instrumentation funding by NSF. APS is supported by DOE-BES, under Contract No. DE-AC02-06CH11357.
Author information
Authors and Affiliations
Contributions
The samples were grown by Y.F.L. and X.Y.Z. The high-pressure resistivity measurements were conducted by Y.H.Z., X.L.C., X.F.W., C.A., Y.Z., and Z.R.Y. The low temperature with He3 was measured by J.X., Y.F.L., G.D., and H.Y. HP-XRD measurements were done by F.H., W.G.Y., and H.-K.M The structure analysis was done by Y.F.L. and F.H. The DFT calculations were done by Z.P.G., P.C.L., and J.S. H.-H.W. coordinated the whole work. H.-H.W., Y.F.L. and J.S. wrote the manuscript, which is supplemented by others. All authors have discussed the results and the interpretations.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Li, Y., Zhou, Y., Guo, Z. et al. Concurrence of superconductivity and structure transition in Weyl semimetal TaP under pressure. npj Quant Mater 2, 66 (2017). https://doi.org/10.1038/s41535-017-0066-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-017-0066-z
This article is cited by
-
Tunable dual-band dual-polarization terahertz polarization converter and coding metasurfaces based on Weyl semimetals
Applied Physics B (2023)
-
Superconducting ScP4 with a novel phosphorus framework
Applied Physics A (2022)
-
Pressure-induced superconductivity and structure phase transition in Pt2HgSe3
npj Quantum Materials (2021)
-
An ab-initio study on structural, elastic, electronic, bonding, thermal, and optical properties of topological Weyl semimetal TaX (X = P, As)
Scientific Reports (2021)
-
Pressure-induced superconductivity and modification of Fermi surface in type-II Weyl semimetal NbIrTe4
npj Quantum Materials (2021)