An efficient and compact switch for quantum circuits

Abstract

The engineering of quantum devices has reached the stage where we now have small-scale quantum processors containing multiple interacting qubits within them. Simple quantum circuits have been demonstrated and scaling up to larger numbers is underway. However, as the number of qubits in these processors increases, it becomes challenging to implement switchable or tunable coherent coupling among them. The typical approach has been to detune each qubit from others or the quantum bus it connected to, but as the number of qubits increases this becomes problematic to achieve in practice due to frequency crowding issues. Here, we demonstrate that by applying a fast longitudinal control field to the target qubit, we can turn off its couplings to other qubits or buses. This has important implications in superconducting circuits as it means we can keep the qubits at their optimal points, where the coherence properties are greatest, during coupling/decoupling process. Our approach suggests another way to control coupling among qubits and data buses that can be naturally scaled up to large quantum processors.

Introduction

Superconducting quantum circuits^1,2,3,4 are promising candidates to realize quantum processors and simulators. They have been used to demonstrate various quantum algorithms and implement thousands of quantum operations within their coherence time,⁵ in which controllable couplings are inevitable. The typical way to couple/decouple two superconducting quantum elements with always on coupling is to tune their frequencies in or out of resonance,^{6,7,8,9,10,11,12} or with sideband transitions by parametric driven.^13,14 These methods are widely adopted even for the most recent universal gate implementations.^{5,15,16,17,18,19,20,21,22,23,24,25,26} However, they suffer from several issues, namely, it is technically difficult to avoid the frequency crowding problem in large-scale circuits; the qubits cannot always work at the coherent optimal point; and the fast tuning of the qubit frequency results in nonadiabatic information leakage. To overcome the above problems, significant effort both theoretically and experimentally^{27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47} has been devoted to develop coupling methods for parametrically tuning the coupling strength between two quantum components. These proposals or demonstrations either only achieved low fidelity or needs additional circuity to modify the qubit architecture, increasing the complexity of the circuity and bring in additional cross-talk problems, which in the process of scaling up, might be a major hinderance. Therefore, the implementation of a switch for coherent coupling between quantum elements is still a big challenge in scalable quantum circuits.

In this article, we propose and demonstrate a simple architecture-independent method to switch on/off the coupling between two quantum elements via a longitudinal control field.^48–51 We demonstrate this on two different superconducting systems: transmon qubits⁵² of the Xmon variety,⁵³ and flux qubit–resonator systems.⁵⁴ In the first instance (Fig. 1a–c) two qubits Q₁ and Q₂ are coupled through the same coplanar wave guide resonator with coupling strength g₁ ≈ g₂ ≈ 20 MHz, respectively. The qubit frequencies ω₁ and ω₂ are lower than the resonator frequency ω_c = 5.456 GHz with detuning Δ_1,2 = ω_c − ω_1,2. In this dispersive limit, the Hamiltonian of the qubit–qubit system can be written as

$$H_{\mathrm{X}} = \frac{\hbar }{2}\omega _1\sigma _{z,1} + \frac{\hbar }{2}\omega _2\sigma _{z,2} + \hbar g\left( {\sigma _{ + ,1}\sigma _{ - ,2} + \sigma _{ - ,1}\sigma _{ + ,2}} \right),$$

(1)

where g = g₁g₂(Δ₁ + Δ₂)/2Δ₁Δ₂ is the effective coupling strength, and Δ_1,2 = ω_c − ω_1,2 is the detuning of the qubit frequencies from the resonator. Here σ_x, σ_y, and σ_z are the Pauli operators with σ_± = (σ_x ± iσ_y)/2.

Fig. 1

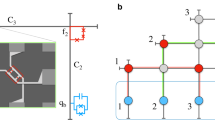
The sample. Optical micrograph and schematic circuit of the qubit–qubit sample and the qubit–resonator sample. In a the two qubits Q₁ and Q₂ (shaded in red) are coupled by a coplanar wave guide resonator (shaded in green). Each qubit consists of a cross-shaped capacitor and a nonlinear inductor from a dc SQUID (shaded in blue). The dc SQUID is formed from shadow-evaporated Al Josephson junctions. A z bias line inductively coupled to the dc SQUID controls the qubit frequency ω₁₍₂₎. The cross-shaped capacitors also serve as ports for capacitively coupling the qubit to the readout resonator, the microwave excitation line (xy), and other qubits. In b, the small area shows the dc SQUID with the the Al Josephson junctions shaded in red, while c is a schematic circuit of the sample with crosses denoting the Josephson junctions. In d for the flux qubit–resonator sample, the coplanar wave guide resonator is marked out by a blue ribbon, while e shows a SEM image of the small structures of the flux qubit circuit. Josephson junctions of the qubit and the readout dc-SQUID are marked out by red and yellow boxes, respectively. A schematic illustration of the gap-tunable flux qubit with control and coupling lines is shown in f. The smaller junction of the three-junction flux qubit is replaced by a dc-SQUID, called the α-loop, in which the flux f_α threading the α-loop is tuned by the current I_α through the α bias line. The α bias line is also used for applying longitudinal control pulses (z pulses) to perform the switch. The qubit is coupled to the resonator through mutual inductance. Qubit flux bias f_ε and microwave pulses are generated by the current I_ε through another microwave line on the left. To achieve high flux bias stability, the flux qubit adopts a gradiometeric geometry. I_r Here i_r denotes the zero-point current of the resonator. The readout dc-SQUID is not shown here

The second system (Fig. 1d–f) can be described by the flux qubit–resonator Hamiltonian as⁵⁵

$$H_{\mathrm{F}} = \frac{\hbar }{2}\left( {{\mathrm{\Delta }}\sigma _{z,1} + \varepsilon \sigma _{x,1}} \right) + \hbar \omega _ra^\dagger a + \hbar g\left( {a^\dagger + a} \right)\sigma _{x,1},$$

(2)

where a^† (a) is the creation (annihilation) operator of the resonator field with the resonance frequency ω_r/2π, and ħΔ is the energy gap of the flux qubit with ħε being the energy difference between the two persistent-current states. The qubit frequency is given by $\omega _1 = \sqrt {{\mathrm{\Delta }}^2 + \varepsilon ^2}$.

Results

Let us focus our attention on our switch for both quantum circuits beginning with the qubit–qubit system.

Qubit–qubit system configuration

We begin by fixing the the qubit frequency of Q₂ at ω₁ = 4.9174 GHz, denoted by the horizontal solid line in Fig. 2a. We then tune the qubit frequency of Q₁ by its z bias line and probe its microwave excitation response. Figure 2a shows the spectroscopic measurement with an anticrossing due to the qubit–qubit coupling clearly observed at 4.9174 GHz. Fitting the spectrum lines (dashed blue curves in Fig. 2a) establishes the coupling strength as g/2π = 0.61 MHz.

Fig. 2

Spectrum of the qubit–qubit and the qubit–resonator systems. In a the spectrum of qubit Q₁ in the qubit–qubit system is displayed. The qubit is driven by a microwave pulse with varied frequency f, which when f matches the qubit frequency ω₁ excites the qubit to its exited state. This increases the excited state occupation probability P. The qubit frequency can then be tuned by a z bias line. With the frequency ω₂/2π of the second qubit Q₂ fixed at 4.9174 GHz (indicated by the horizontal white dashed line) an anticrossing gap Δ_g = 2g/2π = 1.22 MHz of the spectrum lines due to the coupling is clearly visible. Also show as a diagonal white line are the qubit frequencies of Q₁ with zero coupling strength. Further the blue solid curves are fit of the spectrum lines. Next under the longitudinal drive with frequency ω_z/2π = 20 MHz the anticrossing gap Δ_g(λ_z) variation is depicted in b with the amplitude λ_z of the control pulse. Δ_g decreases when increasing λ_z from zero, and reaches an invisible minimum value at the switch-off point λ_z = λ_zoff ≈ 1.2ω_z, indicated by the vertical dashed line. In c the spectrum of the flux qubit Q₁ in the qubit–resonator system is displayed as a function of ε. The qubit is driven by a microwave pulse with variable frequency f, and when f matches the qubit frequency ω_qb the qubit is excited to its exited state. The frequency ω_r/2π of the resonator is 2.417 GHz, indicated by the horizontal white dashed line, while the other white dashed line shows the qubit frequencies at zero coupling strength. The blue dashed curves are fit of the spectrum lines. Clearly shown is an anticrossing due to the coupling with gap Δ_g = 2g/2π = 18.28 MHz. In d the anticrossing gap Δ_g(λ_z) is shown in varying amplitude λ_z of the control pulse with frequency ω_z/2π = 150 MHz at the qubit optimal point. Δ_g decreases when increasing λ_z from zero, and reaches a minimum value at the switch-off point λ_z = λ_zoff ≈ 1.2ω_z indicated by the vertical dashed line, and then reopened again to about 0.4g. The color bars in (a, b) is the occupation probability of the qubit excited state and in (c, d) is the readout signal normalized to the range of [0, 1]

To begin our investigation of switching on/off the qubit–qubit coupling, we apply a control field with frequency ω_z/2π = 20 MHz to Q₁ by the z bias line. This results in a longitudinal interaction Hamiltonian H_L = ħλ_z cos(ω_zt)σ_z,1, where λ_z is determined by the amplitude of the applied rf driving current I_α in the z bias line. By performing an unitary transform U = exp[−i2λ_z sin(ω_zt)σ_z/ω_z], the total Hamiltonian H = H_JC + H_L of the system reduces to the effective Hamiltonian of the form^48,49

$$H_{{\mathrm{eff}}} = \frac{\hbar }{2}\omega _1\sigma _{z,1} + \frac{\hbar }{2}\omega _2\sigma _{z,2} + \hbar g_{{\mathrm{eff}}}\left( {\sigma _{ + ,1}\sigma _{ - ,2} + \sigma _{ - ,1}\sigma _{ + ,2}} \right),$$

(3)

where we have neglected the small fast-oscillating terms assuming $\omega _z \gg g$. In this case g_eff = gJ₀(2λ_z/ω_z) is the effective coupling strength under longitudinal control, where J₀(x) is the zeroth-order Bessel function of the first kind. Our effective Hamiltonian clearly shows that g_eff vanishes when 2λ_z/ω_z is a zero point of the Bessel function J₀(2λ_z/ω_z), that is when λ_z ≈ 1.2ω_z. At this point the qubit–qubit coupling is switched off. Moreover, the coupling strength g_eff can be continuously tuned between two values with opposite signs by changing the ratio 2λ_z/ω_z. We can define the switch on/off ratio R as the ratio between vacuum Rabi frequencies with and without the control field. Henceforth, we will call λ_zoff the switch-off point and a longitudinal control pulse with such an amplitude a switch-off pulse. Here, we have neglected the fast-oscillating terms to give a simplified description to illustrate the idea of this scheme, in methods we have done numerical simulations with the full Hamiltonian (see Methods). In fact, experiment⁵⁶ and theory⁴⁹ have shown that transparency to the transverse classical field can be induced with a longitudinal control pulse. Here, we replace the transverse classical field with a quantum element (qubit or resonator), which becomes decoupled from all transverse interactions. This is the governing principle of our controlled coupling scheme.

For the qubit–qubit case, in view of the qubits small anharmonicities around 250 MHz, we included one extra level in our numerical simulations. Results are consistent with that of the analytical two-level case described by Eq. (3). The driving amplitude used for the qubit-qubit system in this work is well below the qubit anharmonicity and leakage to higher levels is well below 10⁻⁴. Note that if the amplitude approaches the anharmonicity, leakage will become nonnegligible.

Next, to test our longitudinal, control field-based switch we perform spectroscopic measurements on the qubit–resonator system under different amplitudes λ_z of the longitudinal control fields. These are shown in Fig. 2b where it can be seen that the amplitude of the anticrossing gap Δ_g = 2g_eff decreases to zero as λ_z → 1.2ω_z, and then opens up again as λ_z further increases. At the switch-off point λ_zoff ≈ 24 MHz, the amplitude of the anticrossing Δ_g becomes undetectable. This is definite evidence that the coupling can be tuned and switched off by the longitudinal control field.

Qubit–resonator system configuration

Here, we tune the qubit energy gap Δ/2π to be equal to the resonator frequency ω_r/2π = 2.417 GHz by applying a long dc bias in the α bias line (see Fig. 1c). Spectroscopic measurements are then performed. Figure 2c shows the measurement results with an anticrossing due to the qubit–resonator coupling clearly observed at 2.417 GHz. Fitting the spectrum lines (dashed blue curves) allows us to determine the coupling strength as g/2π = 9.14 MHz.

Given we now know g we can now test our switching protocol. Applying a longitudinal control field (similar to the qubit–qubit case) with frequency ω_z and amplitude λ_z, we observed in Fig. 2d that the amplitude of the anticrossing gap Δ_g = 2g_eff decreases to zero as λ_z → 1.2ω_z. The bright spot seen at Δ/2π = 2.417 GHz and near λ_z/2π ~ 180 MHz is the resonator’s resonance signature. When we drive the flux qubit, the resonator can be excited due to coupling with the qubit microwave driving control line. This excitation can be detected because there is coupling between the resonator and the qubit readout SQUID, which results in the bright spot at the resonator frequency in Fig. 2d.

Performance

Our exploration of the switch using spectroscopic measurements has qualitatively shown its operation in both the qubit–qubit and qubit–resonator configurations, yet it is difficult to quantify exactly how well it is operating from those measurements alone. However, time-domain vacuum Rabi oscillation measurements with the switch turned on and off separately will allow us to measure the time scale of the relaxation decay. Figure 3a for the qubit-qubit system and (c) for the qubit–resonator system shows the vacuum Rabi oscillations when the amplitude λ_z of the longitudinal control field is increased from zero. The data clearly shows that the oscillation frequency ω_c = 2g_eff decreases with increasing λ_z. When λ_z reaches the switch-off point λ_zoff, the oscillation frequency reaches a minimum. Further, Fig. 3b for the qubit–qubit system and (d) for the qubit–resonator system shows the comparison of the dynamics without a control pulse (blue) and with switch-off pulse (orange). At the switch-off point the dynamic behavior is an exponential decay—the oscillation frequency is too small to be observed on the experimental data, indicating a very small effective coupling g_eff. The rate of exponential decay due to energy relation in the switched-off state is very close to the decay rate without the switching pulse (shown explicitly in Fig. 3b for the qubit–qubit system). This indicates that the switching pulse does not influence the qubits relaxation time. More quantitatively, the characteristic times for the decays in Fig. 3b are

• 1. Single-qubit energy relaxation rate: T = 15.58 ± 0.28 μs

• 2. No switching pulse with maximal coupling: T = 9.57 ± 0.35 μs

• 3. Switching pulse tuned to turn off the coupling: T = 15.25 ± 0.24 μs

Fig. 3

Switching on/off the coherent oscillation between the qubit–qubit and the qubit–resonator systems. Vacuum Rabi oscillations between the qubit and the resonator under different amplitudes λ_z of longitudinal control pulse for the qubit–qubit a and qubit–resonator c configurations. When λ_z is increased, the oscillation frequency decreases and reaches a minimum at the switch-off point λ_z = λ_zoff, indicated by a red dashed line. The color indicates the occupation probability P of the qubit excited state. This is consistent with the numerical simulation in Fig. 5c. In b for the qubit–qubit and d for qubit–resonator situations we display a comparison between the vacuum Rabi oscillation without (blue) and with (orange) longitudinal control for λ_z = λ_zoff. When the longitudinal control with the amplitude λ_zoff is applied to the qubit, the vacuum Rabi oscillation between the qubit and the resonator vanishes, indicating that the qubit–resonator coupling is switched off. Dots are experimental data, solid curves are both exponential decay fit and exponential decay oscillation fit. As a comparison in the qubit–qubit situation, the qubit decay without switching pulse is also plotted (green dots). Here we observe that the qubit decays at the same rate in both cases. We have also compared $T_2^ \ast$ with and without longitudinal driving and found no noticeable degradation of $T_2^ \ast$

We observed that the difference between the “No switching pulse with maximal coupling” and “Switching pulse tuned to turn off the coupling” situations is 9.57 compared with 15.25 for the “2” and “3” situations, this is because the relaxation time of Q₂ is 7.0 μs, shorter than that of Q₁ (15.58 μs). Further, it is quite interesting that the decay behavior between the “1” and “3” situations are almost the same, even if we attribute all the slight difference to a weak, residual coupling, it should be less than 2.7 kHz (see Methods). The lower limit of the on/off ratio is g/g_r = 0.61 MHz/2.7 kHz ~230, where g is the coupling strength between the two qubits. Further, the on/off ratio could be significantly enhanced by improving the qubit coherent properties and the precision of the control pulse, since the effective coupling g_eff = gJ₀(2λ_z/ω_z) can be tuned from positive to negative crossing the zero point. Also, as can be seen in the Methods section (Fig. 6) the numerical simulation shows an on–off ratio higher than 10⁵, which hightlights the potential of the longitudinal control field as a high-efficiency way to turn off the coupling.

While we have shown that our longitudinal pulse enables an effective switching operation, it is important to establish its effect on the quantum coherence of the systems. To this end we will now demonstrate the dynamical switching on and off of the coupling. In this case a target qubit is initially prepared in its excited state and brought into coherent resonance with its corresponding quantum element, after a delay, a switch-off pulse is applied over a period of time. In Fig. 4a, d, the coupling is switched off when the target qubit is in the excited state. In Fig. 4b, e, the coupling is switched off when the system is in an entangled state. In Fig. 4c, f, the coupling is switched off when the target qubit is on the ground state. We found that regardless of what state the system is in, when the switch-off pulse is applied, the coherent oscillation is paused (except for free evolution and decay during the switch-off time interval), and when the switch-off pulse is removed, the coherent oscillation resumes.

Fig. 4

Dynamics of switching on/off the coupling. The qubit Q₁ is initially prepared in its excited state and allowed to interact with either the second qubit (in the case of the qubit–qubit configuration) or the resonator (in the flux qubit configuration). At a certain time, a switch-off pulse is applied, freezing the coherent oscillation between the two systems. At a later time, the switching pulse is removed and coherent oscillation resumes. In a, d the switch-off pulse is applied when the first qubit is in its excited state, while in b, e the coupling is switched off when Q₁ and either Q₂ or the resonator are in an entangled state. Finally, for c, f the coupling is switched off when Q₁ is in the ground state. Solid lines are simulations with measured energy relaxation times, 15.6 μs for Q₁ and 7.0 μs for Q₂ in the qubit-qubit system, 0.45 μs for the qubit and 4.6 μs for the resonator in the flux qubit system. a-c is the data for the qubit-qubit system while d-f is the data for the qubit-resonator system

Discussion

We have demonstrated a highly efficient switch with an rf control field, the coupling strength can be in principle tuned to zero in both a qubit–qubit system and a qubit–resonator system. Dynamically switching on and off the coupling is also shown. The on–off ratio was measured to be above 230, and could be significantly improved in the future. In principle, the coulping could also be modified from g to any value in the range [−0.4g, g], which allows the system dynamics to be retarded or reversed. This could be useful in spin–echo-like refocusing appliactions. This type of switch scheme can be applied to any qubit system with longitudinal control field and scales easily since no auxiliary circuit is needed. For applications to N qubits, we have done a preliminary investigation for cases with nearest-neighboring coupling. For the case of 1-D chain qubits with nearest-neighboring coupling, our numerical simulations show that by applying driving fields on every other qubit, couplings can be switched off when all N qubits are at the same qubit frequency. Scaling up to 2-D configurations is also straightforward. We also point out that besides as a tunable coupling scheme between quantum elements, the longitudinal coupling and control between electromagnetic fields and quantum devices itself is of great interest.^56–63

Methods

The qubit–qubit sample

This sample consists of six qubits fabricated with aluminum evaporation and lift-off techniques. The Josephson junctions are formed by using the Dolan bridge technique. The two qubits on which we perform the experiments are interconnected by a coplanar resonator, which couples them dispersively, the resonator has a resonance frequency about 5.45 GHz, well above the qubit frequencies. The T₁ of the two measured qubits are approximately 14 and 7 μs, while $T_2^ \ast$ is ~7 μs for both qubits.

The qubit–resonator system

The sample is a gap-tunable flux qubit inductively coupled to a λ/4 coplanar resonator. A flux qubit is a superconducting loop interrupted by three Josephson junctions. Two of them are of the same size, and the other is smaller by a factor of α (α < 1). The larger two are characterized by Josephson energy E_J and charge energy E_c.The qubit states correspond to clockwise and counter-clockwise persistent currents ±I_p in the qubit loop, I_p ≈ 400 nA in our sample. When the magnetic flux bias in the qubit loop Φ_ε = Φ₀/2, called the optimal point, the two persistent-current states are degenerate, quantum tunneling lifts this degeneracy, forming an energy gap ħΔ. Once E_J and E_c are fixed, the energy gap of a flux qubit is determined by α, the ratio of critical current between the smaller and larger junctions. Since the resonator frequency is fixed, and since there exists an optimal point of coupling between the qubit and resonator where the coherence properities of the system are the best, it is desirable to have the energy gap tunable. In our sample, the smaller junction has been replaced by a dc-SQUID, called the the α-loop, making the energy gap tunable in a wide range. The longitudinal control pulse for switching on/off the coupling is also applied to the qubit through the α-loop. To achieve high magnetic flux bias stability, we use a gradiometric design for the qubit loop, making the qubit insensitive to global flux fluctuations. The qubit state is detected by a readout dc-SQUID inductively coupled to the qubit. The sample is fabricated on a silicon wafer using electron beam lithography patterning, aluminum evaporation, and lift-off techniques. Josephson junctions are formed by using the Dolan bridge technique. The relaxation times of the qubit and the resonator are 0.45 and 4.6 μs, respectively.

Determination of the measured switch efficiency

In the case of the “Single-qubit energy relaxation” of Fig. 3b (Case 1), the relaxation time was measured as T = 15.58 ± 0.28 μs, while in the case of the “switching pulse tuned to turn off the coupling” (Case 3), the relaxation time was T = 15.25 ± 0.24 μs. Using the worst case after 14 μs decay, the 95% confidence upper bound of case 1 and the lower bound of case 3, the population ratio between case 3 and case 1 is 0.89. If we attribute the entire population drop to the residual coupling, the upper limit of oscillation frequency induced by the residual coupling is 2g_r = arccos(0.89)/(14 μs/2π) = 2.7 kHz.

Model of the qubit–qubit system

Our full system can be described by the Hamiltonian

$$H(t) = H_0 + H_I + H_L,$$

(4)

with

$$H_0 = \frac{\hbar }{2}\omega _1\sigma _{z,1} + \frac{\hbar }{2}\omega _2\sigma _{z,2}$$

(5)

$$H_I = \hbar g\left( {\sigma _{ + ,1}\sigma _{ - ,2} + \sigma _{ - ,1}\sigma _{ + ,2}} \right),$$

(6)

$$H_L = \hbar \lambda _z\sigma _{z,1}{\kern 1pt} {\mathrm{cos}}\omega _zt,$$

(7)

Here, H₀ describes the free Hamiltonian of the two qubits with $\sigma _{z,i} = \left| {e_i} \right\rangle \left\langle {e_i} \right| - \left| {g_i} \right\rangle \left\langle {g_i} \right|$ being the Pauli matrix with the excited $\left| {e_i} \right\rangle$ and ground $\left| {g_i} \right\rangle$ states of the ith qubit. The interaction between the qubits is given by H_I, where g is the qubit–qubit coupling strength. Finally, the longitudinal driving field applied to qubit 1 is given by the Hamiltonian H_L where λ_z is the amplitude of that field. We will also assume the coupling strength g is much smaller than the frequency of the control field ($g \ll \omega _z$).

Moving to an interaction picture with respect to H₀ + H_L, our resulting Hamiltonian can be written in the form

$$H_I = \hbar g\left[ {{\mathrm{exp}}\left( {i\frac{{2\lambda _z}}{{\omega _z}}{\mathrm{sin}}{\kern 1pt} \omega _zt} \right)\sigma _{ + ,1}\sigma _{ - ,2} + {\mathrm{h}}{\mathrm{.c}}{\mathrm{.}}} \right],$$

(8)

$$= \hbar g\mathop {\sum}\limits_{n = - \infty }^\infty \left[ {J_n\left( {\frac{{2\lambda _z}}{{\omega _z}}} \right)e^{in\omega _zt}\sigma _{ + ,1}\sigma _{ - ,2} + {\mathrm{h}}{\mathrm{.c}}{\mathrm{.}}} \right],$$

(9)

where we have used the Jacobi–Anger expansion and J_n(x) is the Bessel function of the first kind. As $gJ_{n \ne 0}\left( {2\lambda _z{\mathrm{/}}\omega _z} \right) \ll \omega _z$, the nonresonant terms (n ≠ 0) can be neglected and the interaction between the qubits is reduced to

$$H_I \approx \hbar g_{{\mathrm{eff}}}\sigma _{ + ,1}\sigma _{ - ,2} + {\mathrm{h}}{\mathrm{.c}}{\mathrm{.,}}$$

(10)

with the effective coupling strength g_eff = gJ₀(2λ_z/ω_z). When the ratio 2λ_z/ω_z reaches the first zero point of the Bessel function J₀(x) near x ≈ 2.4, the qubits are effectively decoupled. We call this point λ_z,off the switch-off point. The fast oscillation terms neglected above result in a small oscillation on the qubit–qubit state when the qubit- qubit coupling is switched off. The amplitude of this oscillation decreases rapidly with increasing ω_z.

Model for the flux qubit–resonator system

The derivation of an effective Hamiltonian of the form

$$H_I \approx \hbar gJ_0\left( {2\lambda _z{\mathrm{/}}\omega _z} \right)\sigma _{ + ,1}\;a + {\mathrm{h}}{\mathrm{.c}}.,$$

(11)

follows in a similar fashion to the qubit–qubit systems derivation where one simply replaces the second qubit $\frac{\hbar }{2}\omega _2\sigma _{z,2}$ with a harmonic oscillator $\hbar \omega _ra^\dagger a$ and that qubit’s raising and lower operators with the bosonic creation/destruction operators.

Numerical simulations

The time evolution of our system including dissipation can be described by the Lindblad Markov master equation

$$\frac{{d\rho }}{{dt}} = - \frac{i}{\hbar }[H,\rho (t)] + ({\cal L}_{qb}[\rho ] + {\cal L}_r[\rho ]),$$

(12)

where

$$\begin{array}{*{20}{l}} {{\cal L}_{qb}[\rho ]} \hfill & = \hfill & {\gamma _{qb}\left[ {N\left( {\omega _q} \right) + 1} \right]\left[ {\sigma _ - \rho \sigma _ + - \frac{1}{2}\sigma _ + \sigma _ - \rho - \frac{1}{2}\rho \sigma _ + \sigma _ - } \right]} \hfill \\ {} \hfill & {} \hfill & { + \gamma _{qb}N\left( {\omega _q} \right)\left[ {\sigma _ + \rho \sigma _ - - \frac{1}{2}\sigma _ - \sigma _ + \rho - \frac{1}{2}\rho \sigma _ - \sigma _ + } \right],} \hfill \\ {{\cal L}_r\rho } \hfill & = \hfill & {\gamma _r\left[ {N\left( {\omega _r} \right) + 1} \right]\left[ {a\rho a^\dagger - \frac{1}{2}a^\dagger a\rho - \frac{1}{2}\rho a^\dagger a} \right]} \hfill \\ {} \hfill & {} \hfill & { + \gamma _rN\left( {\omega _r} \right)\left[ {a^\dagger \rho a - \frac{1}{2}aa^\dagger \rho - \frac{1}{2}\rho aa^\dagger } \right],} \hfill \end{array}$$

where γ_qb and γ_r are the decay rates of the qubit and the resonator, respectively. N(ω) = 1/[exp(βħω) − 1] is the average occupation number of the bath mode with the frequency ω at the temperature T with β = 1/(k_BT). In the experiment, measurements are taken in a dilution refrigerator at temperature T ≲ 20 mK. For ω_qb/2π = ω_r/2π = 2.417 GHz, the temperature of the bath can taken as 0, since N(ω_qb) and N(ω_r) are less than 0.003.

In the experiment, the system is initialized in the ground state $\left| {g,0} \right\rangle$ and a weak, transverse probe field with frequency ω is applied to detect the spectrum of the coupled system. The detected spectrum intensity is proportional to the integral of the probability P(t) of the qubit being in the excited state over a fixed time interval:

$$I \propto {\int}_0^t {\kern 1pt} P(t)dt,$$

(13)

where

$$P(t) = \frac{1}{2}\left[ {1 + \left\langle {\sigma _z(t)} \right\rangle } \right].$$

(14)

The schematic of the four lowest energy levels of the coupled system is shown Fig. 5a. Due to the coupling between the qubit and the resonator, the lowest two excited states of the system $\left| \pm \right\rangle = \left( {\left| {e,0} \right\rangle \pm \left| {g,1} \right\rangle } \right){\mathrm{/}}\sqrt 2$ are separated with a gap ~2g_eff. As shown in Fig. 5b when the amplitude of the control field λ_z = 0, the resonance absorption peaks corresponding to the transitions [denoted by the blue arrows in Fig. 5a] between the ground state $\left| {g,0} \right\rangle$ and the lowest two excited states $\left| \pm \right\rangle$ locate at δ = ω_qb − ω = ±g. As the amplitude λ_z of the control field increases, the gap first decreases and then vanishes at the switch point (λ_z ≈ 1.2ω_z), since the coupling between the qubit and the resonator is almost switched off. When λ_z > 1.2ω_z, the coupling is switched on again and the gap increases with λ_z. The coupling between the qubit and the resonator is switched off again when x = 2λ_z/ω_z reaches the second zero point of the Bessel function J₀(x).

Fig. 5

a The schematic of the four lowest energy levels of the coupled system is shown. The energy gap between states $\left| \pm \right\rangle$ is 2g_eff if the qubit is resonant with the resonator, i.e., ω_qb = ω_r. b The absorption spectrum of the coupled system is presented. The two absorption peaks correspond to two resonant transitions, denoted by the blue arrows in a. The strength of the coupling between the qubit and the resonator is about g/2π = 9.14 MHz, and the frequency of the controlling field is ω_z/2π = 150 MHz. The decay rates of the qubit and the resonator are about γ_qb = 0.35 MHz (corresponding T₁ = 450 ns) and γ_r = 0.035 MHz (corresponding T₁ = 4.6 μs), respectively. c The occupation probability P of the qubit vs. time and the strength λ_z of the control field are displayed. Here, the system is initialized in the state $\left| {e,0} \right\rangle$. When no control field is applied (λ_z = 0), P oscillates with time in period T_R = 2π/g (Rabi oscillation). The control field diminishes the effective coupling strength and elongates the period of the Rabi oscillation. At the switch point, the coupling between the qubit and resonator is effectively switched off and the Rabi oscillation disappears. When λ_z goes beyond this point, the coupling is switched on again and Rabi oscillation recovers

When the decay rates of the qubit and the resonator satisfy $\gamma _{q(r)} < g \ll \omega _{q(r)}$, the first two excited states $\left| \pm \right\rangle$ form a quasi-invariant subspace. If the system is initially in the state $|e0\rangle _{}^{}$, a Rabi oscillation induced by the qubit–resonator coupling is observed as shown in Fig. 5c. When the amplitude of the control field is zero, the period of the Rabi oscillation is T_R = 2π/g. When the strength of the control field increases, the effective coupling strength decreases and the period T_R,eff of the Rabi oscillation becomes longer. At the switch point, the coupling between the qubit and resonator is effectively switched off and the Rabi oscillation disappears.

Mathematical model example

Assume the system to be initialized in the state $\left| {\psi (0)} \right\rangle = \left| e \right\rangle \otimes \left| 0 \right\rangle$ with the qubit in its excited state and the resonator is in the vacuum state.

If no longitudinal control field is applied to the qubit (i.e., λ_z = 0), the Rabi oscillation between the qubit and the resonator takes place in the single-excitation subspace $\left\{ {\left| {e,0} \right\rangle ,\left| {g,1} \right\rangle } \right\}$. The period of this Rabi oscillation is T_R = π/g. After the control field is applied, the effective coupling between the qubit and the resonator is suppressed and almost eliminated at the switch-off point λ_z/ω_z ≈ 1.2. Correspondingly, the period of the effective Rabi oscillation T_R,eff around the switch-off point is prolonged greatly by the control field, as shown in Fig. 6a. Now, we define the on/off ratio as

$$R = \frac{{T_{R,{\mathrm{eff}}}}}{{T_R}}.$$

(15)

Fig. 6

a The probabilities P of the qubit at the excited state as a function of time. The whole system is initially in the state $\left| {0,e} \right\rangle$ and an effective Rabi oscillation is observed. Here, the coupling strength between the qubit and resonator is g/2π = 9.14 MHz and the amplitude of the control field is around the switch-off point λ_z/ω_z ≈ 1.2. The period of the effective Rabi oscillation is prolonged greatly, i.e., T_R,eff/T_R ≈ 4.5 × 10⁻⁶. b The on/off ratio R as a function of λ_z/ω_z is displayed

Numerical simulations show that the period of the effective Rabi oscillation changes drastically near the switch-off point [see Fig. 6a]. The on/off ratio R as a function of the amplitude λ_z of the control field is displayed in Fig. 6b. We find that R decreases drastically when λ_z approaches the switch-off point λ_z ≈ 1.2ω_z, which is slightly smaller than the one that matches the zero point of the Bessel function J₀(2λ_z/ω_z). So if the amplitude λ_z of the control field can be precisely manipulated, the coupling between the qubit and the resonator can be effectively switched off by the longitudinal field, i.e., R < 10⁻⁵.