Introduction

The ability to precisely control and calibrate single qubit operations in solids is a key element for reliable and scalable high-performance quantum technologies, for instance quantum-enhanced sensors and metrological devices. It is also the backbone of many quantum information processing tasks, which paves the way for the future realisation of quantum computation and communication. Together with efficient quantum system characterisations and dynamical predictions,1,2 where human intervention is minimised, autonomous calibration of a single spin qubit is necessary for the realisation of such advanced quantum technologies. We report here experimental demonstrations of the autonomous calibration of a single spin qubit in diamond using closed-loop optimisation. Our spin qubit implementation is a single nitrogen-vacancy (NV) colour centre in diamond. It provides a suitable platform for a precise qubit manipulation to be realised.3,4 Its remarkable features, such as optical initialisation and readout, and the ability to be manipulated by microwave fields at room temperature, make this physical system extremely attractive for many quantum technologies.5 We have witnessed a vast array of demonstrations of the NV centres showing a great potential for future technologies, ranging from sub pico-Tesla magnetometry,6 electric field and temperature sensing,7,8 to probing molecular dynamics,9 and single-cell magnetic imaging.10 Furthermore, intertwinements between quantum information and metrology using NV centre-based systems yield novel and effective techniques towards the realisation of high-performance technologies, e.g. applying quantum error correction11 and phase estimation12 to improve magnetic field sensitivity. One way to reach such technology is to apply the closed-loop optimisation method for auto-calibrating the controls required to drive the system in the presence of experimental limitations and noise. Closed-loop optimal control has been already applied to quantum information processing.13,14 However, to date no realisation of such autonomous calibration in room-temperature solids has been reported. Here, we apply a technique derived from optimal control theory, namely the dressed chopped random basis (DCRAB) algorithm,15,16 to perform real-time closed-loop optimisations of two fundamental single qubit operations, a spin-1/2 population inversion and a \(\frac{\pi }{2}\)-rotation gate, against frequency detuning. The algorithm is adapted for use in the NV centre-based experiment and directly embedded in the experimental apparatus, allowing the autonomous spin qubit calibrations to be fully performed as illustrated by Fig. 1. In contrast to a simple feedback circuit where usually only a single degree of freedom is adjusted at a time based on continuous measurement, our framework considers the whole quantum dynamics and is capable of addressing multiple degrees of freedom at every instance in time.

Fig. 1
figure 1

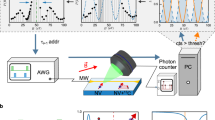
Schematics of the experiment. The closed-loop optimisation of electron spin qubit operations interfaced to a nitrogen-vacancy (NV) centre in diamond (nitrogen atom in yellow) a is performed on a homebuilt confocal microscope c. The spin state is initialised and readout optically, and microwave pulses are applied to manipulate the state and can be used to create gates. To start an optimisation process, a guess pulse is applied to the sample through a microwave antenna and the figure of merit is evaluated by state tomography on the spin state. This fidelity estimate is then fed to an DCRAB based algorithm and a new test-pulse is generated. The spin trajectory (blue arrow) corresponding to an optimised pulse is shown on the Bloch sphere b. As sketched, these steps are iteratively repeated until a previously definded fidelity is reached

Full size image

Optimal control methods have been applied to several quantum information processing tasks with NV centres,17,18,19,20,21,22 affirming their necessity and significance for quantum technology. However, the previously reported experiments,17,18,19,20,21,22 utilise open-loop optimisation techniques where the optimisation is performed before the actual experiment by separate computer simulations. The technique requires system–environment coupling information as detailed as possible to provide a robust solution. In contrast, the closed-loop technique requires no explicit system–environment information. Hence, it is utmost practical for the realisation of versatile quantum devices. One significant feature of the DCRAB algorithm is that it makes such closed-loop optimisation viable since the only quantity required from the experiment is a single figure of merit (e.g. state or gate fidelity). No further information, such as a gradient or a Hessian, is necessary. Moreover, recent theoretical work,23,24 points out that the relevant number of degrees of freedom in the control is rather small for few qubit systems. A reasonable number of degrees of freedom can be addressed through a suitable parametrisation.25,26,27 The DCRAB algorithm makes use of this foundation. It shapes high accuracy pulses with few iterations (or superiteration that is required for avoiding local optimisation traps), and maintains the robustness against noise and errors potentially occurred at any stage of experiments.16 The key ideas are to expand the pulses in a reasonable function basis and subsequent basis function changes to avoid local traps. We provide more detailed discussions of the algorithm and its implementations in the “Methods” section and in Section A in the Supplementary Material.

Results

High fidelity population inversion via closed-loop control

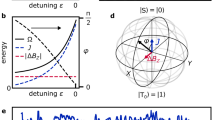
In this experiment, we search for an optimal microwave pulse to transfer the NV spin state \(\left| {m_{\rm s} = 0} \right\rangle\) to \(\left| {m_{\rm s} = - 1} \right\rangle\) with high fidelity. Therefore, we performed a state tomography after applying a parametrised microwave pulse. Subsequent measurement of the state transfer fidelity is then used as a figure of merit. To estimate the particular fidelity \(F_{{\rm ex}}^{{\rm cl}}\) we utilised quantum state tomography (see Sections B and C of the Supplementary Information). For convention, the subscripts of the fidelity \(F_i^j\) indicate either experimental (ex) or theoretical (th) data. The superscripts (cl) and (ol) refer to closed-loop and open-loop control, respectively. In Fig. 2 we show the results of our state transfer optimisation. In part (a), we first identify via an open-loop simulation the expected performance of the employed optimisation method in presence of limited transfer time T and static detuning Δ. For relative process times T/T π exceeding ~1.5, our simulations identify robust solutions even up to a relative detuning of about \(\frac{{\mathrm{\Delta }}}{{\mathrm{\Omega }}} = 10\). Here the maximal Rabi frequency is determined by \({\mathrm{\Omega }} = \frac{1}{{2T_\pi }}\), which is connected to the maximal amplitude of the applied microwave pulse. We studied transfer times in the regime T/T π  > 1 because the maximum speed of a quantum system evolution is bound in general by the quantum speed limit.28,29 Numerical simulations support this fact when a rectangular microwave pulse shape is assumed (see Supplementary Material Section G). In part (b), we show our experimental results achieved via closed loop optimisation, which support these results for small detuning, when T/T π  = 1.5. For comparison, we show the corresponding cross-section of the numerical results of part (a) in (c). Each optimisation, performed for a certain gate time and a certain detuning, bases on a DCRAB algorithm with six superiterations. Exemplarily, we show in Fig. 2d, e the full closed-loop optimisation process in the case of no detuning, and when a small detuning is applied. The blue curve shows the currently best found solution, while the red line is an internal algorithmic figure of merit quantity (for details see Supplementary Material Section A). The necessary time for achieving optimal fidelities depends on the accuracy of the tomography measurements \(\left( {F_{{\rm ex}}^{{\rm cl}}} \right)\) and on the initial optimisation parameters. In our case, a randomly chosen configuration (start-simplex) of the search algorithm was used. We achieve the maximal fidelity of 1.00 with an accuracy of 10−2 on a reliable timescale of about 2000 s in the case of no detuning and on a timescale of about 100 s with detuning. A faster optimisation with an off-resonant pulse is here possible due to a fortunate choice of the initial search-configuration (optimal solution was already part of start-simplex). It is interesting to note, that all optimised pulses of the open-loop simulation were not able to beat the results of our closed-loop strategy in the case of moderate detuning. The best fidelity achieved via open-loop techniques \(\left( {F_{{\rm th}}^{{\rm ol}}} \right)\) is marked in Fig. 2b and is only on the order of 0.6.

Fig. 2
figure 2

Optimal state transfer in presence of frequency detuning and limited time resources. a shows the resulting fidelity \(\left( {F_{{\rm ol}}^{{\rm th}}} \right)\) from the parameter study of the optimised state transfer as a function of relative process time \(\frac{T}{{T_\pi }}\) and rel. detuning \(\frac{{\mathrm{\Delta }}}{{\mathrm{\Omega }}}\). T is the time duration of the applied pulse and T π is the time necessary for a population inversion when a constant Rabi frequency of Ω is applied. Δ is the detuning of the microwave frequency. In b we show the results of the closed-loop experimental optimisation (\(F_{{\rm cl}}^{{\rm ex}}\), red points) for different rel. detuning and a fixed transfer time of \(\frac{T}{{T_\pi }} = 1.5\). In addition, the level of best achieved fidelities from experimental evaluation of open-loop pulses is indicated (by black dashed line). A cross-section of the theoretical results from a at \(\frac{T}{{T_\pi }} = 1.5\) is shown in c. d shows the evaluated fidelities \(\left( {F_{{\rm cl}}^{{\rm ex}}} \right)\) when the microwave pulse is applied on resonance and in e when a relative detuning of 0.2 is applied. The blue lines show the last, highest fidelity achieved

Full size image

Auto-calibration of a single qubit \(\frac{\pi }{2}\)-rotation

A \(\frac{\pi }{2}\)-rotation is the basic block of generating coherent quantum processes-like quantum metrology and quantum computing. To show the capabilities of our concept, we subsequently optimised the quantum gate

$$G = e^{ - i\frac{\pi }{2}S_x} = \frac{1}{{\sqrt 2 }}\left( {\begin{array}{*{20}{c}} 1 & { - i} \\ { - i} & 1 \end{array}} \right),$$
(1)

which is a typical experimental implementation of a Hadamard gate. Here, S x identifies the spin-\(\frac{1}{2}\) x-operator. In accordance to the previous experiment, we first performed the experiment with no detuning and second, when a detuning of 8.125 MHz (relative detuning \(\frac{{\mathrm{\Delta }}}{{\mathrm{\Omega }}} = 0.7\)) was applied. The results are shown in Fig. 3. To quantify the performance of the evaluated microwave pulse with respect to the defined quantum gate G, quantum process tomography was used (for details see Supplementary Material Sections D and E). We observe after 99 evaluations a fidelity of 0.99 ± 0.01 and after 58 evaluations a fidelity of 0.98 ± 0.02 when the static microwave detuning was applied. The initial fidelity of the guess pulse was in both cases about 0.50. Compared to the previous experiment, the time needed for optimal results is about four times longer due to additional measurements, which are necessary for complete process tomography.

Fig. 3
figure 3

Optimisation of a single qubit π/2-rotation when the control pulse is applied on resonance with the NV transition a and when a detuning on the order of the Rabi frequency is artificially applied b. For each scenario we show the measured fidelity \(F_{{\rm ex}}^{{\rm cl}}\) with increasing number of function evaluations and the experimentally obtained process matrix for the real (left) and the imaginary part (right) in case of the highest evaluated fidelity

Full size image

Discussions

Our experimental results demonstrate that the closed-loop feedback control overcomes static and unknown system errors to achieve the high-fidelity autonomous calibration of single quantum gates that is necessary for future quantum technologies with room temperature solids. Our approach of the closed-loop optimisation uses minimal control resources and experimental knowledge that are accessible for users. The total time, required for autonomous calibration, is mainly determined by the duration of quantum tomography measurement and not by the optimisation algorithm. Hence, a significant speed up in the total time of calibration and its fidelity precision may potentially be achieved by employing fast and simplified tomography methods, for instance randomised benchmarking.30 In addition to the autonomous calibration, our demonstrated closed-loop optimisation features stabilisation mechanism against experimental drifts, for instance due to fluctuations of the magnetic field strength and the resulting frequency detuning. Our procedure presented in this letter is not limited for application to single-qubit operations only. Further experimental implementations towards multi-pulse and multi-qubit gate autonomous calibrations are in principle feasible using our closed-loop optimisation method. Two qubit gates are often experimentally implemented with multiple pulses. In this case, each pulse could be parametrised individually or the overall pulse sequence can be parametrised by a proper basis function choice. The complexity will in general increase due to a more complex quantum process tomography or due to a larger parameter space. But the protocol itself, evaluation of a pulse sequence gate fidelity followed by a systematic pulse sequence update, can readily be extended as the algorithm does not require any a priori system knowledge and is therefore flexible in its use.

Methods

The two-level quantum system considered in this work is composed of the NV ground spin states \(\left| {m_{\rm s} = 0} \right\rangle\) and \(\left| {m_{\rm s} = - 1} \right\rangle\). Electron spin initialisation and readout are performed on a home built confocal microscopy setup at room temperature. To perform quantum operations on the NV spin with high fidelity, the microwave field source is controlled by an arbitrary waveform generator (AWG, Keysight M8195A), with a timing resolution of 65 GS/s and an amplitude resolution of 8 bit. In combination, we used a 50 W amplifier with a frequency bandwidth of about 4 GHz. The microwave field was created with a copper wire close to the NV. By controlling the amplitude and the phase of the microwave, we are able to rotate the system spin around arbitrary axis on the Bloch sphere. The time-dependent control Hamiltonian is given by

$$H_{\rm c} = 2\pi {\mathrm{\Omega }}\left( {X(t)\hat S_x + Y(t)\hat S_y} \right),$$
(2)

while the system Hamiltonian in the rotating frame is \(H_0 = 2\pi {\mathrm{\Delta }}\hat S_z,\) where \(\hat S_x\), \(\hat S_y\), and \(\hat S_z\) are the spin operator of a two-level system. The functions X(t) and Y(t) define the corresponding microwave pulse, where Ω is the Rabi frequency and Δ is the microwave frequency detuning. In our experiments the following conditions were fulfilled:

$$X(t) + Y(t) \in \left[ { - 1 1} \right],{\mathrm{\Omega }} \in \left[ {0 10} \right]({\mathrm{in}}\,{\mathrm{MHz}}).$$
(3)

The two functions X(t) and Y(t) are optimised simultaneously using the DCRAB algorithm, where both start off from an initial guess (randomly chosen start-simplex). At the core of the algorithm there is the use of superiterations, which are composed again of an iterative update scheme that maps the time dynamics of all control input variables to a parameter variational problem via a suitable basis expansion. A brief introduction along with more general explanations can be found in SI/A. In this work, X(t) and Y(t) were expanded in (sub-) iteration denoted by j of each superiteration denoted by k as

$$\begin{array}{*{20}{l}} {X(t)^{*,k}} \hfill & \hskip-8pt = \hfill &\hskip-7pt {a_{n = 1}^{\,j,k}\,{\rm sin}\left( {\omega _{n = 1}^{\,j,k}t} \right)} \hfill \\ {} \hfill & {} \hfill & { + b_{n = 1}^{\,j,k}\,{{{\rm cos}}}\left( {\omega _{n = 1}^{\,j,k}t} \right) + X(t)^{*,k - 1}}, \hfill \end{array}$$
(4)
$$\begin{array}{*{20}{l}} {Y(t)^{*,k}} \hfill & \hskip-8pt = \hfill &\hskip-7pt {c_{n = 1}^{\,j,k}\,{{{\rm sin}}}\left( {{\mathrm{\Omega }}_{n = 1}^{\,j,k}t} \right)} \hfill \\ {} \hfill & {} \hfill & { + d_{n = 1}^{\,j,k}\,{{{\rm cos}}}\left( {{\mathrm{\Omega }}_{n = 1}^{\,j,k}t} \right) + Y(t)^{*,k - 1}.} \hfill \end{array}$$
(5)

The two frequencies \(\omega _{n = 1}^{\,j,k} \in [0.5 4.5]\) and \({\mathrm{\Omega }}_{n = 1}^{\,j,k} \in [0.5 4.5]\) are randomly chosen at the beginning of each superiteration k and only updated after all the containing j = 1,...,N s (sub-) iterations were proceeded. This is where, in our case, the four coefficients \(a_{n = 1}^{\,j,k},b_{n = 1}^{\,j,k},c_{n = 1}^{\,j,k},d_{n = 1}^{\,j,k}\) are optimised using a direct search method (here Nelder–Mead, see Supplementary Material Section A). When j = N s and thus a (sub-) iteration terminates, a basis update is done by updating (re-drawing of random numbers) \(\omega _{n = 1}^{\,j,k}\) and \(\Omega _{n = 1}^{\,j,k}\) and hence facilitating further improvement (see also Supplementary Material/Fig. 2). The subsequent super-iteration (k + 1) search bases on the previous superiteration by calculating X(t)/Y(t)*,k−1 with the optimised (denoted by *) coefficients \(a_{n = 1}^{*,k},b_{n = 1}^{*,k},c_{n = 1}^{*,k},d_{n = 1}^{*,k}\) from the previous kth superiteration. The algorithm terminates once the maximum number of superiterations set is reached.

Data availability

The authors declare that the main data supporting the finding of this study are available within the article and its Supplementary Information files. Additional data can be provided upon request.

Code availability

The code that contributed to the results of this study is available on request from the authors.