Introduction

Thermodynamics is one of the pillars of physical, chemical, and biological sciences.1 It predicts and explains the occurrence and efficiency of complex chemical reactions and biological processes. In physics and engineering, the conduction of heat across a medium, the concept of the arrow of time,2, 3 and the efficiency of motors are formulated in thermodynamic terms.4,5,6,7 In information theory, the mantra that “information is physical” simply entails that, by being encoded in physical supports, information must obey the laws of thermodynamics.8, 9 Even more, the tightness of the link between information and thermodynamics can be appreciated from the thermodynamic interpretation of the landmark embodied by Landauer’s erasure principle,10 Jaynes principle of maximum entropy,11, 12 or the information theoretical exorcism of Maxwell’s Demon operated by Charlie Bennett.13,14,15 More recently, it has been realized that thermodynamics can be used to provide a new way of assessing and exploiting quantum dynamics, build super-efficient nano-engines and micro-engines that take advantage of quantum coherence, and assess information theory from the perspective of thermodynamic costs.16,17,18,19

The identification of the specific features of quantum systems that might influence their thermodynamic performance is still an open challenge20, 21: quite controversially, perfectly reversible work extraction from an ensemble of non-interacting quantum information carriers appears to be possible without the need for creating any entanglement.22 Moreover, while entangling quantum operations allow for the retrieval of the same amount of work as in the classical case but with more economic protocols, such advantage appear to fade away in the case of a large number of systems.23

Within such an interesting quest for the origin of “quantumness” in quantum thermodynamics, a core achievement is represented by thermodynamics-inspired witness of (multipartite) entanglement in a working medium.24, 25 Such criteria can be cast as Bell-like games, in which the payoffs do correspond univocally to thermodynamics-inspired quantities. Having in mind the Szilard engine-version of Maxwell’s paradox, one can build one such game, corresponding to an enhanced extractable work from an hypothetical heat bath when using an entangled working medium. This all provides thermodynamic-inspired inequalities that are satisfied by any separable state of the working medium, but are violated by entangled states.

Such approaches to inseparability in the case of physical working media prepared in quantum laboratories have not yet been addressed due to the scarcity of experiments addressing the quantum thermodynamic framework, of which we only have a handful to date.26,27,28,29,30

Results

Here, we bridge this gap by investigating experimentally thermodynamics-based separability criteria using non-ideal entangled two-qubit and three-qubit quantum working media. We demonstrate the attainability of a maximal violation of the thermodynamic separability criterion, which would be thus equivalent to the achievement of the maximal extractable work allowed by the availability of non-classical correlations. The similarity between the realization of the game on the basis of the thermodynamic inseparability criterion studied here and Bell-like tests allow for the comparison between such approaches to the characterization of quantum correlations. We experimentally show that non-classical correlations empowering the extractable work bear differences to those responsible for the violation of Bell-type inequalities. We believe that, through so far unexplored theoretical tools, our results pioneer novel experimental methods toward the understanding of how non-classical correlations can effect the efficiency of quantum thermodynamic processes, at equal footing with thermodynamic potentials. This is a topical problem of both foundational and pragmatic relevance for the development of future engines operating at the nanoscale and in the fully quantum regime.

Let us set the thermodynamic context that serves the basis for the interpretation of the thermodynamic criterion for separability. Consider a single-particle gas in a Szilard machine-like device, i.e., a split chamber that be put in contact with a thermal reservoir at temperature T. By determining whether the particle occupies the left or right half-chamber, we can extract \({k_B}T\ln 2\) of work out of the reservoir simply by letting the gas equilibrate with it (isothermally). Here, k B is Boltzmann’s constant. Suppose now that only partial information about the position of the particle in the chamber is available. In this case, the work that could in principle be extracted is \(({k_B}T\,\ln \,2)[1 - H(X)]\), where H(X) is the Shannon entropy of the binary position X of the particle.24 Here, \({k_B}T\,\ln \,2\) is a single scaling factor whose inclusion little adds to the physics of the problem. From here on, we thus rescale work in units of \({k_B}T\,\ln \,2\), and focus solely on the “information-theoretical” gain 1−H(X), which encompasses the core of the extractable-work scheme illustrated here. In this sense, while it should now be clear that we are addressing explicitly an information-thermodynamic problem, we can elevate the reservoir at the role of a virtual entity with limited physical relevance in the context here illustrated, besides the establishment of a “gauge” for the quantification of extractable work.

Let us now extend the scenario to the quantum domain and use projective operations to acquire information on the state of a two-level system that embodies the counterpart of the one-particle gas in the split chamber. In this case, we can store the measurement results in classical bits, so that the same process as above can be applied. Clearly, the entropy H(X) is associated to the outcomes of a measurement on a two-level state. The work that could be extracted is then associated purely to the measurement and not to the dynamics of the state. This allows us to focus on the information brought about by the state of the system, rather than the implementation of an actual protocol for the extraction.

Moving from the single-particle to the bipartite case, we take inspiration from the fact that Maxwell had in mind Greek daimones, i.e., powerful entities bridging the human and the divine. We shall thus formulate our approach in the language of a general game involving two daemons, Aletheia (Aλήθεια) and Bia (Bία), each attempting at extracting work from a two-qubit system.

They share an ensemble of qubit pairs, each prepared in the same bipartite state ρ. Moreover, they agree on the choice of two sets of measurement operators (one per daemon) that densely cover a great circle on the Bloch sphere of a single qubit. For half of the ensemble, Aletheia should choose from the set \(\{ {\hat A_\theta }\} \), the projection operator to use in order to measure her qubit. For the remaining half of the ensemble, Bia shall pick her measurement operator from the set \(\{ {\hat B_{\theta '}}\} \). In these sets, θ and θ′ stand for the angular position, over a great circle of their respective single-qubit Bloch sphere, of the measurements performed by the daemons and θ, θ′ = 0 correspond to the z-axis. In a given run of the game, Aletheia measures operator \({\hat A_\theta }\) and communicates the corresponding outcome A θ to Bia, who attempts at evaluating the extractable work owing to the information gathered, locally, by Aletheia’s measurement. In fact, the latter allows Bia to reduce the entropy associated to her measurement result from the value H(B θ′) to H(B θ′|A θ ).24 With such information, using a Szilard-like machine, Bia would be able to extract an amount of work 1−H(B θ′|A θ ) from a hypothetical heat reservoir. An analogous reasoning can be carried out when exchanging the role of the daemons, concluding that, for a given setting, the extractable work per run of the game is

$${W_\rho }\left( {{A_\theta },{B_{\theta '}}} \right) = 1 - H\left( {{A_\theta },{B_{\theta '}}} \right) + \frac{1}{2}\left[ {H\left( {{A_\theta }} \right) + H\left( {{B_{\theta '}}} \right)} \right],$$
(1)

where H(A θ , B θ′) is the joint entropy of variables A θ and B θ′. For a sufficiently dense covering of the great circle, and for θ′ = θ, the average extractable work achieved through the game, maximized over all the possible great circles, is

\({\cal W}(\rho ) = \mathop {{\max }}\nolimits_\phi {\int}_0^{2\pi } {W_\rho }\left( {{A_\theta },{B_\theta }} \right)d\theta /2\pi \), where ϕ is the azimuthal angle for the great circles being considered. In ref. 25 it was shown that any separable state ρ is such that

$${\cal W}\left( \rho \right) \le {{\cal W}_f} = 0.443\,{\rm{bits}}.$$
(2)

where 𝒲 f is the maximum average work evaluated for any pure factorized state. Therefore, any surplus of extractable work above 𝒲 f arises in virtue of entanglement shared by the daemons. Equation (2) can then be used as a thermodynamically rooted entropic witness for inseparability.

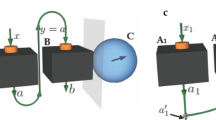
We employ the thermodynamics-based separability criterion in Eq. (2) for the characterization of photonic entanglement. As stated, our aim is to use information thermodynamics to assess entanglement, rather than replicating the behavior of a working medium in a photonic setup.26 Polarization-entangled pairs of qubits, ideally prepared in \(\left| \Phi \right\rangle = \cos \varphi \left| {HH} \right\rangle + \sin \varphi \left| {VV} \right\rangle \), are produced by using the double-pass source in ref. 31 (see Fig. 1a). Here, |H〉 (|V〉) stands for a photon in the horizontal (vertical) polarization state. Further, we explore how the thermodynamic bound evolves through a depolarizing channel (of strength 1−μ) degrading the initial state to the mixture \(\rho = \mu \left| \Phi \right\rangle \left\langle \Phi \right| + \left( {1 - \mu } \right){\Bbb I}/4\). This has been implemented by using two liquid crystals (LCs), with their axes at 0° and 45°, onto the path of one photon. The two crystals are tuned in such a way that they perform a rapid succession of Pauli operators \({{\it{\hat \sigma }}_x}\), \({{\it{\hat \sigma }}_{\it{y}}}\), \({{\it{\hat \sigma }}_{\it{z}}}\), thus generating white noise on the state.32, 33

Fig. 1
figure 1

a Experimental setup for the extractable work-based inseparability of bipartite states: The entangled photon source uses a 1.5-mm thick β Barium-Borate crystal pumped with 100 mW of laser at 355 nm, in conjunction with a spherical mirror (M), and delivers approximately 200 coincidence/s through 5 nm full width at half maximum interference filters. Details on the source can be found in ref. 31. We encode the logical states of each qubit in the horizontal and vertical polarization states |H〉 and |V〉 of each photon. Using quantum state tomography, we estimate a fidelity F = 0.961 ± 0.007 of the entangled resource with the maximally entangled state \(\frac{1}{{\sqrt 2 }}\) (|HH〉 + |VV〉). The corresponding value of tangle is T = 0.911 ± 0.008.34 The relative weight (\(\cos \varphi \)) of the two polarization contributions in such state can be tuned by the quarter waveplate (QWP m) in the source. One of the photons passes through a depolarizing channel, consisting of two LCs and the associated control electronics, which selects the value of μ. Finally, polarization measurements are performed at a polarization-analysis module consisting of a QWP, a HWP, a PBS, and an APD per mode. We also show the single-mode fibers used to convey the photonics signal to the polarization analysis module. Inset: measured W ρ (θ, θ) as a function of the measurement angle θ for state |ρ〉 with \(\cos \varphi = 0.85\), and μ = 0.98 (blue); \(\cos \varphi = 0.62\), and μ = 0.98 (purple); \(\cos \varphi = 0.62\), and μ = 0.51 (red). b Experimental setup for a GHZ-Cluster state. c Analogous setup for a W-type resource

Full size image

In the inset of Fig. 1a, we show typical experimental curves for the work W ρ (θ, θ) calculated according to Eq. (1), as we inspect the set of operator pairs used by Aletheia and Bia, labeled by the angle θ on the great circle of the Bloch sphere corresponding to the linear polarizations (i.e., the equator of the single-qubit Bloch sphere). This is the set of directions allowing for optimal work extraction (cf. “Methods”). The observed oscillations are due to the polarization unbalance, while the average level is affected by the purity of the state. For each choice of θ, we have calculated the Shannon entropy associated to single-particle operators, as well as the joint entropy associated to the joint operator. We have verified by numerical simulations that our covering with 19 different directions is sufficiently dense for the continuous approximation to hold. In addition, we have fully characterized our states with quantum state tomography, from which the maximal value of the Bell operator S has been extracted for a comparison with a standard entanglement witness.

We measured the extractable thermodynamic work for several sets of parameters φ and μ in the resource state, which were estimated by reconstructing the density matrix of the experimentally engineered state ρ exp via complete quantum state tomography for each position of the quarter waveplate (QWP) in the source (setting φ) and every configuration of the LCs (fixing μ). Extractable work has been calculated by measuring Shannon entropy spanned over the whole big circle of the Bloch Sphere.

In order to highlight the inherently different nature of the test implemented here and a standard Bell-CHSH test, we now consider the Bell function \(S = {\rm{T}}r[\rho ({\hat O_1} - {\hat O_2} + {\hat O_3} + {\hat O_4})]\) with \({\hat O_1} = {\sigma _x} \otimes {\sigma _x}(\alpha )\), \({\hat O_2} = {\sigma _x} \otimes {\sigma _z}(\alpha )\), \({\hat O_3} = {\sigma _z} \otimes {\sigma _x}(\alpha )\), and \({\hat O_4} = {\sigma _z} \otimes {\sigma _z}(\alpha )\). Here, \({\sigma _k}(\alpha ) = \hat R(\alpha ){\sigma _k}{\hat R^\dag }(\alpha )\) with \(\hat R(\alpha ) = (\cos \,\alpha) {\Bbb I} + (i\,\sin \,\alpha) {\sigma _y}\) and σ k is the k = x, y, z Pauli matrix. Local realistic theories bound such function as |S| ≤ 2, while quantum mechanically \(\left| S \right| \le 2\sqrt 2 \). Using state ρ, we find \(S = \mu [1 + \sin (2\varphi )][\cos (2\alpha ) + \sin (2\alpha )]\), which we have used to estimate the value of the Bell function using ρ exp for each set value of μ and φ.

The results of our experiment are summarized in Fig. 2, where we show the measured extractable work and the Bell function for two resource states with different values of φ. The comparison with Bell’s test reveals how both quantities capture the degradation resulting from the depolarization channel, and that they are similarly robust against the bias between the |HH〉 and |VV〉 contributions. A complete analysis shows that the relation between the thermodynamics-inspired criterion and Bell’s inequalities is not trivial. In fact, we were able to find values of μ and φ for which it is possible to violate just one of the two criteria, and vice versa. We have considered an experimental state with large bias (\(\cos \varphi = 0.25 \pm 0.03\)) and purity (μ = 0.97) that offers no violation of the local realistic bound (S = 1.977 ± 0.009). However, the corresponding extractable work is 𝒲 = 0.491 ± 0.021, which exceeds the separability threshold 𝒲 f by 2 standard deviations. This implies that the use of entanglement for powering a thermal machine is qualitatively different from that necessary for communication tasks, such as measurement-independent key distribution. These considerations are extended in the analysis reported in the Supplementary Information.

Fig. 2
figure 2

Experimental results for two different resource states corresponding to \(\cos \varphi = 0.62\) (a), and \(\cos \varphi = 0.85\) (b) for different strengths of the depolarizing channels μ. Red dots: experimental points for 𝒲 calculated from the experimental count rates measured in 30 s. Magenta dots: experimental points corresponding to the values taken by the Bell parameter, evaluated from the fully reconstructed state tomographies of the resource ρ exp. The value of \(\cos \varphi \) is evaluated by direct inspection of the coincidence rates, averaged over all the experimental states. The error bars take into account the Poissonian statistics of the measured rates and derived from direct error propagation for 𝒲 and Monte Carlo simulation for S. The green and blue dashed curves represent theoretical predictions based on state ρ, while the solid straight lines denote the entanglement thresholds and the Bell function. The dashed vertical lines identify the values of μ for which 𝒲 and S cross their respective bounds

Full size image

We now extend our investigation to the case of a tripartite system. It is well known that, for pure states, only two non-equivalent classes of genuine tripartite entanglement exist,35 either the GHZ or W class. Here, we focus on the ability of distinguishing GHZ-type entanglement from W-type one using a criterion inspired on thermodynamics rather than state fidelity.36 The protocol now involves a further daemon, Charis (Xάρις), which is set to act on her subsystem by acting in a way conditioned on information provided by Aletheia and Bia. The strategy they agreed on consists of the following steps: (a) Aletheia and Bia perform a projective measurement along a common axis u in the single-qubit Bloch sphere chosen among the three Pauli settings; (b) Charis receives information on the outcomes of such measurements. In light of such information, she can extract work from her system by performing a projective measurement along a suitably chosen direction v on the Bloch sphere; (c) In order to exclude bipartite entanglement and thus link the excess extractable work to the presence of genuine multipartite entanglement in our resource state, the protocol must be repeated by permuting the role of the three daemons (Fig. 3).

Fig. 3
figure 3

a–c Diagrammatic representation of the scheme extractable work-based tripartite inseparability. Each panel illustrates one of the steps of the protocol described in the main text

Full size image

Clearly, the amount of work that can be obtained in a single run of such a tripartite game is W ρ (A u , B u , C v ) = 1−H(C v |A u , B u ) with H(C v |A u , B u ) the Shannon entropy of variable C v conditioned on the outcomes A u and B u performed by Aletheia and Bia. A bound for the average extractable work, obtained by maximizing over the choice of v, can be established for separable states as:

$$\begin{array}{*{20}{l}}\\ {{\cal W}(\rho ) = \mathop {{\max }}\limits_v \,\frac{1}{3}\mathop {\sum}\limits_u {W_\rho }\left( {{A_u},{B_u},{C_v}} \right) \le {{\cal W}_f} = \frac{1}{3}.} \hfill \\ \end{array}$$
(3)

A violation of this bound signals the presence of entanglement in the state. Furthermore, it can be shown that W-type entanglement can only provide an extractable work of at most 7/9 = 0.778.25 Therefore, this thermodynamic criterion is well suited for identifying the entanglement class to which the state belongs: any extractable work in excess of 0.778 would signal GHZ character.

In order to achieve useful benchmarks for the performance of our experiments, we have performed a thorough theoretical analysis of the protocol for both pure and mixed-state resources. In particular, we have considered the achievable value of the extractable work 𝒲 when using the resource state \({\rho _3} = \mu \left| \Psi \right\rangle \left\langle \Psi \right| + \left( {1 - \mu } \right){\Bbb I}/8\) with |Ψ〉 a tripartite pure state. We have first focused on the case of μ = 1 with |Ψ〉 embodied by either a tripartite GHZ-Cluster state of the form:

$$\left| {GHZc} \right\rangle = \frac{1}{2}{\left( {\left| {000} \right\rangle - \left| {\left. {110} \right\rangle } \right. + \left| {011} \right\rangle + \left| {101} \right\rangle } \right)_{ABC}},$$
(4)

where {|0〉, |1〉} are the logical states of the three qubits, labeled as A, B, and C and owned by Aletheia, Bia, and Charis, respectively. This state can be shown to give rise to the same performance as a standard GHZ resource. The W-type resource is instead

$$\left| W \right\rangle = \frac{1}{{\sqrt 3 }}{\left( {\left| {001} \right\rangle + \left| {010} \right\rangle + \left| {100} \right\rangle } \right)_{ABC}}.$$
(5)

In Supplementary Information we have looked at the expected behavior of 𝒲 against the angular direction of the great circle on the single-qubit Bloch sphere identified by the angles (θ, ϕ), both for pure and mixed states.

Such predictions have then been tested in a two-photon implementation of both a three-qubit GHZ-Cluster-type state and a W-type one. Such states are generated by adding a path-encoded qubit to the two-qubit setup, as shown in Fig. 1b, c (cf. “Methods”). This arrangement allowed us to engineer both a GHZ-Cluster state of the form (|HH0〉 − |VV0〉 + |HV1〉 + |VH1〉) ABC /2 and a W-type resource state of the form \(\left| W \right\rangle = \left( {\left| {HH1} \right\rangle + \left| {HV0} \right\rangle + \left| {VH0} \right\rangle } \right)/\sqrt 3 \). Path-qubit analysis was performed by either selecting one of the two paths, which implements a projection in the computational basis, or selecting the proper phase shift ϕ between the two modes, thus enabling the projection on the diagonal basis (ϕ = 0, π) and the circular basis (ϕ = π/2, −π/2).

In all cases, there is a significant violation of the separability bound. Moreover, the symmetry among the results that we have achieved capture unambiguously the GHZ-Cluster character of the experimental resource. In order to show this feature more clearly, we have repeated the experiment when complete decoherence is introduced in one of the qubits of the system, in an attempt to render our resource state bi-separable and wash out its genuine tripartite entanglement. When full decoherence is introduced in the path-encoded qubit by inserting a thick glass plate on one of the paths, allowing to disrupt coherence between the two modes (independent of polarization), we get 𝒲1 = 0.799 ± 0.006. However, decoherence lessens the values of the other two witnesses, to values that are very close to the separability threshold in Eq. (3), demonstrating the disappearance of tripartite entanglement (Table 1).

Table 1 Extractable work in bits for the three permutations of roles in the protocol for extractable work-based inseparability evaluated using a GHZ-Cluster resource
Full size table

A similar analysis has been conducted using the experimental W-type resource, whose corresponding experimental results are reported in Table 2. As done for the GHZ-Cluster state, we have assessed both the case of a close-to-ideal resource and that of a strongly decohered one close to the separability threshold. The diversity (in terms of entanglement-sharing structure) of such resources is fully captured by the extractable work.

Table 2 Extractable work in bits for the three permutations of roles in the protocol for extractable work-based inseparability evaluated using a W resource
Full size table

A comparison with non-locality-based criteria similar to the one reported for the study of bipartite entanglement can be made in this tripartite context. Here, rather than concentrating on two-qubit correlations, we shall investigate their genuinely multipartite nature, whose characterization is clearly a much more demanding problem to tackle. A powerful tool in this respect is embodied by genuinely tripartite versions of a Bell inequality, such as the inequality proposed by Svetlichny,37 whose violation witnesses the occurrence of multipartite non-local correlations. Such inequality has been successfully experimentally violated using a photonic GHZ state38 and used to ascertain the properties of the ground state of a many-body system in a photonics quantum simulator.39

In the Svetlichny game, the daemons locally rotate their respective qubit by an angle α j (j = A, B, C) through the operator \(\hat {\cal R}({\alpha _j}) = (\cos {\alpha _j}){\sigma _z} + (\sin {\alpha _j}){\sigma _x}\) and project it over the basis of σ z . If state |0〉 (|1〉) is found, they attach a dicothomic variable the value +1(−1). This allows them to build the the statistical correlation function for local spin measurements E(α A , α B , α C ) and, in turn, construct the Mermin–Ardehali–Belisnskii–Klyshko function40, 41

$$ {M_3} = E({\alpha _A},{\alpha _B},{{\alpha '}_C}) + E({\alpha _A},{{\alpha '}_B},{\alpha _C})\\ + E({{\alpha '}_A},{\alpha _B},{\alpha _C}) - E({{\alpha '}_A},{{\alpha '}_B},{{\alpha '}_C}).$$
(6)

The Svetlichny function is thus S 3 = |M 3 + M′3|, where M′3 is the same as M 3 with α j  ↔ α′ j . Any biseparable state satisfies the inequality |S 3| ≤ 4. Tripartite entangles states violate the inequality up to the maximum value of \(4\sqrt 2 = 5.65685\), which is obtained using GHZ-like states. In fact, state |GHZc〉 allows to achieve such a maximum violation for (α A , θ B , θ C ) = (3π/8, −π/4, 0) and (α′ A , θ′ B , θ′ C ) = (π/8, 0, π/4). We have used the experimental quantum state tomographies of the GHZ-Cluster and W resource states to evaluate the Svetlichny function. After a global optimization over all the angles involved, we have found \(S_3^{GHZc} = 4.83 \pm 0.07\) and \(S_3^W = 3.39 \pm 0.06\). This shows that the experimental GHZ-Cluster state is consistently found to be entangled in a genuinely tripartite sense by both the extractable work-based criterion and the Svetlichny one. On the other hand, the non-locality-based entanglement criterion fails to detect the tripartite entangled nature of the experimental W resource, which is instead well captured by the sensitivity exhibited by the extractable work.

Discussion

We have demonstrated experimentally a fundamental result of information thermodynamics, showing that communication-assisted games based on Maxwell’s daemon are able to provide core information on the quantum correlated nature of the state of a multipartite system. Such protocols are both practical and fundamentally interesting in light of their distinct nature from, say, non-locality-based entanglement witnesses. This work has significant implications for both technological and conceptual aspects. Concerning the technological advances that it entails, the photonic platform we described has the capability of preparing, controlling and measuring, with high fidelity and a reduced experimental complexity, states of a multipartite working medium, addressing questions that are genuinely inspired by thermodynamic problems. General evolutions can be easily implemented or simulated, thus paving the way to the implementation of a fully fledged experimental assessment of non-equilibrium dynamics. The latter has so far been limited to either classical systems or nuclear magnetic resonance setups, where any quantum feature is weakened by the typically strong environmental actions. As for the fundamental aspects, we have highlighted how non-classical correlations within the working medium are strongly linked to the performance of thermodynamic processes, not differently from quantities with a counterpart in classical thermodynamics. This points to an interesting direction for understanding the emergence of ordinary world from its quantum microscopic constituents.

Methods

Two-qubit protocol

The bound on the extractable work is found by averaging over different projectctions by the daemons; these are performed by removing the QWPs from the polarization analysis module shown in Fig. 1, and using only the half waveplates (HWPs) to determine the direction of the projection. As we used two avalanche photo-diodes (APDs) after the polarizing beam splitters (PBSs), we had to implement four different types of measurements for each of the 19 choices of angular direction on the equator of the single-qubit Bloch sphere. In particular, we had to consider the four sets of directions (θ A , θ′ B ) = (θ, θ), (θ, θ +45°), (θ +45°, θ), (θ +45°, θ +45°), where the first (second) angular direction is for Aletheia’s (Bia’s) measurements choice. The corresponding detected coincidences at the APDs are labeled as \({N_{{\theta _A},\theta {\prime _B}}}\). A full circulation of the Bloch-sphere equator is then achieved by rotating the HWPs from 0° to 45° in 19 steps. This implies that a total of 76 measurements were needed in order to acquire the necessary information to reliably evaluate perform the performance of the scheme. Upon suitable normalization of the detected coincidence counts, we have the following set of probabilities:

$${p_{AB}}\left( \theta \right) = {N_{\theta ,\theta + 45^\circ }}/D\left( \theta \right),$$
(7)
$${p_A}\left( \theta \right) = ({N_{\theta ,\theta }} + {N_{\theta + 45^\circ ,\theta }})/D\left( \theta \right),$$
(8)
$${p_B}\left( \theta \right) = ({N_{\theta ,\theta }} + {N_{\theta ,\theta + 45^\circ }})/D\left( \theta \right)$$
(9)

with D(θ) = N θ, θ  + N θ, θ+45° + N θ+45°, θ  + N θ+45°, θ+45°. Example of measured coincidence counts are N 0, 0 = 3578, N 0, 45° = 58, N 45°, 0 = 173, N 45°, 45° = 4328, achieved in 30 s of measurement. These are instrumental to the evaluation of the Shannon entropies needed to calculate W ρ (θ, θ) and, in turn, 𝒲.

Three-qubit protocol

Our two-photon implementation of three-qubit states relies on the addition of a third qubit, encoded in the two paths within a Sagnac interferometer (consisting of a 50:50 BS and three mirrors) on one of the two photons; the logical state |0〉 correspond to the clockwise circulation of the photon inside the interferometer, and |1〉 to the anticlockwise circulation. The phase ϕ between such logical state can be tuned by tilting a thin glass plate, placed in one of the paths. This arrangement allowed us to engineer a GHZ-Cluster state of the form (|HH0〉 − |VV0〉 + |HV1〉 + |VH1〉) ABC /2 by introducing a HWP at 0° on the clockwise path |0〉 and a HWP at 45° on the anticlockwise one (cf. Fig. 1b). On the other hand, a W-type resource state of the form \(\left| W \right\rangle = \left( {\left| {HH1} \right\rangle + \left| {HV0} \right\rangle + \left| {VH0} \right\rangle } \right)/\sqrt 3 \) can be easily engineered by modifying the configuration for the GHZ-Cluster state. After changing the label of the two paths, a PBS can be added in the setup to perform a polarization-to-path mapping, and thus eliminate the contribution from state |VV1〉 (cf. Fig. 1c).