Introduction

Organometal halide (OMH) perovskites, such as methylammonium lead iodide (MAPbI3), have experienced an improvement of power conversion photovoltaic efficiency from 3.8% to a recent 22% in a rather short period of time.1,2 Moreover, their ease and low cost of processing and wide range of applications (e.g., solar cells, photodetectors,3,4,5,6,7 and lasing8,9,10,11,12), further explain why OMH perovskites are among the most currently investigated materials.

One important feature of OMH perovskites is the existence of domains and their possible effects on properties. Ferroelectric domains were first observed by piezoresponse force microscopy (PFM) in small MAPbI3 grains with typical size of 100 nm.13 Recently, crystallographic twin domains with sizes of 100–300 nm have been measured by transmission electron microscopy (TEM) in MAPbI3,14 and highly ordered domains15,16 with alternating polarization and a width of 90 nm were also detected by PFM. Furthermore, transport properties of ferroelectric domain walls were theoretically studied by Metropolis Monte-Carlo simulations,17 Landau–Ginzburg–Devonshire theory,18 drift-diffusion simulations,17,19 and nonequilibrium Green’s functions calculations,20 suggesting domain wall channels for efficient charge transport in OMH devices. Interestingly, OMH perovskites were also predicted to exhibit stable charged ferroelectric domain walls, in addition to the more common uncharged neutral ferroelectric boundaries.21,22,23 Charged domain walls can generate striking phenomena. For instance, based on first-principles calculations, Frost et al.22 propose that the existence of charged ferroelectric domain walls should lead to the separation of photoexcited electron and hole pairs. Liu et al.23 further calculated the atomic structure of charged domain walls and their stability, and suggested that they induce separate channels of electron–hole pairs, leading to reduced recombination losses. First-principles simulations also demonstrated that charged ferroelectric domain walls in OMH perovskites have rather different optical spectra than neutral ones21,24 in addition to having much smaller band-gaps,22,23 as a result of the associated built-in electric fields.

However, we are not aware of any comprehensive study investigating how the width of the ferroelectric domains, separated by a charged wall, affects energetics, structural, electronic and optical properties of OMH systems. It is, for instance, legitimate to wonder if increasing such width prevents the charged domain walls from being stable anymore, because more layers will be subjected to the energetically costly built-in electric fields. It is also worth studying if the enlargement of such width can allow a control of the electronic band gap. Can such enlargement even lead to an electronic band gap closing, that is, to an insulator-to-metal transition? In other words, is it possible to create a metallic wall in an insulating system by forming large enough ferroelectric domains in OMH perovskites, in analogy to what was found for some head-to-head (H-H) charged domain walls in typical ferroelectric perovskite oxides? Or, rather, do the charged walls in OMH perovskites remain insulating for any stable domain size, as analogous to what was reported in some tail-to-tail (T-T) charged walls in BaTiO3, ErMnO3 and (Ca, Sr)3Ti2O725,26,27,28,29?

Here, we show, by performing and analyzing first-principles calculations, that one particular type of charged ferroelectric wall in methylammonium lead iodide continues to be stable with a rather low domain wall energy for domain widths as large as 13 lattice constants, likely because of the small value of the component of the polarizations normal to the wall. Such domains are found to experience an internal depolarizing field whose magnitude is independent of the domain width, which results (i) in a linear decrease of the band gap from about ≃1.4 eV to about zero when the width increases up to 11 lattice constants; and (ii) in both the H-H and T-T domain walls becoming metallic for larger domain widths. Rather small charge transfer between these two domain walls is found in this latter metallic case.

Results

Monodomains

Let us first study polar monodomains of MAPbI3, and consider the dependence of their electrical polarization on the orientation of the methylammonium (MA) organic molecule. Here, we assume a cubic strain tensor for our lattice vectors (that is, we do not consider strain relaxation with respect to the cubic structure), as consistent with experiments30,31,32 and as also done in previous computational studies.12,33 We also adopt the experimental cubic lattice constant, that is, 6.31 Å.31,32 The polarization vector P is expressed here as (Px, Py, Pz), where Px, Py, and Pz are its components along the pseudocubic [100], [010], and [001] directions, respectively. We also define a vector θ, whose Cartesian components are the angles θx, θy, and θz that the C–N bond of the MA molecule makes with these three pseudo-cubic 〈100〉 directions, respectively. As consistent with the literature,34 we numerically find that two particular structures present the lowest energies among different polar phases of MAPbI3 monodomains: (1) one triclinic structure with P1 space group, which has a polarization equal to (4.2, 0, 12.7)μC/cm2 and a θ vector of (69.6°, 90°, 20.4°); and (2) a rhombohedral structure with R3m space group, with a polarization of (7.1, 7.1, 7.1)μC/cm2 and a θ vector equal to (54.7°, 54.7°, 54.7°). We will refer to these two structures as P[103] and R[111], respectively, where the uppercase letter is the first letter of the corresponding space group and with “[103]” and “[111]” referring to the crystallographic pseudo-cubic direction along which the polarization essentially lies. Note that the P[103] structure is energetically lower by 21 meV per formula unit than R[111] in our calculations, as consistent with ref. 34

Structure of multidomains

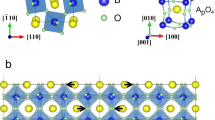
We now consider multidomains configurations in which one initial domain is in a P[103] or R[111] configuration while the other initial domain is in a different P[103] or R[111] configuration, with the polarization difference along the normal of the domain wall (ΔPn) between these two initial configurations being finite. In other words, we consider charged domain walls. The only charged wall that is found to be stable in our relaxed simulations (using 10 × 1 × 1 supercells) corresponds to one domain having a polarization lying close to the pseudo-cubic [103] direction and the second domain possessing a polarization being nearly parallel to the [−103] direction. This multidomain is denoted here as P[103]&P[−103] and is shown in Fig. 1 for a 10 × 1 × 1 supercell. It possesses the smallest ΔPn (namely about 8 μC/cm2) among all the initial ones we presently considered. All the other investigated charged walls with larger ΔPn undergo polarization changes in the domains when relaxing the structure within our computations, which contrasts with results from earlier calculations23 and therefore makes us wondered if these previous simulations were fully converged.

Fig. 1
figure 1

Example of a P[103]&P[−103] multidomain structure in MAPbI3. The supercell chosen here is 10 × 1 × 1

Full size image

Domain wall energy of multidomains

Let us now investigate the effect of the domain width on energetics and properties of the stable P[103]&P[−103] multidomain. For that, we consider n × 1 × 1 supercells, where n is even number ranging from 2 to 26, inside which there is a domain of width equal to n/2 in lattice constant units in the initial configuration P[103], alternating along the x-axis with a domain of the same width in the P[−103] initial state. The domain wall energy is calculated as:23

$$E_{DW} = \frac{{E_{MD} - E_{SD}}}{{2S_{DW}}},$$
(1)

where EMD is the energy of the P[103]&P[−103] multidomain as computed in the n × 1 × 1 supercell, ESD is the energy of the single P[103] domain within the same supercell, and SDW is the area of domain wall. As shown in Fig. 2a, EDW increases with the domain width when increasing n from 2 to 22, and then appears to saturate for n larger or equal to 22. At this saturation and for n = 26, EDW is equal to 46 mJ/m2, which is comparable to the 35 mJ/m2 value for the 90° neutral domain wall and the 132mJ/m2 result for the 180° neutral domain wall in inorganic ferroelectric PbTiO3.35 The low domain wall energies shown in Fig. 2a, therefore strongly suggest that our considered charged domain walls are all energetically feasible in MAPbI3, which is therefore promising for engineering domains of different width. Such low values likely result from the aforementioned small magnitude of ΔPn. Note also that the presently predicted EDW for the 6 × 1 × 1 supercell is about twice smaller than the one provided in an earlier study,23 which may originate from the use of a less dense Monkhorst–Pack k-point grid in that previous work.

Fig. 2
figure 2

Domain wall energy a and electronic band gap b as a function of the integer n defining the width of the P[103]&P[−103] domain structures of MAPbI3

Full size image

Electronic band gap of multidomains

Furthermore, Fig. 2b reports the behavior of the electronic band gap as a function of n in the whole P[103]&P[−103] multidomain (that is, for the domains and walls). Such band gap nearly linearly decreases from 1.41 eV to zero when n increases from 2 to 22. The system then undergoes an insulator-to-metal transition for n around 22, and the walls remains metallic for larger domain widths. Let us first indicate that the electronic band gap of the P[103] monodomain is numerically found to be equal to 1.45 eV, which agrees rather well with the measured values of about 1.5–1.6 eV1,31 as well as with the corresponding band gap of about 1.67 eV obtained from accurate fully self-consistent GW calculations incorporating spin–orbit coupling.21 As a result, it appears that we can rather safely trust the values of the band gap displayed in Fig. 2b, which also tell us that an efficient band-gap engineering by around 1.4 eV in variation can be accomplished by playing with the width of domains with charged walls in MAPbI3. Interestingly, the linear decrease in electronic band gap with the domain width (when n varies from 2 to 22), as well as the metallic character for n ≥ 22, displayed in Fig. 2b automatically imply that the electrical conductivity should be enhanced as the domains widen. Moreover, Fig. 3 reveals that the optical band gap of the studied multidomains is basically independent of the domain width, and equal to about 1.5-1.6 eV. One can then imagine different device applications, exploiting the tuning of the electronic band gap by the domain width and/or the fact that optimal optical band gaps for solar conversion efficiency are of the order of 1.1–1.6 eV36—that is within the range of our computed optical band gap (note also that photovoltaic applications depend on both the optical and electronic band gaps36).

Fig. 3
figure 3

Tauc plot for bulk of MAPbI3 and P[103]&P[−103] multidomains corresponding to the supercells n × 1 × 1, where n = 2, 8, 14, and 22. Their optical band gap of multidomains are all in the range of 1.5–1.6 eV, and is therefore very close to that of the bulk (which is presently computed to be 1.59 eV)

Full size image

Discussion

Let us now try to understand the aforementioned behavior of EDW and of the band gap as a function of n. For that, Fig. 4a displays cos(φx), where φx is the angle made by the C–N bond with respect to the x-axis (as shown in Fig. 1 for some cells), versus the cell index along this x-direction. Note that cos(φx) is numerically found to be directly proportional to the x-component of the polarization in the monodomain case. In particular a change of sign of cos(φx) reflects a change of sign of this Px. Interestingly, the magnitude of cos(φx) in the middle of both domains for any considered n is close to that in the monodomain, that is cos(69.6°) = 0.35, implying that the domains possess a x-component of polarization similar to that of the monodomain. Figure 4a further reveals that cos(φx) experiences jumps and changes of sign at the H-H and T-T domain walls, while in the middle of the P[103]&P[−103] domains we obtain values that are close to their monodomain counterpart (about 69.6°). Note that for n, larger than 14, there are noticeable fluctuations of cos(φx) within the P[103]&P[−103] domains, which may explain the change of slope of the EDW curve in Fig. 2a at n ≈ 14. It is also informative to point out that such different dependency occurs at the width of n = 14 for which the electronic band gap is about half of that of the monodomain case (see Fig. 2b). Interestingly, the values of cos(φx) just before and just after the two aforementioned jumps at the domain walls are nearly independent of n. As a result, the positive (respectively, negative) ΔPn at the H-H (respectively, T-T) domains is basically the same for any considered domain width. The resulting bound charges at the domain walls can be computed as minus the product of ΔPn and the SDW area, and are found to be equal to about 0.19e in magnitude for any studied domain. In contrast, the free charges, which can be estimated by integrating the density of states across the Fermi level, are basically null for n<22 and as small as 0.01e, 0.012e, and 0.013e for n = 22, 24, and 26, respectively. As a result, the internal depolarizing electric field almost fully arises from bound charges in our studied domains walls, implying it should remain essentially constant within that range of investigated domain widths (on the other hand, the slightly aforementioned enhanced value of the free charges when n is increased above 22 strongly suggests that such internal depolarizing field would be reduced in magnitude for much larger n than those studied here). To check the assumption of depolarizing electric field being independent of our considered domain widths, Fig. 4b shows the electrostatic potential within the domains for widths n = 10, 18, 22, and 26. One can see that the slopes of this electrostatic potential are very similar for these different n, including that of n = 22 and n = 26 (that are metallic cases). As a result, a similar electric field indeed exists inside all our studied domain structures. The fact that such depolarizing field is independent of n can be understood by a simple model based on the parallel two-plate capacitor. As a matter of fact, such capacitor possesses an internal electric field that lies along the normal of the plates and with a magnitude given by

$$E_{in} = \frac{\sigma }{\varepsilon },$$
(2)

where σ is the charge density on the parallel plates and ε is the dielectric constant of the inside medium. In our case, as free charges are negligible, the two-dimensional charges are mainly the bound charges occurring at the H-H and T-T domain walls (that are independent of n, as suggested by Fig. 4a, b) and the dielectric constant can be thought to be that of the MAPbI3 monodomain. The existence of an internal electric field that is independent of the domain width can explain several important features of Fig. 2. For instance, EDW becomes larger with the domain width (see Fig. 2a), simply because more and more layers feel such energetically costly identical depolarizing field when increasing n. Under the influence of this same internal electric field, the energy of the valence band maximum should linearly increase with the domain width while that of the conduction band minimum should linearly decrease, since the difference in electrostatic potential between the T-T and H-H domain walls is directly proportional to the product between this electric field and n. Such field-induced behavior therefore provides a natural explanation of why the band gap is linearly reduced to zero when n is enhanced up to n = 22, and why the studied systems becomes metallic for domains with larger width (see Fig. 2b).

Fig. 4
figure 4

Structural and electric properties of P[103]&P[−103] domain structures of MAPbI3. a displays cos(φx) (see text and Fig. 1) as a function of the cell index along the x-axis for some specific n × 1 × 1 supercells. b shows the electrostatic potential within the domains having charged walls and associated with n = 10, 18, 22, and 26. The drop of the lines in both panels indicate periodicity of the considered supercell

Full size image

To confirm such hypotheses, Fig. 5a–c reports the computed layer-resolved local density of states for n = 10, n = 18 (both insulator cases), and n = 22 (metallic situation), respectively. In the insulating cases, the valence band maximum occurs at the T-T domain walls while the conduction band minimum is located at the H-H domain walls. Note that such depolarizing-field-induced difference in location between the conduction band minimum and valence band maximum was already pointed out in ref. 23. As also indicated in that reference, this may provide a mechanism for the spatial separation of electrons and holes, and their delayed recombination, which is of obvious interest in the context of photovoltaic and optoelectronic applications. When setting the energy of the valence band maximum to be the zero of energy in the insulating cases (this zero in energy also coincides with the Fermi level in that situation), it is indeed found, by, e.g., comparing Fig. 5a, b, that the conduction band energy decreases when increasing the domain width up to n = 22. Comparing Fig. 5a, b with Fig. 5c also indicates that some states that belonged to the valence band in the T-T domain walls for n lower than 22 are above the Fermi level for n equal or larger than 22, therefore demonstrating that the T-T walls are now metallic. Similarly, some states that were at the bottom of the conduction band in the H-H walls in the insulator situation (see Fig. 5a, b) are located below the Fermi level in the metallic case (see Fig. 5c), characterizing the metallization of the H-H walls. Note, however, that the number of such states located just above (respectively, below) the Fermi level in the metallic case in the T-T (respectively, H-H) domain walls is rather small. In fact, integrating the local densities of such states provides a charge of less than 0.02e of magnitude, therefore indicating that the transfer of charges between the T-T and H-H domains is tiny even when the system becomes metallic—which also explains why the depolarizing field remains essentially constant even after metallization of the charged walls for n>22 (as evidenced in Fig. 5b). Furthermore, Fig. 5d depicts the band structure for n = 22, which shows that, in terms of k-points, the crossing between valence and conduction states at the Fermi level occurs near the R-point located at q = (π/a, π/b, π/c), where a–c are the lattice constants of the 22 × 1 × 1 supercell.

Fig. 5
figure 5

Electronic properties of P[103]&P[−103] domain structures of MAPbI3. a–c report the layer-resolved local density of states for the 10 × 1 × 1, 18 × 1 × 1, and 22 × 1 × 1 configurations, respectively, when going from the T-T (top figure) to H-H (bottom figure) layers. d shows the energy band structure for the n = 22 case. Note that the numbers “−5”,.. “0” indicated in a correspond to the layers shown in Fig. 1, and a similar nomenclature is used for b and c. The vertical dashed lines in a–c represent the energy of the Fermi level (which is chosen to be the zero in energy)

Full size image

In summary, we use first-principles calculations to investigate the energetics, as well as the structural and electronic properties of domains with charged walls in MAPbI3, as a function of the width n of these domains. It is found that these walls all have a rather low energy, which is promising to experimentally observe all of them—especially, when realizing that some schemes exist (e.g., applying electric fields of different magnitudes during frustrative poling procedure37 to create domains, having charged walls, with different size). Furthermore, increasing the domain width up to n = 22 unit cells induces a linear decrease of the electronic band gap from ≃1.4 eV to zero, as a result of a built-in depolarization electric field that is basically independent of our studied n domain widths and which therefore leads to an efficient band-gap engineering [let us also reiterate that the (electronic) band gap shown in Fig. 2b is the calculated one between the conduction band minimum (CBM) and valence band maximum (VBM) of the whole system, and that such VBM and CBM states do not have to be located at the same layer. On the other hand, the local electronic band gap from a valence state to a conduction state associated with the same layers is basically similar for any layer and any studied domain width for n below 22 (see Fig. 5a–c). As a result, the narrowing of the electronic band gap of the whole system can be thought to result from band bending, especially since the optical band gap shown in Fig. 3 is basically independent of n and equal to about 1.5 eV]. Furthermore, such electric field further results in an insulator-to-metal transition at both T-T and H-H walls for n exceeding 22 unit cells. Note also that this built-in internal electric field originates from the fact that the H-H domain walls are positively charged while the T-T domain walls are negatively charged. As a result, the internal electric field is aligned along our x-axis, implying that it should be easier for electrons and holes to move (parallel or antiparallel) along such axis than perpendicular to it. In particular, the photogenerated electrons will move towards the H-H domain walls while the photogenerated holes will move towards the T-T domain walls. We thus hope that the present study will not only deepen our current knowledge of ferroelectrics, photovoltaic materials, domain walls and optical phenomena, but will also encourage experimentalists to confirm our present predictions.

Methods

Density-functional calculations within the generalized-gradient-approximation are conducted, using the Vienna ab initio simulation package.38,39 The PBEsol functional is employed,40 along with a set of projector-augmented wave potentials to describe the electron–core interaction. An energy cutoff of 550 eV is also used. Electronic relaxations are taken to be converged within 10−6eV and ionic relaxation is performed until the residual force is less than 0.01 eV/Å on any ion. We use a 8 × 8 × 8 Monkhorst–Pack k-point grid for the 12 atoms unit cell of MAPbI3 and the k-meshes for larger supercells (including domain walls) are chosen accordingly to render the same k-point density as for the unit cell. Moreover, the polarization is calculated by the Berry phase method.41 Note that spin–orbit couplings and rotations of the PbI6 octahedra are neglected here. The electronic band gap of the MAPbI3 bulk (P[103] monodomain) is numerically calculated to be equal to 1.45 eV, which agrees rather well with the measured values of about 1.5–1.6 eV1,31 as well as with the corresponding band gap of about 1.67 eV obtained from accurate fully self-consistent GW calculations incorporating spin–orbit coupling.21 Such comparisons testify of the accuracy of the computational approach we presently use.