Introduction

Thermodynamic equations of state (EOS) for crystalline solids describe material behaviors under changes in pressure, volume, entropy and temperature; making them fundamental to scientific research in a wide range of fields, including geophysics, energy storage and development of novel materials.1,2,3 Despite over a century of theoretical development and experimental testing of EOS for solids,4,5 there is still a lack of consensus on the most appropriate EOS under various conditions or even the metric to evaluate appropriateness. Previous attempts6,7 have focused on comparison with the experimental data, which limits the range of the accessible data. By contrast, computational studies can span chemical and structural space in a consistent and methodical manner, and are often able to probe extreme conditions beyond the range of current experimental techniques. Density-functional theory (DFT) is gaining grounds as a first principles methodology that can accurately and efficiently search material space for complex functionality. In well-characterized systems, DFT calculations have been shown to be precise and reliable.8 In particular, Lajaeghere et al. recently benchmarked results for DFT-calculated thermodynamic properties of the elements, and found overall satisfactory agreement between prediction and experiment (excepting cases where magnetic, correlative, or relativistic effects are significant; or in cases where van der Waals forces are dominant).9 While direct calculations of systems under pressure are possible in most DFT codes, the equations of state provide a simple mathematical handle with minimum computational cost. These considerations pave the way for high-throughput studies that probe extreme conditions using DFT generated EOS.

There are three key questions to answer in order to utilize high-throughput DFT-based EOS. Which EOS best encapsulates the fundamental physics presented by DFT and are there rules or metrics that define EOS applicability? Are the optimal DFT-based EOS consistent with experimental values, and are therefore likely to reflect our physical reality? What are the limitations of these EOS?

Results and discussions

Equations of state

The equations investigated in this study are described in detail below, and summarized in Table 1.

Table 1 Theoretical isothermal EOS investigated in this study
Full size table

Birch (Euler and Lagrange)

Both forms of the Birch equation were derived by Francis Birch in 1947 for crystalline solids of cubic symmetry.10 The derivation was based on Francis Murnaghan’s extensive tensor formalism for analyzing finite strains.11 The first Birch equation uses the Eulerian strain metric; the second form is based on the Lagrangian metric (roughly the inverse of the Eulerian). As noted by both Birch and Murnaghan, the Eulerian metric is generally considered to be a more apt description of elastic behavior for non-infinitesimal strains, since it treats the final (rather than initial) coordinates as the independent variable. The energy–volume relation arising from the Eulerian viewpoint is:

$$E = E_o + BV_o\left( {\left( {\nu ^{ - \frac{2}{3}} - 1} \right)^2 + \frac{C}{2}\left( {\nu ^{ - \frac{2}{3}} - 1} \right)^3} \right),$$
(1)

where \(\nu \equiv \frac{V}{{V_o}}\), and Eo and Vo are the calculated equilibrium energy and volume, respectively, at zero pressure and absolute zero temperature. As for all subsequent formulations, the values of bulk modulus (K) and its pressure derivative (K′) at ν = 1 may be expressed in terms of the fitting parameters B and C:

$$K = \frac{{8B}}{9}$$
(2)
$$K\prime = C + 4$$
(3)

Birch’s equation from the Lagrangian viewpoint is:

$$E = E_o + BV_oC - BV_o\nu ^{\frac{2}{3}}\left( {(C - 2)\left( {1 - \nu ^{\frac{2}{3}}} \right)^2 + C\left( {1 - \nu ^{\frac{2}{3}}} \right) + C} \right),$$
(4)

where:

$$K = \frac{{16B}}{9}$$
(5)
$$K\prime = C - 2$$
(6)

Mie–Gruneisen

The Mie–Gruneisen EOS is based on the well-established empirical form of a general interatomic potential:4,5

$$E = \alpha r^m + \beta r^n$$
(7)

Setting m = −1 gives a reasonable representation of the Coulombic interaction between two atoms;12 under the restriction that E = Eo at r = ro reduces the four parameters in Eq. (7) to two to give:

$$E = E_o + \frac{{BV_o}}{C} - \frac{{BV_o}}{{C - 1}}\left( {\nu ^{ - \frac{1}{3}} - \frac{1}{C}\nu ^{ - \frac{C}{3}}} \right),$$
(8)

where:

$$K = \frac{B}{9}$$
(9)
$$K\prime = \frac{{7 + C}}{3}$$
(10)

Murnaghan

Interestingly, the Murnaghan equation is based not on Francis Murnaghan’s prodigious 1937 paper, but rather on a short communication from 1944 in which he proposed a relatively simple EOS based on a linear variation of the bulk modulus with respect to pressure.13 This hypothesis leads to the equation:

$$E = E_o + \frac{{BV_o}}{{(C + 1)}}\left( {\frac{{\nu ^{ - C} - 1}}{C} + \nu - 1} \right),$$
(11)

where:

$$K = B$$
(12)
$$K\prime = C + 1$$
(13)

Pack–Evans–James

Pack et al. posited an exponential variation of pressure with respect to changes in volume (based on quantum mechanics), and adjusted their expression to ensure proper limiting behavior as pressure approaches zero or infinity:14

$$E = E_o + \frac{{BV_o}}{C}\left( {\frac{1}{C}\left( {e^{3C(1 - \nu ^{\frac{1}{3}})} - 1} \right) - 3\left( {1 - \nu ^{\frac{1}{3}}} \right)} \right),$$
(14)

where:

$$K = B$$
(15)
$$K\prime = C + 1$$
(16)

Poirier–Tarantola

Poirier and Tarantola proposed that pressure is best expressed in terms of a logarithmic strain metric (as opposed to the Eulerian or Lagrangian metrics of Birch’s equations).15 The resulting energy–volume relationship is:

$$E = E_o + BV_o\left( {{\rm{ln}}(\nu )} \right)^2\left( {3 - C\left( {{\rm{ln}}(\nu )} \right)} \right),$$
(17)

where:

$$K = 6B$$
(18)
$$K\prime = C + 2$$
(19)

Tait

The Tait equation was developed nearly 150 years ago based entirely on the empirical observations of Peter Tait, who was investigating the compressibility of seawater, and modified a few decades later by Gustav Tammann from a linear average to a differential form,16 leading to the relation:

$$E = E_o + \frac{{BV_o}}{C}\left( {\nu - 1 + \frac{1}{C}\left( {e^{C(1 - \nu )} - 1} \right)} \right),$$
(20)

where:

$$K = B$$
(21)
$$K\prime = C - 1$$
(22)

Vinet

The Vinet equation was shown by Stacey to be equivalent in formulation to the Rydberg potential:7,17

$$E = D(ar + 1)e^{ - ar}$$
(23)

This leads to the following energy–volume equation:18

$$E = E_o + \frac{{BV_o}}{{C^2}}\left( {1 - \left( {1 + C\left( {\nu ^{\frac{1}{3}} - 1} \right)} \right)e^{C\left( {1 - \nu ^{\frac{1}{3}}} \right)}} \right),$$
(24)

where:

$$K = \frac{B}{9}$$
(25)
$$K\prime = \frac{{2C}}{3} + 1$$
(26)

The Jellium EOS,19 a third-order polynomial fit to energies, has historically shown a high quality of fit when utilized with the DFT data.8 The authors for this EOS motivate their equation (which is essentially a polynomial expansion in powers of \(x \equiv \left( {\frac{V}{{V_0}}} \right)^{ - 1/3}\)) by arguing that each power of x corresponds to a contribution to the energy of a crystal structure as a function of its cell volume. However, it does not appear that these justifications are entirely physical. For example, the x2 term in the Jellium model is aimed to represent the kinetic energy of an electron gas surrounding the atoms in the crystal. However, if the total energy varies roughly in proportion to \(\left( {\frac{V}{{V_0}}} \right)^2 - \left( {\frac{V}{{V_0}}} \right)\) (as is the case with NaCl, for instance), this coefficient is almost certainly negative if one examines the Taylor expansion of E as a function of x. Hence, as the Jellium EOS may in some cases revert to a non-physical polynomial function, we did not include it in this study.

Optimal equation of state

Metrics and correlations were derived from the equation of state and data compiled in the Materials Project. The relative root mean square deviation (RMSrD) was used as the primary metric for quality of fit, defined as:20

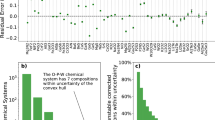
$${\rm{RMSrD}} = \sqrt {\frac{{\mathop {\sum}\limits_{i = 1}^N \left( {\frac{{E_i^{DFT} - E_i^{FIT}}}{{E_i^{DFT}}}} \right)^2}}{{N - 1}}} .$$
(27)

The RMSrD values for the fits of all EOS across the investigated material set are shown for the elements (Fig. 1) (see Supplementary Fig. S1 in SI for data on the compound set). Noble gases have been excluded from the elemental set due to drastic deviations from ideal behavior for solids: in the most extreme case, oscillations in the E–V curve of Kr lead to an RMSrD of 37%, orders of magnitude larger than the mean values in Fig. 2. Other studies have shown that it is necessary to incorporate the effects of van der Waals forces in the calculations to adequately capture the energy curve behavior of noble gases,21 however, these forces were not included in our simulations. There is an interesting periodic trend in the plot of Fig. 1, which indicates a correlation between error in EOS fit and number of valence electrons for a given element. We conjecture that this is due to the inability of the simplified EOS models to capture the physics of systems with greater numbers of interacting bodies (the implicit assumption being that DFT is able to do so more accurately, although previous comparison to experimental data has demonstrated that this method is likely still prone to some error.9) It is clear from this plot that the Lagrangian formulation of the Birch EOS (Eq. (5)) fares significantly worse than the other EOS under consideration and for this reason, it has been removed from subsequent plots in order not to obscure other data. This property has been remarked by previous authors,6,10 however, we do not believe any physical interpretation has previously been offered. We therefore point out that in approximately harmonic systems, where the E–V curve is dominated by a quadratic strain term, the Eulerian metric more closely resembles the true E–V relation for most solids (Fig. 3). This observation might be taken into consideration for future theoretical work.

Fig. 1
figure 1

RMSrD values for theoretical EOS fitted to DFT calculations of the elements

Full size image
Fig. 2
figure 2

Violin plots showing distribution of RMSrD values for each EOS across the combined set of elements and compounds

Full size image
Fig. 3
figure 3

Plot of the squared strain metrics ηEul and ηLag, which are the bases for Eqs. (1) and (4), respectively. Note that the graph of \(\eta _{Eul}^2\) more closely resembles a physical E–V relation for a solid with positive coefficient of linear expansion

Full size image

There is a large degree of variability in RMSrD from material to material, captured by the violin plot in Fig. 2 which displays the distribution for the combined set of elemental and compound materials. The average relative deviations are less than 1% regardless of material or theoretical equation used to fit the E–V data for most materials investigated, which suggests that for general purposes of approximation, the particular choice of EOS is not crucial. Because the mean RMSrD values for some of the equations were quite close to each other, we also compared EOS performance on the basis of a few other error metrics: maximum relative deviation (MrD), the greatest magnitude of fractional deviation for a given fitted E–V curve from DFT-calculated points; statistical uncertainty for each of the fit parameters (E0, V0, K, K′) as calculated from the least-squares. These analyses do not indicate a clearly superior EOS (see for example, Supplementary Fig. S2 in the SI), however, do suggest that the Birch (Eulerian), Tait, and Vinet equations tend to show lower deviation from calculated data points and less variability of fitting parameters than the other equations investigated.

The RMSrD values did not exhibit strong correlation with the bulk modulus or the band gap in the elemental and compound sets (see Supplementary Tables S1 and S2 and Supplementary Figs. S3 and S4 in SI). This suggests that neither the metallic/insulating nature nor softness of the material are predictive of error in the fitted EOS. The effect of structure within a fixed chemical system was also investigated for several materials, examples of which are shown in Figs. 4 and 5 for various polymorphs of Al2O3 and Ga, respectively. Al2O3 shows essentially no variation of quality of fit for any equation across a range of crystal systems. This is especially notable in light of the fact that both forms of the Birch equation were derived for media of cubic symmetry,10 with the rest assuming an isotropic medium. In contrast, Ga does exhibit noticeable variation in RMSrD between different polymorphs. Similar trends were observed for other chemical systems, with stiff metal oxides exhibiting low variability relative to softer metals (see Supplementary Figures S5 and S6 in SI). It is true that structures with different space groups may still have similar physical properties; this typically occurs when one structure is a slight distortion of another with higher symmetry. We examined the supergroup/subgroup relations of the given systems, and did not find this to be the determining factor in the similarity or difference in error trends. For example, the only relation of this type in the alumina polymorph set (besides the trivial P1, which is a subgroup of every space group) is P21/c and C2/m (numbers 14 and 12, respectively); whereas for gallium, Cmce (number 64) is a subgroup of Cmcm (number 63) and I4/mmm (number 139). These findings suggest that variations in structure are not necessarily predictive of variations in error for fitted EOS.

Fig. 4
figure 4

RMSrD values for theoretical EOS fitted to DFT calculations of various polymorphs of Al2O3

Full size image
Fig. 5
figure 5

RMSrD values for theoretical EOS fitted to DFT calculations of various polymorphs of Ga

Full size image

Benchmarking to Experiment

Given the overall quality of performance of the Birch (Eulerian), Tait, and Vinet equations, these were selected further benchmarking analysis. To verify the ability of DFT-based EOS to predict experimentally observed behavior, we compared the values of the bulk modulus (K) derived from the EOS for each material with values found in the literature. All three equations yielded similar results as determined by the mean unsigned percent error between calculation and experiment, which was in every case about 18% for the elemental set and 12% for the compound set. Results are shown in Figs. 6 and 7 for the Vinet equation, which had the smallest overall average error (by less than one percent). Similar plots for the other two EOS are provided in Supplementary Figs. S8–S11 of SI. There is limited experimental data on second-order elastic constants (used to calculate K′), but a few systems are compared in Fig. 8.

Fig. 6
figure 6

Comparison of experimental and calculated values of bulk moduli (K) for elements and compounds (using the Vinet EOS, Eq. (24) to derive K). Dashed lines show least-squares linear regression. References for experimental bulk modulus values are given in Supplementary Tables S3 and S4 of SI

Full size image
Fig. 7
figure 7

Comparison of EOS- and elastic tensor-derived values of bulk moduli (K) for elements and compounds (using the Vinet EOS, Eq. (24) to derive K). Dashed lines show least-squares linear regression

Full size image
Fig. 8
figure 8

Comparison of experimental and calculated values of bulk modulus pressure derivatives (K′). Gray bar denotes range of experimental values cited for NaCl,1,42 Fe,14,43,44 Ge,43,45 Mo,41,43,44 and Pb14,43,44

Full size image

Agreement between experimental and calculated values of elemental and compound bulk moduli is good, with regression slope and R2 values for both sets very close to 1 (Fig. 6). Previous studies have indicated that zero-point energy can lead to greater discrepancy between 0 K calculations and experiment for lighter elements,22 however, the error in bulk modulus values was not correlated to atomic mass for the elemental data set in this study (see Supplementary Figure S7). A few elements show variation from experimental data of greater than 50 GPa, labeled on the figure. Of these, Cr, Np, and Pa have been studied elsewhere by both experiment and calculation, and have shown similar systematic deviations as reported here. The discrepancy for Cr arises from magnetic ordering,23 which was not considered in this study. Previous experimental studies have shown that the bulk modulus of this element increases considerably at lower temperatures (nearly 20% from room temperature to 77 K).24 The variations for Np and Pa have been attributed to bonding in 5f orbitals.25,26 Previous studies using exact and overlapping muffin tin orbitals have been able to reproduce experimental elastic properties of actinides, in particular plutonium.27 This all-electron DFT method, while effective, is computationally expensive and difficult to generalize, making it unsuitable for EOS generation in high-throughput schemes.

Comparison to experimental values of K′ is more difficult, since they are small dimensionless quantities (typically in the range of 1–10), and the combination of experimental uncertainties and inherent variability due to different methods of fitting data lead to a wide range of cited literature values even for a single material. Figure 8 shows a few representative examples. Since the bulk modulus pressure derivative can be used to derive other material properties, such as behavior at finite temperatures,7 it is useful to have an internally consistent method for deriving K′ (although it should be noted that, since K′ is the highest-order fit parameter for the EOS investigated here, it is subject to the largest statistical uncertainty; see Fig. 9e). In light of their demonstrated accuracy in predicting K values, we therefore propose that numerically-derived EOS are valid avenues for analyzing and predicting thermodynamic properties of solid crystalline materials.

Fig. 9
figure 9

Violin plots showing distribution for each EOS across the combined set of elements and compounds of MrD (a) and statistical uncertainty of the fit parameters E0 (b), V0 (c), K (d), and K′ (e)

Full size image

Bulk moduli calculated from the EOS were also compared against bulk moduli calculated from the elastic tensor using the formation detailed in elastic tensor workflow for Materials Project.28 For the most part, values are identical, with some elements showing noticeably lower values from the elastic tensor workflow (Fig. 7). This is likely due to higher order terms the E–V curves, or asymmetries of the unit cell (e.g., in the cases of Tb and Dy). The discrepancy in carbon is due to the nature of the ground state structure, which is layered (graphite). This leads to a highly anisotropic elastic tensor, and the Voigt-Reuss-Hill averaging scheme is skewed by the low shear modulus of this structure.28 On the other hand, the shear modulus is not accounted for by the isotropic volumetric deformations employed in this study resulting in a far less significant effect of the lack of inter-layer cohesive forces on the calculated bulk modulus.

Since many applications for thermodynamic EOS involve materials subjected to extreme pressures (e.g., in geophysical research,29) it is natural to inquire whether there are pressure limits beyond which the DFT-derived EOS are no longer valid. A rough measure of these limits is given by comparing the maximal value found in the literature for pressure exerted on a material to that reached by the DFT simulation. Our findings, listed in Supplementary Tables S5 and S6 in SI, indicate that in many cases (e.g., AgCl), the latter of these limits is greater than or equal to the former, so that no extrapolation of the EOS is necessary for comparison with experimental results. However, in some cases, extrapolation would still be necessary: for example, for BeO, a stiff ceramic material, the maximum calculated volumetric compression of 15.7% corresponds to a calculated pressure of 127.5 GPa, whereas pressures of up to 175 GPa have been achieved in laboratory settings30 (see Supplementary Table S5 in SI). Because computations are capable of pressurizing a material well beyond the validity of the pseudopotential approximation, extrapolation of the EOS may in some cases give a more physically valid (and computationally cheaper) prediction than simply performing higher-pressure calculations.

Many of the materials exhibit phase transformations far below the pressure range of the DFT curves, in which case the question is no longer whether a single DFT-derived EOS is valid at high pressures, but whether we can use DFT-based EOS of multiple polymorphs to predict these transitions. This analysis calls for simulations at finite temperatures, and has not been included in the present study.

In summary, the energy–volume curves of over 200 elemental, binary, and ternary crystalline solids were calculated using DFT, and the resulting data were fit to several theoretical EOS commonly cited in the literature. Although the quality of fit, as measured by RMSrD, did not vary greatly across the investigated set of equations, the Birch (Eulerian), Tait, and Vinet equations were found to give the best overall quality of fit to calculated energy–volume curves as compared to the other equations under examination. Band gap and bulk modulus were not found to be useful indicators of EOS quality of fit for the aggregate set of materials, although we observed that quality of fit does vary with structure for polymorphs within certain chemical systems. Bulk modulus values derived from the calculated EOS were benchmarked against experimental data, and in general display good agreement.

Methods

The calculation of EOS is automated using self-documenting workflows compiled in the atomate31 code base that couples pymatgen32 for materials analysis, custodian33 for just-in-time debugging of DFT codes, and Fireworks34 for workflow management. The EOS workflow begins with a structure optimization and subsequently calculates the energy of isotropic deformations, including ionic relaxation with volumetric strain ranging from from −33 to 33% (−10 to 10% linear strain) of the optimized structure. Density-functional-theory (DFT) calculations were performed as necessary using the projector augmented wave (PAW) method35,36 as implemented in the Vienna Ab Initio Simulation Package (VASP)37,38 within the Perdew–Burke–Ernzerhof (PBE) Generalized Gradient Approximation (GGA) formulation of the exchange-correlation functional.39 A cutoff for the plane waves of 520 eV is used and a uniform k-point density of approximately 7,000 per reciprocal atom is employed. Convergence tests were performed for selected materials across a range of bulk modulus values, with KPPRA values between 1,000 and 11,000; plots are provided in the SI (Supplementary Figure S12). In addition, standard Materials Project Hubbard U corrections are used for a number of transition metal oxides,40 as documented and implemented in the pymatgen VASP input sets.32 We note that the computational and convergence parameters were chosen consistently with the settings used in the Materials Project41 to enable direct comparisons with the large set of available MP data.

Data availability

Numerical EOS for the data set investigated in this study have been included as a Supplementary json File (see explanation of file structure in SI). The equivalent data are also available for free to the public, via the Materials Project online database.

Any additional data (compiled experimental values, calculated fitting parameters, etc.) are available from the corresponding author upon request.