Introduction

The calculation of electronic band structures using density functional theory (DFT) is now so routine that it is becoming faster to compute certain physical properties than make samples and measure them—inspiring the materials genome initiative efforts worldwide. Ab initio calculations are important from a materials’ design perspective in that they provide insight into the underlying electronic states that give rise to experimentally measurable properties. Dielectric, optical and transport properties such as electrical conductivity, Hall effect, and thermoelectric power (Seebeck effect) require knowledge not only of the electronic structure readily available from ab initio calculations, but may also require an assumption about the scattering. Using a constant relaxation time approximation, very precise predictions of transport properties that depend on fine details of the band structure can be made, however, the electrical conductivity predicted for instance can be greatly misleading because the relaxation time is approximated, often to an arbitrary constant. A recent study performed by the authors demonstrated that while Seebeck coefficient was reproduced fairly well across a variety of compounds (provided that the band gap was not severely underestimated), the experimental values on conductivities can be highly inaccurate using a constant relaxation time.1 While some scattering mechanisms can now be calculated using ab initio methods, they are far from routine and require special algorithms. The goal of this study is to extract transport information from band structure calculations that does not depend on any scattering assumption.

In the common free-electron approximation lexicon of electronic and optical properties we typically describe charge carriers as having an effective mass m * and a relaxation or scattering time τ. Combining with the density of carriers n, the electrical conductivity σ = ne 2 τ/m * and drift mobility μ d = eτ/m* can also be expressed. This description, while not exact, has proven immensely helpful in the understanding and engineering of electronic materials that have profoundly changed our civilization. This representation already separates transport into electronic structure (through the m*) and scattering (τ) terms as well as allowing the flexibility of varying n (through doping, for example). It is, therefore, natural to expect that knowledge of electronic structure should reveal the appropriate effective mass for various values of n but not necessarily the scattering-dependent transport properties (such as σ and μ d) until the scattering is known.

The free-electron description has been integral to semiconductor physics despite many examples of profound deviations. In the free-electron model the electronic structure is represented by a single, isotropic Fermi surface described by particle with mass and charge of an electron. A free-electron like description is only helpful to describe real semiconductors if we allow multiple (N v) free-electron like pockets to describe the Fermi surface and that each pocket may be anisotropic (described by anisotropy term K) with effective mass m * that differs from free-electron mass. Because of the multiple pockets the total density of electronic states will be N v times that of a single pocket.

In thermoelectrics, for example, these and other material parameters are helpful to predict the promise of a material for use in a thermoelectric device.2,3,4 For typical semiconductor transport where the electrons are scattered by acoustic phonons (deformation potential scattering)5 the thermoelectric quality factor B, given by:

$$B=\frac{2{k}_{{\rm{B}}}^{2}{\hslash}}{3\pi }\,\frac{{N}_{{\rm{v}}}}{{m}_{{\rm{c}}}^{\ast }\,}\,\frac{{C}_{l}}{{\kappa }_{{\rm{L}}}{{\Xi}}^{2}}T$$
(1)

determines the maximum zT (materials efficiency) when the semiconductor is optimally doped, where κ L is the lattice thermal conductivity, Ξ is the deformation potential, C l is the average longitudinal elastic modulus, \({m}_{\rm c}^{\ast }\) is the conductivity effective mass, and T is temperature.

Two materials parameters, valley degeneracy N v and conductivity effective mass \({m}_{\rm c}^{\ast }\) appear in the quality factor that concern the static band structure and should be accessible by DFT. A small conductivity effective mass \({m}_{\rm c}^{\ast }\) should lead to higher mobility,6 and have led to the reinvestigation of structures with very light bands such as SnTe.7 Valley degeneracy (N v) has been shown to be critical for achieving high zT.8,9,10,11,12 Many of the best thermoelectric materials are known to have, recently have been found to have, or are being engineered to have high valley degeneracy, including: the lead and tin chalcogenides,5, 10, 13 diamond like copper selenides,14, 15 Skutterudites,16 Mg2Si,11, 17 Half Heuslers,18 and Zintl phases.19 While isolated pockets of Fermi surfaces can improve the quality factor, Fermi surface pockets connected by threads in the lead chalcogenides20 and the complex Fermi surfaces of bismuth telluride21 have also been suggested to be beneficial for zT.

Here, we show that DFT calculations can be used to compute two types of effective masses characteristic of the electronic structure independent of the scattering mechanism. An inertial mass \({m}_{\rm c}^{\ast }\) from the electrical conductivity and a density of states (DOS) mass \({m}_{\rm S}^{\ast }\) from the Seebeck coefficient and carrier concentration. Then we introduce the ratio of these two masses as the Fermi Surface complexity factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })={({m}_{{\rm{S}}}^{\ast }/{m}_{{\rm{c}}}^{\ast })}^{3/2}\), which we recognize as related to valley degeneracy N v and carrier pocket anisotropy K.

Results

Boltztrap conductivity mass \(({m}_{{\rm{c}}}^{\ast })\)

The conductivity effective mass is computed directly from the Boltztrap calculation for electrical conductivity, \({({m}_{{\rm{c}}}^{\ast })}^{-1}=\sigma /n{e}^{2}\tau\) using the constant relaxation time approximation (CRTA). This definition has been used to conduct a high-throughput search for low hole and electron low effective mass (high mobility) transparent conductive oxides22,23,24 and also for analyzing specific thermoelectric materials.25, 26 Specifically using the notation of Madsen and Singh27 the effective mass tensor can be computed from Eq. (12) of ref. 27

$${({m}_{{{\rm{c}}}_{\alpha \beta }}^{\ast }(T;\mu ))}^{-1}=\frac{{\sigma }_{\alpha \beta }(T;\,\mu )}{{e}^{2}\tau }\times \frac{1}{n(T;\,\mu )}$$
(2)

Where e is the electron charge and τ is the user-specified constant relaxation time. When multiple bands contribute to conduction, \({m}_{{\rm{c}}}^{\ast }\) is a weighted average over all contributing bands.

The net charge carrier concentration n (or doping concentration) is measured relative to a band edge and is a positive quantity whether electrons or holes are dominant charge carriers. In BoltzTraP, N val, the number of valence electrons/cell required to place the Fermi level in the band gap to make the material “undoped” at 0 K is set by the user. Thus \(\frac{{N}_{{\rm{val}}}}{V}={\int }^{}g({\epsilon }){f}_{\mu ={\rm{undoped}}}(T=0\,K;{\epsilon })d{\epsilon }\) where V is the volume of the unit cell (cm3), \(g({\epsilon })\) is the density of states (states/volume/Energy), and \({f}_{\mu ={\rm{undoped}}}(T;{\epsilon })\) is the Fermi-Dirac distribution function where the electron chemical potential (μ or E F) is that of the undoped material. The doping concentration is then \(n=|\frac{{N}_{{\rm{val}}}}{V}-{\int }^{}g({\epsilon }){f}_{\mu }(T;{\epsilon })d{\epsilon }|\) using the notation of Madsen and Singh,27which is directly computed from the N in the BoltzTrap output as n(T; μ) = (|N(T; μ)|)/(V).

The conductivity mass tensor (\({m}_{{\rm{c}}}^{\ast }\)) should be a good representation of the band structure relevant to electrical conductivity independent of the scattering mechanism. This is a more relevant output from Boltztrap than conductivity (σ) as CRTA is typically a poor approximation for scattering in real thermoelectric materials. Also while σ changes rapidly in a semiconductor with differing Fermi level (or n), \({m}_{{\rm{c}}}^{\ast }\) should be constant to a first-order approximation as demonstrated in Fig. 1 making it a more robust descriptor of the BoltzTraP calculation result. Like conductivity, the drift mobility μ d requires knowledge of the scattering through τ. Thus, while mobility could be easily computed from BoltzTraP:

$${\mu }_{{{\rm{d}}}_{\alpha \beta }}(T;\mu )=\frac{{\sigma }_{\alpha \beta }(T;\mu )}{e}\times \frac{1}{n(T;\mu )}$$
(3)

the uncertainty of τ makes effective mass \({m}_{{\rm{c}}}^{\ast }\), not mobility μ d, the parameter that most directly represents the electronic structure.

Fig. 1
figure 1

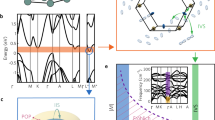
Effective masses and complexity factor at 300 K from BoltzTraP for some relatively simple structures CdTe (a–e) and AlAs (f–j). a, f Computed electronic band structure, b, g Conductivity mass, m*c, versus Fermi level and Seebeck DOS mass, m*S, as functions of the Fermi level across the valence and conduction bands. c, h Fermi surface complexity factor \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) and true valley degeneracy N v. d, i Primary conduction Fermi surface (0.03 eV above the conduction band edge (CBM) in CdTe and 0.1 eV above the band edge for AlAs), and e, j Valence band Fermi surface (0.05 eV below the valence band edge (VBM) for both CdTe and AlAs). The valence band Fermi surfaces are colored differently for the three degenerate bands

Full size image

Note that the effective mass \({m}_{{\rm{c}}}^{\ast }\) used here differs from the commonly used definition involving the second derivative of a particular band dispersion: \(1/{m}_{\alpha \beta }^{\ast }=(1/{\hslash }^{2})({\partial }^{2}E/\partial {k}_{\alpha }\,\partial {k}_{\beta })\) either evaluated at a particular k-point (energy) or evaluated at the band edge. In general, particularly for complex band structures, these varying definitions can give different values for effective mass. It is mathematically equivalent (by integration by parts28) to use the second derivative mass, but one must remember that this second derivative mass must be averaged over the entire band of filled states at 0 K. Thus using the second derivative, the effective mass \({m}_{{{\rm{c}}}_{\alpha \beta }}^{\ast }(T;\mu )\) requires an integration over all states weighted by the Fermi function.23 While \({m}_{{\rm{c}}}^{\ast }\) is a good measure of the average inertial effective mass of electrons in a system, it does not indicate much about the density of electronic states in a system that has multiple bands.

Boltztrap Seebeck mass (\({m}_{{\rm{S}}}^{\ast }\))

The effective density of electronic states can be estimated through the Seebeck coefficient characterized by the DOS effective mass: \({m}_{{\rm{S}}}^{\ast }\).26 This can be performed in analogy to the Pisarenko plot (S vs n), which is commonly used to estimate an effective mass \({m}_{{\rm{S}}}^{\ast }\) from experimental data.29, 30 Treating the BoltzTraP transport results as if it were experimental data, we solve for an effective reduced chemical potential η eff that yields the computed Seebeck coefficient. For each BoltzTraP calculated pair of S(T; μ) (using 1/3 the trace of the S ij (T; μ) tensor of Eq 16 in Madsen and Singh27) and n(T; μ) we solve for a \({m}_{{\rm{S}}}^{\ast }\)(T; μ). First, from S(T; μ) we find the reduced chemical potential η eff that would give that same Seebeck coefficient for a single parabolic band:

$$S(T;\mu )=\frac{{k}_{{\rm{B}}}}{q}\left[\frac{(2+\lambda )}{(1+\lambda )}\frac{{F}_{1+\lambda }({\eta }_{{\rm{eff}}})}{{F}_{\lambda }({\eta }_{{\rm{eff}}})}\,-{\eta }_{{\rm{eff}}}\right]$$
(4)

Where λ is the scattering exponent, q is −e for electrons and + e for holes, and F 1+λ are the Fermi functions given by:

$${F}_{j}(\eta )={\int }_{0}^{\infty }\frac{{{\epsilon }}^{j}\,d{\epsilon }}{1+{e}^{{\epsilon }-\eta }}$$
(5)

We adjust the common scattering assumption, which is usually by acoustic phonons in experiments, to coincide with the CRTA used in BoltzTraP (i.e., set λ = 1/2). The reduced chemical potentials (η eff = (μ − E B)/(k B T)) are relative to the band edge where E B is the energy of the (valence or conduction) band edge and the sign of η is always such that η eff > 0 has chemical potential (μ in Madsen and Singh;27 E F in BoltzTraP output) in the band.

Then, using the effective reduced chemical potential η eff, we find the effective mass \({m}_{{\rm{S}}}^{\ast }\)(T; μ) that would give the n(T;μ) calculated from Boltztrap.

$$n(T;\mu )=\frac{1}{2{\pi }^{2}}{\left(\frac{2{m}_{{\rm{S}}}^{\ast }(T;\mu ){k}_{{\rm{B}}}T}{{\hslash }^{2}}\right)}^{\frac{3}{2}}{F}_{1/2}({\eta }_{{\rm{eff}}})$$
(6)

It should be noted that \({m}_{{\rm{S}}}^{\ast }\) is a scalar quantity and not a tensor unlike \({m}_{{{\rm{c}}}_{\alpha \beta }}^{\ast }\). Although the Seebeck coefficient S ij (T;μ) is a tensor, for parabolic bands of the same sign, and for τ that may depend on energy but not direction,26 the Seebeck only depends on the reduced chemical potential η eff and the scattering exponent λ both of which are scalars. Considering that the density of states \(g({\epsilon })\), is also a scalar quantity it is appropriate that a density of states effective mass such as \({m}_{{\rm{S}}}^{\ast }\) should also be a scalar quantity. This single parabolic band Seebeck coefficient likely represents the thermopower from the configurational entropy of the electrons in the available states represented by \(g({\epsilon })\), which would support our interpretation of \({m}_{{\rm{S}}}^{\ast }\) as an appropriate measure of the density of states effective mass.

The density of states effective mass is a convenient single metric to describe the density of states. Like \({m}_{{\rm{c}}}^{\ast }\), \({m}_{{\rm{S}}}^{\ast }\) remains relatively constant with doping while S, σ, g, n change, and, therefore, \({m}_{{\rm{S}}}^{\ast }\) is a better descriptor of the density of states for semiconductors than any single value of g (recall that \(g({\epsilon })=(8\,\pi \sqrt{2}/{h}^{3}){m}^{\ast 3/2}\sqrt{{\epsilon }}\) is a typical description for g of a semiconductor). Even though there may be multiple or nonparabolic bands, a single effective mass is the best first order characterization of a semiconductor and is accurate within the uncertainty of measurements on new materials. Particularly for use in thermoelectrics, \({m}_{{\rm{S}}}^{\ast }\) is anticipated to be more relevant than an effective mass from a direct comparison to the calculated density of states (g)2 because it most directly relates to the Seebeck coefficient both in theory and experiment.

Effective valley degeneracy \(({N}_{{\rm{v}}}^{\ast })\)

A Fermi surface consisting of N v identical, isolated surfaces will have total number of electronic states that is N v times the number of states in each isolated surface. If each isolated surface can be described with a density of states mass m*b(recall \(g({\epsilon })\propto \,{m}_{b}^{{\ast }^{3/2}}\)) for each band or pocket then the total density of states mass, here computed using the Seebeck coefficient, is \({m}_{{\rm{S}}}^{\ast }={N}_{{\rm{v}}}^{2/3}{m}_{{\rm{b}}}^{\ast }\). Valley degeneracy then manifests itself by increasing the density of states effective mass relative to the single valley effective mass (m*b), which should be related to the inertial mass \({m}_{{\rm{c}}}^{\ast }\). Symmetry imposed valley degeneracy results from band extrema that exist at low symmetry points in a high symmetry crystal or orbital degeneracy of the constituent atoms. In order to maximize N v, the band extrema should be off high symmetry points (such as gamma), which is influenced by the symmetry of the most relevant atomic orbitals.31

When multiple bands contribute to conduction but they are not exactly degenerate (band extrema not at the same energy), we consider this an increased effective valley degeneracy. One can approximate \({N}_{{\rm{v}}}^{\ast }\) by counting the total number of charge carrier Fermi surfaces (as in done for calculating N v in Figs. 1 and 2, or within a particular energy window.2 We think of effective valley degeneracy, \({N}_{{\rm{v}}}^{\ast }\), as describing the effective number carrier pockets contributing to conduction, where the contribution may only be partial if that pocket is displaced by more than ~k B T from the chemical potential (μ).

Fig. 2
figure 2

Band structure, m*c and m*S versus Fermi level, and \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) at 300 K versus Fermi level, and valence and conduction band Fermi surfaces for PbTe (a–e), PbSe (f–j), and PbS (k–o). The valence and conduction band edges are shown as a dashed line. Fermi surfaces are drawn at 0.1 eV above the conduction band edge (CBM) for PbTe, PbSe, and PbTe, respectively, or 0.13, 0.3, and 0.4 eV below the valence band edge (VBM) for PbTe, PbSe, and PbS, respectively

Full size image

Effective anisotropy factor (K *)

Only in the simplest cases can Fermi surfaces can be described as spherical pockets; many materials contain more complicated Fermi surfaces. The next level of complexity involves ellipsoidally shaped pockets where the anisotropy parameter, \(K={m}_{\parallel }^{\ast }/{m}_{\perp }^{\ast }\), quantifies the degree of anisotropy.32 Many material systems have been shown to display K different from unity including: Si/Ge,33, 34 IV–VI materials,32, 35, 36 III–V materials,37 and others.38 The conductivity effective mass of such systems is calculated from the harmonic average along each direction: \({m}_{{\rm{c}}}^{\ast }=3{({m}_{\parallel }^{{\ast }^{-1}}+2{m}_{\perp }^{{\ast }^{-1}})}^{-1}\), which determines the carrier mobility \((\mu =e\tau /{m}_{{\rm{c}}}^{\ast })\). The conductivity mass \({m}_{{\rm{c}}}^{\ast }\) is, in general, different from the single valley density of states mass m*b (geometric average: \({m}_{{\rm{b}}}^{\ast }={({m}_{\parallel }^{\ast }{m}_{\perp }^{{\ast }^{2}})}^{1/3}\)); they are equal only for spherical pockets (\(K={m}_{\parallel }^{\ast }/{m}_{\perp }^{\ast }=1\)). For non-ellipsoidally shaped Fermi surfaces, we can define the effective anisotropy parameter K * in terms of the effective masses:26

$${K}^{\ast }={\left(\frac{{m}_{{\rm{b}}}^{\ast }}{{m}_{{\rm{c}}}^{\ast }}\right)}^{3/2}=\frac{{(2K+1)}^{3/2}}{{3}^{3/2}K}\,$$
(7)

Fermi surface complexity factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\)

Combining the effects of valley degeneracy \({N}_{{\rm{v}}}^{\ast }\) and anisotropy K * we define the Fermi surface complexity factor, \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) in terms of the effective masses \({m}_{{\rm{c}}}^{\ast }\) and \({m}_{{\rm{S}}}^{\ast }\) we derive from DFT calculations:

$$({N}_{{\rm{v}}}^{\ast }{K}^{\ast })={\left(\frac{{m}_{{\rm{S}}}^{\ast }}{{m}_{{\rm{c}}}^{\ast }}\right)}^{3/2}$$
(8)

Although it is not clear how to define the single valley effective mass (m*b) in general, for simple cases of multiple, degenerate, ellipsoidal Fermi surface pockets we concluded \({N}_{{\rm{v}}}^{\ast }={({m}_{{\rm{S}}}^{\ast }/{m}_{{\rm{b}}}^{\ast })}^{3/2}\) and \({K}^{\ast }={({m}_{{\rm{b}}}^{\ast }/{m}_{{\rm{c}}}^{\ast })}^{3/2}\). So while we do not to calculate or even clearly define \({N}_{{\rm{v}}}^{\ast }\) or K * individually, we can clearly define \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) through the equation above. Because \({m}_{{{\rm{c}}}_{\alpha \beta }}^{\ast }\) is, in general, a tensor while \({m}_{S}^{\ast }\) is a scalar, \({({N}_{{\rm{v}}}^{\ast }{K}^{\ast })}_{\alpha \beta }\) is most generally a second rank tensor like \({m}_{{{\rm{c}}}_{\alpha \beta }}^{\ast }\). For simplicity in this work, only isotropic compounds are demonstrated below so that only scalar values are needed.

The Fermi surface complexity factor \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) can be a good indicator of the effective valley degeneracy \({N}_{{\rm{v}}}^{\ast }\). Compared to the valley degeneracy \({N}_{{\rm{v}}}^{\ast }\), which can easily be three or more, the anisotropy factor K *, in some cases, may only lead to small deviations from unity, resulting in a complexity factor \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\)≈ \({N}_{{\rm{v}}}^{\ast }\). For ellipsoidal Fermi pockets a factor of two difference in the directional effective mass, \({m}_{\parallel }^{\ast }/{m}_{\perp }^{\ast }=2\), results only in K * = 1.08 while a highly anisotropic \({m}_{\parallel }^{\ast }/{m}_{\perp }^{\ast }=12\) is required to get just K * = 2.

The Fermi surface complexity factor \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) may also be a good indicator of the suitability of a material for thermoelectrics as noted by Parker et al.26 who also considered a ratio similar to \({m}_{{\rm{S}}}^{\ast }\)/\({m}_{{\rm{c}}}^{\ast }\). Complex Fermi surfaces have been shown to be beneficial for zT. Complexity in the form of high valley degeneracy N v (multiple carrier pockets in the Fermi surface contributing to conduction) such as found in PbTe39 is widely recognized to be beneficial to thermoelectric performance as seen in the quality factor. However, other complexities such as narrow threads of Fermi surface has also been identified to improve thermoelectric transport.20, 36, 40, 41

The advantage of anisotropy factor K * may be most apparent when the scattering is also complex. Separating the scattering time τ 0 from the quality factor42] results in a quality factor strongly dependent on \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\):

$$B=\frac{{k}_{{\rm{B}}}^{2}T{({k}_{{\rm{B}}}T)}^{3/2}}{3{\pi }^{2}{\hslash }^{3}}\frac{{\tau }_{0}}{{\kappa }_{{\rm{L}}}}{N}_{{\rm{v}}}^{\ast }{K}^{\ast }{({m}_{{\rm{c}}}^{\ast })}^{1/2}$$
(9)

In these cases where the Fermi surface has additional complexity beneficial to thermoelectrics, \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) may be an auspicious metric for thermoelectric materials.

Discussion

II–VI and III–V Materials—CdTe and AlAs

As a first example, the conduction band of CdTe is centered directly at Γ (N v = 1) and has a spherical Fermi surface (as shown in Fig. 1d). This simple band structure shows the effective masses (\({m}_{{\rm{S}}}^{\ast }\) and \({m}_{{\rm{c}}}^{\ast }\)) as computed from calculated Boltztrap data (shown in Fig. 1 as described earlier) are constant with varying doping (Fermi level) and roughly consistent with experimental and traditionally calculated values of m*.43 The Fermi surface complexity factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) also shown in Fig. 1c is very close to 1 for the conduction band, consistent with a single (\({N}_{{\rm{v}}}^{\ast }\) = 1) spherical pocket (K * = 1). The computed \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) is approximately 1 over a wide range of Fermi levels even as the Fermi level is moved deeper into the Γ band. A slight decrease in value and increase in noise is observed as the Fermi level moves farther into the band presumably due to sensitivity of \({m}_{{\rm{S}}}^{\ast }\) to the small variations in Seebeck at these Fermi levels.

Next, consider the slightly more complicated conduction band of AlAs, which has multiple carrier pockets at different points in the Brillouin zone (Fig. 1i), as the Fermi level is moved into the conduction band. The AlAs Fermi surface for the primary conduction band at X has multiple pockets (N v = 3) (Fig. 1i). We calculate \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })=3.5\) near the conduction band edge consistent with our expectation of N v ~ 3 and K* close to 1.

One might expect that \({N}_{{\rm{v}}}^{\ast }\) should make a stepwise transition from one value of N v to another as the Fermi level approaches and enters the additional band. This behavior is observed in Fig. 1h where \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) is compared to a hypothetical N v just by considering the symmetry of the extrema alone (green line in Fig. 1g, \({N}_{{\rm{v}}}({E}_{{\rm{F}}})={\sum }^{}{N}_{{\rm{v}},i}{\rm{H}}({E}_{{\rm{F}}}-{E}_{{\rm{i}}})\) where H is the Heaviside step function and E i is the energy of the i th band extrema).2 As the Fermi level moves into the conduction band, we reach the Γc (N v = 1, 0.28 eV above X c) and L c (N v = 4, 0.51 eV above X c) bands where the total N v increases to 4 and 8, respectively. The Fermi surface complexity factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) increases steadily from the band edge resulting in a value of 3.5 and 6.1 at the Γc and L c band edge energies, respectively. The thermoelectric Fermi surface complexity factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) mirrors the true N v both qualitatively and quantitatively—consistent with an anisotropy component, K *, that is not far from unity. The Supplementary material includes \({m}_{{\rm{S}}}^{\ast }\), \({m}_{{\rm{c}}}^{\ast }\), N v, \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) for the other III–V materials (Table S1).

Enhancement in K * appears in the valence band of both CdTe and AlAs, which consist of three degenerate bands: Γ1,2,3v, with different effective masses (light hole, heavy hole, and split-off band) due to p-orbital degeneracy.31 As a result, the Fermi surface—even though it is centered at the Γ point—will have a non-trivial topology (as described by Mecholsky et al.41 for silicon), which appears to result in a larger K * component to the Fermi surface complexity factor and a \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) that exceeds the expected degeneracy of N v = 3 for Γ1,2,3v. For the valence band, \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) = 6 and 9 for CdTe and AlAs, respectively. Mecholsky et al.41 shows that warped, non-ellipsoidal Fermi surfaces, which result from the combination of light and heavy bands, significantly influence the electronic transport in these systems altering the equivalent effective masses.

IV–VI Materials—PbS–PbSe–PbTe

The lead chalcogenides (including PbTe, PbSe,42, 44 PbS,45 and their alloys46,47,48,49,50,51,52,53,54) are known to be good thermoelectric materials partly because of their complex electronic structure. The Fermi surface complexity factor and effective masses were also computed for these IV–VI compounds. For PbS and PbSe, the conduction band at the L-point shows significant valley degeneracy of N v = 4 shows \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }=4\) as expected for chemical potential near the band edge. The primary valence band, also with N v = 4 has a nearby secondary valence band along the Σ line, with its own N v = 12, which can be seen by a rapidly rising \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) that approaches the simple sum of these valley degeneracies.

An exceptionally high \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) is also found in p-type PbTe, above that expected from \({N}_{{\rm{v}}}^{\ast }\) of L and Σ bands indicating a significant contribution from K * or a new band. In p-type PbTe the complex Fermi surface characterized by threads which develop between the L -v and Σ −v pockets, which have been concluded to contribute to the high thermoelectric performance.8, 55,56,57,58,59 This could be due to the large surface area to volume ratio of the thread-like states, which leads to an inherently large mobility and quality factor (and corresponding large K*). Compared to PbS and PbSe, the bands in PbTe are closer in energy (e.g., the L and Σ bands are computed to be only ~ 0.12 eV apart) and these energies may change with temperature. For example, in PbTe, the L and Σ bands are thought to shift with temperature, eventually converging at ~ 700 K (ref. 56).

High-throughput computation

The vast electronic structure database constructed through the Materials Project allows for large-scale screening of semiconductors for thermoelectrics, transparent conductors as well as other applications. By combining DFT and BoltZtraP (using the CRTA) thousands of compounds can be screened for effective mass (\({m}_{{\rm{c}}}^{\ast }\), \({m}_{{\rm{S}}}^{\ast }\)) and complexity factor \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) (Supplementary Table I).

Figure 3 shows the correlation between \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) and the calculated maximum (Fermi level-dependent) power factor (assuming constant τ = 10−14 s) for the large group of compounds (~ 2300 isotropic compounds) at 600 K. We can see a good correlation between the calculated Fermi surface complexity factor and the maximum attainable power factor; this is expected since the quality factor for constant relaxation time is expected to scale according to Eqn. 9. Data regarding the maximum power factor and \({N}_{{\rm{v}}}^{\ast }{K}^{\ast }\) is included in the Supplementary material.

Fig. 3
figure 3

Maximum power factor for ~ 2300 cubic compounds plotted as a function of the Fermi surface complexity factor (evalulated at the Fermi level which yields the maximum power factor) at T = 600 K

Full size image

While experimental conductivity values are difficult to reproduce within the constant relaxation time,1 it is remarkable that known thermoelectric materials such as PbTe, GeTe, TiCoSb show up with a high constant relaxation time power factor and a high Fermi surface complexity factor. This indicates that, at least for screening and ranking, the Fermi surface complexity factor is an effective descriptor.

Conclusions

Both a density of states effective mass, \({m}_{{\rm{S}}}^{\ast }\) and inertial effective mass \({m}_{{\rm{c}}}^{\ast }\) can be extracted even from complex DFT band structures using the result of σ and S transport calculations, such as done in BoltzTraP, even if the scattering mechanism is not known. Because \({m}_{{\rm{c}}}^{\ast }\) and \({m}_{{\rm{S}}}^{\ast }\) are less influenced by τ and scattering mechanism than σ and S, they are better descriptors of a band structure’s contribution to transport than a CRTA value of σ and S itself. We interpret the ratio of these two masses as a Fermi Surface Complexity Factor \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\), which should be influenced by effective valley degeneracy \({N}_{{\rm{v}}}^{\ast }\) and anisotropy K *, both beneficial to thermoelectric performance.

We have analyzed the maximum thermoelectric power factors and for a large set compounds from the Materials Project to show that \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) appears to correlate well with thermoelectric performance. A larger than expected \(({N}_{{\rm{v}}}^{\ast }{K}^{\ast })\) is found in the lead chalcogenide semiconductors, is likely as a result of non-trivial topological features of the Fermi surface. Combining high-throughput DFT with Boltztrap calculations to extract commonly understood quantities such as effective mass from band structures have the potential to impact many applications. By predicting how these properties evolve with doping and chemistry will enable future band engineering for even broader use.

Methods

Ab initio computations in this section are from the Materials Project database60 and use DFT within the generalized gradient approximation (GGA) or GGA + U in some compounds1 in the Perdew–Burke–Ernzheroff formulation.61 Calculations were performed using the VASP software and projector augmented-wave pseudopotentials.62 Bolztrap calculations were computed using the open-source code27 along with analysis and plotting software from pymatgen.63

High-throughput calculations of the Fermi surface complexity factor are analyzed in Fig. 3, but we limit the analysis to isotropic compounds (maximum deviation in the eigenvalues of the power factor tensor of <3% along any direction) and those with a maximum optimum carrier concentration <1 × 1021 cm−3. We also chose to remove compounds that were not particularly stable or those that were metallic (we required that the energy above the convex hull be <0.05 eV/atom, and that the band gap be >0.03 eV). The entire Fermi Surface Complexity Factor results for calculations at 600 K (with unstable compounds removed) is included in the Supplementary material under the conditions: 1 × 1020 cm−3, maximum power factor conditions, and maximum zT conditions (assuming τ = 1 × 10−14 s and κ L = 0.5(W)/(m−K)).

The band structures we used do not include spin-orbit coupling effects. However, our approach to compute effective masses and Fermi surface complexity could easily be applied on data generated with spin-orbit coupling.

Additional calculation details specific to the III–V or IV–VI materials are included in the Supplementary material.