Abstract
The phase diagram of hole-doped high critical temperature superconductors as a function of doping and temperature has been intensively studied with chemical variation of doping. Chemical doping can provoke structural changes and disorder, masking intrinsic effects. Alternatively, a field-effect transistor geometry with an electrostatically doped, ultra-thin sample can be used. However, to probe the phase diagram, carrier density modulation beyond 1014 cm−2 and transport measurements performed over a large temperature range are needed. Here we use the space charge doping method to measure transport characteristics from 330 K to low temperature. We extract parameters and characteristic temperatures over a large doping range and establish a comprehensive phase diagram for one-unit-cell-thick BSCCO-2212 as a function of doping, temperature and disorder.
Similar content being viewed by others
Introduction
High-temperature cuprate superconductors display a rich phase diagram, explored using a variety of techniques including transport1,2,3,4, by varying chemical doping. Their parent compounds are known to be strongly correlated with antiferromagnetic ordering at low temperatures. As doping is increased this ordering temperature falls, eventually giving place to fluctuations, as superconductivity sets in at lower temperatures. The superconducting temperature increases with doping until an optimal value and then falls, following a dome-like shape, until superconductivity is suppressed. Meanwhile, at higher temperatures the non-superconducting state remains intriguing. In the underdoped regime, a pseudogap in the electronic excitation spectrum, possibly related to the formation of superconducting pairs, has been shown to exist. The temperature below which this pseudogap state opens decreases with doping. Near the optimal doping level and above the superconducting temperature, the material is thought to exist in a “strange” metallic phase in the sense of a deviation from Fermi liquid behavior as seen from the linear dependence of resistivity on temperature. Finally, as doping is further increased and superconductivity is suppressed, Fermi liquid behavior is progressively established.
As chemical doping is a source of disorder and structural change, alternative doping methods have been sought. To match the chemical doping levels with electrostatic doping, intense electric fields ~109 V⋅m−1 and high carrier density modulation are required. In recent years, pioneering efforts have been made using ionic liquids5, 6 or ferroelectrics as the dielectric to investigate the La2−x Sr x CuO4 and YBa2Cu3O7−x families of materials7,8,9,10. Considerable change in the doping and critical temperature have been obtained and the insulator–superconductor transition in these materials has been investigated through transport measurements. However, for transport measurements the ionic liquid method is only relevant well below room temperature because of the conductivity of mobile ions in the liquid state. This precludes its use for establishing a temperature vs. doping phase diagram.
In the following, we use an alternative electrostatic doping method, namely, space charge doping11, 12, achieving carrier density modulation up to 1015 cm−2 and measure transport up to 330 K. We detect superconductivity in the two-dimensional limit in one-unit-cell-thick samples and investigate the effects of doping, temperature, and disorder to establish a comprehensive phase diagram of BSCCO-2212.
Results
Sample characterization
BSCCO-2212 two-dimensional (2D) crystals with lateral size of ~100 μm and thickness ranging from 1 to 2.5 unit cells (u.c.) were fabricated by the anodic bonding method on 0.5 mm-thick soda-lime glass substrates13, 14, using a bulk single crystal precursor with stoichiometry Bi2.1Sr1.9CaCu2O8+x and a critical temperature of 89 K determined by magnetic susceptibility measurements. Contacts were deposited by evaporating 100 nm of gold through stencil shadow masks previously aligned on the sample. We thus avoid chemical pollution and surface contamination from standard lithography techniques, which in our experience can irreversibly degrade the quality of BSCCO-2212 2D crystals. We performed transport measurements with the four-wire Van der Pauw geometry in a high vacuum cryostat coupled to an external 2 T electromagnet for Hall measurements.
Here we show results for four different devices with thickness varying from 3 nm (1 u.c.) to ~7 nm (2.5 u.c.) as established by atomic force microscopy (AFM) and optical contrast. BSCCO-2212 cleaves at the BiO layer so that ultra-thin samples are expected to be multiples of 0.5 u.c. with one pair of CuO2 planes per half unit cell. The thinnest samples fabricated were 0.5 u.c. and were systematically insulating. All devices shown in this work were superconducting at the outset, including the 1 u.c. device. The initial magnitude of resistivity varied, ranging from 5 × 10−4 to 5 × 10−3 Ω⋅cm depending on the device. We attribute this variation to the fabrication process, which can induce mechanical disorder caused by substrate roughness and eventually varying doping due to partial oxygen loss. At the start of the measurements, each device was annealed at 340–350 K (the temperature T d at which devices are doped) for a few hours at 10−6 mbar causing a decrease of the monitored sheet resistance R S probably due to removal of eventual surface contamination. An increase of R S would have indicated oxygen loss, not observed at this temperature. We thus control carrier density exclusively by our electrostatic doping mechanism with no change in stoichiometry or disorder during the doping process.
Space charge doping of 2D BSCCO-2212 crystals
Doping is tuned by monitoring R S at the temperature T d by applying a gate voltage V G of the order of 100–280 V between the device and a metallic electrode on the opposite face of the glass substrate. The gate voltage creates an ionic space charge at the glass–device interface (Fig. 1a). Carrier concentration in the device can be fixed by lowering the temperature below T d, thus freezing the accumulated space charge at the interface and annulling ionic mobility in the glass substrate (Supplementary Note 1). For a given carrier concentration, the temperature dependence of R S is measured from 330 K down to well below T c, defined here as the temperature below which the resistivity is zero.
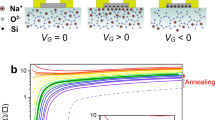
Overview of space charge doped BSCCO-2212 2D crystals. a Schematic top and side view of devices. b R S(T) for the four devices of this study at varying doping levels controlled by the gate voltage V G. Curves corresponding to the initial doping are indicated with stars; the underdoped region corresponds to cyan-blue curves, whereas the overdoped region corresponds to yellow-brown curves; R S curves corresponding to the optimal doping level are plotted in thick green lines. Though samples A and D have not been swept through the optimal doping point, the fact that their initial doping is optimal is confirmed by the Hall coefficient measured in these samples as shown in Table 1
A central question is the evaluation of the carrier concentration (n S). We perform Hall effect measurements and use 1/qR H to approximately evaluate n S (Supplementary Note 2). This value is indicative of the change introduced by doping and not an absolute measure of the carrier density since the electronic structure at the Fermi surface and its evolution with doping and temperature is complex and cannot be approximated by a single parabolic band. The Fermi surface evolves from hole-like to electron-like with doping and the contributions of these surfaces to the Hall coefficient are temperature dependent15,16,17. To minimize errors related to this dependence, we consider R H values at the fixed, low temperature of 120 K18, 19 for all doping values. Figure 1 shows an overview of the R S vs. T characteristics as a function of space charge doping for the four devices of this study. We achieve a large, reversible variation in carrier density and hence in R S and T c by applying positive and negative V G to our devices, accessing both underdoped and overdoped regions of the phase diagram (Supplementary Note 3). At the outset, the intrinsic carrier concentration (1/qR H) as well as the sheet resistance R S and the Hall mobility μ H = R H/R S were measured for each sample. Table 1 shows these values along with the thickness, \(T_{{\mathrm{c}}_{{\mathrm{init}}}}\) (initial T c), \(T_{{\mathrm{c}}_{{\mathrm{min}}}}\) (minimum T c), T c(p opt) (T c at the optimal doping level) and variation in T c achieved through doping in each sample. In previous work, thin samples have been known to show higher R S and lower T c than thicker ones and superconductivity in 1 u.c. or thinner samples is only seen with graphene encapsulation20,21,22. Our unprotected 1 u.c. BSCCO-2212 devices are superconducting and we do not find a direct correlation between thickness and mobility leading us to conclude that the degree of disorder is the important parameter. This result can be attributed to our sample fabrication method13, 14 as well as the avoidance of lithography during device fabrication (Supplementary Note 4). We note that disorder can have significant impact on superconducting properties including T c suppression23,24,25, localization of Cooper pairs26 and broadening of the superconducting transition due to spatial inhomogeneity of the superconducting condensate27, 28.
Phase diagram
The R S(T) curves obtained at various doping levels depend on the electronic structure of the corresponding phase. Variations in the temperature dependence of R S have been successfully used to demarcate different regions of the cuprate phase diagram1, 2, 29. It is known that the normal state in the cuprates around optimal doping is characterized by a linear dependence of resistivity on temperature, generally called the “strange metal” phase. At higher doping and lower temperatures, this dependence assumes the normal metallic power law dependence in the “Fermi liquid” phase. At lower doping and lower temperatures, the dependence again deviates from linearity in a different manner in the region known as the “pseudo-gap” phase. The temperatures corresponding to deviations in linearity (Fig. 2a) can be used to determine the domain of existence of the different phases. It is to be seen if a single, coherent, doping vs. temperature phase diagram of BSCCO-2212 emerges from these measurements of devices with differing intrinsic disorder and T c.
Extraction of characteristic temperatures and parameters. a Sheet resistance as function of temperature of an underdoped device (overdoped in the inset). b Maximum T c of each device as a function of resistivity; T c(p opt) is the T c at the optimal doping level or the peak of the superconducting dome. c Dependence of the scaling factor Z on \(T_{\mathrm{c}}\left( {p_{{\mathrm{opt}}}} \right){\mathrm{/}}T_{{\mathrm{c}}_{{\mathrm{max}}}}\), where \(T_{{\mathrm{c}}_{{\mathrm{max}}}} = 84\) K is the maximum T c measured by us to date in 2D BSCCO-2212 devices. The black line is a fit to the data (black squares) of the measurements of Naqib et al. (Z ref.)3, while the magenta dots are the calculated values for the four devices of this work (Z exp.)
For each R S(T) curve, we use a linear fit for the “strange metal” high temperature region (290 K < T < 330 K) with \(\rho_{\square}(T) = \rho _{\mathrm{0}} + AT\), where ρ 0 is the residual square resistivity and A is the slope1. T m (temperature of crossover into the Fermi liquid phase) and T* (temperature of crossover into the pseudo-gap phase) are determined, respectively, as the temperature of upward and downward deviation (green curves) from the linear behavior (orange straight lines). Where possible, similar estimations were found for T m and T* by identifying the temperature at which dR s/dT deviates downward (upward) from its high temperature constant value (Supplementary Note 5). The downward deviation below T* in BSCCO-2212 is ascribed to the reduction of inelastic scattering rate of electrons in the pseudo-gap phase, when temperature is lowered30. This characteristic T* may however be different2 from the temperature of crossover into the pseudo-gap phase T pg, commonly detected by photo-emission, Raman, or tunneling spectroscopy17, 31, 32. It is well established in cuprates that in the Fermi liquid phase the upward deviation of R s(T) below T m follows the power law \(\rho_{\square}(T) = \rho _{\mathrm{0}} + BT^m\), where the exponent m is expected to increase with doping from 1 to 1.5–2 depending on the material3, 4, 33. In our overdoped devices, we observed an m(p) dependence3, with a maximum m = 1.35 at the doping level of 1.6 × 1015 cm−2 (~0.21 holes/Cu). The accessible range (up to 330 K) where linear behavior is found at high temperature ensures a reliable determination of T* and T m. The construction of the phase diagram for BSCCO-2212 also requires the determination of the carrier concentration for each device. We use two methods, the measured Hall coefficient (1/qR H) and an estimation of doped holes (p) per Cu atom (holes/Cu) obtained by an empirical and commonly used T c(p) relation34.
where T c(p opt) is the maximum critical temperature measured for each device corresponding to the optimal doping level and Z is a scale factor. In bulk material with minimal defects, Z is empirically determined to be 82.64, 35, 36 and superconductivity exists in the region p = 0.05 to p = 0.27 holes/Cu. Disorder reduces T c and constrains superconductivity to a smaller region in p 3 with a scaling of the superconducting dome. The lowering of T c due to disorder also corresponds to a higher normal state R S(T), ascribed both to Coulomb interactions and scattering by impurities23. In our 2D crystals, this behavior can be expected as shown qualitatively in Fig. 2b. The empirical relation for obtaining p from T c is modified in the presence of disorder3 by modifying the scaling parameter Z as shown in Fig. 2c. Thus characteristic temperatures are obtained as a function of doped holes/Cu allowing us to construct phase diagrams for our samples with varying intrinsic disorder.
Discussion
The resulting phase diagram with doping p determined from T c by Eq. (1) is shown in Fig. 3. The characteristic temperatures (T m and T*) and their dependence on p for the four devices establish remarkably coherent and well-demarcated domains corresponding to the well-known cuprate phase diagram. The superconducting dome, as determined from the empirical formula of Eq. (1), shrinks with increasing disorder as T c is suppressed, recalling the effect of a magnetic field37,38,39. We thus establish a complete phase diagram for ultra-thin BSCCO-2212 extending well into the underdoped and overdoped regions and explored entirely using electrostatic doping. In particular, we provide data in the overdoped region where scant information exists for BSCCO-221235, 40. The extracted phase boundary, notably between pseudogap region and the strange metal region, is not linear. Extrapolating this phase boundary to the doping axis would indicate a critical doping close to the optimal value, but higher values can be obtained by extrapolating segments of the phase boundary on the underdoped side. Finally, we construct the same phase diagram using carrier density estimated by 1/qR H (Fig. 4a) and reach two conclusions. First, the relation between p determined using Eq. (1) and 1/qR H is non-linear. This is confirmed in Fig. 4b where an exponential dependence is found between the two quantities16, 19 and in Fig. 4c where the horizontal 1/qR H axis is plotted in logarithmic scale yielding a result very similar to the phase diagram obtained in Fig. 3. However, we must keep in mind the limitations in the use of R H for estimating doping discussed above and note only the qualitative similarity between the phase diagrams of Figs 3 and 4c. Second, the data corresponding to the 2.5 u.c. device appears incoherent with the other devices while this was not the case in Fig. 3, where p is determined from the T c using Eq. (1). The probable reason is that in our 2.5 u.c. device the doping is not homogeneous over the total thickness given the small Thomas–Fermi screening length of cuprates (λ TF ~ 1 u.c.)8, 41 introducing an error in the determination of carrier density from 1/qR H. We conclude our analysis of R S(T) as a function of doping by examining the normal state behavior in greater detail. In the normal state, it has been shown that the slope A of the linear part of the R S(T) curve is inversely proportional to the doping with a simple, universal 1/p power law behavior1, 42. We confirm this finding as shown in Fig. 4d where we have accounted for the varying disorder in our devices by normalizing the measured slope A of the R S(T) curve by A N = \(A\mu _{\mathrm{H}}{\mathrm{/}}\mu _{H_{{\mathrm{max}}}}\), where μ H is the measured mobility of each device at T = 120 K and \(\mu _{{\mathrm{H}}_{{\mathrm{max}}}}\) is the highest measured mobility of our devices (in sample D, 1 u.c.).
Phase diagram of 2D space charge doped BSCCO-2212. Of the 32 measured RS(T) curves, 26 were of the quality needed for extracting characteristic temperatures. The characteristic temperatures T* (filled symbols), T m (open symbols), and T c (filled symbols on the domes) extracted for the four devices of this study are plotted as a function of doping (holes/Cu). They demarcate the boundaries of the pseudogap region (PG), the strange metal region (SM), the Fermi liquid region (FM), and the superconducting dome (SC). The different colors of the domes reflect the shrinking of the dome with disorder. The error on characteristic temperatures is estimated during their extraction while that on doping depends on T c through Eq. (1) and is significant around optimal doping. Where not shown, it is of the size of the data point or smaller
Phase diagram with carrier density inferred from R H. a Characteristic temperatures as in Fig. 3 with T* (filled symbols), T m (open symbols) and (filled symbols below 100 K) of the four devices as a function of 1/qR H, and the resulting phase diagram. b Doping calibration: Exponential dependence of 1/qR H on the calculated holes/Cu. c Same as a but accounting for the exponential functional dependence found in b. The vertical green band indicates the region of optimal doping. Though limitations in the use of R H for estimating doping preclude quantitative conclusions, a qualitative similarity with Fig. 3 can be seen. d Doping dependence of normalized slope A N of the linear part of R S(T) in the strange metal phase (T > T*, T m). A N values for the four devices fall on a single curve (solid line) given by A N ∝ −b × ln(holes/Cu). Inset: doping dependence of the slope A before normalization. Error bars in a–c take into account uncertainty of determination of characteristic temperatures and R H
While the superconducting transition is by definition abrupt, in 2D systems a smooth transition occurs whose nature is thought to belong to the Kosterlitz–Thouless (KT) class43,44,45,46 and which is characterized by the temperature T KT above which superfluid density discontinuously attains zero47, 48. Such a transition is difficult to observe experimentally because of competing phenomena such as disorder27 and finite-size effects49, which broaden the superconducting transition for T < T KT. These factors induce spatial inhomogeneities of the superconducting condensate on the mesoscopic scale50 affecting critical temperatures and the superconducting gap51. Though an in-depth analysis of the influence of dimensionality, disorder and doping is beyond the scope of this work, we probe below the variation of the superconducting transition width as a function of doping.
In Fig. 5a, the superconducting transition from the underdoped to the overdoped region is shown for device C (1.5 u.c.). A strong reduction of the transition width with doping is clearly visible. Since doping affects both the superconducting transition width and the normal state behavior, we first normalize each R S(T) curve by R N(T), its normal state component, fitted by R N(0) + BT m in the overdoped region, or by R N(0) + aT − bT 2 in the underdoped region. To estimate an intrinsic superconducting transition width, we must eliminate extrinsic contributions (e.g., from disorder), which tend to broaden the transition either at the onset or near T c. This is done using the normalized R S(T)/R N(T) curves by fitting a linear component to the transition and extracting two limiting temperatures T h and T l, corresponding to the “intrinsic” onset and critical temperature as shown in Fig. 5b. The transition width normalized to the critical temperature is then approximated as ΔT/T c ≈ (T h − T l)/T l. In conventional 2D superconductors, \({\mathrm{\Delta }}T{\mathrm{/}}T_{\mathrm{c}} \simeq \left( {\alpha _{\mathrm{0}}{\mathrm{/}}\xi } \right)^2\) (where α 0 is the inter-atomic distance and ξ the coherence length) is of the order of 0.02 and the broadening of the superconducting transition is ascribed to Aslamazov–Larkin fluctuations28. Fluctuation phenomena are prominent in cuprates due to the short coherence length and ΔT/T c is expected to be higher. In Fig. 5b, we show the variation of ΔT/T c for each device as a function of doping p. It is significantly higher than for a conventional 2D superconductor and decreases strongly with doping in the underdoped region. We remark that devices A (2.5 u.c.) and C (1.5 u.c.) have a higher ΔT/T c. Device C (1.5 u.c.) has the lowest mobility and is probably the most disordered while the thickest device A (2.5 u.c.) can be expected to have a gradient in the doping over the total thickness (Supplementary Note 6). Thus extrinsic factors like disorder and inhomogeneity can lead to an increased ΔT/T c. However, in all devices ΔT/T c decreases strongly with doping until the optimal doping is attained and then remains almost unchanged. This can be ascribed to a change in the inhomogeneity landscape49, 52, which in turn increases the characteristic dimension of homogeneous superconducting domains and the spatial coherence of the superconducting state. Electronic correlations are also reduced as carrier density and coherence increase.
Transition width dependence on electrostatic doping. a R S(T) of device C (1.5 u.c.), normalized to R S(120 K). Thick lines indicate the most underdoped (UD, blue), the optimally doped (OP, green), and the most overdoped (OD, brown) curves. b R S(T)/R N(T) (with R N(T) normal state resistance) in the proximity of the superconducting transition. R N(T) is determined as R 0 + BT m or as R 0 + aT − bT 2 according to whether the device is overdoped or underdoped, respectively. A linear component is fitted to the superconducting transition with T h and T l extrapolated as the intersection with the dashed green line and the x axis, respectively. c Doping dependence of the normalized superconducting transition width ΔT/T c, for varying thickness and disorder. Error bars take into account uncertainty of determination of transition width
In conclusion, we fabricate ultra-thin, superconducting (1–2.5 unit cell) BSCCO-2212 devices to which we apply a highly efficient electrostatic doping technique called space charge doping. Starting from the nominal optimal doping, we obtain carrier density variations of the order of 1015 cm−2, as estimated by Hall measurements, both in the overdoped and in the underdoped regions, entirely through space charge doping. We measure sheet resistance as a function of doping from 330 K to well below the superconducting transition. From these measurements, we extract characteristic temperatures demarcating the various regions of the phase diagram. These measurements allow us to construct a comprehensive phase diagram as a function of doping, temperature, and disorder in 2D Bi2Sr2CaCu2O8+x and to analyze the influence of doping, disorder, and two dimensionality. The variation of normal state characteristics of the sheet resistance as well as the variation of the superconducting transition width is traced continually as a function of doping. Our results demonstrate the potential of space charge doping in 2D crystals to develop the fundamental understanding of phase transitions in these materials as well as possible applications.
Methods
Sample preparation
Few-nm BSCCO-2212 samples were made by the anodic bonding method13, 14. Bi2Sr2CaCu2O8+x flakes were peeled off from bulk crystals and deposited on a 0.5 mm-thick soda-lime glass substrate with 1 nm roughness according to AFM topography measurements. Substrate and precursor were subsequently placed between two electrodes and heated between 150 and 200 °C in order to activate Na+ mobility within the glass. High negative voltage was then applied to the face of the glass opposite of the sample to attract Na+ ions, thus creating an O2− space charge at the glass–sample interface. After 5–10 min, the precursor is electrostatically bonded to the glass and the voltage can be removed. This electrostatic bond involves the first few nm of the precursor, and using adhesive tape, the upper layers can be mechanically exfoliated, leaving large area ultra-thin BSCCO-2212 on the glass substrate. The thickness of the samples were evaluated by AFM measurements and optical contrast.
Measurements details
Electrical contacts were made in Van der Pauw geometries by depositing 100 nm Au in a standard thermal evaporator at the pressure of 10−6 mbar. The backside of the glass substrate was then glued by silver epoxy to a gold electrode evaporated on top of an insulating MgO substrate to act as a back gate. Four point resistivity and Hall measurements were made in a high vacuum (10−6 mbar) Oxford He-flow cryostat with a minimum temperature of 2.8 K and maximum 420 K. A resistive electromagnet was used to apply magnetic fields up to 2 T perpendicular to the sample.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
References
Barisic, N. et al. Universal sheet resistance and revised phase diagram of the cuprate high-temperature superconductors. Proc. Natl. Acad. Sci. 110, 12235–12240 (2013).
Ando, Y., Komiya, S., Segawa, K., Ono, S. & Kurita, Y. Electronic phase diagram of high-T c cuprate superconductors from a mapping of the in-plane resistivity curvature. Phys. Rev. Lett. 93, 267001 (2004).
Naqib, S., Cooper, J., Tallon, J. & Panagopoulos, C. Temperature dependence of electrical resistivity of high-T c cuprates–from pseudogap to overdoped regions. Phys. C Supercond. 387, 365–372 (2003).
Konstantinović, Z., Li, Z. & Raffy, H. Evolution of the resistivity of single-layer Bi2Sr1.6La0.4CuO y thin films with doping and phase diagram. Phys. C Supercond. 351, 163–168 (2001).
Yuan, H. et al. High-density carrier accumulation in ZnO field-effect transistors gated by electric double layers of ionic liquids. Adv. Funct. Mater. 19, 1046–1053 (2009).
Ye, J. T. et al. Liquid-gated interface superconductivity on an atomically flat film. Nat. Mater. 9, 125–128 (2010).
Parendo, K. A. et al. Electrostatic tuning of the superconductor-insulator transition in two dimensions. Phys. Rev. Lett. 94, 197004 (2005).
Bollinger, A. T. et al. Superconductor–insulator transition in La2−x Sr x CuO4 at the pair quantum resistance. Nature 472, 458–460 (2011).
Leng, X., Garcia-Barriocanal, J., Bose, S., Lee, Y. & Goldman, A. M. Electrostatic control of the evolution from a superconducting phase to an insulating phase in ultrathin YBa2Cu3O7−x films. Phys. Rev. Lett. 107, 027001 (2011).
Crassous, A. et al. Nanoscale electrostatic manipulation of magnetic flux quanta in ferroelectric/superconductor BiFeO3/YBa2Cu3O7−δ heterostructures. Phys. Rev. Lett. 107, 247002 (2011).
Biscaras, J., Chen, Z., Paradisi, A. & Shukla, A. Onset of two-dimensional superconductivity in space charge doped few-layer molybdenum disulfide. Nat. Commun. 6, 8826 (2015).
Paradisi, A., Biscaras, J. & Shukla, A. Space charge induced electrostatic doping of two-dimensional materials: graphene as a case study. Appl. Phys. Lett. 107, 143103 (2015).
Shukla, A., Kumar, R., Mazher, J. & Balan, A. Graphene made easy: high quality, large-area samples. Solid State Commun. 149, 718–721 (2009).
Balan, A. et al. Anodic bonded graphene. J. Phys. D Appl. Phys. 43, 374013 (2010).
Ando, Y., Kurita, Y., Komiya, S., Ono, S. & Segawa, K. Evolution of the hall coefficient and the peculiar electronic structure of the cuprate superconductors. Phys. Rev. Lett. 92, 197001 (2004).
Bouvier, J. & Bok, J. Electron-phonon interaction in the high- cuprates in the framework of the Van Hove scenario. Adv. Condens. Matter Phys. 2010, 472636 (2010).
Benhabib, S. et al. Collapse of the normal-state pseudogap at a Lifshitz transition in the Bi2Sr2CaCu2O8+δ . Phys. Rev. Lett. 114, 147001 (2015).
Bok, J. & Bouvier, J. Hall effect in the normal state of high-T c cuprates. Phys. C Supercond. 408–410, 242–243 (2004).
Uemura, T. et al. Temperature dependence of the Hall effect in pentacene field-effect transistors: possibility of charge decoherence induced by molecular fluctuations. Phys. Rev. B 85, 035313 (2012).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 102, 10451–10453 (2005).
Jiang, D. et al. High-T c superconductivity in ultrathin Bi2Sr2CaCu2O8+x down to half-unit-cell thickness by protection with graphene. Nat. Commun. 5, 5708 (2014).
You, L. X., Yurgens, A., Winkler, D., Lin, C. T. & Liang, B. Superconducting properties of ultrathin Bi2Sr2CaCu2O8+x single crystals. J. Appl. Phys. 98, 033913 (2005).
Finkel’shtein, A. M. Superconducting transition temperatures of ultrathin amorphous films. Sov. Phys. JETP Lett. 45, 46–49 (1987).
Haviland, D. B., Liu, Y. & Goldman, A. M. Onset of superconductivity in the two-dimensional limit. Phys. Rev. Lett. 62, 2180–2183 (1989).
Norton, D. P., Lowndes, D. H., Pennycook, S. J. & Budai, J. D. Depression and broadening of the superconducting transition in superlattices Based on YBa2Cu3O7−δ: influence of the barrier layers. Phys. Rev. Lett. 67, 1358–1361 (1991).
Bouadim, K., Loh, Y. L., Randeria, M. & Trivedi, N. Single- and two-particle energy gaps across the disorder-driven superconductor–insulator transition. Nat. Phys. 7, 884–889 (2011).
Benfatto, L., Castellani, C. & Giamarchi, T. Broadening of the Berezinskii-Kosterlitz-Thouless superconducting transition by inhomogeneity and finite-size effects. Phys. Rev. B 80, 214506 (2009).
Caprara, S., Grilli, M., Benfatto, L. & Castellani, C. Effective medium theory for superconducting layers: a systematic analysis including space correlation effects. Phys. Rev. B 84, 014514 (2011).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Daou, R. et al. Linear temperature dependence of resistivity and change in the Fermi surface at the pseudogap critical point of a high-T c superconductor. Nat. Phys. 5, 31–34 (2009).
Kordyuk, A. A. Pseudogap from ARPES experiment: three gaps in cuprates and topological superconductivity (Review Article). Low Temp. Phys. 41, 319–341 (2015).
Fischer, Ø., Kugler, M., Maggio-Aprile, I., Berthod, C. & Renner, C. Scanning tunneling spectroscopy of high-temperature superconductors. Rev. Mod. Phys. 79, 353–419 (2007).
Kubo, Y., Shimakawa, Y., Manako, T. & Igarashi, H. Transport and magnetic properties of Tl2Ba2CuO6+δ showing a δ-dependent gradual transition from an 85-K superconductor to a nonsuperconducting metal. Phys. Rev. B 43, 7875–7882 (1991).
Presland, M., Tallon, J., Buckley, R., Liu, R. & Flower, N. General trends in oxygen stoichiometry effects on T c in Bi and Tl superconductors. Phys. C Supercond. 176, 95–105 (1991).
Raffy, H., Toma, V., Murrills, C. & Li, Z. Z. c-axis resistivity of Bi2Sr2CaCu2O y thin films at various oxygen doping: phase diagram and scaling law. Phys. C Supercond. 460–462, 851–853 (2007).
Leng, X. et al. Indications of an electronic phase transition in two-dimensional superconducting YBa2Cu3O7−x thin films induced by electrostatic doping. Phys. Rev. Lett. 108, 067004 (2012).
Ando, Y. et al. Resistive upper critical fields and irreversibility lines of optimally doped high-T c cuprates. Phys. Rev. B 60, 12475–12479 (1999).
Xiaowen, C., Zhihe, W. & Xiaojun, X. Magnetoresistance and a crossover from activated to diffusive dissipation in the mixed state for YBa2Cu2O7−δ epitaxial thin films. Phys. Rev. B 65, 064521 (2002).
Carrington, A., Walker, D. J. C., Mackenzie, A. P. & Cooper, J. R. Hall effect and resistivity of oxygen-deficient YBa2Cu3O7−x . Phys. Rev. B 48, 13051–13059 (1993).
Konstantinovic, Z., Li, Z. & Raffy, H. Normal state transport properties of single- and double-layered Bi2Sr2Ca n−1Cu n O y thin films and the pseudogap effect. Phys. C Supercond. 341–348, 859–862 (2000).
Smadici, S. et al. Superconducting transition at 38 K in insulating- overdoped La2CuO4-La1.64Sr0.36CuO4. Phys. Rev. Lett. 102, 107004 (2009).
Watanabe, T., Fujii, T. & Matsuda, A. Anisotropic resistivities of precisely oxygen controlled single-crystal Bi2Sr2CaCu2O8+δ : systematic study on “spin gap” effect. Phys. Rev. Lett. 79, 2113–2116 (1997).
Artemenko, S., Gorlova, I. & Latyshev, Y. Vortex motion and kosterlitz-thouless transition in superconducting single crystals Bi2Sr2CaCu2O x . Phys. Lett. A 138, 428–434 (1989).
Martin, S., Fiory, A. T., Fleming, R. M., Espinosa, G. P. & Cooper, A. S. Vortex-pair excitation near the superconducting transition of Bi2Sr2CaCu2O8+δ crystals. Phys. Rev. Lett. 62, 677–680 (1989).
Pradhan, A. K. et al. Observation of the Kosterlitz-Thouless transition and of vortex fluctuations in superconducting single crystals of Bi-based cuprates. Phys. Rev. B 47, 11374–11378 (1993).
Yong, J. et al. Evidence of two-dimensional quantum critical behavior in the superfluid density of extremely underdoped Bi2Sr2CaCu2O8+δ . Phys. Rev. B 85, 180507 (2012).
Kosterlitz, J. M. & Thouless, D. J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 6, 1181–1203 (1973).
Halperin, B. I. & Nelson, D. R. Resistive transition in superconducting films. J. Low Temp. Phys. 36, 599–616 (1979).
Schneider, T. & Weyeneth, S. Suppression of the Berezinskii-Kosterlitz-Thouless and quantum phase transitions in two-dimensional superconductors by finite-size effects. Phys. Rev. B 90, 064501 (2014).
Gomes, K. K. et al. Visualizing pair formation on the atomic scale in the high-T c superconductor Bi2Sr2CaCu2O8+δ . Nature 447, 569–572 (2007).
Sacépé, B. et al. Disorder-Induced Inhomogeneities of the superconducting state close to the superconductor-insulator transition. Phys. Rev. Lett. 101, 157006 (2008).
Schneider, T., Caviglia, A. D., Gariglio, S., Reyren, N. & Triscone, J.-M. Electrostatically-tuned superconductor-metal-insulator quantum transition at the LaAlO3/SrTiO3 interface. Phys. Rev. B 79, 184502 (2009).
Acknowledgements
We thank the Institut des NanoSciences de Paris for access to the electromagnet facility. We acknowledge the Consortium des salles blanches d’Ile de France, M. Rosticher and J. Palomo for access to clean room facilities. This work was supported by French state funds managed by the ANR within the Investissements d’Avenir programme under reference ANR-11-IDEX-0004-02 and more specifically within the framework of the Cluster of Excellence MATISSE led by Sorbonne Universités.
Author information
Authors and Affiliations
Contributions
A.S. designed the project. A.E. synthesized the BSCCO single crystal precursors, E.S. fabricated the devices, performed the measurements with J.B. and analyzed the data. E.S., J.B., and A.S. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sterpetti, E., Biscaras, J., Erb, A. et al. Comprehensive phase diagram of two-dimensional space charge doped Bi2Sr2CaCu2O8+x . Nat Commun 8, 2060 (2017). https://doi.org/10.1038/s41467-017-02104-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-017-02104-z
This article is cited by
-
High-temperature Josephson diode
Nature Materials (2024)
-
Single-photon detection using high-temperature superconductors
Nature Nanotechnology (2023)
-
Prominent Josephson tunneling between twisted single copper oxide planes of Bi2Sr2-xLaxCuO6+y
Nature Communications (2023)
-
Superior carrier tuning in ultrathin superconducting materials by electric-field gating
Nature Reviews Physics (2022)
-
Indium-contacted van der Waals gap tunneling spectroscopy for van der Waals layered materials
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.