pKWmEB: integration of Kruskal–Wallis test with empirical Bayes under polygenic background control for multi-locus genome-wide association study

Abstract

Although nonparametric methods in genome-wide association studies (GWAS) are robust in quantitative trait nucleotide (QTN) detection, the absence of polygenic background control in single-marker association in genome-wide scans results in a high false positive rate. To overcome this issue, we proposed an integrated nonparametric method for multi-locus GWAS. First, a new model transformation was used to whiten the covariance matrix of polygenic matrix K and environmental noise. Using the transferred model, Kruskal–Wallis test along with least angle regression was then used to select all the markers that were potentially associated with the trait. Finally, all the selected markers were placed into multi-locus model, these effects were estimated by empirical Bayes, and all the nonzero effects were further identified by a likelihood ratio test for true QTN detection. This method, named pKWmEB, was validated by a series of Monte Carlo simulation studies. As a result, pKWmEB effectively controlled false positive rate, although a less stringent significance criterion was adopted. More importantly, pKWmEB retained the high power of Kruskal–Wallis test, and provided QTN effect estimates. To further validate pKWmEB, we re-analyzed four flowering time related traits in Arabidopsis thaliana, and detected some previously reported genes that were not identified by the other methods.

Introduction

The genome-wide association study (GWAS) has become a very effective approach to identifying the genetic loci associated with complex traits (Sladek et al. 2007; WTCCC 2007; Li et al. 2013). Since the establishment of mixed linear model (MLM) based GWAS methods (Zhang et al. 2005; Yu et al. 2006), then there has been an increasing interest in using MLM in GWAS, because of their demonstrated effectiveness in accounting for relatedness between individuals and in controlling population stratification. This has stimulated the development of the MLM-based GWAS methods (Kang et al. 2008; Zhang et al. 2010; Lippert et al. 2011; Zhou and Stephens 2012; Segura et al. 2012; Wang et al. 2016). Furthermore, these methods have been widely used in GWAS; the loci identified in GWAS explain only a fraction of heritability of complex trait, indicating that additional loci influencing those traits exist.

To increase the robustness of quantitative trait nucleotide (QTN) detection in GWAS, nonparametric approaches have been recommended. Up to now several existing nonparametric methods have been used to conduct GWAS. For example, Atwell et al. (2010) adopted Wilcoxon rank-sum test (Wilcoxon 1945; Mann and Whitney 1947) to carry out GWAS for 107 phenotypes in a common set of Arabidopsis thaliana inbred lines; the 107 phenotypes were re-analyzed by Kruskal–Wallis test (Kruskal and Wallis 1952) and more significantly associated SNPs were identified as compared with those using efficient mixed model association (EMMA) (Filiault and Maloof 2012); the Kruskal–Wallis test was also generalized to group uncertainty when comparing k samples, and one application to a GWAS of type 1 diabetic complications demonstrated the utility of the generalized Kruskal–Wallis test for study with group uncertainty (Acar and Sun 2013). Similarly, Beló et al. (2008) used Kolmogorov–Smirnov test (Kolmogorov 1933; Smirnov 1948) to detect an allelic variant of fad2 associated with increased oleic acid levels in maize, and Terao et al. (2014) and Tan et al. (2014) adopted Jonckheere–Terpstra test (Terpstra 1952; Jonckheere 1954) to detect a T allele of rs2395185 in human leukocyte antigen locus and a T allele of rs1260326 and rs780094 in glucokinase regulatory loci, respectively. None of the above approaches have included population structure in their genetic model. Thus, Yang et al. (2014) integrated Anderson–Darling test with a population structure correction. This method was used to analyze 17 agronomic traits in maize, and some important loci were identified. In practice, the true model for a quantitative trait is rarely known, and model misspecification can lead to a loss of power. To address this issue, Kozlitina and Schucany (2015) proposed a rank-based maximum test (MAX3), which has favorable properties relative to other tests, especially in the case of symmetric distributions with heavy tails. We found that all the above methods have high false positive rates (FPRs) in our simulation experiments. To overcome this problem, multi-locus model methodologies should be recommended. For example, Li et al. (2014) proposed a two-stage nonparametric approach, in which all the markers potentially associated with quantitative trait are identified and their effects in one multi-locus model are estimated by shrinkage estimation for true QTN detection. However, none of the above methods have controlled polygenic background in single-marker association in genome scans.

In this study, we proposed a two-stage method for multi-locus GWAS. First, the model transformation of Wen et al. (2017) was used to control polygenic background in single-marker association in genome scans. Using the transformed model, Kruskal–Wallis test along with least angle regression (LARS) of Efron et al. (2004) was then used to select all the markers that were potentially associated with the trait. Finally, all the selected markers were placed into multi-locus model, these effects were estimated by empirical Bayes, and all the nonzero effects were further identified by a likelihood ratio test. Clearly, this method integrates the Kruskal–Wallis test with empirical Bayes under polygenic background control. This method, named pKWmEB, was validated by a series of Monte Carlo simulation studies and real data analyses for four flowering time related traits in Arabidopsis.

Materials and methods

The Arabidopsis thaliana data set

The Arabidopsis thaliana data set was downloaded from http://www.arabidopsis.usc.edu/ (Atwell et al. 2010) and used to conduct simulation experiments and real data analysis. This data set contained 199 accessions each with 216130 genotyped SNPs.

Genetic model and model transformation

The standard MLM for an n × 1 phenotypic vector y of quantitative trait is

$${\mathbf{y}} = {\bf{1}}{\it{\mu }}{\bf{ + Qv}} + {\bf{G}}\beta + {\mathbf{Zu}} + {\mathrm{\varepsilon }}$$

(1)

where n is the number of individuals; 1 is a n × 1 vector of 1; μ is overall average; Q is an n × c matrix of fixed effects, including population structure (Yu et al. 2006) or principle component (Price et al. 2010), and v is a c × 1 vector of fixed effects excluding the intercept μ; G is an n × 1 vector of putative QTN genotypes, and β is fixed effect of putative QTN; ${\mathbf{u}}\sim {\mathrm{MVN}}_m({\mathbf{0}},\sigma _g^2{\mathbf{K}})$ is an m × 1 vector of polygenic effects, K is an m × m kinship matrix, $\sigma _g^2$ is polygenic variance, and MVN denotes multivariate normal distribution; Z = (z_ij)_n × m is the corresponding designed matrix for u, z_ij = 1 if individual i comes from family j (j = 1, …, m) and z_ij = 0 otherwise; and ${\mathrm{\varepsilon \sim }}{\mathrm{MVN}}_n({\mathbf{0}},\sigma _e^2{\mathbf{I}}_n)$ is an n × 1 vector of residual errors, $\sigma _e^2$ is residual error variance, I_n is an n × n identity matrix. To simplify population structure, let m = n and Z = I_n in this study (Atwell et al. 2010). Note that the observed data is (y, G), matrices Q and K can be calculated from G, and the parameters to be estimated are μ, v, β, $\sigma _g^2$ and $\sigma _e^2$.

Based on model (1), phenotypic values y were affected by population structure, QTN and polygenes. In other words, a nonparametric test for k samples cannot be directly applied. Thus, we must remove the effects for population structure and polygenes before using a nonparametric test.

Population structure correction

If we delete Gβ and Zu in model (1), its reduced model is

$${\mathbf{y}} = {\bf{1}}{\it{\mu }}{\bf{ + Qv}} + {\mathrm{\varepsilon }}$$

(2)

Using least squares method, the effect of v, denoted by $\hat{\bf v}$, can be estimated from y, Q and 1. Thus, we can correct the effect of population structure from

$${\mathbf{y}}_{{\mathrm{ - }}Q} = {\mathbf{y}} - {\bf Q}\hat{\bf v} = {\bf{1}}{\it{\mu }}{\bf{ + G}}\beta + {\mathbf{Zu}} + {\mathrm{\varepsilon }}$$

(3)

Polygenic background correction

Based on model (3), the variance of y_−Q is

$$\begin{array}{c}{\rm{ Var }}\left( {{\mathbf{y}}_{{\mathrm{ - }}Q}} \right) = \sigma _g^2{\mathbf{ZKZ}}^T + \sigma _e^2{\mathbf{I}}_n\\ = \sigma _e^2\left( {\lambda _g{\mathbf{ZKZ}}^T + {\mathbf{I}}_n} \right)\end{array}$$

(4)

where $\lambda _g = \sigma _g^2/\sigma _e^2$. Using the EMMA algorithm of Kang et al. (2008), the estimate of λ_g, denoted by $\hat \lambda _g$, can be easily obtained. Replacing λ_g in (4) by $\hat \lambda _g$, so

$${\mathrm{Var}}\left( {{\mathbf{y}}_{{\mathrm{ - }}Q}} \right) = \sigma _e^2\left( {\hat \lambda _g{\mathbf{ZKZ}}^{\rm T} + {\mathbf{I}}_n} \right) = \sigma _e^2{\mathbf{B}}$$

(5)

where ${\mathbf{B}} = \hat \lambda _g{\mathbf{ZKZ}}^{\rm T} + {\mathbf{I}}_n$. An eigen decomposition of positive semi-definite matrix B is

$$\begin{array}{c}{\mathbf{B}} = {\mathbf{Q}}_B{\mathbf{\Lambda}}_B{\mathbf{Q}}_B^{\rm{T}}\\ = \left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1} & {{\mathbf{Q}}_2} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{\Lambda }}_r} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1^{\rm{T}}} \\ {{\mathbf{Q}}_2^{\rm{T}}} \end{array}} \right)\\ = \left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1} & {{\mathbf{Q}}_2} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1^T} \\ {{\mathbf{Q}}_2^{\rm{T}}} \end{array}} \right)\\ = \left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1} & {{\mathbf{Q}}_2} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1^T} \\ {{\mathbf{Q}}_2^T} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1} & {{\mathbf{Q}}_2} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathbf{Q}}_1^T} \\ {{\mathbf{Q}}_2^T} \end{array}} \right)\\ = \left( {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^T} \right)\left( {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^T} \right)\end{array}$$

(6)

where Q_B is orthogonal, Λ_r is a diagonal matrix with positive eigen values, r = Rank(B), Q₁ and Q₂ are the n × r and n × (n − r) block matrices of Q_B, and 0 is the corresponding block zero matrix (Wen et al. 2017).

Let ${\mathbf{C}} = {\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{ - \begin{array}{*{20}{c}} {} \end{array}{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}$, a new model with polygenic background control is

$${\mathbf{y}}_c = {\bf{1}}_c{\it{\mu }} + {\bf{G}}_c\beta + {\mathrm{\varepsilon }}_c$$

(7)

where y_c = Cy_−Q, 1_c = C1, G_c = CG and ε_c = C(Zu + ε). Clearly, the observed data is (y_c,G_c), and the parameter to be estimated is β. Using $\lambda _g = \hat \lambda _g$, equation (6) and ${\mathbf{Q}}_1^{\rm T}{\mathbf{Q}}_1 = {\mathbf{I}}_r$, so

$$\begin{array}{c}{\rm Var}\left( {{\mathbf{\varepsilon }}_c} \right) = \sigma _e^2{\mathbf{C}}\left( {\hat \lambda _g{\mathbf{ZKZ}}^{\rm T} + {\mathbf{I}}_n} \right){\mathbf{C}}^{\rm T}\\ = \sigma _e^2{\mathbf{CBC}}^{\rm T}\\ = \sigma _e^2\left[ {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\begin{array}{*{20}{c}} - \end{array}{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}\left( {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}} \right)\left( {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}} \right)\left( {{\mathbf{Q}}_1{\mathbf{\Lambda }}_r^{\begin{array}{*{20}{c}} - \end{array}{\textstyle{1 \over 2}}}{\mathbf{Q}}_1^{\rm T}} \right)^{\rm T}} \right]\\ = \sigma _e^2{\mathbf{I}}_n\end{array}$$

It should be noted that model (7) includes QTN variation and normal residual error (Wen et al. 2017). Although the polygenic background has been corrected, nonparametric test cannot be implemented owing to continual G_c values.

Kruskal–Wallis test

Based on model (7), we used Kruskal–Wallis test to detect whether one SNP was associated with the trait. However, the values of G_c were not binary variable. Thus, we must transfer G_c into binary variable. Let G_c = (g_ij)_n × p, ${\bf{G}}_c^*{\mathrm{ = }}\left( {g_{ij}^*} \right)_{n \times p}$, p is the number of QTNs under study and $\bar g_{ \cdot j} = \frac{1}{n}\mathop {\sum}\nolimits_{i = 1}^n {g_{ij}}$, so

$$g_{ij}^*{\mathrm{ = }}\left\{ {\begin{array}{*{20}{c}} {1,\;g_{ij} \ge \bar g_{ \cdot j}} \\ { - 1,\;g_{ij} < \bar g_{ \cdot j}} \end{array}} \right.$$

(8)

Therefore, $\left( {{\mathbf{y}}_c,{\bf{G}}_c^*} \right)$ is the data set for Kruskal–Wallis test. All the transferred phenotypes y_c were grouped by the values of ${\bf{G}}_c^*$. In this situation, there are two groups for the transferred phenotypes y_c. In the two groups, let their sizes be n_i, and their cumulative distribution functions be F_i(y|θ_i) (i = 1, 2). The null hypothesis for Kruskal–Wallis test was

$${\mathrm{H}}_0:\theta _1 = \theta _2{\mathrm{;}}\;{\mathrm{H}}_1:\theta _1 \ne \theta _2$$

(9)

When precise category assignment of ${\bf{G}}_c^*$ is available, Kruskal–Wallis test for equation (9) is conducted by ranking all the transferred phenotypes y_c together and comparing the rank sum for each group. If H₀:θ₁ = θ₂, so the estimate for β in equation (7) equals to zero. The statistic H

$$H = \frac{{12}}{{n\left( {n + 1} \right)}}\mathop {\sum}\limits_{i = 1}^2 {\frac{{R_i^2}}{{n_i}}} - 3\left( {n + 1} \right)$$

(10)

follows an asymptotic χ² distribution with one degree of freedom (Kruskal 1952), where r_j is the rank of the jth phenotype of y_c in the overall sample; and $R_i = \mathop {\sum}\limits_{j = 1}^n {I_{ij}} r_j$ (i = 1, 2), I_ij is an indicator variable, I_ij = 1 if the jth phenotype of y_c belongs to the ith group and I_ij = 0 otherwise; and $n_i = \mathop {\sum}\limits_{j = 1}^n {I_{ij}}$.

Empirical Bayes estimation for QTN effects

In GWAS, the number of SNPs is frequently 1000 times larger than sample size. In this situation, fitting all the genome markers in one model is not feasible. As we know, most SNPs are not associated with the trait. Once we delete these SNPs with zero effects, the reduced model is estimable. The purpose of the above Kruskal–Wallis test is to select all the potentially associated SNPs. If the number of markers passing the 0.05 level of significance test is more than o_i (o_i = 50, 100, and 150), we invoke LARS of Efron et al. (2004) to select o_i variables that are most likely associated with the trait of interest. LARS is a flexible method for variable selection, which is implemented by lars package in R language (http://cran.r-project.org/web/packages/lars/). The o_i markers are then included in a multi-locus model. If the number of markers passing the initial test is less than o_i, we skip the LARS step and proceed to include all the selected markers in a multi-locus model

$${\mathbf{y}} = {\bf{1}}{\it{\mu }} + \mathop {\sum}\limits_{i = 1}^q {{\mathbf{G}}_i{\it{\beta }}_i} + {\mathrm{\varepsilon }}$$

(11)

where y, 1, μ, and ε are the same as those in model (1); q is the number of markers selected in Krusal–Wallis test; β_i is the effect for marker i, and G_i is the corresponding designed matrix for β_i. Clearly, the observed data is (y, G₁, …,G_q), the parameters to be estimated are β₁,…,β_q. In model (11), the polygenic background is not considered. In theory, this is because all the potentially associated loci have been included in this model. However, we should determine whether population structure is considered. To solve this issue, the linkage disequilibrium score regression test of Bulik-Sullivan et al. (2015) is used (see Discussion). In the selection of markers, a less stringent criterion is adopted.

Empirical Bayes of Xu (2010) was used to estimate the SNP effects in model (11). In this method, each SNP effect β_i is viewed as random. We adopt normal prior for β_i, $P(\beta _i|\sigma _i^2){\mathrm{ = }}N\left( {0,\sigma _i^2} \right)$, and the scaled inverse χ² prior for $\sigma _i^2$, $P(\sigma _i^2|\tau ,\omega ) \propto \left( {\sigma _i^2} \right)^{{\mathrm{ - }}{\textstyle{1 \over 2}}\left( {\tau + 2} \right)}\exp \left( { - \frac{\omega }{{2\sigma _i^2}}} \right)$, where (τ,ω) = (0,0), which represents the Jeffreys’ prior (Figueiredo 2003), $P\left( {\sigma _i^2|\tau ,\omega } \right){\mathrm{ = 1/}}\sigma _i^2$. The procedure for parameter estimation in empirical Bayes is as follows.

• 1. Initial-step: To initialize parameters with

  $$\begin{array}{l}\mu = {\bf{1}}^{\rm T}{\mathbf{y}}/n\\ \sigma _e^2 = \frac{1}{n}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)^{\rm T}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)\\ \sigma _i^2 = \left[ {\left( {{\mathbf{G}}_i^{\rm T}{\mathbf{G}}_i} \right)^{{\mathrm{ - }}1}{\mathbf{G}}_i^{\rm T}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)} \right]^2 + \left( {{\mathbf{G}}_i^{\rm T}{\mathbf{G}}_i} \right)^{{\mathrm{ - }}1}\sigma _e^2\end{array}$$

• 2. E-step: marker effect can be predicted by

  $$E\left( {\beta _i} \right) = \sigma _i^2{\mathbf{G}}_i^{\rm T}{\bf{V}}^{ - 1}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)$$

  (12)

  where ${\bf{V}} = \mathop {\sum}\limits_{i = 1}^q {{\mathbf{G}}_i^{}} {\mathbf{G}}_i^{\rm T}\sigma _i^2 + {\bf{I}}\sigma _e^2$.

• 3. M-step: To update parameters $\sigma _i^2$, μ and $\sigma _e^2$

$$\begin{array}{l}\sigma _i^2{\mathrm{ = }}\frac{{E\left( {\beta _i^{\rm T}\beta _i} \right) + \omega }}{{\tau {\mathrm{ + 3}}}}\\ \mu = \left( {{\bf{1}}^{\rm T}{\bf{V}}^{ - 1}{\bf{1}}} \right)^ - {\bf{1}}^{\rm T}{\bf{V}}^{ - 1}{\mathbf{y}}\\ \sigma _e^2 = \frac{1}{n}\left( {{\mathbf{y}} - {\bf{1}}\mu } \right)^{\rm T}\left( {{\mathbf{y}} - {\bf{1}}\mu - \mathop {\sum}\limits_{i = 1}^q {{\mathbf{G}}_iE\left( {\beta _i} \right)} } \right)\end{array}$$

(13)

where $E\left( {\beta _i^T\beta _i} \right)$ $= E\left( {\beta _i^T} \right)E\left( {\beta _i} \right) + tr\left[ {var\left( {\beta _i} \right)} \right]$, $var\left( {\beta _i} \right) = {\bf{I}}\sigma _i^2 - \sigma _i^2{\mathbf{G}}_i^T{\bf{V}}^{ - 1}{\mathbf{G}}_i\sigma _i^2$ and (τ,ω) = (0,0).

Repeat E-step and M-step until convergence is satisfied.

Owing to o_i = 50, 100, and 150, so three models would be established by the above procedures. Their AIC values were calculated in order to pick up an optimal model.

Likelihood ratio test

Based on the estimate of marker effect β_i in the optimal model, all the markers with $\left| {\hat \beta _i} \right| \le 10^{ - 4}$ are deemed not to be associated with the trait. The other markers with the effects θ = {β₍₁₎,…,β_(O)} are potentially associated with the trait. To test the null hypothesis H₀:β_(i) = 0, which is no QTN linked to the ith marker, LR test was conducted by

$${\rm LR}_i = - 2\left[ {L\left( {\theta _{ - i}} \right) - L\left( \theta \right)} \right]$$

(14)

where $\theta _{ - i} = \left\{ {\beta _{(1)}, \cdots ,\beta _{(i - 1)},\beta _{(i + 1)}, \cdots ,\;\beta _{(O)}} \right\}^{\rm T}$, $L(\theta ) = \mathop {\sum}\nolimits_{i = 1}^n {\ln } \phi (y_i;{\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o} ,\sigma _e^2)$ is log-likelihood function, $\phi (y_i;{\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o} ,\sigma _e^2)$ is a normal density with mean ${\mathbf{1}}\mu + \mathop {\sum}\nolimits_{o = 1}^O {{\mathbf{G}}_o\beta _o}$ and variance $\sigma _e^2$, and LOD = LR/4.605. Although the general 0.05 critical value may be used for significance test, we decided to set up a slightly more stringent criterion of LOD = 3.0. The criterion is frequently adopted in linkage analysis and is the equivalent of $P = \Pr (\chi _1^2 > 3.0 \times 4.605) \approx 0.0002$, in which $\chi _1^2$ under H₀, follows a $\chi _{}^2$ distribution with one degree of freedom.

The flow diagram of pKWmEB is shown in Fig. 1. pKWmEB has been implemented in R and its software can be downloaded from https://cran.r-project.org/web/packages/mrMLM/index.html.

Fig. 1

A flow chart of pKWmEB method

Genome-wide efficient mixed model association

This is an existing GWAS method (Zhou and Stephens 2012) and used as a gold standard for comparison. This method is the fixed model version of the original MLM, in which β_i was treated as fixed effect with no distribution assigned. The method was implemented in the C software GEMMA (Zhou and Stephens 2012) (http://www.xzlab.org/software.html). The threshold of P-value was set as 0.05/p after Bonferroni correction for multiple tests, where p is the number of markers.

Monte Carlo simulation experiments

Five Monte Carlo simulation experiments were used to validate pKWmEB. In the first experiment, all the SNP genotypes were derived from 216,130 SNPs in Atwell et al. (2010) and 2000 SNPs were randomly sampled from each chromosome. The positions for the sampled SNPs were described by Wang et al. (2016). The sample size was the number of accessions (199) in Atwell et al. (2010). Six QTNs were simulated and placed on the SNPs with allelic frequencies of 0.30; their heritabilities were set as 0.10, 0.05, 0.05, 0.15, 0.05, and 0.05, respectively; and their positions and effects were listed on Table S1. Using $h_{\rm T}^2 = \sigma _G^2/\left( {\sigma _G^2 + \sigma _e^2} \right)$ = 0.05 × 4 + 0.10 + 0.15 = 0.45 and residual variance $\sigma _e^2 = 10.0$, total genetic variance for six simulated QTNs ($\sigma _G^2$) and individual genetic variance for each simulated QTN ($\sigma _r^2$,r = 1,…,6) could be obtained. $\sigma _r^2$ was a function of QTN effect and frequency of common allele. Thus, QTN effect could be obtained. The average was set at 10.0. The new phenotypes were simulated by the model: $y = \mu + \mathop {\sum}\limits_{i = 1}^6 {x_ib_i + \varepsilon }$, where ε~MVN_n(0,10 × I_n). The simulation was replicated 1000 times. In the Kruskal–Wallis test, the o_i most associated SNPs were selected and placed into multi-locus model. A detected QTN within 1 kb of the simulated QTN was considered to be a true QTN. For each simulated QTN, we counted the samples in which the LOD statistic exceeded 3.0. The ratio of the number of such samples to the total number of replicates (1000) represented the empirical power of this QTN. FPR was calculated as the ratio of the number of false positive effects to the total number of zero effects considered in the full model. To measure the variance and bias of gene effect estimate, mean squared error (MSE)

$${\rm MSE}_k = \frac{1}{{1000}}\mathop {\sum}\limits_{i = 1}^{1000} {\left( {\hat \beta _{k(i)} - \beta _k} \right)^2}$$

(15)

was calculated, where $\hat \beta _{k(i)}$ is the estimate of β_k in the ith sample.

To investigate the effect of polygenic background on pKWmEB, polygenic effects were simulated in the second experiment by multivariate normal distribution ${\mathrm{MVN}}_n(0,\sigma _{pg}^2{\mathbf{K}})$, where $\sigma _{{\rm pg}}^2$ is polygenic variance and K is kinship matrix between a pair of individuals. Here $\sigma _{{\rm pg}}^2 = 2$, so $h_{pg}^2 = 0.092$. The QTN size (h²), average, residual variance, and other parameter values were the same as those in the first experiment, and all the parameters were listed on Table S2. The new phenotypes were simulated by the model: $y = \mu + \mathop {\sum}\nolimits_{i = 1}^6 {x_ib_i + u + \varepsilon }$, where u~MVN_n(0,2 × K) and ε~MVN_n(0,10 × I_n).

To investigate the effect of epistatic background on pKWmEB, three epistatic QTNs were simulated in the third simulation experiment. The related parameters for the three epistatic QTNs were described in Wang et al. (2016). The QTN sizes (h²), average, residual variance, and other parameter values were also the same as those in the first experiment, and all the parameters were listed on Table S3. The new phenotypes were simulated by $y = \mu + \mathop {\sum}\nolimits_{i = 1}^6 {x_ib_i + \mathop {\sum}\nolimits_{j = 1}^3 {(A_j\# B_j)b_{jj}} + \varepsilon }$, where ε~MVN_n(0,10 × I_n), b_jj is the epistatic effect and A_j#B_j is its incidence coefficient.

All simulated data sets are available from https://doi.org/10.5061/dryad.sk652 (the Dryad Digital Repository).

To investigate the effect of skewed phenotypic distribution on pKWmEB, normal distribution for residual error in the first simulation experiment was replaced by log-normal distribution in the fourth simulation experiment and logistic distribution in the fifth simulation experiment, and other parameter values were the same as those in the first simulation experiment. To let residual error variance be 10, the standard deviation was set at 1.144 in log-normal distribution and 1.743 in logistic distribution. The means for the two skewed distributions were also zero. The two simulation data sets were included in Data set S2.

Results

Monte Carlo simulation studies

Statistical power for QTN detection

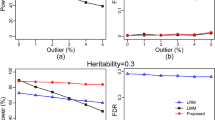
To validate pKWmEB, five simulation experiments were conducted. In the first simulation experiment, each sample was analyzed by five methods: pKWmEB, the new method without polygenic background control (KWmEB), Kruskal–Wallis test with Bonferroni correction (KWsBC), genome-wide EMMA (GEMMA), and multi-locus random-SNP-effect MLM (mrMLM). All the power results are shown in Table S1 and Fig. 2a. Clearly, the average powers for the above five methods were 69.8, 67.3, 60.7, 46.0, and 68.6 (%), respectively, indicating the highest average power of pKWmEB (Fig. 2a). More importantly, the power using pKWmEB was significantly higher than those using KWmEB and GEMMA (Table 1). Note that there were four QTNs with the same 5% heritability. The standard deviation of powers across the four QTNs might be used to measure the robustness of each method. As a result, the standard deviation was 13.01 for pKWmEB, 11.98 for KWmEB and 10.57 for mrMLM, which were much less than 35.17 for KWsBC, indicating the better stability of pKWmEB. On one occasion, the power for the fifth QTN using pKWmEB was 47.7% less than that using KWsBC. To further confirm the effectiveness of pKWmEB, polygenic effect simulated by multivariate normal distribution (r² = 9.2%) was added to each phenotypic observation in the second simulation experiment and the polygenic background was replaced by three epistatic QTN (r² = 15%) in the third simulation experiment. These results are listed in Tables S2 and S3, which show that the average powers for the above five methods were 69.1, 67.7, 58.9, 42.5, and 67.6 (%) in the second simulation experiment (Table S2; Fig. 2b), and 61.9, 59.9, 54.9, 39.1, and 58.9 (%), respectively, in the third simulation experiment (Table S3; Fig. 2c). The standard deviation of statistical powers among all the 5% QTNs was 21.31 for pKWmEB and 31.39 for KWsBC in the second simulation experiment, and 15.05 for pKWmEB and 40.77 for KWsBC in the third simulation experiment. Similarly, the power for the fifth QTN using pKWmEB was 47.2 and 68.3 (%) less than those using KWsBC in the second and third simulation experiments, respectively. In addition, residual error distributions in the above three experiments were replaced by log-normal (the fourth simulation experiment) and logistic (the fifth simulation experiment) distributions. The average powers for the above five methods were 76.2, 74.4, 80.1, 53.9, and 78.3 (%) in the fourth simulation experiment (Table S4; Fig. 2d), and 68.7, 66.9, 60.9, 44.1, and 68.0 (%), respectively, in the fifth simulation experiment (Table S5; Fig. 2e). Similar phenomena were observed for the fifth QTN and the standard deviation of statistical powers across all the 5% QTNs in the last two experiments. In summary, pKWmEB with polygenic background control is better than KWmEB without polygenic background control; pKWmEB retains the high power of KWsBC, and it is better in the stability of statistical power than KWsBC.

Fig. 2

Comparison of statistical powers of six simulated QTNs using five GWAS methods (pKWmEB, KWmEB, KWsBC, GEMMA, and mrMLM). a No polygenic background; b an additive polygenic variance (explaining 0.092 of the phenotypic variance); c three epistatic QTNs each explaining 0.05 of the phenotypic variance. Residual error is normal distribution with mean zero and variance 10 in (a) to (c), log-normal distribution with mean zero and standard deviation 1.144 (d), and logistic distribution with mean zero and standard deviation 1.743 (e)

Table 1 Paired t tests and their P-values for power and mean squared error (MSE) between pKWmEB and each of the other four methods in the first simulation experiment

Accuracies of estimated QTN effects

The accuracy of QTN effect estimation was measured by MSE and smaller MSE indicates higher accuracy of parameter estimation. All the MSE results from four approaches in the five simulation experiments are shown in Fig. 3 and Tables S6–S10, because KWsBC does not provide the estimates for QTN effects. Results showed that the average MSEs using pKWmEB, KWmEB, GEMMA, and mrMLM were 0.0797, 0.0825, 0.5467, and 0.0940 in the first simulation experiment, respectively, indicating the minimum average MSE of pKWmEB (Fig. 3a and Table S6). More importantly, the MSE using pKWmEB was almost significantly less than that using GEMMA (Table 1). Almost similar trends were found in the other simulation experiments (Tables S16–S19, Figs. 3a–e). Average value of each QTN effect across 1000 replicates was listed in Tables S11–S15. These results were also confirmed the above trends.

Fig. 3

Comparison of mean squared errors of each simulated QTN effect using four GWAS methods (pKWmEB, KWmEB, GEMMA, and mrMLM). The descriptions in (a) to (e) are the same as those in Fig. 2

False positive rate

The FPR is similar to the empirical Type 1 error rate. The FPRs in all the five simulation experiments were 0.0356 ± 0.0085 (%) for pKWmEB, 0.0385 ± 0.0073 (%) for KWmEB, 0.6130 ± 0.1644 (%) for KWsBC, 0.0290 ± 0.0094 (%) for GEMMA and 0.0214 ± 0.0043 (%) for mrMLM (Fig. 4 and Tables S1–S5). In summary, the FPRs are less than 0.05 % for pKWmEB, KWmEB, mrMLM, and GEMMA, and more than 0.60 % for KWsBC, indicating the best FPR control of pKWmEB even if a less stringent significant criterion was adopted.

Fig. 4

Comparison of false positive rates using five GWAS methods (pKWmEB, KWmEB, KWsBC, GEMMA, and mrMLM). The descriptions in (a) to (e) are the same as those in Fig. 2

Computational efficiency

Each sample in the first simulation experiment was analyzed by pKWmEB, KWmEB, KWsBC, mrMLM, and GEMMA. These analyses were implemented on the computer (Intel(R) Xeon(R) CPU E5-2637 v2 @ 3.50 GHz CPU). As a result, the computing times using the above five methods were 35.30, 35.20, 32.63, 13.08, and 1.63 (hours), respectively (Fig. S1). Although pKWmEB runs slightly longer than KWsBC, pKWmEB has significantly lower FPR than KWsBC.

Real data analysis in Arabidopsis thaliana

Four flowering time related traits in Arabidopsis thaliana derived from Atwell et al. (2010) were re-analyzed by pKWmEB, KWmEB, mrMLM, and GEMMA. The four flowering time related traits were FLC gene expression (FLC), FRI gene expression (FRI), days to flowering of plants grown in the field (FT Field) and days to flowering growth in greenhouse (FT GH). We also downloaded the results of EMMA from Atwell et al. (2010), with the significance criterion of Bonferroni correction (0.05/p, p is the number of markers). All the results are listed in Table S23. Results showed that the numbers of SNPs significantly associated with the four traits were 80 for pKWmEB, 77 for KWmEB, 56 for mrMLM, and 53 for GEMMA.

These significantly associated SNPs were used to mine candidate genes associated with the traits. These candidate genes were compared with those in previous studies. All the previously reported genes detected by the above four methods are listed in Table S24. As a result, 23, 16, 10, and 5 previously reported genes were found to be in the region of the significantly associated SNPs detected by pKWmEB, KWmEB, mrMLM, and GEMMA, respectively (Table S23), indicating that pKWmEB identified the most previously reported genes. Among these known genes, five were identified only by pKWmEB and were not included in the list of the previously reported genes in Atwell et al. (2010) (Table 2).

Table 2 Previously reported genes that were identified only by pKWmEB

Discussion

Recently, our group has developed several multi-locus GWAS methods, i.e., mrMLM (Wang et al. 2016), FASTmrEMMA (Wen et al. 2017), ISIS EM-BLASSO (Tamba et al. 2017), and pLARmEB (Zhang et al. 2017). Actually, these are parametric methods. As we know, nonparametric GWAS methods are also very useful in GWAS. However, polygenic background in the nonparametric methods isn’t controlled, so their FPRs are high. To overcome this issue, we developed pKWmEB in this study. In addition, pKWmEB can find some previously reported genes that aren’t detected by parametric methods (Table 2).

No existing nonparametric methods in GWAS have considered polygenic background control. This leads to the inflation of FPR. To overcome this issue, the model transformation of Wen et al. (2017) is used to whiten the covariance matrix of the polygenic matrix K and environmental noise. Meanwhile, genotypic incidence matrix and phenotypes are also transferred. Owing to continually transferred genotypic values, it is necessary to change the transferred genotypic values into binary variables (1 and −1) in order to carry out Kruskal–Wallis test. The question is how to conduct this transfer. If the values are larger than their mean or median, the values are transferred into 1. If the values are not larger than their mean or median, the values are transferred into −1. Thus, new incidence values are obtained. These new incidence values along with new phenotypes are used to conduct the Kruskal–Wallis test. Using this test, all the markers potentially associated with the trait are identified. These selected markers are placed into a multi-locus model, and original genotype and phenotype information is used to estimate their effects using empirical Bayes. Thus, true QTNs can be identified. Our results showed that mean threshold is better than median threshold in statistical power (Fig. S3 and Table S22). Although the Kruskal–Wallis test is used in this study, in addition, other nonparametric tests are also available, for example, the Jonckheere–Terpstra test (Terpstra 1952; Jonckheere 1954) and Anderson–Darling test (Anderson and Darling 1952 1954). As compared with the methods without polygenic background control, the new method demonstrates a significant improvement in statistical power and robustness for QTN detection and in accuracy for QTN-effect estimation.

In real data analysis, we should consider whether it is necessary to include population structure in the genetic model. Recently, Bulik-Sullivan et al. (2015) proposed a linkage disequilibrium score regression test to solve this issue. This method is to test the significance of difference between regression intercept and one. Results showed that population structure should be included in multi-locus model for all the four traits in this study (Table S25). Principal component analysis is also available for this purpose. We also need to consider the heterozygotes. In this case, a heterozygote is coded as zero and the others are the same as those in pKWmEB. If so, there is no significant power difference between the two homozygote genotypes (AA and aa) and the three genotypes (AA, Aa, and aa). However, the accuracy of QTN effect estimation significantly decreased as compared with no heterozygotes (Table S20 and S21).

The current nonparametric GWAS methods are almost a single-locus genome scan analysis, and such a single-marker test often requires a Bonferroni correction. To control the experimental error at a genome-wide significance level of 0.01, the significance level for each test should be adjusted as 0.01/p, which is 1e−8 if there are one million markers (p). This criterion is too stringent to detect many important loci. To avoid this issue, many multi-locus approaches have been suggested (Segura et al. 2012; Moser et al. 2015; Wang et al. 2016). In these multi-locus approaches, there is no need for such a multiple test correction. At this situation, less stringent critical P-value (~2e−4, which is the equivalent of LOD = 3.0) can be adopted. This is because its FPR is similar to that from single-locus genome scan analysis with a stringent significance criterion.

In Monte Carlo simulation studies, the estimates of powers for the four QTNs with the same effect size are highly variable. This is different from the situation in quantitative trait locus mapping. To dissect this phenomenon, the simulated data sets in this study were also analyzed by ADGWAS of Yang et al. (2014) and Jonckheere–Terpstra test with Bonferroni correction (Liu 2016). As a result, similar phenomenon was observed as well. This may be due to two reasons. One is about the genotypic data sets, which are derived from the 216130 SNPs in Atwell et al. (2010). Several significant correlations of genotypes between a pair of QTNs were observed. This is not similar to ideal segregation populations in linkage analysis. Another is about single-locus genome-wide scanning of nonparametric tests. When KWsBC is implemented in the first simulation experiment, the 85.6, 46.9, 14.2, and 70.9 (%) P-values in the detection of the second, third, fifth, and sixth QTNs are between 5e−6 and 0.01. Owing to the stringent Bonferroni correction criterion, QTN2 and QTN6 were not detected in most situations.

We compared the results in this study with those in Atwell et al. (2010), and found that individual previously reported genes are common, for example, FLA, AT4G00690 (similar to ESD4, 268809/276143 bp on chromosome 4) and ATARP4 (6371569 bp on chromosome 1) are detected by all the four methods. However, most previously reported genes depend on methods (Table S24) and some previously reported genes are detected only by pKWmEB (Table 2). This indicates that pKWmEB is a complement to the widely used GWAS methods (such as GEMMA). The possible reason is that each method has its own distinct assumptions.

Data archiving

All simulated data sets are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.sk652 and supplementary file (Simulated phenotypes Data Sets). The real data set can be retrieved from: http://www.arabidopsis.org/.