Abstract
Quantum physics can be exploited to generate true random numbers, which have important roles in many applications, especially in cryptography. Genuine randomness from the measurement of a quantum system reveals the inherent nature of quantumness—coherence, an important feature that differentiates quantum mechanics from classical physics. The generation of genuine randomness is generally considered impossible with only classical means. On the basis of the degree of trustworthiness on devices, quantum random number generators (QRNGs) can be grouped into three categories. The first category, practical QRNG, is built on fully trusted and calibrated devices and typically can generate randomness at a high speed by properly modelling the devices. The second category is self-testing QRNG, in which verifiable randomness can be generated without trusting the actual implementation. The third category, semi-self-testing QRNG, is an intermediate category that provides a tradeoff between the trustworthiness on the device and the random number generation speed.
Similar content being viewed by others
Introduction
Random numbers have essential roles in many fields, such as cryptography,1 scientific simulations,2 lotteries and fundamental physics tests.3 These tasks rely on the unpredictability of random numbers, which generally cannot be guaranteed in classical processes. In computer science, random number generators (RNGs) are based on pseudo-random number generation algorithms,4 which deterministically expand a random seed. Although the output sequences are usually perfectly balanced between 0 and 1 s, a strong long-range correlation exists, which can undermine cryptographic security, cause unexpected errors in scientific simulations or open loopholes in fundamental physics tests.5–7
Many researchers have attempted to certify randomness solely based on the observed random sequences. In the 1950s, Kolmogorov developed the Kolmogorov complexity concept to quantify the randomness in a certain string.8 An RNG output sequence appears random if it has a high Kolmogorov complexity. Later, many other statistical tests9–11 were developed to examine randomness in the RNG outputs. However, testing an RNG from its outputs can never prevent a malicious RNG from outputting a predetermined string that passes all of these statistical tests. Therefore, true randomness can only be obtained via processes involving inherent randomness.
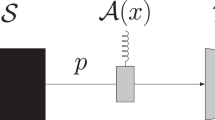
In quantum mechanics, a system can be prepared in a superposition of the (measurement) basis states, as shown in Figure 1. According to Born’s rule, the measurement outcome of a quantum state can be intrinsically random—i.e., it can never be predicted better than blindly guessing. Therefore, the nature of inherent randomness in quantum measurements can be exploited for generating true random numbers. Within a resource framework, coherence12 can be measured similarly to entanglement.13 By breaking the coherence or superposition of the measurement basis, it is shown that the obtained intrinsic randomness comes from the consumption of coherence. In turn, quantum coherence can be quantified from intrinsic randomness.14
Electron spin detection in the Stern–Gerlach experiment. Assume that the spin takes two directions along the vertical axis, denoted by |↑〉 and |↓〉. If the electron is initially in a superposition of the two spin directions, , detecting the location of the electron would break the coherence, and the outcome (↑ or ↓) is intrinsically random.
A practical QRNG can be developed using the simple process as shown in Figure 1. On the basis of the different implementations, there exists a variety of practical QRNGs. Generally, these QRNGs are featured for their high generation speed and a relatively low cost. In reality, quantum effects are always mixed with classical noises, which can be subtracted from the quantum randomness after properly modelling the underlying quantum process.15
The randomness in the practical QRNGs usually suffices for real applications if the model fits the implementation adequately. However, such QRNGs can generate randomness with information-theoretical security only when the model assumptions are fulfilled. In the case that the devices are manipulated by adversaries, the output may not be genuinely random. For example, when a QRNG is wholly supplied by a malicious manufacturer, who copies a very long random string to a large hard drive and only outputs the numbers from the hard drive in sequence, the manufacturer can always predict the output of the QRNG device.
On the other hand, a QRNG can be designed in such a way that its output randomness does not rely on any physical implementations. True randomness can be generated in a self-testing way even without perfectly characterising the realisation instruments. The essence of a self-testing QRNG is based on device-independently witnessing quantum entanglement or non-locality by observing a violation of the Bell inequality.3 Even if the output randomness is mixed with uncharacterised classical noise, we can still get a lower bound on the amount of genuine randomness based on the amount of non-locality observed. The advantage of this type of QRNG is the self-testing property of the randomness. However, because the self-testing QRNG must demonstrate non-locality, its generation speed is usually very low. As the Bell tests require random inputs, it is crucial to start with a short random seed. Therefore, such a randomness generation process is also called randomness expansion.
In general, a QRNG comprises a source of randomness and a readout system. In realistic implementations, some parts may be well characterised, while others are not. This motivates the development of an intermediate type of QRNG, between practical and fully self-testing QRNGs, which is called semi-self-testing. Under several reasonable assumptions, randomness can be generated without fully characterising the devices. For instance, faithful randomness can be generated with a trusted readout system and an arbitrary untrusted randomness resource. A semi-self-testing QRNG provides a trade off between practical QRNGs (high performance and low cost) and self-testing QRNGs (high security of certified randomness).
In the past two decades, there has been tremendous development for all the three types of QRNG: trusted device, self-testing and semi-self-testing. In fact, there are commercial QRNG products available in the market. A brief summary of representative practical QRNG demonstrations that highlights the broad variety of optical QRNG is presented in Table 1. These QRNG schemes will be discussed further in Sections ‘Trusted-device QRNG I: single-photon detector’ and ‘Trusted-device QRNG II: macroscopic photodetector’. A summary of self-testing and semi-self-testing QRNG demonstrations is presented in Table 2, which will be reviewed in detail in Sections ‘Self-testing QRNG’ and ‘Semi-self-testing QRNGs’.
Trusted-device QRNG I: single-photon detector
True randomness can be generated from any quantum process that breaks coherent superposition of states. Because of the availability of high-quality optical components and the potential of chip-size integration, most of today’s practical QRNGs are implemented in photonic systems. In this survey, we focus on various implementations of optical QRNGs.
A typical QRNG includes an entropy source for generating well-defined quantum states and a corresponding detection system. The inherent quantum randomness in the output is generally mixed with classical noises. Ideally, the extractable quantum randomness should be well quantified and be the dominant source of the randomness. By applying randomness extraction, genuine randomness can be extracted from the mixture of quantum and classical noise. The extraction procedure is detailed in Materials and Methods.
Qubit state
Random bits can be generated naturally by measuring a qubit. (A qubit is a two-level quantum-mechanical system, which, similar to a bit in classical information theory, is the fundamental unit of quantum information.) in the Z basis, where |0〉 and |1〉 are the eigenstates of the measurement Z. For example, Figure 2a shows a polarisation-based QRNG, where |0〉 and |1〉 denote horizontal and vertical polarisation, respectively, and |+〉 denotes +45° polarisation. Figure 2b presents a path-based QRNG, where |0〉 and |1〉 denote the photon travelling via path R and T, respectively.
Practical QRNGs based on single-photon measurement. (a) A photon is originally prepared in a superposition of horizontal (H) and vertical (V) polarisations, described by . A polarising beam splitter (PBS) transmits the horizontal and reflects the vertical polarisation. For random bit generation, the photon is measured by two single-photon detectors (SPDs). (b) After passing through a symmetric beam splitter (BS), a photon exists in a superposition of transmitted (T) and reflected (R) paths, . A random bit can be generated by measuring the path information of the photon. (c) QRNG based on measurement of photon arrival time. Random bits can be generated, for example, by measuring the time interval, ∆t, between two detection events. (d) QRNG based on measurements of photon spatial mode. The generated random number depends on spatial position of the detected photon, which can be read out by an SPD array.
The most appealing property of this type of QRNGs lies on their simplicity in theory that the generated randomness has a clear quantum origin. This scheme was widely adopted in the early development of QRNGs.16–18 As at most one random bit can be generated from each detected photon, the random number generation rate is limited by the detector’s performance, such as dead time and efficiency. For example, the dead time of a typical silicon SPD based on an avalanche diode is tens of nanoseconds.19 Therefore, the random number generation rate is limited to tens of Mbps, which is too low for certain applications such as high-speed quantum key distribution (QKD), which can be operated at GHz clock rates.20,21 Various schemes have been developed to improve the performance of QRNG based on SPD.
Temporal mode
One way to increase the random number generation rate is to perform measurement on a high-dimensional quantum space, such as measuring the temporal or spatial mode of a photon. Temporal QRNGs measure the arrival time of a photon, as shown in Figure 2c. In this example, the output of a continuous-wave laser is detected by a time-resolving SPD. The laser intensity can be carefully controlled such that within a chosen time period T there is roughly one detection event. The detection time is randomly distributed within the time period T and digitised with a time resolution of δt. The time of each detection event is recorded as raw data. Thus, for each detection, the QRNG generates about log2(T /δt) bits of raw random numbers. Essentially, δt is limited by the time jitter of the detector (typically in the order of 100 ps), which is normally much smaller than the detector deadtime (typically in the order of 100 ns).19
One important advantage of temporal QRNGs is that more than one bit of random number can be extracted from a single-photon detection, thus improving the random number generation rate. The time period T is normally set to be comparable to the detector deadtime. Comparing with the qubit QRNG, the temporal-mode QRNG alleviates the impact of detection deadtime. For example, if the time resolution and the dead time of an SPD are 100 ps and 100 ns, respectively, the generation rate of temporal QRNG is around log2(1,000)×10 Mbps, which is higher than that of the qubit scheme (limited to 10 Mbps). The temporal QRNGs have been well studied recently.22–26
Spatial mode
Similar to the case of temporal QRNG, multiple random bits can be generated by measuring the spatial mode of a photon with a space-resolving detection system. One illustrative example is to send a photon through a 1×N beam splitter and to detect the position of the output photon. Spatial QRNG has been experimentally demonstrated by using a multi-pixel single-photon detector array,27 as shown in Figure 2d. The distribution of the random numbers depends on both the spatial distribution of light intensity and the efficiency uniformity of the SPD arrays.
The spatial QRNG offers similar properties as the temporal QRNG, but it requires multiple detectors. In addition, correlation may be introduced between the random bits because of cross talk between different pixels in the closely packed detector array.
Multiple photon-number states
Randomness can be generated not only from measuring a single photon but also from quantum states containing multiple photons. For instance, a coherent state
is a superposition of different photon-number (Fock) states {|n〉}, where n is the photon number and |α|2 is the mean photon number of the coherent state. Thus, by measuring the photon number of a coherent laser pulse with a photon number-resolving SPD, we can obtain random numbers that follow a Poisson distribution. QRNGs based on measuring photon number have been successfully demonstrated in experiments.28–30 Interestingly, random numbers can be generated by resolving photon-number distribution of a light-emitting diode (LED) with a consumer-grade camera inside a mobile phone, as shown in a recent study.31
Note that the above scheme is sensitive to both the photon-number distribution of the source and the detection efficiency of the detector. In the case of a coherent state source, if the loss can be modelled as a beam splitter, the low detection efficiency of the detector can be easily compensated by using a relatively strong laser pulse.
Trusted-device QRNG II: macroscopic photodetector
The performance of an optical QRNG largely depends on the detection device used. Besides SPD, high-performance macroscopic photodetectors have also been applied in various QRNG schemes. This is similar to the case of QKD, where protocols based on optical homodyne detection32 have been developed, with the hope to achieve a higher key rate over a low-loss channel. In the following discussion, we review two examples of QRNG implemented with macroscopic photodetector.
Vacuum noise
In quantum optics, the amplitude and phase quadratures of the vacuum state are represented by a pair of non-commuting operators (X and P with [X, P]=i/2), which cannot be determined simultaneously with an arbitrarily high precision33—i.e., 〈(∆X)2〉×〈(∆P)2〉⩾1/16, with ∆O defined by O −〈O〉 and 〈O〉 denoting the average of O. This can be easily visualised in the phase space, where the vacuum state is represented by a two-dimensional Gaussian distribution centred at the origin with an uncertainty of 1/4 (the shot-noise variance) along any directions, as shown in Figure 3a. In principle, Gaussian distributed random numbers can be generated by measuring any field quadrature repeatedly. This scheme has been implemented by sending a strong laser pulse through a symmetric beam splitter and detecting the differential signal of the two output beams with a balanced receiver.34–36
QRNGs using macroscopic photodetector. (a) Phase-space representation of the vacuum state. The variance of the X-quadrature is 1/4. (b) QRNG based on vacuum noise measurements. The system comprises a strong local oscillator (LO), a symmetric beam splitter (BS), a pair of photon detectors (PD) and an electrical subtracter (Sub). (c) Phase-space representation of a partially phase-randomised coherent state. The variance of the X-quadrature is in the order of n×〈∆θ2〉, where n is the average photon number and 〈∆θ2〉 is the phase noise variance. (d) QRNGs based on measurements of laser phase noise. The first coupler splits the original laser beam into two beams, which propagate through two optical fibres of different lengths, thereafter interfering at the second coupler. The output signal is recorded by a photon detector. The extra length ∆L in one fibre introduces a time delay Td between the two paths, which in turn determines the variance of the output signal.
Given that the local oscillator is a single-mode coherent state and the detector is shot-noise limited, the random numbers generated in this scheme follow a Gaussian distribution, which is on demand in certain applications, such as Gaussian-Modulated Coherent States (GMCS) QKD.32 There are several distinct advantages of this approach. First, the resource of quantum randomness, the vacuum state, can be easily prepared with a high fidelity. Second, the performance of the QRNG is insensitive to detector loss, which can be simply compensated by increasing the local oscillator power. Third, the field quadrature of vacuum is a continuous variable, suggesting that more than one random bit can be generated from one measurement. For example, 3.25 bits of random numbers are generated from each measurement.34
In practice, an optical homodyne detector itself contributes additional technical noise, which may be observed or even controlled by a potential adversary. A randomness extractor is commonly required to generate secure random numbers. To extract quantum randomness effectively, the detector should be operated in the shot noise-limited region, in which the overall observed noise is dominated by vacuum noise. We remark that building a broadband shot noise-limited homodyne detector operating above a few hundred MHz is technically challenging.37–39 This may in turn limit the ultimate operating speed of this type of QRNG.
Amplified spontaneous emission
To overcome the bandwidth limitation of shot noise-limited homodyne detection, researchers have developed QRNGs based on measuring phase40–45 or intensity noise46,47 of amplified spontaneous emission(ASE), which is quantum mechanical by nature.15,48,49
In the phase noise-based QRNG scheme, random numbers are generated by measuring a field quadrature of phase-randomised weak coherent states (signal states). Figure 3c shows the phase-space representation of a signal state with an average photon number of n and a phase variance of 〈(∆θ)2〉. If the average phase of the signal state is around π/2, the uncertainty of the X-quadrature is of the order of n〈(∆θ)2〉. When n is large, this uncertainty can be significantly larger than the vacuum noise. Therefore, phase noise-based QRNG is more robust against detector noise. In fact, this scheme can be implemented with commercial photo-detectors operated above GHz rates.
QRNG based on laser phase noise was first developed using a cw laser source and a delayed self-heterodyning detection system,40 as shown in Figure 3d. Random numbers are generated by measuring the phase difference of a single-mode laser at times t and t+Td. Intuitively, if the time delay Td is much larger than the coherence time of the laser, the two laser beams interfering at the second beam splitter can be treated as generated by independent laser sources. In this case, the phase difference is a random variable uniformly distributed in [−π, π), regardless of the classical phase noise introduced by the unbalanced interferometer itself. This suggests that a robust QRNG can be implemented without phase-stabilising the interferometer. On the other hand, by phase-stabilising the interferometer, the time delay Td can be made much shorter than the coherent time of the laser,40 enabling a much higher sampling rate. This phase-stabilisation scheme has been adopted in a ≥6 Gbps QRNG42 and a 68-Gbps QRNG demonstration.45
Phase noise-based QRNG has also been implemented using a pulsed laser source, in which the phase difference between adjacent pulses is automatically randomised.41,43,44 A speed of 80 Gbps (raw rate as shown in Table 1) has been demonstrated.43 It also played a crucial role in a recent loophole-free Bell experiment.50 Here we want to emphasise that, strictly speaking, none of these generation speeds are real time, because of the speed limitation of the randomness extraction.15 Although such a limitation is rather technical, in practice, it is important to develop extraction schemes and hardware that can match the fast random bit generation speed in the future.
Self-testing QRNG
Realistic devices inevitably introduce classical noise that affects the output randomness, thus causing the generated random numbers depending on certain classical variables, which might open up security issues. To remove this bias, one must properly model the devices and quantify their contributions. In the QRNG schemes described in Sections ‘Trusted-device QRNG I: single-photon detector’ and ‘Trusted-device QRNG II: macroscopic photodetector’, the output randomness relies on the device models.15,49 When the implementation devices deviate from the theoretical models, the randomness can be compromised. In this section, we discuss self-testing QRNGs, whose output randomness is certified independent of device implementations.
Self-testing randomness expansion
In QKD, secure keys can be generated even when the experimental devices are not fully trusted or characterised.51,52 Such self-testing processing of quantum information also occurs in randomness generation (expansion). The output randomness can be certified by observing violations of the Bell inequalities;3 see Figure 4. Under the no-signalling condition53 in the Bell tests, it is impossible to violate Bell inequalities if the output is not random or predetermined by local hidden variables.
Illustration of a bipartite Bell test. For random inputs x and y, two spacelikely separated parties Alice and Bob output a and b, respectively, without any signaling. A Bell inequality is defined as a linear combination of the probabilities p(a,b|x,y). For instance, the Clauser–Horne–Shimony–Holt (CHSH) inequality56 is defined by , where all of the inputs and outputs are bit values, and SC is the classical bound for all local hidden-variable models. With quantum settings, that is, performing measurements on quantum state ρAB, , the CHSH inequality can be violated up to . Quantum features (such as intrinsic randomness) manifest as violations of the CHSH inequality.
As Colbeck54,55 suggested that randomness can be expanded by untrusted devices, several protocols based on different assumptions have been proposed. For instance, in a non-malicious device scenario, we can consider that the devices are honestly designed but get easily corrupt by unexpected classical noises. In this case, instead of a powerful adversary that may entangle with the experiment devices, we can consider a classical adversary who possesses only classical knowledge of the quantum system and analyses the average randomness output conditioned by the classical information. On the basis of the Clauser–Horne–Shimony–Holt (CHSH) inequality,56 Fehr et al.57 and Pironio et al.58 proposed self-testing randomness expansion protocols against classical adversaries. The protocols quadratically expand the input seed, implying that the length of the input seed is , where n denotes the experimental iteration number.
A more sophisticated exponential randomness expansion protocol based on the CHSH inequality was proposed by Vidick and Vazirani,59 in which the lengths of the input seed is O(log2 n). In the same work, they also presented an exponential expansion protocol against quantum adversaries, where quantum memories in the devices may entangle with the adversary. The Vidick–Vazirani protocol against quantum adversaries places strict requirements on the experimental realisation. Miller and Shi60 partially solved this problem by introducing a more robust protocol. Combined with the work by Chung et al.,61 they also presented an unbounded randomness expansion scheme. By adopting a more general security proof, Miller and Shi62 recently showed that genuinely randomness can be obtained as long as the CHSH inequality is violated. Their protocol greatly improves the noise tolerance, indicating that an experimental realisation of a fully self-testing randomness expansion protocol is feasible.
The self-testing randomness expansion protocol relies on a faithful realisation of Bell test excluding the experimental loopholes, such as locality and efficiency loopholes. The randomness expansion protocol against classical adversaries is first experimentally demonstrated by Pironio et al.63 in an ion-trap system, which closes the efficiency loophole but not the locality loophole.
To experimentally close the locality loophole, a photonic system is more preferable when quantum memories are unavailable. As the CHSH inequality is minimally violated in an optically realised system,64,65 the randomness output is also very small (with min-entropy of Hmin=7.2×10−5 in each run), and the randomness generation rate is 0.4 bits per s. To maximise the output randomness, the implementation settings are designed to maximally violate the CHSH inequality. Because of experimental imperfections, the chosen Bell inequality might be sub-optimal for the observed data. In this case, the output randomness can be optimised over all possible Bell inequalities.66,67
Although non-locality or entanglement certifies the randomness, the three quantities, non-locality, entanglement and randomness, are not equivalent.68 Maximum randomness generation does not require maximum non-local correlation or a maximum entangled state. In the protocols based on the CHSH inequality, maximal violation (non-locality and entanglement) generates 1.23 bits of randomness. It is shown that 2 bits of randomness can be certified with little involvement of non-locality and entanglement.68 Furthermore, as discussed in a more generic scenario involving non-locality and randomness, it is shown that maximally non-local theories cannot be maximally random.69
Randomness amplification
In self-testing QRNG protocols based on the assumption of perfectly random inputs, the output randomness is guaranteed by the violations of Bell tests. Conversely, when all the inputs are predetermined, any Bell inequality can be violated to an arbitrary feasible value without invoking a quantum resource. Under these conditions, all self-testing QRNG protocols cease to work any more. Nevertheless, randomness generation in the presence of partial randomness is still an interesting problem. Here an adversary can use the additional knowledge of the inputs to fake violations of Bell inequalities. The task of generating arbitrarily free randomness from partially free randomness is also called randomness amplification, which is impossible to achieve in classical processes.
The first randomness amplification protocol was proposed by Colbeck and Renner.70 Using a two-party chained Bell inequality,71,72 they showed that any Santha–Vazirani weak sources73 (defined in Methods), with ϵ<0.058, can be amplified into arbitrarily free random bits in a self-testing way by requiring only no-signalling. A basic question of randomness amplification is whether free random bits can be obtained from arbitrary weak randomness. This question was answered by Gallego et al.,74 who demonstrated that perfectly random bits can be generated using a five-party Mermin inequality75 with arbitrarily imperfect random bits under the no-signalling assumption.
Randomness amplification is related to the freewill assumption5–7,76–79 in Bell tests. In experiments, the freewill assumption requires the inputs to be random enough such that violations of Bell inequalities are induced from quantum effects rather than predetermined classical processes. This is extremely meaningful in fundamental Bell tests, which aim to rule out local realism. Such fundamental tests are the foundations of self-testing tasks, such as device-independent QKD and self-testing QRNG. Interestingly, self-testing tasks require a faithful violation of a Bell inequality, in which intrinsic random numbers are needed. However, to generate faithful random numbers, we in turn need to witness non-locality, which requires additional true randomness. Therefore, the realisations of genuine loophole-free Bell tests and, hence, fully self-testing tasks are impossible. Self-testing protocols with securities independent of the untrusted part can be designed only by placing reasonable assumptions on the trusted part.
Semi-self-testing QRNGs
Traditional QRNGs based on specific models pose security risks in fast random number generation. On the other hand, the randomness generated by self-testing QRNGs is information-theoretically secure even without characterising the devices, but the processes are impractically slow. As a compromise, intermediate QRNGs might offer a good tradeoff between trusted and self-testing schemes—realising both reasonably fast and secure random number generation.
As shown in Figure 5, a typical QRNG comprises two main modules: a source that emits quantum states and a measurement device that detects the states and outputs random bits. In trusted-device QRNGs, both source and measurement devices15,49 must be modelled properly, whereas the output randomness in the fully self-testing QRNGs does not depend on the implementation devices.
In practice, there exist scenarios that the source (respectively, measurement device) is well characterised, whereas the measurement device (respectively, source) is not. Here we review the semi-self-testing QRNGs, where parts of the devices are trusted.
Source-independent QRNG
In source-independent QRNG, the randomness source is assumed to be untrusted, whereas the measurement devices are trusted. The essential idea for this type of scheme is to use the measurement to monitor the source in real time. In this case, normally one needs to randomly switch among different (typically, complement) measurement settings, so that the source (assumed to be under control of an adversary) cannot predict the measurement ahead. Thus, a short seed is required for the measurement choices.
In the illustration of semi-self-testing QRNG, Figure 5, the source-independent scheme is represented by a unique x (corresponding to a state ρx) and multiple choices of the measurement settings y. In Section ‘Trusted-device QRNG I: single-photon detector’, we present that randomness can be obtained by measuring |+〉 in the Z basis. However, in a source-independent scenario, we cannot assume that the source emits the state |+〉. In fact, we cannot even assume the dimension of the state ρx. This is the major challenge facing this type of scheme.
To faithfully quantify the randomness in the Z basis measurement, first a squashing model is applied so that the to-be-measured state is equivalent to a qubit.80 Note that this squashing model puts a strong restriction on measurement devices. Then, the measurement device should occasionally project the input state onto the X basis states, |+〉 and |−〉, and check whether the input is |+〉.81 The technique used in the protocol shares strong similarity with the one used in QKD.82 The X basis measurement can be understood as the phase error estimation, from which we can estimate the amount of classical noise. Similar to privacy amplification, randomness extraction is performed to subtract the classical noise and output true random values.
The source-independent QRNG is advantageous when the source is complicated, such as in the aforementioned QRNG schemes based on measuring single-photon sources,16–18 LED lights31 and phase fluctuation of lasers.42 In these cases, the sources are quantified by complicated or hypothetical physical models. Without a well-characterised source, randomness can still be generated. The disadvantage of this kind of QRNGs compared with fully self-testing QRNGs is that they need a good characterisation of the measurement devices. For example, the upper and the lower bounds on the detector efficiencies need to be known to avoid potential attacks induced from detector efficiency mismatch. In addition, the intensity of light inputs into the measurement device needs to be carefully controlled to avoid attacks on the detectors.
Recently, a continuous-variable version of the source-independent QRNG is experimentally demonstrated83 and achieves a randomness generation rate over 1 Gbps. Moreover, with state-of-the-art devices, it can potentially reach the speed in the order of tens of Gbps, which is similar to the trusted-device QRNGs. Hence, semi-self-testing QRNG is approaching practical regime.
Measurement-device-independent QRNGs
Alternatively, we can consider the scenario that the input source is well characterised, whereas the measurement device is untrusted. In Figure 5, different inputs ρx (hence multiple x) are needed to calibrate the measurement device with a unique setting y. Similar to the source-independent scenario, the randomness is originated by measuring the input state |+〉 in the Z basis. The difference is that here the trusted source sends occasionally auxiliary quantum states ρx, such as |0〉, to check whether the measurement is in the Z basis.84 The analysis combines measurement tomography with randomness quantification of positive-operator valued measure, and it does not assume to know the dimension of the measurement device—i.e., the auxiliary ancilla may have an arbitrary dimension.
The advantage of such QRNGs is that they remove all detector side channels, but the disadvantage is that they may be subject to imperfections in the modelling of the source. This kind of QRNG is complementary to the source-independent QRNG, and one should choose the proper QRNG protocol based on the experimental devices.
We now turn to two variations of measurement-device-independent QRNGs. First, the measurement tomography step may be replaced by a certain witness, which could simplify the scheme at the expense of a slightly worse performance. Second, similar to the source-independent case, a continuous-variable version of measurement device-independent QRNG might significantly increase the bit rate. The challenge lies on continuous-variable entanglement witness and measurement tomography.
Other semi-self-testing QRNGs
Apart from the above two types of QRNGs, there are also some other QRNGs that achieve self-testing except under some mild assumptions. For example, the source and measurement devices can be assumed to occupy independent two-dimensional quantum subspaces.85 In this scenario, the QRNG should use both different input states and different measurement settings. The randomness can be estimated by adopting a dimension witness.86 A positive value of this dimension witness could certify randomness in this scenario, similar to the fact that a violation of the Bell inequality could certify randomness of self-testing QRNG in Section ‘Self-testing QRNG’.
Outlook
The needs of ‘perfect’ random numbers in quantum communication and fundamental physics experiments have stimulated the development of various QRNG schemes, from highly efficient systems based on trusted devices to the more theoretically interesting self-testing protocols. On the practical side, the ultimate goal is to achieve fast random number generation at low cost, while maintaining a high level of randomness. With the recent development on wave-guide fabrication technique,87 we expect that chip-size, high-performance QRNGs could be available in the near future. To guarantee the output randomness, the underlying physical models for these QRNGs need to be accurate, and both the quantum noise and classical noise should be well quantified. Meanwhile, by developing a semi-self-testing protocol, a QRNG becomes more robust against classical noises and device imperfections. In the future, it is interesting to investigate the potential technologies that are required to make the self-testing QRNG practical. With the new development on single-photon detection, the readout part of the self-testing QRNG can be ready for practical application in the near future. The entanglement source, on the other hand, is still away from the practical regime (Gbps).
On the theoretical side, the study of self-testing QRNG has not only provided a means of generating robust randomness, but also greatly enriched our understanding on the fundamental questions in physics. In fact, even in the most recent loophole-free Bell experiment88–91 in which high-speed QRNG has played a crucial role, it is still arguable whether it is appropriate to use randomness generated based on quantum theory to test quantum physics itself. Other random resources have also been proposed for loophole-free Bell’s inequality tests, such as independent comic photons.92 It is an open question whether we can go beyond QRNG and generate randomness from a more general theory.
Materials and Methods
Min-entropy source
Given the underlying probability distribution, the randomness of a random sequence X on {0, 1}n can be quantified by its min-entropy
Santha–Vazirani weak sources
We assume that random bit numbers are produced in the time sequence x1, x2, ..., xj, .... Then, for 0<ϵ⩽1/2, the Santha–Vazirani weak source73 is called ϵ-free if
for all values of j. Here e represents all classical variables generated outside the future light-cone of the Santha–Vazirani weak sources.
Randomness extractor
An RNG typically consists of two components: an entropy source and a randomness extractor.87 In a QRNG, the entropy source could be a physical device whose output is fundamentally unpredictable, whereas the randomness extractor could be an algorithm that generates nearly perfect random numbers from the output of the above preceding entropy source, which can be imperfectly random. The two components of QRNG are connected by quantifying the randomness with min-entropy. The min-entropy of the entropy source is first estimated and then fed into the randomness extractor as an input parameter.
The imperfect randomness of the entropy source can already be seen in the SPD-based schemes, such as the photon-number detection scheme. By denoting N as the discrimination upper bound of a photon number-resolving detector, at most log2(N ) raw random bits can be generated per detection event. However, as the photon numbers of a coherent state source follows a Poisson distribution, the raw random bits follow a non-uniform distribution; consequently, we cannot obtain log2(N) bits of random numbers. To extract perfectly random numbers, we require a post-processing procedure (i.e., randomness extractor).
In the coherent detection-based QRNG, the quantum randomness is inevitably mixed with classical noises introduced by the detector and other system imperfections. Moreover, any measurement system has a finite bandwidth, implying unavoidable correlations between adjacent samples. Once quantified, these unwanted side effects can be eliminated through an appropriate randomness extractor.15
The composable extractor was first introduced in classical cryptography,93,94 and it was later extended to quantum cryptography.95,96 To generate information-theoretically provable random numbers, two typical extractors, the Trevisan’s extractor or the Toeplitz-hashing extractor, are generally used in practice.
Trevisan’s extractor97,98 has been proven to be secure against quantum adversaries.99 Moreover, it is a strong extractor (its seed can be reused) and its seed length is the polylogarithmic function of the input. Tevisan’s extractor comprises two main parts, a one-bit extractor and a combinatorial design. The Toeplitz-hashing extractor was well developed in the privacy amplification procedure of the QKD system.100 This kind of extractor is also a strong extractor.101 By applying the fast Fourier transformation technique, the runtime of the Toeplitz-hashing extractor can be improved to O(n log n).
On account of their strong extractor property, both of these extractors generate random numbers even when the random seed is longer than the output length of each run. Both extractors have been implemented15 and the speed of both extractors have been increased in follow-up studies,102,103 but they remain far below the operating speed of the QRNG based on laser-phase fluctuation (68 Gbps45). Therefore, the speed of the extractor is the main limitation of a practical QRNG.
References
Shannon, C . Communication theory of secrecy systems. Bell System Technical Journal 28, 656–715 (1949).
Metropolis, N . & Ulam, S . The monte carlo method. J. Am. Stat. Assoc. 44, 335–341 (1949).
Bell, J. On the einstein-podolsky-rosen paradox. Physics 1, 195–200 (1964).
Knuth, D. E. Art of Computer Programming, Volume 2: Seminumerical Algorithms. (Addison-Wesley Professional, 2014).
Kofler, J., Paterek, T. & Brukner, I. C. V. Experimenters freedom in bells theorem and quantum cryptography. Phys. Rev. A 73, 022104 (2006).
Hall, M. J. W. Local deterministic model of singlet state correlations based on relaxing measurement independence. Phys. Rev. Lett. 105, 250404 (2010).
Yuan, X., Cao, Z. & Ma, X. Randomness requirement on the clauser-horne-shimony-holt bell test in the multiple-run scenario. Phys. Rev. A 91, 032111 (2015).
Kolmogorov, A. On tables of random numbers. Theor. Comput. Sci. 207, 387–395 (1998).
Marsaglia, G. DIEHARD: a battery of tests of randomness. http://stat.fsu.edu/pub/diehard/ (1996).
Bassham III, L. E. et al. SP 800-22 Rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. (National Institute of Standards & Technology, Gaithersburg, MD, USA, 2010).
Kim, S.-J., Umeno, K. & Hasegawa, A. Corrections of the nist statistical test suite for randomness. arXiv:nlin/0401040.
Baumgratz, T., Cramer, M. & Plenio, M. B. Quantifying coherence. Phys. Rev. Lett. 113, 140401 (2014).
Bennett, C. H., Bernstein, H. J., Popescu, S. & Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 53, 2046–2052 (1996).
Yuan, X., Zhou, H., Cao, Z. & Ma, X. Intrinsic randomness as a measure of quantum coherence. Phys. Rev. A 92, 022124 (2015).
Ma, X. et al. Postprocessing for quantum random-number generators: Entropy evaluation and randomness extraction. Phys. Rev. A 87, 062327 (2013).
Jennewein, T., Achleitner, U., Weihs, G., Weinfurter, H. & Zeilinger, A. A fast and compact quantum random number generator. Rev. Sci. Instrum. 71, 1675–1680 (2000).
Stefanov, A., Gisin, N., Guinnard, O., Guinnard, L. & Zbinden, H. Optical quantum random number generator. J. Mod. Opt. 47, 595–598 (2000).
Rarity, J., Owens, P. & Tapster, P. Quantum random-number generation and key sharing. J. Mod. Opt. 41, 2435–2444 (1994).
Eisaman, M. D., Fan, J., Migdall, A. & Polyakov, S. V. Invited review article: Single-photon sources and detectors. Rev. Sci. Instrum. 82, 071101 (2011).
Takesue, H. et al. Quantum key distribution over a 40-db channel loss using superconducting single-photon detectors. Nat. Photon. 1, 343–348 (2007).
Patel, K. A. et al. Coexistence of high-bit-rate quantum key distribution and data on optical fiber. Phys. Rev. X 2, 041010 (2012).
Dynes, J. F., Yuan, Z. L., Sharpe, A. W. & Shields, A. J. A high speed, postprocessing free, quantum random number generator. Appl. Phys. Lett. 93, 031109 (2008).
Wayne, M., Jeffrey, E., Akselrod, G. & Kwiat, P. Photon arrival time quantum random number generation. J. Mod. Opt. 56, 516–522 (2009).
Wahl, M. et al. An ultrafast quantum random number generator with provably bounded output bias based on photon arrival time measurements. Appl. Phys. Lett. 98, 171105 (2011).
Nie, Y.-Q. et al. Practical and fast quantum random number generation based on photon arrival time relative to external reference. App. Phys. Lett. 104, 051110 (2014).
Ma, H.-Q., Xie, Y. & Wu, L.-A. Random number generation based on the time of arrival of single photons. Appl. Opt. 44, 7760–7763 (2005).
Yan, Q., Zhao, B., Liao, Q. & Zhou, N. Multi-bit quantum random number generation by measuring positions of arrival photons. Rev. Sci. Instrum. 85, 103116 (2014).
Fürst, H. et al. High speed optical quantum random number generation. Opt. Express 18, 13029–13037 (2010).
Ren, M. et al. Quantum random-number generator based on a photon-number-resolving detector. Phys. Rev. A 83, 023820 (2011).
Applegate, M. et al. Efficient and robust quantum random number generation by photon number detection. Appl. Phys. Lett. 107, 071106 (2015).
Sanguinetti, B., Martin, A., Zbinden, H. & Gisin, N. Quantum random number generation on a mobile phone. Phys. Rev. X 4, 031056 (2014).
Grosshans, F. et al. Quantum key distribution using gaussian-modulated coherent states. Nature 421, 238–241 (2003).
Braunstein S. L., & van Loock P . Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005).
Gabriel, C. et al. A generator for unique quantum random numbers based on vacuum states. Nat. Photon. 4, 711–715 (2010).
Shen, Y., Tian, L. & Zou, H. Practical quantum random number generator based on measuring the shot noise of vacuum states. Phys. Rev. A 81, 063814 (2010).
Symul, T., Assad, S. & Lam, P. K. Real time demonstration of high bitrate quantum random number generation with coherent laser light. Appl. Phys. Lett. 98, 231103 (2011).
Okubo, R., Hirano, M., Zhang, Y. & Hirano, T. Pulse-resolved measurement of quadrature phase amplitudes of squeezed pulse trains at a repetition rate of 76 mhz. Opt. Lett. 33, 1458–1460 (2008).
Chi, Y.-M. et al. A balanced homodyne detector for high-rate gaussian-modulated coherent-state quantum key distribution. New J. Phys. 13, 013003 (2011).
Kumar, R. et al. Versatile wideband balanced detector for quantum optical homodyne tomography. Opt. Commun. 285, 5259–5267 (2012).
Qi, B., Chi, Y.-M., Lo, H.-K. & Qian, L. High-speed quantum random number generation by measuring phase noise of a single-mode laser. Opt. Lett. 35, 312–314 (2010).
Jofre, M. et al. True random numbers from amplified quantum vacuum. Opt. Express 19, 20665–20672 (2011).
Xu, F. et al. Ultrafast quantum random number generation based on quantum phase fluctuations. Opt. Express 20, 12366–12377 (2012).
Yuan, Z. et al. Robust random number generation using steady-state emission of gain-switched laser diodes. Appl. Phys. Lett. 104, 261112 (2014).
Abellán, C. et al. Ultra-fast quantum randomness generation by accelerated phase diffusion in a pulsed laser diode. Optics Express 22: 1645–1654. (2014).
Nie, Y.-Q. et al. The generation of 68 gbps quantum random number by measuring laser phase fluctuations. Rev. Sci. Instrum. 86, 063105 (2015).
Williams, C., Salevan, J., Li, X., Roy, R. & Murphy, T. Fast physical random number generator using amplified spontaneous emission. Opt. Express 18, 23584–23597 (2010).
Li, X., Cohen, A. B., Murphy, T. E. & Roy, R. Scalable parallel physical random number generator based on a superluminescent led. Opt. Lett. 36, 1020–1022 (2011).
Henry, C. H. Theory of the linewidth of semiconductor lasers. IEEE J. Quant. Electron. 18, 259–264 (1982).
Zhou, H., Yuan, X. & Ma, X. Randomness generation based on spontaneous emissions of lasers. Phys. Rev. A 91, 062316 (2015).
Abellán, C., Amaya, W., Mitrani, D., Pruneri, V. & Mitchell, M. Generation of fresh and pure random numbers for loophole-free bell tests. Phys. Rev. Lett. 115, 250403 (2015).
Mayers, D. & Yao, A. in Proceedings of the 39th Annual Symposium on Foundations of Computer Science, FOCS 1998, 503–509 (IEEE Computer Society, Palo Alto, CA, USA, 1998).
AcÃn, A., Gisin, N. & Masanes, L. From bells theorem to secure quantum key distribution. Phys. Rev. Lett. 97, 120405 (2006).
Popescu, S. & Rohrlich, D. Quantum nonlocality as an axiom. Found. Phys. 24, 379–385 (1994).
Colbeck, R. Quantum and Relativistic Protocols for Secure Multi-Party Computation. PhD thesis, Univ. of Cambridge (2009).
Colbeck, R. & Kent, A. Private randomness expansion with untrusted devices. J. Phys. A Math. Gen. 44, 095305 (2011).
Clauser, J. F., Horne, M. A., Shimony, A. & Holt, R. A. Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969).
Fehr, S., Gelles, R. & Schaffner, C. Security and composability of randomness expansion from bell inequalities. Phys. Rev. A 87, 012335 (2013).
Pironio, S. & Massar, S. Security of practical private randomness generation. Phys. Rev. A 87, 012336 (2013).
Vazirani, U. & Vidick, T. Certifiable quantum dice: or, true random number generation secure against quantum adversaries. in Proc. Forty-fourth Annual ACM Symposium on Theory of Computing (ACM, New York, NY, 2012).
Miller, C. A. & Shi, Y. Robust protocols for securely expanding randomness and distributing keys using untrusted quantum devices. in Proc. Forty-sixth Annual ACM Symposium on Theory of Computing (ACM, New York, NY, 2014).
Chung, K.-M., Shi, Y. & Wu, X. Physical randomness extractors: Generating random numbers with minimal assumptions. Preprint at arXiv:1402.4797 (2014).
Miller, C. A. & Shi, Y. Universal security for randomness expansion. Preprint at arXiv:1411.6608 (2014).
Pironio, S. et al. Random numbers certified by Bell’s theorem. Nature 464, 1021–1024 (2010).
Giustina, M. et al. Bell violation using entangled photons without the fair-sampling assumption. Nature 497, 227–230 (2013).
Christensen, B. G. et al. Detection-loophole-free test of quantum nonlocality, and applications. Phys. Rev. Lett. 111, 130406 (2013).
Nieto-Silleras, O., Pironio, S. & Silman, J. Using complete measurement statistics for optimal device-independent randomness evaluation. New J. Phys. 16, 013035 (2014).
Bancal, J.-D., Sheridan, L. & Scarani, V. More randomness from the same data. New J. Phys. 16, 033011 (2014).
AcÃn, A., Massar, S. & Pironio, S. Randomness versus nonlocality and entanglement. Phys. Rev. Lett. 108, 100402 (2012).
de la Torre, G., Hoban, M. J., Dhara, C., Prettico, G. & AcÃn, A. Maximally nonlocal theories cannot be maximally random. Phys. Rev. Lett. 114, 160502 (2015).
Colbeck, R. & Renner, R. Free randomness can be amplified. Nat. Phys. 8, 450–454 (2012).
Pearle, P. M. Hidden-variable example based upon data rejection. Phys. Rev. D 2, 1418–1425 (1970).
Braunstein, S. L. & Caves, C. M. Wringing out better Bell inequalities. Ann. Phys. 202, 22–56 (1990).
Santha, M. & Vazirani, U. V. Generating quasi-random sequences from semi-random sources. J. Comput. Syst. Sci. 33, 75–87 (1986).
Gallego, R. et al. Full randomness from arbitrarily deterministic events. Nat. Commun. 4, 2654 (2013).
Mermin, N. D. Simple unified form for the major no-hidden-variables theorems. Phys. Rev. Lett. 65, 3373–3376 (1990).
Barrett, J. & Gisin, N. How much measurement independence is needed to demonstrate nonlocality? Phys. Rev. Lett. 106, 100406 (2011).
Koh, D. E. et al. Effects of reduced measurement independence on bell-based randomness expansion. Phys. Rev. Lett. 109, 160404 (2012).
Pope, J. E. & Kay, A. Limited measurement dependence in multiple runs of a bell test. Phys. Rev. A 88, 032110 (2013).
Pütz, G., Rosset, D., Barnea, T. J., Liang, Y.-C. & Gisin, N. Arbitrarily small amount of measurement independence is sufficient to manifest quantum nonlocality. Phys. Rev. Lett. 113, 190402 (2014).
Beaudry, N. J., Moroder, T. & Lütkenhaus, N. Squashing models for optical measurements in quantum communication. Phys. Rev. Lett. 101, 093601 (2008).
Cao, Z., Zhou, H., Yuan, X. & Ma, X. Source-independent quantum random number generation. Phys. Rev. X 6, 011020 (2016).
Shor, P. W. & Preskill, J. Simple proof of security of the bb84 quantum key distribution protocol. Phys. Rev. Lett. 85, 441–444 (2000).
Marangon, D. G., Vallone, G. & Villoresi, P. Source-device-independent ultra-fast quantum random number generation. arXiv:1509.07390 (2015).
Cao, Z., Zhou, H. & Ma, X. Loss-tolerant measurement-device-independent quantum random number generation. New J. Phys. 17, 125011 (2015).
Lunghi, T. et al. Self-testing quantum random number generator. Phys. Rev. Lett. 114, 150501 (2015).
Bowles, J., Quintino, M. T. & Brunner, N. Certifying the dimension of classical and quantum systems in a prepare-and-measure scenario with independent devices. Phys. Rev. Lett. 112, 140407 (2014).
Barak B., Shaltiel R. & Tromer E . Cryptographic Hardware and Embedded Systems-CHES 2003 166–180 (Springer, 2003).
Hensen, B. et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Shalm, L. K. et al. Strong loophole-free test of local realism*. Phys. Rev. Lett. 115, 250402 (2015).
Giustina, M. et al. Significant-loophole-free test of bell’s theorem with entangled photons. Phys. Rev. Lett. 115, 250401 (2015).
Ballance, C. et al. Hybrid quantum logic and a test of bells inequality using two different atomic isotopes. Nature 528, 384–386 (2015).
Gallicchio, J., Friedman, A. S. & Kaiser, D. I. Testing bells inequality with cosmic photons: Closing the setting-independence loophole. Phys. Rev. Lett. 112, 110405 (2014).
Canetti, R. in Proc. 42nd IEEE Symposium on Foundations of Computer Science. (2001).
Canetti, R & Krawczyk, H . Advances in Cryptology EUROCRYPT 2002. 337–351 (Springer, 2002).
Ben-Or M., Horodecki M., Leung, D. W., Mayers, D. & Oppenheim, J . Theory of Cryptography. 386–406 (Springer, 2005).
Renner, R., & König, R . Theory of Cryptography. 407–425 (Springer, 2005).
Trevisan, L. Extractors and pseudorandom generators. J. ACM 48, 860–879 (2001).
Raz, R., Reingold, O . & Vadhan S. Extracting all the randomness and reducing the error in Trevisan's extractors. in Proc. Thirty-first Annual ACM Symposium on Theory of Computing. (ACM, New York, NY, 1999).
De, A., Portmann, C., Vidick, T. & Renner, R. Trevisan’s extractor in the presence of quantum side information. SIAM J. Comput. 41, 915–940 (2012).
Uchida, A. et al. Fast physical random bit generation with chaotic semiconductor lasers. Nat. Photon. 2, 728–732 (2008).
Wegman, M. N. & Carter, J. L. New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 22, 265–279 (1981).
Mauerer, W., Portmann, C . & Scholz, V. B . A modular framework for randomness extraction based on trevisan’s construction. Preprint at arXiv:1212.0520 (2012)
Ma, X., Zhang, Z. & Tan, X. Explicit combinatorial design. arXiv:1109.6147 (2011).
Acknowledgements
The authors thank R. Colbeck, H.-K. Lo, Y. Shi and F. Xu for enlightening discussions. This work was supported by the National Basic Research Program of China Grants No. 2011CBA00300 and No. 2011CBA00301, the 1000 Youth Fellowship program in China and the Laboratory Directed Research and Development (LDRD) Program of Oak Ridge National Laboratory (managed by UT-Battelle LLC for the US Department of Energy)
Author information
Authors and Affiliations
Contributions
All authors contributed extensively to the work presented in this paper. X.Y. focused on the self-testing QRNG part. Z.C. focused on the semi-self-testing QRNG part. B.Q. and Z.Z. focused on the practical QRNG part. X.M. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ma, X., Yuan, X., Cao, Z. et al. Quantum random number generation. npj Quantum Inf 2, 16021 (2016). https://doi.org/10.1038/npjqi.2016.21
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/npjqi.2016.21
This article is cited by
-
Provably-secure quantum randomness expansion with uncharacterised homodyne detection
Nature Communications (2023)
-
Finite key performance of satellite quantum key distribution under practical constraints
Communications Physics (2023)
-
Resolution of 100 photons and quantum generation of unbiased random numbers
Nature Photonics (2023)
-
A comprehensive review of quantum random number generators: concepts, classification and the origin of randomness
Quantum Information Processing (2023)
-
A quantum random number generator on a nanosatellite in low Earth orbit
Communications Physics (2022)