Faceted interfaces: a key feature to quantitative understanding of transformation morphology

Abstract

Faceted interfaces are a typical key feature of the morphology of many microstructures generated from solid-state phase transformations. Interpretation, prediction and simulation of this faceted morphology remain a challenge, especially for systems where irrational orientation relationships (ORs) between two phases and irrational interface orientations (IOs) are preferred. In terms of structural singularities, this work suggests an integrated framework, which possibly encompasses all candidates of faceted interfaces. The structural singularities are identified from a matching pattern, a dislocation structure and/or a ledge structure. The resultant singular interfaces have discrete IOs, described with low-index g’s (rational orientations) and/or Δg’s (either rational or irrational orientations). Various existing models are grouped according to their determined results regarding the OR and IO, and the links between the models are clarified in the integrated framework. Elimination of defect types as far as possible in a dominant singular interface often exerts a central restriction on the OR. An irrational IO is usually due to the elimination of dislocations in one direction, i.e., an O-line interface. Analytical methods using both three-dimensional and two-dimensional models for quantitative determinations of O-line interfaces are reviewed, and a detailed example showing the calculation for an irrational interface is given. The association between structural singularities and local energy minima is verified by atomistic calculations of interfacial energies in fcc/bcc alloys where it is found that the calculated equilibrium cross-sections are in a good agreement with observations from selected alloys.

Introduction

The product phases generated from a solid-state phase transformation often display similar morphologies characterised by faceted interfaces. The major faceted interface of a plate- or lath-shaped product phase is usually referred to the habit plane (HP). Such a HP is generally associated with a unique reproducible crystallographic orientation with respect to both phases, which are usually related by a particular orientation relationship (OR). A quantitative description of a microstructure with faceted morphologies must include the crystallographic information, such as ORs, interface orientations (IOs) of facets, long axes of elongated morphologies, etc. Experimental characterisation of crystallographic information has been facilitated by advances in electron microscopy, especially the development of the electron backscatter diffraction technique.^1–3 Computer simulations of microstructures generated from solid-state phase transformations have also achieved a certain degree of success.^4–8 The orientations of the predicted faceted interfaces are a key parameter that can be used to check whether a simulated morphology actually resembles what is observed in a real material. Simulation results are generally in excellent agreement with experimental results if the two phases are related by a rational OR and have a rational HP.^9,10 (Here a rational OR means that the OR can be expressed in terms of parallelism of low-index planes and of low-index directions in two phases: otherwise, the OR is irrational. Similarly, a rational interface is parallel to low-index planes in both phases, and otherwise, the interface is irrational.) However, it remains a challenge to simulate a morphology that truly agrees with the experimental data when the morphology exhibits a Widmanstätten pattern with an irrational HP, as often observed in steels and Ti alloys.

Correct understanding and interpretation of crystallographic features is an essential basis for microstructure simulation and its control. While a rational HP appears reasonable, as it agrees with one’s expectation according to the facets in a crystal surface, why a HP prefers a particular irrational orientation has been a puzzling issue for more than half a century. Attempts to understand the irrational HPs of martensite have led to breakthroughs resulting from the development of the phenomenological theory of martensite crystallography (PTMC) in the early 1950s.^11–13 This theory remains applicable to most martensitic transformations and Wayman’s book¹⁴ on this topic still serves as the best comprehensive reference for this theory. However, faceted interfaces of precipitates are not necessarily subject to the glissile interface condition imposed by the PTMC theory.¹⁴ At the same time, many models have been developed for understanding the ORs and HPs of precipitates. The major models have been reviewed previously in detail in lengthy review papers.^15,16 More recently, Howe¹⁷ has provided an updated comprehensive review of major models in a book chapter.

In this paper, we focus on the faceted interfaces of precipitates, including those with either rational or irrational IOs. The paper combines useful concepts of various models from relevant studies, as well as insightful observations from numerous experimental results, to form an integrated approach for understanding faceted interfaces. The various models are sorted into groups, and links between them are clarified in the integrated framework. The contents of the first part are mainly descriptive, providing the basis for the computations described in the second part, which addresses analytical methods and atomistic simulations to determine the geometry of potential candidate irrational HPs and their associated ORs. Using the results from the analytical approach, atomistic simulations have been applied to provide an in-depth understanding of irrational, singular interfaces. It is hoped that this contribution will improve the quantitative understanding of transformation morphology, and will stimulate further research aimed at establishing better agreement between simulated microstructures and those in real materials.

Integrated framework

Background

Development of the OR between precipitate and matrix begins at the nucleation stage of a precipitate, when the interface geometry is free to vary. Nuclei with the OR corresponding to interfaces of low interfacial energy will survive, as interfacial energy is the major barrier to nucleation.¹⁸ To reduce the interfacial energy, an interface has a strong tendency to maintain coherency. Recent investigations of geometrically coherent (or coincidence site coherent) rational HPs with a combination of advanced electron microscopy and ab initio density functional theory have revealed the detailed structures of such interfaces.^19,20 Although specific interfacial structures may vary with phases, composition and even precipitate size, exact geometry matching in the interface is essential for a periodic low-energy structure to form. In a general system, perfect matching may not be maintained at the growth stage due to the presence of considerable misfit in real systems. However, local geometric matching is usually possible, so that low-energy structures can still be preserved in localised regions of an interface. Although a significant rotation in the OR is unlikely to occur at the growth stage, a small deviation in the OR is possible. With this degree of freedom (DOF), local matching can be sustained in interfaces at various local orientations. The question arises then as to why a particular OR and a unique orientation of HP is often preferred, particularly when one or both are irrational?

Observation of a HP or other faceted interfaces with a consistently reproducible orientation indicates that these interfaces are thermodynamically stable against any perturbation in the IO. Following the terminology of Sutton and Balluffi,²¹ a faceted interface must be a singular interface, whose interfacial energy exhibits a singularity feature at least with respect to the variation in the IO. When a faceted interface is also constantly associated with a unique OR, it must also be singular with respect to the OR. Even with powerful modern computing, it is impractical to search for candidate singular interfaces by exploring the variation of interfacial energy in the five degrees of boundary geometrical phase space for interfaces,²¹ where three DOF are needed to constrain the OR, and two more to constrain the IO. It is reasonable to assume, however, that a singularity in interfacial energy should correspond to a singularity in interfacial structure. Therefore, geometries for possible singular interfaces may be identified by searching for singularities in interfacial structure. The resultant candidates for singular interfaces may then serve as an input for further energy-based calculations and refinement.

A structural singularity is characterised by an abrupt change in certain interfacial features. This can be examined using two approaches. One approach is based on the structures of interfacial defects (ledges and dislocations). Here a specific arrangement of interfacial defects may be associated with a local minimum in interfacial energy. The other approach is based on patterns of match/mismatch (or fit/misfit) between lattice points at an interface. When perfect matching is impossible, a significant increase in matching may be associated with a corresponding drop in interfacial energy. Physically, one should evaluate matching between atoms, but local lattice matching is the essential geometrical condition to form a low-energy periodic structure in local regions of an interface, and it is much simpler to investigate matching between lattices. Quantitative analyses of interface singularity in these two approaches are described below.

Singularity based on matching patterns

Inspecting a pattern of the distribution of lattice matching is a very effective way to understand faceted interfaces, as demonstrated by the structural ledge model^22,23 and the near-coincidence sites (NCSs) model.²⁴ Let two lattices related by an arbitrary OR interpenetrate each other, as in the construction of an O-lattice or a coincidence site lattice (CSL).²⁵ Some lattice points from one lattice may be close to the points in the other lattice. To begin with, let us adopt first the good matching criterion suggested in the structural ledge model.^22,23 In this model, with a minor modification to generalise the criterion, a good matching site (GMS) is identified as a lattice point in the lattice with the larger unit cell (the larger lattice) when the distance from this point to a neighbouring lattice point in the other lattice is <15%|b_s| (where b_s is a Burgers vector of the lattice with the smaller unit cell). The GMS ratio (the number of GMSs with respect to the number of lattice points in the larger lattice) in a selected interface region is then used to evaluate the degree of matching in the interface. It has been found that the GMS ratios for a given system are almost constant with variation in the OR, unless exact CSLs can be defined.²⁶ The values of the ratios are discrete, approximately given by 30%, 7.5% and 1.5% for one-dimensional (1D), two-dimensional (2D) and three-dimensional (3D) misfit systems, respectively.

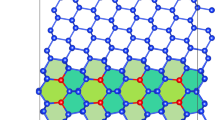
Figure 1 demonstrates the lattice matching between two 2D square lattices; GMSs are shown with larger green circles together with the atoms from the two lattices. The total ratios of GMSs in the plane of 2D misfit for Figure 1a, b are both ~7.5%. However, the GMSs in Figure 1a are randomly arranged, whereas the GMSs in Figure 1b form periodic clusters arranged in a regular array. Imagine now that the patterns in the figures extend without limit. No line in Figure 1a will pass obviously more GMSs than any other, but the horizontal or vertical line in Figure 1b, which goes through the centres of dense GMS clusters, will pass a significantly higher ratio of GMSs than any line in an adjacent orientation. Similarly, when two lattices in 3D are orientated with a random OR, the ratio of GMSs in an arbitrary interface is roughly only 1.5%. Such an interface is not singular according to matching features. As for a general large-angle grain boundary, its interfacial structure and energy are expected to be similar to that for an interface in its vicinal geometry. An interface that is singular according to matching features must be associated with a peak value of the GMS ratio. In other words, there should be a sudden drop in the GMS ratio in a vicinal interface. Therefore, the edge-on interfaces represented by the horizontal and vertical lines in Figure 1b are candidates of singular interfaces, if the 2D lattices in the figure are considered a projection of 3D simple cubic lattices. When the OR is random, the GMS ratio may vary less markedly. The interfacial plane normal to Δg (=g_α−g_β), where g_α and g_β are low-index reciprocal vectors, will contain GMSs with a relatively high ratio (i.e., ~7.5%>~1.5%), as interfacial misfit in the plane is virtually in 2D, lying on the planes defined by g_α and g_β. This geometry has been observed by Howe et al.,²⁷ who showed the association of faceted interfaces with denser NCS (equivalent to the term of GMS used here) when the OR is random. At the other extreme, an exact one-to-one matching or a CSL with small unit cell may form in 2D. As each point in a CSL is a point of GMS, the GMS ratio in the plane of dense CSL points will reach a peak value. Such a plane of ideal matching is undoubtedly a candidate for singular interfaces, in agreement with many observations.^19,20,28

Figure 1

GMS distribution for two square lattices at (a) an arbitrary OR and (b) a square-to-square OR, with the ORs shown in the insert on the top left. The open and filled small circles represent lattice points in different lattices; large circles represent GMSs. Lines represent edge-on interfaces, showing no singular interface in a and a singular interface along the horizontal line passing the GMS clusters in b.

The above ideal matching structures exist only when both lattice parameters and OR are special. In a general system, a periodic pattern of GMSs may sustain locally in the form of clusters, and the clusters will repeat due to the periodic nature of both lattices in 3D, as seen in Figure 1b. When the GMSs within a cluster are sufficiently dense in a real system, the periodic GMSs in the cluster may relax into a periodic (with small strain) stacking of small structural units, as described by Sutton and Vitek.²⁹ This localized periodic structure will probably serve as the reference structure preserved between dislocations, which is called a favoured boundary by Sutton and Vitek,²⁹ and a preferred state by Bollmann.^25,30 The term of preferred state will be followed in this paper. The association between the GMS clusters and the locations of the preferred state implies potential dislocations between the GMS clusters. A pair of adjacent GMS clusters is termed as intimate GMS clusters, if they are separated by one dislocation. Singularities based on GMS patterns will be consistent with those based on the dislocation structure considered in the following section, only if the interface passes two rows of intimate clusters. Such a plane will contain GMSs at a higher ratio than a plane in a vicinal orientation, and hence this plane is a candidate for singular interfaces.

According to the association between GMS clusters and dislocations models, the good matching criterion has been extended to a range of 15~25%|b_s|,³¹ as suggested by the well-known transition angle of 10~15° between small-angle grain boundaries (semi-coherent) and large-angle boundaries (incoherent). If no GMS clusters are found using a criterion of 15%|b_s|, a criterion of 25%|b_s| should be employed instead to allow for more candidate singular interfaces. If GMS clusters exist using a criterion of 15%|b_s|, an increase in the criterion does not affect the distribution of the cluster centres, but does lead to an expansion in the size of the clusters. In such cases, it is better to use the lower bound of 15%|b_s| to avoid possible overlap of clusters, as explained below.

Although the range of good matching criterion carries a certain degree of uncertainty, this uncertainty does not diminish the usefulness of the GMS cluster patterns as a guide to the identification of singular interfaces, and to indicate the preferred state and Burgers vector of the potential dislocations. Suppose that each cluster corresponds to a region where a preferred state is sustained, a unique linear correspondence must hold between the points in any good matching pair within a GMS cluster, and this condition restricts the scope of a GMS cluster. There is a relative shift between the correspondences in different clusters. The shift vector between the correspondences in intimate clusters is the Burgers vector of the potential dislocation between the clusters. A one-to-one good matching correspondence in a GMS cluster corresponds to the primary preferred state (the coherent state).²⁵ To maintain equivalent coherent structures in adjacent regions relaxed from intimate clusters, the Burgers vector of the dislocation separating the regions must be a small lattice translation vector of either lattice. Then, the GMS clusters will never overlap, as the misfit near a dislocation core is ~50%|b_s|. When good matching correspondence holds only between partial points within a cluster, a secondary preferred state (coincidence coherent state) may be developed from a 2D GMS cluster.²⁵ As explained in the CSL/DSC theory,^30,32 the Burgers vectors of the secondary dislocations between intimate GMS clusters must be from a DSC lattice (here DSC is a term for complete pattern shift as suggested by Bollmann³⁰). When the good matching criterion of 25%|b_s| is used, adjacent GMS clusters will meet if the DSC vector for the dislocations between the clusters is smaller than |b_s|/4. This probably sets a minimum size of DSC vectors for a distinguishable secondary dislocation, and hence the presence of well-separated GMS clusters may be regarded as the validity condition for a secondary dislocation model or a CSL/DSC model.

Singularity based on defect structures

The singularity in a defect structure is specified in terms of complete elimination of one or more types of defects.³³ An interfacial defect is defined with respect to a relatively ‘perfect structure’ of lower energy in the interface. The ‘perfect structure’ between ledge defects is an atomically flat terrace. A singular interface based on the ledge structure is among low-index planes in the corresponding crystals, similar to a singular surface. To satisfy this singularity condition in both lattices, the singular interface must be parallel to low-index planes in both phases. There remains one DOF in the OR to specify the in-plane rotation. Coexistence of other ledge-free facets will constrain the OR, e.g., the cube-to-cube OR in a TiN/Ni system.³⁴ This usually implies parallelism of a pair of vectors, lying on two rational facets. The selection of the OR is often affected by the preference for better matching, as seen with many rational coherent HPs.^19,20,28 It is also possible that a singularity in ledge defects holds with respect to only one crystal. Then, the interface may be singular only with respect to one crystal, with a preferred OR³⁴ or without a preferred OR.³⁵ Although singularity in ledge defects can explain observed rational HPs or facets, it cannot explain frequently observed irrational ones, which must contain ledges at the atomic scale. However, following the same principle, weak singularity caused by eliminating kinks in ledges may have a role in the development of irrational faceted interfaces.

An irrational HP or facet is governed by singularity in the dislocation structure, as well as in the good matching pattern. As stated previously, the reference structure between the dislocations is the structure of a preferred state relaxed from a GMS cluster. In general, singularity in the dislocation structure is characterised by minimum types of dislocations in a singular interface, such that a small deviation from the singular interface will introduce one or more additional types of dislocations. It implies a condition that the interfacial misfit in a singular interface is fully accommodated by misfit dislocations, and hence the effect of strain energy on the geometry of the singular interface is neglected. In this condition, it is rather straightforward to identify the singular interfaces in the framework of the O-lattice theory, which is well known for calculating dislocation structures in interfaces.^25,30 An O-lattice element may be a point, a line or a plane.^25,30 Each O-lattice element, being free of misfit, must locate at the centre of a GMS cluster. The principal O-lattice planes (POPs) are a set of special planes in the O-lattice. The interface parallel to a POP may contain a single O-plane, being free of dislocations; it may contain a set of O-lines with a single set of dislocations in between; or it may contain periodically distributed O-points separated by two or three sets of dislocations. Any deviation of an interface from the orientation of a POP will lead to introduction of one or more additional types of dislocations in the interface, in agreement with the singularity condition. Therefore, the POPs are candidates for singular interfaces.^15,25 It is convenient to express the orientation of a POP with a reciprocal vector, Δg.³⁶ The associated g must be related by the lattice correspondence and contain two Burgers vectors. Therefore, the total number of POPs for a given OR is limited, usually less than 10. An O-line interface is normal to a group of Δg’s³⁷ (Δg parallelism rule II¹⁵), and an O-plane, as an invariant plane, is normal to all Δg’s.³⁸ Thus, the IO of the interface is fixed. The Δg parallelism condition associated with the elimination of dislocations also restricts the OR, namely, two of the three DOF in the OR for an O-line interface, and all three DOF in the OR for an O-plane is fixed, as it is for a coherent interface.^19,20,28

An advantage of describing the IO in terms of Δg’s is that the Δg vectors are directly measurable. Observations of a HP being normal to a group of Δg’s were first reported by Dahmen in terms of diffraction spot splitting.³⁹ Figure 2 shows an example in which the HP between austenite (fcc) and ferrite (bcc) phases in Figure 2b is normal to the parallel Δg’s in Figure 2a. As shown by the parallel Δg’s, this HP must be an O-line interface.⁴⁰ Generally, elimination of dislocations is possible only at the expense of adding ledges, so the interface has an irrational IO. Numerous observations indicates that close-packed directions tend to align parallel in the interface,¹⁷ as also in Figure 2. With this constraint, the geometry for the interface is fixed and solvable, as seen in the section on the O-line model.

Figure 2

HP between the bcc matrix and a fcc precipitate in a duplex stainless steel. (a) Superimposed diffraction pattern, with parallel Δg’s indicated by line segments. (b) TEM image of the edge-on HP, normal to the Δg’s. (c) HRTEM image from a local HP in b, with edge-to-edge matching planes marked.

Integrated considerations

Figure 3 is an illustration of the integrated framework consisting of possible combinations of the three types of singular features, namely, matching patterns, ledge and dislocation arrangements. Interfaces with a particular singular feature are confined to a certain region in the figure. Consequently, if an interface is located in a zone that belongs to different regions, this interface will contain the singular features represented in these regions. The correspondences between the regions and singular features are the following. Interfaces exhibiting singularity in matching patterns are located within in the square region (surrounded by a dark-green line), denoted by M-square. Interfaces characterised by singularities in the dislocation structures are located within the circle and rings (bordered by brown circles), denoted by D₀, D₁ and D_>1, corresponding to zero, one and more than one set (i.e., two or three sets) of dislocations, respectively. All dislocation regions are enclosed in the M-square, as an interface governed by the dislocation singularity must also pass the centres of periodic GMS clusters. Interfaces that are free of ledges are located within a region enclosed by a blue solid circle and denoted by L_f. Those that contain kink-free ledges are located in a ring between blue circles with solid and dashed lines and denoted by K_f. Individual zones corresponding to different combinations of defect arrangements are coloured or given different shades of grey for convenience of discussion. The zones in this figure possibly encompass all the possible candidates for faceted interfaces. Regardless of which singular feature dictates the development of a faceted interface, an interface in any zone is singular with respect to the IO, and it has a discrete IO (with details given below). Although each singular feature may be a governing feature, the singular features tend to be realised simultaneously, and the types of defects tend to be eliminated as far as possible. In general, coexistence of singular features exerts restrictions on the OR and even on the lattice parameters. The fewer the defects in an interface, the less the unconstrained DOF in the interface geometry.

Figure 3

Illustration of singular features represented by different regions within a square, rings and circles: D₀-circle, zero set of dislocation; D₁–ring, one set of dislocations; D_>1–ring, more than one set of dislocations; L_f–circle, ledge-free; K_f-ring, kink-free ledges; M-square, matching pattern.

As discussed in the previous subsection, the OR corresponding to a structure in the D₁ ring or D₀ circle in Figure 3 is constrained by one or more Δg parallelism rules, with the faceted interface normal to the corresponding Δg(’s).¹⁵ The ORs for the interfaces in the red, light-blue, blue and green zones are limited by at least two rules. The corresponding interfaces are fully singular in the five degrees of boundary geometrical phase space, but this is only possible with particular lattice parameters.¹⁵ The ORs for the interfaces in the other coloured zones are constrained by one rule plus a pair of parallel low-index vectors. The OR for such an interface is also completely fixed, and can be determined with a 2D model in the plane normal to the parallel vectors. In general, overlap of the D_>1 ring and the K_f ring does not fix the OR, but the pink zone corresponds to a special one-to-one association between a ledge and a (secondary) dislocation, which also fully constrains the OR.¹⁵ Only two of the three DOF for the OR is fixed for an interface in any grey zone. The OR for an interface in the light- and mid-grey zones is confined by one Δg parallelism rule, and in the dark-grey zones is restricted by parallelism of two low-index vectors. An interface in the remaining white zones enclosed by a solid line is singular only with respect to the IO, described by either g or Δg, with a given OR. Generally, whenever the OR is reproducible, a singularity in the dislocation structure must be a governing feature; the interface will be normal to at least one Δg, with the associated g being normal to the Burgers vectors of the dislocations. Preference order among interfaces in different zones may be roughly estimated within the same defect zone. For example, within the D₀ circle, the preference order may red, light-blue and blue zone. Within the L_f circle, the preference order is red, green and yellow or light-grey, dark-grey and finally the white zone. In the D₁ ring, the preference order is green, orange or mid-grey zone.

Empirical knowledge often indicates the preferred tendency for certain interfacial structures in a given system, providing a helpful guide for narrowing the searching range in the application of the singularity approach. A preferred state has a strong tendency to form, and hence a singularity in the dislocation structure usually has a role in the development of faceted interfaces. This limits the OR to those that allow GMS clusters to form. In addition, singular interfaces following two rules will likely be realised in a system where the required special lattice parameter condition is satisfied. Whenever it is allowed by the lattice parameters, the primary preferred state is often preferred, which greatly restricts the possible range of the OR. A well-known example is the Bain correspondence, applicable to numerous alloys consisting of fcc and bcc simple metallic phases.¹⁴ The range of allowed ORs for a secondary preferred state is usually much narrower than the one for the primary preferred state, analogues to the range set by the Brandon criterion for the range of Σ grain boundaries.⁴¹

The selection among zones and constraints to the remaining degree(s) of freedom may be influenced by various factors. These include the structure of the two phases, possible segregation of elements, possible existence of a long-range strain, the temperature at which the interface is formed, the freedom for an interface to change its geometry, the driving force and the time allowed for the interfacial geometry to vary, and the kinetic properties of the interfaces. The weights of these influencing factors vary from one system to another. A complex combination of various factors leads to a variety of faceted interfaces and associated ORs in real materials, even for the same precipitates formed under different conditions (e.g., temperature and impurity level). Some of these factors affect the chemical component of interfacial energy. Although this effect was neglected in the above singularity analysis, its influence is implicatively included in the singularity in the ledge structure and matching pattern. This component usually favours a ledge-free singular interface. Its influence is likely to be strong when the system consists of a ceramic phase, and weak when the system consists of simple metallic phases. As a result, a singular interface tends to be free of ledges in ceramics, whereas irrational faceted interfaces often exist in metallic materials. Except in the white zone within the L_f circle, which corresponds to ledge-free interfaces independent of OR, all potential singular interfaces in Figure 3 lie within the M-square. Therefore, they are all governed by optimum matching, which has been a major argument used in many successful models. Dividing the M-square into specific zones according to structural singularities is helpful to clarify the links between these models. A detailed discussion is given in the following section.

Links between models

The links between various models stem from their common assumption that low interfacial energy governs the interfacial preference. Most models are based on analyses using certain parameters or conditions to find optimum matching or equivalently minimising misfit. Only a few investigations have involved calculation of the interfacial energy of interfaces with limited interface geometries.¹⁷ Each model is capable of predicting certain geometric features and explaining the corresponding experimental results. It is helpful to discuss different models by assigning them to groups according to their calculated results. On the basis of whether a model determines the OR, the IO for a given OR or the IO and OR together, the model is assigned to the OR group, the IO group and the IO+OR group, respectively. The major results of these models can be found in various zones in Figure 3, so that the links between the models can be visualised using this integrated framework.

The entire extent of the OR can be explored using models in the OR group. According to the symmetry-dictated criterion given by Cahn and Kalonji,⁴² an observed OR showing parallelism of common symmetry axes is associated with a symmetry-dictated energy minimum. Such an OR usually permits coexistence of rational faceted interfaces. The faceted interfaces are singular in terms of the ledge-free structure, and they are probably also singular in dislocation structure, i.e., in different zones within the L_f circle in Figure 3. An ideal coherent structure in the red zone in Figure 3 must fulfil the criterion of symmetry-dictated energy minimum, as the symmetry of two planes must be the same when a perfect matching structure forms in the interface parallel to these planes. This criterion does not deal with misfit between lattices, and it cannot explain irrational ORs. In contrast, the approach by Ikuhara and Pirouz identifies the preferred OR based on misfit evaluated according to the overlapping volume between reciprocal lattice spheres.⁴³ This approach has been extended by Gautam and Howe, who investigated preferred ORs according to the maximum total overlapping diffraction intensity.^44,45 Both approaches tend to favour a OR that permits the existence of a GMS cluster around the origin in reciprocal space. This geometry should be equivalent to the existence of GMS clusters in direct space, which is a crucial condition for the development of a preferred state that is essential for a dislocation model. Thus, the resultant ORs are likely to be enclosed within the dislocation circle and rings in Figure 3. A cubic-to-cubic OR was found in several fcc/fcc alloys based on this approach, and the low-energy interfaces were determined using the Δg approach.⁴⁵ These interfaces lie in the yellow zone, due to overlap of the D_>1 ring and the L_f circle.

The IO group contains several models. In some models, the measured ORs have been taken as the input for interpretation of the observed HPs, often in irrational IOs. The primary preferred state is usually assumed in a misfit analysis. The 3D invariant line (IL) model proposed by Luo and Weatherly⁴⁶ falls in this group. They determined the HP according to two vectors in the interface plane: an approximate IL and another vector of small misfit. The structural ledge model proposed by Aaronson and his colleagues,^22,23 and the NCS model developed by Liang and Reynolds²⁴ are also in this group. According to the structural ledge model, an irrational HP containing structural ledges is preferred, as it exhibits a higher overall GMS fraction than the interface parallel to atomic flat planes in both phases.^22,23 According to the NCS model,²⁴ a HP should lie along the greatest area passing an array of continuous NCSs (i.e., GMSs). All three models above were applied to interpreting HPs in an fcc/bcc system with the K–S OR. The observed OR usually incorporates a small experimental uncertainty. If a nearby OR (i.e., <0.5° rotation around parallel Burgers vectors) corresponding to an O-line condition is used as an input, all these models yield a HP containing the O-lines, typically in the orange zone in the D₁ ring in Figure 3. This O-line interface fulfills the condition of the 3D IL model,⁴⁶ and contains periodic GMS clusters extended indefinitely along an IL crossing ledges, in agreement with the structural ledge model and the NCS model.²⁴ As indicated earlier, the preference order applies only within the same defect zone. In general, a ledge-free interface is not necessarily less preferred than an interface in the D₁ ring, although the GMS ratio in the latter is much higher. A model proposed by Knowles and Smith⁴⁷ identified the HP with given ORs according to a criterion of minimum dislocation content. The concept of a Burgers content ellipse suggested in this method is particularly useful for a systematic analysis of misfit distribution, and has stimulated further development along similar lines.^48–50 This approach can predict the shape of a single GMS cluster. However, the large dimension of a GMS cluster may or may not coincide with a row of dense GMS clusters.⁵⁰ Because it disregards the dislocation distribution, this approach is more suitable for a misfit analysis at a coherent stage.⁵⁰ The IO group also contains the faceted interfaces that are not singular with respect to the OR. An example is the faceted interfaces observed from a ZrN/Zr system.³⁵ Such interfaces are parallel to a low-index plane in ZrN and free of ledges, but interfacial matching is poor and ORs are not reproducible. These kinds of ledge-free interfaces are in the white zone within the L_f circle in Figure 3. Faceted interfaces due to a massive phase transformation²⁷ are associated with a singularity in GMS pattern, but they are not singular with respect to the OR. These facets locate in the white zone in the M-square in Figure 3. Such an interface is characterised by a one-dimensional commensurate structure.²⁷ Its association with a local energy minimum has also been confirmed with an energy calculation.⁵¹

The IO+OR group contains numerous models. These are all geometric models, with detailed misfit analysis according to certain optimum conditions. A preferred state, normally the primary preferred state, is usually implied for the misfit evaluation. This limits the range of changes in the OR, such that a GMS cluster corresponding to the preferred state must exist. With the preferred state being the reference for the dislocation structures, the corresponding singular interfaces must be within the dislocation circle or rings in Figure 3. A pioneering approach proposed by Bollmann and Nissen⁵² assumes a monotonic correspondence between interfacial energy and a parameter that is a function of dislocation spacing and Burgers vectors. They derived the OR that corresponded to the minimum values of this parameter. This method was modified by Ecob and Ralph⁵³ and Knowles and Smith.⁴⁷ The optimum interfaces from these parameter approaches are usually parallel to the POPs,^52–54 as one or more types of dislocations will be added to any vicinal interface, causing the value of a parameter to increase. These optimum interfaces are singular interfaces within the dislocation rings in Figure 3. The above approaches further narrow the candidates to particular POPs associated with the smallest value of the selected parameters.

Many models for an irrational HP are associated with the existence of an IL. Accumulating evidence for irrational HPs supports the existence of an IL in the HP.^55–60 The IL condition alone does not restrict an interface plane. When a faceted interface is observed, it usually contains a single set of dislocations lying along the IL, i.e., in the D₁ ring in Figure 3. This condition does not fix the OR and the IL. A method for calculating the geometry of interfaces in the D₁ ring is provided in the section covering the O-line model. Many existing models also add the constraint of a pair of low-index vectors been parallel, so that the OR is fixed. Various models to determine the OR and the HP can be divided to two subgroups, one aimed at deriving the geometry of the IL and the other emphasising the role of ledges crossed by an IL. In the first subgroup, the 2D IL model proposed by Dahmen⁵⁶ is a pioneer study. It has led to a breakthrough in the understanding of irrational features associated with precipitates, as an IL is usually in an irrational orientation and the required OR is also usually irrational. Using this model, the OR and the HP can be calculated with simple matrix algebra.^56,61 When the parallel vectors are close-packed directions, which must be the Burgers vectors of the dislocations, as is often the case, the corresponding interface locates in the orange zone in the D₁ ring in Figure 3. Formulas for the geometry of such a singular interface can be found in the section covering the O-line model.

The above special condition for the HP in the orange zone in Figure 3 has been adopted by a number of independent 2D models, in terms of cancellation between misfit associated with the terraces and ledges, to which an irrational HP can be resolved in an atomic scale. Figure 4 shows a comparison of exact matching between planes along an IL and locally distorted matching in a resolved HP.⁶² These models include an analysis to explain the structural ledges in terms of pattern advance by Van der Merwe et al.^63–66 and the topological model emphasising the role of disconnections (ledges) by Pond and colleagues.^67–69 The IL must be normal to the parallel Burgers vectors, if the misfit cancellation is evaluated between lattice points or atoms. This restriction is removed if the cancellation or matching is evaluated in terms of atom rows or plane edges. This approach was pioneered by Frank in an early study of the irrational HP of martensite.⁷⁰ The edge-to-edge matching model proposed by Kelly and Zhang provides interpretation of the OR and HP with a systematic analysis,^71,72 which is also applicable to systems in a secondary preferred state. The structure of edge-to-edge matching between planes is ensured in an O-line interface, as can be explained with Δg parallelism rule II. This can be seen in the high-resolution transmission electron microscopy image of the HP in Figure 2c, where fine lines representing edge-on planes have been drawn to guide observation of the plane matching (also see from illustrations in Figures 4a, 5a and 6d). When the lattice parameter is appropriate, the O-line condition can be realised exactly in a low-index plane interface, i.e., in the green zone in Figure 3. This interface structure exhibits exact row matching, whose geometry is confined by a row matching condition in reciprocal space specified by the Δg parallelism rules I and II. A row matching structure has been proven to be associated with an energy cusp based on a systematic energy calculation for various interfaces between an epitaxial layer and a substrate.⁷³ More details about row matching approaches can be found in a book chapter by Howe.¹⁷ Approximate row matching may also be realised by a local relaxation in an O-line interface (Figures 2c and 4b). Its association with an energy cusp in five degrees of boundary geometrical phase space is confirmed by an energy calculation in the final section. This is possibly why such a particular irrational HP is often observed.

Figure 4

An edge-on interface in a along an IL in a high-index direction u, showing no misfit along the IL In b, the IL is resolved into every close-packed plane as in an fcc/bcc transformation. Reproduced from Figure 4b and 4d in a paper by Dahmen with permission from Elsevier.⁶²

Figure 5

Geometry of the O-line interfaces. (a) End-to-end matching of dense atomic rows at an O-line interface ABC (different lattice points in different colours); (b) orientations of O-line interfaces confined in an elliptical cone (blue). The potential ILs defined by the initial un-extended cone are also plotted. The OR is specified by the angles, δ, between Burgers vectors.

Figure 6

An illustration of an O-line interface (HP) in a fcc/bcc system with ${\left[01\overline{1}\right]}_{\mathrm{f}}//{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}$. (a) simulated electron diffraction pattern at initial Pitsch OR; (b) simulated diffraction pattern at an O-line OR that is 0.44° from the exact K–S OR, with the HP trace normal to the parallel Δg’s; (c) matching structure of the HP in the plane view; (d) matching structure of the HP in an edge-on view along ${\left[01\overline{1}\right]}_{\mathrm{f}}//{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}$.

Faceted interfaces in a secondary preferred state also show a strong tendency for exact row matching, when allowed by the lattice parameters,^74,75 as in the green zone in Figure 3. Most, if not all, irrational faceted interfaces in a secondary preferred state contain parallel low-index directions. These interfaces exhibit approximate row matching in the terraces containing GMS clusters. The misfit between rows is cancelled by the displacement associated with the ledges, which may be treated as secondary dislocations,^76–78 separating the regions of the secondary preferred state in the terraces. The corresponding interfaces are contained in the pink zone in the D_>1 ring in Figure 3. They are different from irrational interfaces in the primary preferred state, where the ledges crossed by an IL are contained within one GMS cluster. Whereas, the GMS clusters in an interface in a secondary preferred state are discontinuous at ledges, since the ledges could be treated as secondary dislocations. The condition of good matching between rows, also in addition to good matching within the row, has been used in a systematic search for potential secondary preferred states that appears consistent with the observation of multiple ORs in an Mg–Sn system (W.-Z. Zhang et al., unpublished data).

An interface containing a set of dislocations in the primary preferred state may not always contain any low-index direction, i.e., may lie in the mid-grey zone in Figure 3. Although the corresponding ORs are infinite, two of the three DOF for the OR are restricted. A method of calculating a full set of O-line interfaces with a 3D model^79,80 will be reviewed in the following section, together a revised 2D method.⁸¹ This 2D model also provides the configuration of the dislocations. Unless the IL is normal to the Burgers vector, the dislocation calculation method is not possible with other 2D models.

O-line model

In this section, the calculation methods for the OR and IO of the HP containing O-lines will be presented based on O-lattice theory^25,30,82 and O-line properties. An interface that contains O-lines is called an O-line interface. For simplicity, the primary preferred state is assumed, but the calculation methods are readily extendable to systems in the secondary preferred state. In particular, the geometry required satisfying cancellation between the misfit displacement associated with ledges and that in the terraces can be determined with an extended 2D O-line model.⁸¹ The methods for solving O-line interfaces have evolved from the initial numerical approach³⁷ to analytical approaches.^79,80 The more advanced analytical approach will be given below for 3D and 2D models, respectively.

3D O-line model

Calculation of the O-lines in 3D is mainly based on three properties of the O-line interfaces. Two of them were extended by Zhang and Purdy³⁷ based on the properties of general ILs given by Bowles and Mackenzie in their work on the PTMC¹¹ and on similar properties in the O-lattice theory.²⁵ The other one was summarised more recently by Gu et al.^80,83 These properties are described briefly below.

Property 1

Both Burgers vectors, $\mathbf{b}\mathrm{\alpha }\mathrm{L}$ and $\mathbf{b}\mathrm{\beta }\mathrm{L}$, defined in different lattices, α and β, for the dislocations between the O-lines should be normal to the invariant normal, $\mathbf{x}\mathrm{IL}*$, namely,^11,37

$$\begin{array}{}\text{(1)}& \mathbf{x}\mathrm{IL}*\prime \mathbf{b}\mathrm{\alpha }\mathrm{L}=\mathbf{x}\mathrm{IL}*\prime \mathbf{b}\mathrm{\beta }\mathrm{L}=0\end{array}$$

Equation (1) is the key constraint restricting the O-line transformation strain. Any direction confined to the un-extended cone in reciprocal space can be rotated to become an $\mathbf{x}\mathrm{IL}*$.¹⁴ The $\mathbf{x}\mathrm{IL}*$ for an O-line interface is fixed for a given Burgers vector according to Equation (1). However, there are still numerous ORs satisfying the O-line criterion by small rotations around this $\mathbf{x}\mathrm{IL}*$.^37,79 A candidate for the HP, as an O-line interface, can be determined corresponding to each OR.

Property 2

An O-line interface should be normal to a set of Δg’s, with the connected g_α and g_β obeying the following conditions, ${\mathbf{g}}_{\mathrm{\alpha }}\text{'}\mathbf{b}\mathrm{\alpha }\mathrm{L}={\mathbf{g}}_{\mathrm{\beta }}\text{'}\mathbf{b}\mathrm{\beta }\mathrm{L}=0$. The planes defined by the related reciprocal vectors of g_α and g_β should match edge-to-edge at the interface, and the misfit should lie in g_β plane. Since the interface is normal to a set of Δg’s, any misfit in the interface must lie along the zone axis of the matching planes, i.e., along the Burgers vector in either lattice. Depending on the lattice parameters, the parallel Δg’s usually have an irrational orientation with respect to both lattices. This property can be seen from the lattice image in Figure 2c.

Property 3

Dense atomic rows along the correlated Burgers vectors of the dislocations should match in an end-to-end manner (Figure 5a) at an O-line interface, unless the Burgers vectors are parallel, in which case they must lie in the interface plane. This is because any misfit displacement vector must be along either Burgers vector.^83,84 The end-to-end matching geometry of rows is consistent with the prism matching condition proposed by Bilby and Frank in an early study of martensite crystallography.⁸⁵

As seen in Figure 5a, when the OR is changed by a rotation around the invariant normal, which is normal to both Burgers vectors (Equation (1)), the row matching condition is maintained, but the IO is altered. On the basis of this geometry, analytical expressions for ORs, the IO and the configuration of the dislocation structures in the HPs have been derived.⁸⁴ It is found that the HP orientations must be confined in an elliptic cone. Such an elliptic cone for an fcc/bcc system is shown in Figure 5b, together with the directions of the ILs. The corresponding ORs are defined with the angle, δ, between the related Burgers vectors. These data provide IO inputs for systematic study of the interfacial energies of O-line interfaces.^86,87

The essential inputs for an O-line calculation are the Burgers vector of the dislocations and an initial misfit strain A_o. To specify A_o, the lattice parameters, a tentative input of the OR (usually the measured one), and a proper lattice correspondence for the ideal good matching must be known. The lattice correspondence can be determined according to the correlation between points in good matching pairs in the centre GMS cluster. The principal strain B, e.g., the Bain strain for an fcc/bcc system, can be obtained by diagonalising A_o^1/2′A_o^1/2. The basic analytical method is borrowed from the PTMC,¹⁴ which provides the equation for the un-extended cone based on B. On this cone, usually two equivalent solutions for the possible invariant normal can be derived using Equation (1). As shown in Figure 5b, numerous O-line interfaces can be determined for a specific invariant normal. Free software called PTCLab, which is available at https://sourceforge.net/projects/tclab/,⁸⁸ can be used to calculate O-line interfaces in a general system. A further additional constraint must be imposed to restrict the solutions. In contrast to the dislocation glissile condition in the PTMC,¹⁴ a common constraint for a precipitation system is parallelism of the Burgers vectors. With this special condition, the O-line interface can be determined in a 2D model, as presented below.

2D O-line model

When the related Burgers vectors are parallel, a 2D analysis can be carried out in the plane normal to the parallel vectors. By extending Dahmen’s 2D model,⁵⁶ Wu et al.⁸¹ proposed a 2D calculation method in reciprocal space to perform such an analysis. While the OR and normal of the HP can be determined by many other 2D models,^71,72,89,90 this new method can yield additional information about the dislocation structures in the HP. An example of using this model is given in Figure 6a, which shows a superimposed diffraction pattern along ${\left[01\overline{1}\right]}_{\mathrm{f}}//{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}$ at the Pitsch OR in an fcc/bcc system with lattice parameters of a_f=0.3639 nm and a_b=0.2898 nm for the fcc and bcc phases, respectively. Like the model in direct space proposed by Xiao and Howe,⁶¹ with a selection of a proper initial OR and coordinates a general initial transformation matrix in 2D reciprocal space can be represented by:⁸¹

$$\begin{array}{}\text{(2)}& \mathbf{A}0*=\left[\begin{array}{cc}a& 0\\ s& b\end{array}\right]\end{array}$$

The transformation matrix in reciprocal space for the IL strain is given by A^*=RA₀^*, where R is an anticlockwise rotation in the 2D plane with the rotation angle, θ, defined by:⁸¹

$$\begin{array}{}\text{(3)}& \sin \theta =\frac{-s(1+ab)\pm (a+b\sqrt{s^2-(a^2-1)(b^2-1)})}{{(a+b)}^2+s^2}\end{array}$$

The invariant normal is solvable only when s²⩾(a²−1)(b²−1). In such a case, the HP normal is then simply defined by

$$\begin{array}{}\text{(4)}& \mathbf{n}=[b\sin \theta 1-b\cos \theta ]\end{array}$$

General expressions for the direction and spacing of the dislocations have been derived for a given Burgers vectors in the HPs of both fcc/bcc and bcc/hcp systems.^81,91 The direction of the IL can be specified by an anticlockwise rotation angle, ω, with respect to the parallel Burgers vectors. For the Burgers vector of ${\left[01\overline{1}\right]}_{\mathrm{f}}//{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}$, the angle ω and spacing of the parallel dislocations (D_dis) can both be expressed as function of the lattice parameters a_f and a_b, as given below:⁸¹

$$\begin{array}{}\text{(5)}& \sin \omega =\frac{2\sqrt{3}{a}_{\mathrm{f}}-3\sqrt{2}{a}_{\mathrm{b}}}{2\sqrt{6}{a}_{\mathrm{b}}-3a_{\mathrm{f}}}\end{array}$$

and

$$\begin{array}{}\text{(6)}& D_{\mathrm{dis}}=\frac{3a_{\mathrm{f}}{a}_{\mathrm{b}}}{2\sqrt{6}{a}_{\mathrm{b}}-3a_{\mathrm{f}}}\end{array}$$

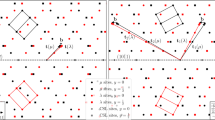
The example in Figure 6a is special, where s=0, a=|g_(110)b|/|g_(200)f|=0.8879 and $b=\left|\mathbf{g}(1\overline{1}\overline{2})\mathrm{b}|/|\mathbf{g}(0\overline{2}\overline{2})\mathrm{f}\right|=1.0875$. Substituting these values into Equations (3 and 4), one finds that θ=±5.7°, and the angle between n and the x axis is ±37.2°. The diffraction pattern after the rotation is shown Figure 6b, where the parallel Δg’s can be clearly seen, similar to the experimental result in Figure 2. Substituting the values of a_f and a_b into Equations (5 and 6) leads to ω=5.4° and D_dis≈1 nm. With the resultant OR and HP, the matching pattern in the HP can be plotted as shown in Figure 6c. In this figure, a set of dislocations is indicated between GMS clusters centred along O-lines. The dislocations are inclined with respected to the parallel Burgers vectors that lie horizontally in Figure 6c. The geometry of the dislocations is consistent with the analytical result. The atomic steps (structural ledges) are identified in Figure 6c, but they are better seen in the edge-on view of the HP along $\left[01\overline{1}\right]\mathrm{f}//\left[\overline{1}1\overline{1}\right]\mathrm{b}$ in Figure 6d. In this figure, one can also see that the related edge-on planes match edge-to-edge at the interface.

The O-line model can provide details of crystallographic information for an O-line interface as well as the configuration of the dislocation and ledge defect structure in the interface. This model has been successfully applied to interpret HPs in a number of fcc/bcc and hcp/bcc systems with various constraints to fix the remaining DOF.^37,59,60 Such constraints include the smallest deviation from a rational OR, the largest dislocation spacing and the requirement for the dislocation line to lie in a particular plane. The selection of constraints and the Burgers vector for the O-line interface are usually guided by experimental results. A geometric approach cannot usually predict which O-line interface will be observed. In principle, the thermodynamics and kinetics of the transformation should be taken into account for reliable predictions of the possible ORs and HPs. As a starting step towards this direction, the next section reviews some recent progress in the calculation of interfacial energies.

Interfacial energy, interfacial structure and morphology by atomistic simulations

As a result of rapid advances in computing techniques, atomistic simulations have become a powerful tool for obtaining fundamental knowledge of interfaces,⁹² and numerous results have been obtained both on the thermodynamics^{86,87,93–97} and the kinetics^98–103 of interfaces. However, the interfaces explored so far in kinetic simulations are not typical of those observed in experiments.^98–103 Therefore, we only concern ourselves here with calculations of interfacial energy by atomistic simulations. Before summarising the simulation results, several key issues that have substantial effects on the results, and that have not been paid sufficient attention in the past, will be discussed.

Selection of atomic potentials

To calculate the energy of a hetero-phase interface, the potentials of the adjacent phases should both be selected to avoid interface migration. When the interface tends to decompose into nanoscale facets and ledges, it is better to choose a potential that describes one element with two different stable crystal structures. Otherwise, the decomposition process will involve an energy barrier with transition of atoms from the stable structure to a metastable one in the region near the interface. The iron potential fitted by Yang and Johnson,⁹³ which assigns the fcc and bcc structure the same cohesive energy, is appropriate for an interfacial energy calculation in an fcc/bcc system. Results provided in this part are all calculated by employing this potential. Similarly, to study hcp/bcc systems, the potentials fitted by Oh and Johnson are good choices.¹⁰⁴

Construction of the initial atomic configuration

Special attention should be paid in constructing the initial atomic configurations of irrational interfaces. Geometric matching between the terrace–ledge–kink structures in an interface formed by joining two irrational surfaces is very complex. Some atoms may be too close, and others may be too far apart. These positions of large deviation from the normal atomic spacing are considered as interfacial interstitials and interfacial vacancies, respectively. They cannot be removed during a local relaxation, and these non-equilibrium interfacial defects will result in a significant overestimation of the interfacial energy.^86,96 Therefore, a proper initial atomic configuration, free of interfacial interstitials and vacancies is crucial for obtaining a reliable result for the interfacial energy. A simple method for constructing vacancy and interstitial free atomic configurations for a general interface has been proposed,⁹⁶ and this method is applied in the following cases.

Application to fcc/bcc systems

The HPs in fcc/bcc systems are typically in irrational orientations. To our knowledge, simulations of these complicated interfaces are still rare.^{86,87,93–97} The irrational HP in an fcc/bcc system is usually an O-line interface. Many O-line interfaces are possible corresponding to a related Burgers vector pair, as one DOF remains in the O-line condition. The possible Burgers vector pairs for an fcc/bcc system are of two types: ${\left[\overline{1}10\right]}_{\mathrm{f}}/2|{\left[\overline{1}00\right]}_{\mathrm{b}}$ and ${\left[01\overline{1}\right]}_{\mathrm{f}}/2|{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}/2$.⁸⁶ Corresponding to each Burgers vector pair, the variation of interfacial energy with the OR can be determined. Figure 7a shows the resultant energy curves, where the OR is specified by the angle, δ, between the related Burgers vectors. The shape of the energy curves can be qualitatively understood in terms of the dislocation structure, including the dislocation spacing and type,⁸⁶ which indicates the importance of energy contributions from misfit dislocations, especially the core structures. No unique minimum is identified for the ${\left[\overline{1}10\right]}_{\mathrm{f}}/2|{\left[\overline{1}00\right]}_{\mathrm{b}}$ O-line interfaces, whereas two minima are found for the ${\left[01\overline{1}\right]}_{\mathrm{f}}/2|{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}}/2$ O-line interfaces. One is a local minimum corresponding to δ≈−11.1°, and the other is the global minimum with δ≈0.5°, which is close to the K–S OR $({\left[01\overline{1}\right]}_{\mathrm{f}}//{\left[\overline{1}1\overline{1}\right]}_{\mathrm{b}},{\left(111\right)}_{\mathrm{f}}//{\left(011\right)}_{\mathrm{b}})$. A common feature of the two minima is that the dislocations lie on the nearly parallel planes (111)_f|(011)_b. Under these conditions, dislocation cores dissociate (or tend to dissociate) in the plane to Shockley partials, resulting in an energy reduction,⁸⁶ as shown in Figure 7b. The O-line interface associated with the lowest energy is in good agreement with the HPs of precipitates observed in Ni–Cr and Cu–Cr alloys,^46,57 confirming the relationship between energy singularity and the observation of faceted interfaces.

Figure 7

(a) Variation of interfacial energies of O-line interfaces with the OR for two types of Burgers vector pairs: $\left[\overline{1}10\left]\mathrm{f}/2|\right[\overline{1}00\right]\mathrm{b}$ and $\left[01\overline{1}\right]\mathrm{f}/2|\left[\overline{1}1\overline{1}\right]\mathrm{b}/2$. (b) Atomic structure of an $\left[01\overline{1}\left]\mathrm{f}/2|\right[\overline{1}1\overline{1}\right]\mathrm{b}/2$ O-line interface with δ≈−11.1°, showing dissociation of misfit dislocations into stacking faults. The viewing direction is $\left[\overline{1}01\right]\mathrm{f}|\left[\overline{1}\overline{1}1\right]\mathrm{b}$. Green, blue and red points are identified as positions with local fcc, bcc and hcp symmetries, respectively.

With the fixed OR for the O-line interface associated with the lowest energy, the energy variation of interfaces containing the IL has also been calculated. The results are plotted in Figure 8a, showing a correspondence between local energy minima with interfaces normal to principal Δg’s, which must be normal to the IL.³⁷ The energy values confirm quantitatively the association of principal Δg’s with singular interfaces, as shown by numerous experimental observations.¹⁵ On the basis of the energy data, the cross-section morphology was determined by the use of a Wulff construction (Figure 8b).⁹⁶ The calculated cross-section is consistent with experimental observations of lath-shaped precipitates^46,57 with two prominent preferred facets: the O-line interface and one normal to Δg_(020)f. Using the OR corresponding to the O-line interface observed in a duplex stainless steel, a similar calculation has been made to investigate the morphology of fcc precipitates.⁹⁷ The calculated rhombus cross-section (Figure 8d), is again consistent with the experimentally observed morphology.^97,105 This suggests that the cross-section morphology of precipitates is possibly governed by interfacial energy minimisation, even though small discrepancies exist between the calculated and observed morphologies. The atomic simulations of interfacial energy also yield data concerning the fine details of interfacial defect structures. Figure 8e shows the dissociation of coarsely spaced dislocations in the facet normal to $\Delta {\mathbf{g}}_{(\overline{1}11)\mathrm{f}}$ into stacking faults, which agrees well with experimental observations.¹⁰⁵ Figure 8f demonstrates the decomposition of the facet normal to Δg_(200)f into periodic nano-facets and ledges with each ledge associated with a [010]_f dislocation.

Figure 8

(a) Interfacial energies of interfaces that contain the IL direction with the OR determined by the lowest-energy O-line interface. (b) Equilibrium cross-section morphology determined by a Wulff construction using the energy data in a. c, d are similar to a, b with the O-line OR in a duplex stainless steel. φ represents the angle between the interface and the O-line interface (OLI). e, f represent interfacial structures of $\Delta {\mathbf{g}}_{(\overline{1}11)\mathrm{f}}$ and Δg_(200)f in c, respectively. Atoms are coloured by their structure, e.g., the green atoms locate at the cores of dislocations with a Burgers vector of ${\left[01\overline{1}\right]}_{\mathrm{f}}/2$.

Different potentials have also been employed to carry out similar calculations, e.g., the Cu–Fe potential fitted by Ackland et al.¹⁰⁶ was used in our previous calculations.^86,87,96 Irrespective of the differences between the energy values, it is notable that the overall shape of any energy curve is similar. Accordingly, from the point view of interfacial energy, the relative preference of interfaces in fcc/bcc systems with a_f/a_b~1.25 may not vary from alloy to alloy. Despite the similarity in the curve shape, the anisotropy of interfacial energy (i.e., the ratio between the maximum and minimum interfacial energies) is different, which results in the discrepancy between the relative areas of preferred facets. The similarities and discrepancies can be obtained by comparing Figure 8 with the results presented in previous work.⁹⁶ Although the above results are from the study of an fcc/bcc system, similar investigations can be carried out in other systems, e.g., hcp/bcc systems.

Summary

In this work, we have presented an integrated framework for describing all possible faceted interfaces. By assuming a correspondence between interfacial energy and structural singularities in a singular interface, structural singularity is considered to be the core feature of any singular interface. Three singular features, specified in a matching pattern, dislocation structure and/or ledge structure, may have a governing role, either independently or simultaneously. A singular interface governed by singularity in a ledge structure is normal to a low-index g defined in either lattice, and more often normal to two low-index g's from different lattices. When governed by singularity in a matching pattern, the interface is normal to Δg associated with two low-index g’s, and when governed by singularity in a dislocation structure, the interface is parallel to a POP, which must be normal to one or more selected Δg’s. In any case, a singular interface always has a discrete IO, convenient for one to distinguish it from its vicinal interfaces. A singular interface tends to be optimised with removal of the types of defects as far as possible. Such optimisation constrains the ORs, as can usually be described by one or more Δg’ parallelism rules, in combination with a selected constraint depending on the specific system. By the use of an integrated framework, the structure of various singular interfaces, as potential faceted interfaces, and their relationships with the constraints to the interface geometries are clearly demonstrated.

Almost all models for the interpretation of ORs and/or IOs rely on the principle of minimisation of interfacial energy, but the optimisation conditions or parameters used in the models differ. Various models can be grouped together depending on whether the model determines the OR, the IO for a given OR or the IO and OR together. The major results of most of these models can be incorporated in the integrated framework. Specific results have been discussed in various scenarios within this framework, corresponding to different singular features, and the links between the models are thus clarified. Minor discrepancies are discussed.

Irrational HPs in metallic systems have been the major concern of a number of models. Elimination of dislocations in one direction is possibly the governing singular feature. Hence, the misfit in the interface is fully compensated by a single set of dislocations, leading to an O-line interface. Analytical methods for the calculation of O-line interfaces are provided in both 2D and 3D situations. In the 2D analysis, the HP contains the Burger vector of the dislocations. Such a special irrational HP exhibits various structural features described by different models either exactly or approximately. In principle, the calculation methods for the primary preferred state can be applied to the interfaces in a secondary preferred state with minor modifications.

To further distinguish the relative preference of singular interfaces, atomistic simulations have been carried out using the interface geometries determined from geometric approaches as an input. The need for caution in constructing of the initial atomic configuration of an irrational interface is emphasised. If this is not carried out carefully, the calculated interfacial energy will be overestimated because of the presence of interfacial interstitials and vacancies. Application of atomistic simulations to fcc/bcc systems on one hand provides an in-depth understanding regarding the relative preference of singular interfaces, whereas on the other hand confirms the association between structural singularities and local energy minima, with the calculated equilibrium cross-sections in a good agreement with observations from selected alloys.