Abstract
Area laws were first discovered by Bekenstein and Hawking1,2, who found that the entropy of a black hole grows proportional to its surface area, and not its volume. Entropy area laws have since become a fundamental part of modern physics, from the holographic principle in quantum gravity3,4,5 to ground-state wavefunctions of quantum matter, where entanglement entropy is generically found to obey area law scaling6. As no experiments are currently capable of directly probing the entanglement area law in naturally occurring many-body systems, evidence of its existence is based on studies of simplified qualitative theories6,7,8. Using new exact microscopic numerical simulations of superfluid 4He, we demonstrate for the first time an area law scaling of entanglement entropy in a real quantum liquid in three dimensions. We validate the fundamental principle that the area law originates from correlations local to the entangling boundary, and present an entanglement equation of state showing how it depends on the density of the superfluid.
Similar content being viewed by others
Main
Condensed 4He undergoes a transition from a normal liquid to a superfluid phase at a critical temperature Tc ≃ 2.17 K, at its saturated vapour pressure9,10. Superfluid 4He was the first experimentally realized, and remains the most extensively studied, quantum phase of matter. Anomalous phenomena such as dissipationless flow, non-classical rotational inertia, quantized vortices and the Josephson effect have been thoroughly experimentally characterized11. Early theoretical work demonstrated the quantum mechanical origin of these phenomena12,13,14 where the Hamiltonian of liquid 4He is that of interacting spinless, non-relativistic bosons. Continuous space quantum Monte Carlo methods enable the precise computation of a wide range of its microscopic and thermodynamic properties, confirming theoretical predictions and reproducing experimental observations15. Moving beyond conventional simulations, recent algorithmic advances have opened up the possibility of measuring entanglement, the non-classical information shared between parts of a quantum state, in numerical experiments16,17. We combine these two technologies to measure the entanglement entropy in the superfluid phase of bulk 4He at zero temperature. Its ground state, | Ψ〉, in a cubic volume can be bipartitioned into a spherical subregion A and its complement  as shown in Fig. 1. The standard measure of entanglement between A and
as shown in Fig. 1. The standard measure of entanglement between A and  is the Rényi entropy, Sα(A) ≡ log(TrρAα)/(1 − α), where ρA is the reduced density matrix of the subsystem:
is the Rényi entropy, Sα(A) ≡ log(TrρAα)/(1 − α), where ρA is the reduced density matrix of the subsystem:  . The α = 1 case is most commonly known as the von Neumann entropy. The integer α ≥ 2 entropies have special physical significance, since they are related to the expectation value of an operator18. This allows for their evaluation using conventional measurement techniques, without resorting to full-state tomography. Since, from a many-body physics perspective, relevant features of entanglement (such as the area law) are quantifiable for any Rényi entropy, the natural choice, measured both in numerical simulations as well as recent experiments19, is α = 2. Here, we investigate its dependence on the radius R of the spherical subregion over a range of densities in the superfluid and find a dominant area law scaling: S2 ∼ R2.
. The α = 1 case is most commonly known as the von Neumann entropy. The integer α ≥ 2 entropies have special physical significance, since they are related to the expectation value of an operator18. This allows for their evaluation using conventional measurement techniques, without resorting to full-state tomography. Since, from a many-body physics perspective, relevant features of entanglement (such as the area law) are quantifiable for any Rényi entropy, the natural choice, measured both in numerical simulations as well as recent experiments19, is α = 2. Here, we investigate its dependence on the radius R of the spherical subregion over a range of densities in the superfluid and find a dominant area law scaling: S2 ∼ R2.
While there is no proof of the area law outside of a restrictive case in one spatial dimension20, it is the leading contribution to a scaling form that can be argued to arise from a few fundamental physical principles6,21,22,23,24. These are: S2(A) arises from correlations local to the entangling surface; and it has contributions at all length scales ℓ ranging from the microscopic scale of the interactions, r0, up to the characteristic size of the system, rf = min[R, ξ], where ξ is a correlation length. From these, a simple phenomenological scaling theory can be inferred for a spherical boundary of radius R in three dimensions (Fig. 1). For each infinitesimal region of the bounding surface dΣ, there is a local contribution to S2 from each length scale ℓ. For a given ℓ, the lowest order dimensionless quantity that can contribute to S2 is dΣ/ℓ2; when integrated over the surface this provides a contribution ∼R2/ℓ2. To account for contributions at all length scales, defined in the renormalization group sense, we integrate using a logarithmic measure23. This measure can be checked, for example, in the case of one dimension for a critical system with entangled region of size L, where it reproduces the appropriate scaling S2 ∼ log(L) (ref. 18). In three dimensions the resulting integral is : an area law. While higher order corrections lead to a power series in R, the symmetry of the entanglement entropy between complementary regions of pure states,  , limits this expansion to even powers (in odd dimensions). This leads to the generic scaling form,
, limits this expansion to even powers (in odd dimensions). This leads to the generic scaling form,

where a, b and c are dimensionless numbers. a is non-universal and depends on the microscopic details of the system, while b and c potentially encode universal information that is independent of the short-distance physics. Note that the leading-order area (as opposed to a volume) scaling and the absence of a subleading linear term are both features of the underlying physical principles in three dimensions.
We perform numerical tests of the general scaling form of equation (1) via high-performance simulations of superfluid 4He. Measuring S2 is significantly more computationally complex than for conventional estimators such as the energy and required the development of a new algorithm described in the Methods. The combined results of S2(R) for R ≤ L/2 are shown in Fig. 2 for the ground state of 4He at equilibrium density. We find that the entanglement entropy for different numbers of particles N collapses to a nearly universal curve. Before finite-size effects dominate near R ∼ L/2, and for R ≳ r0, we can fit the data to the scaling form in equation (1) with the dominant behaviour captured by a two-parameter fit (a, c) shown as a solid line. The extracted value of a is robust within ∼5% for fits including b ≠ 0 (details are provided in the Supplementary Information).
The ground state of N superfluid helium-4 atoms in a cubic cell with linear dimension L and periodic boundary conditions is bipartitioned into a sphere of radius R and its complement at fixed equilibrium density n0 = N/L3 ≃ 0.02186 Å−3. The Rényi entanglement entropy S2 in the limit R ≪ r0 is driven by particle fluctuations into the spherical subregion and is well described by free bosons (dotted line). For r0 ≲ R ≲ L/2 we perform the simplest fit of the numerical data to the leading-order behaviour of the scaling form in equation (1), using a two-parameter fit (a, c) with b = 0, shown as a solid line. Deviations from the universal curve for each system size occur as R approaches L/2, due to finite-size effects.
The efficacy of this fit and its confirmation of the leading-order scaling behaviour of the entanglement is investigated by computing the residuals between the simulation data and two scaling forms as shown in Fig. 3. We explore the area law predicted by equation (1), and a volume law that would be expected for an extensive entropy of thermodynamic origin. The residuals for the area law are consistent with zero, while strong deviations for the volume law exclude this as a candidate for the leading-order scaling. We observe no evidence of a subleading linear correction to the area law as predicted by equation (1). The systematic investigation of further subleading (non-constant) terms commensurate with equation (1) would require simulations of larger system sizes, providing a wider range of length scales.
The residuals of the Rényi entanglement entropy computed via quantum Monte Carlo (QMC) and two types of two-parameter fit corresponding to an area law: S2fit = 4πa(R/r0)2 + c and a volume law: S2fit = (4πa/3)(R/r0)3 + c for N = 64 4He atoms at the equilibrium density n0. Residuals are shown for values of the spherical subregion radius R over which the fits were performed. The data are poorly described by the volume law and support the area law scaling predicted in equation (1).
To understand the physical origin of the area law scaling coefficient a, we define an entanglement length scale  . From a fit to equation (1), ℓe ≃ 1.3r0 ≍ 5 Å at n = n0. This strongly suggests that the short-distance physics of the potential hard core and adjacent attractive minima dominate the area law scaling behaviour.
. From a fit to equation (1), ℓe ≃ 1.3r0 ≍ 5 Å at n = n0. This strongly suggests that the short-distance physics of the potential hard core and adjacent attractive minima dominate the area law scaling behaviour.
To confirm, we study the effect of the density on the entanglement by computing S2 for superfluid 4He over a range of densities near n0 corresponding to positive (n > n0) and negative (n < n0) pressures. Performing a two-parameter fit to the area law scaling for each density, we plot an ‘entanglement equation of state’ in Fig. 4. a is an increasing function of density, and thus a monotonic function of pressure (see inset). We find that ℓe depends both on the nature of short-distance interaction as well as the interparticle separation. We can contrast this behaviour to the non-interacting Bose gas, where S2(R) is a pure function of the aspect ratio R/L.
The area law coefficient a versus density n in the ground state of 4He in the superfluid regime, as computed by two-parameter fits to quantum Monte Carlo data for N = 64 (symbols); the line is a guide for the eye. Inset: the pressure P of the ground state of superfluid 4He as a function of density, from ref. 30. This suggests that a is a monotonic function of pressure. The dashed vertical lines correspond to the equilibrium density n0 ≃ 0.02186 Å−3.
In conclusion, we have demonstrated that the prototypical quantum fluid, superfluid 4He, displays area law scaling of its entanglement entropy. Using large-scale, exact microscopic simulations, we have extracted the numerical coefficient of the area law term and find that it is a monotonically increasing function of density. This confirms that fluctuations and interactions local to the entangling boundary drive the physics of the area law. These fluctuations also play an important role in constraining the subleading scaling of the entanglement entropy, which contains new universal physics. For example, it is predicted that logarithmic corrections should arise due to the existence of a spontaneously broken continuous symmetry in the thermodynamic limit, contributing a universal coefficient due to the presence of a low-energy ‘tower of states’ spectrum and a Goldstone boson25,26,27. For superfluid 4He with a spherical entangling surface, this b coefficient will combine with another universal number arising from the vacuum theory governing the bosonic fluctuations. This latter quantity encodes one of the two central charges that characterize a three-dimensional conformal field theory28, believed to be the fundamental constant that quantifies how entropymonotonically decreases under renormalization group flow29. A curved bounding surface such as a sphere without defects is only possible in the spatial continuum. It is thus possible that fundamental physical quantities that arise for smooth geometries are inaccessible in simple lattice models and can be probed only in Galilean-invariant quantum liquids.
Methods
The Hamiltonian of bulk liquid 4He is that of spinless, non-relativistic bosons interacting with a two-body interatomic potential:

where ℏ2 is the reduced Planck’s constant and m is the mass. Accurate microscopic interatomic potentials V for 4He have been developed31 that include a repulsive hard core of radius σ ≃ 2.6 Å, an attractive power-law tail, and a minimum of depth ε ≃ 11 K at radius rm ≃ 3.0 Å. At the equilibrium number density n0 ≃ 0.02186 Å−3, the mean interparticle separation r0 ≃ 3.6 Å is slightly larger than rm. The use of V in conjunction with path integral quantum Monte Carlo methods has allowed for precise calculations of a wide range of ground state and finite temperature properties of liquid helium15 for N of order 104 atoms32.
In recent work we have extended these Monte Carlo methods to compute Rényi entropies in systems of itinerant particles in the spatial continuum16,17,33,34. Due to the increased computational difficulty of computing Rényi entropies, the data presented here are limited to N ≤ 64 4He atoms. However, systems of this size have been demonstrated to be sufficiently large to display fundamental macroscopic features of superfluid 4He (ref. 15).
While our previously published algorithm was focused on one spatial dimension, for this work we have developed a new variant that allows for the computation of Rényi entropies in the ground state of systems of interacting bosons in three-dimensional continuous space. We use a path integral method15,35 that gives access to group state properties via imaginary-time projection on a trial state |ΨT〉:

We label the classical configuration space of N bosons by R, which is a vector of three-dimensional particle coordinates. Considering Hamiltonians of the form equation (2), we use a standard approximation to the imaginary-time propagator

which is accurate to fourth order in the short time τ (refs 36,37). Because equation (4) is non-negative for bosonic systems, we can Monte Carlo sample discrete imaginary-time world-line configurations, where we use P discrete time steps with 2β = Pτ.
For the second Rényi entropy, we define a replicated Hilbert space of two non-interacting copies of the system,  . We may compute S2 under a bipartition of the system into A and its complement
. We may compute S2 under a bipartition of the system into A and its complement  from the expectation value of a ‘swap operator’ that swaps the configuration of A between the two replicas:
from the expectation value of a ‘swap operator’ that swaps the configuration of A between the two replicas:

where  such that RA (
such that RA ( ) is a vector of the coordinates of the particles in A (
) is a vector of the coordinates of the particles in A ( ). The estimator for S2 is then simply related to the expectation value of the swap operator16:
). The estimator for S2 is then simply related to the expectation value of the swap operator16:

To compute equation (5) with path-integral ground-state Monte Carlo, we use equation (3), and consider imaginary-time paths of length 2β, capped by ΨT on either end of the path. We Monte Carlo sample an extended configuration space of imaginary-time world lines that includes configurations where world lines that pass through A at imaginary time β may swap between replicas. That is, world lines that pass through the  spatial subregion at time β are always propagated in imaginary time along the same replica, but particles that pass through the A subsystem at time β may be connected via ρτ to a world line in
spatial subregion at time β are always propagated in imaginary time along the same replica, but particles that pass through the A subsystem at time β may be connected via ρτ to a world line in  or RA at time β + τ. Such swapped world-line configurations have weight of the form
or RA at time β + τ. Such swapped world-line configurations have weight of the form

where ρτA ( ) are the reduced propagators for the A (
) are the reduced propagators for the A ( ) subsystem17,34 and Rj is the configuration of N particles at imaginary time jτ. By including updates that allow for the world-line connectivity to interchange between swapped (s) and unswapped (u) configurations, we may measure S2 from equation (5) from the ratio of the swapped and unswapped generalized partition functions:
) subsystem17,34 and Rj is the configuration of N particles at imaginary time jτ. By including updates that allow for the world-line connectivity to interchange between swapped (s) and unswapped (u) configurations, we may measure S2 from equation (5) from the ratio of the swapped and unswapped generalized partition functions:

We find this estimator to be more efficient than previous variants for systems above one spatial dimension. To further improve its performance we used a ‘ratio method’ to build up A from smaller increments33,38. The systematic errors due to finite τ and β can be made arbitrarily small by increasing P at a computational cost that is polynomial in P and N with details shown in the Supplementary Information. All results shown were computed using β = 0.48 K−1, τ = 0.005 K−1, and a constant trial wavefunction.
Data availability.
All quantum Monte Carlo data that were used to generate the plots within this paper and other findings of this study are available from the corresponding author on reasonable request.
Additional Information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bekenstein, J. D. Black holes and entropy. Phys. Rev. D 7, 2333–2346 (1973).
Hawking, S. W. Black hole explosions? Nature 248, 30–31 (1974).
’t Hooft, G. On the quantum structure of a black hole. Nucl. Phys. B 256, 727–745 (1985).
Susskind, L. The world as a hologram. J. Math. Phys. 36, 6377–6396 (1995).
Bousso, R. The holographic principle. Rev. Mod. Phys. 74, 825–874 (2002).
Eisert, J., Cramer, M. & Plenio, M. B. Colloquium: area laws for the entanglement entropy. Rev. Mod. Phys. 82, 277–306 (2010).
Bombelli, L., Koul, R. K., Lee, J. & Sorkin, R. D. Quantum source of entropy for black holes. Phys. Rev. D 34, 373–383 (1986).
Srednicki, M. Entropy and area. Phys. Rev. Lett. 71, 666–669 (1993).
Allen, J. F. & Misner, A. D. Flow phenomena in liquid helium II. Nature 142, 643–644 (1938).
Kapitza, P. Viscosity of liquid helium below the λ-point. Nature 141, 74 (1938).
Leggett, A. Quantum Liquids: Bose Condensation and Cooper Pairing in Condensed-Matter Systems (Oxford Univ. Press, 2006).
London, F. The λ-phenomenon of liquid helium and the Bose–Einstein degeneracy. Nature 141, 643–644 (1938).
Tisza, L. Transport phenomena in helium II. Nature 141, 913 (1938).
Landau, L. Theory of the superfluidity of helium II. Phys. Rev. 60, 356–358 (1941).
Ceperley, D. M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 67, 279–355 (1995).
Hastings, M. B., González, I., Kallin, A. B. & Melko, R. G. Measuring Renyi entanglement entropy in quantum Monte Carlo simulations. Phys. Rev. Lett. 104, 157201 (2010).
Herdman, C. M., Roy, P.-N., Melko, R. G. & Del Maestro, A. Particle entanglement in continuum many-body systems via quantum Monte Carlo. Phys. Rev. B 89, 140501 (2014).
Calabrese, P. & Cardy, J. Entanglement entropy and quantum field theory. J. Stat. Mech. Theor. Exp. 2004, P06002 (2004).
Islam, R. et al. Measuring entanglement entropy in a quantum many-body system. Nature 528, 77–83 (2015).
Hastings, M. B. An area law for one-dimensional quantum systems. J. Stat. Mech. Theor. Exp. 2007, P08024 (2007).
Liu, H. & Mezei, M. A refinement of entanglement entropy and the number of degrees of freedom. J. High Energy Phys. 2013, 162–206 (2013).
Solodukhin, S. N. Entanglement entropy of round spheres. Phys. Lett. B 693, 605–608 (2010).
Swingle, B. Mutual information and the structure of entanglement in quantum field theory. Preprint at https://arxiv.org/abs/1010.4038 (2010).
Grover, T., Turner, A. M. & Vishwanath, A. Entanglement entropy of gapped phases and topological order in three dimensions. Phys. Rev. B 84, 195120 (2011).
Song, H. F., Laflorencie, N., Rachel, S. & Le Hur, K. Entanglement entropy of the two-dimensional Heisenberg antiferromagnet. Phys. Rev. B 83, 224410 (2011).
Kallin, A. B., Hastings, M. B., Melko, R. G. & Singh, R. R. P. Anomalies in the entanglement properties of the square-lattice Heisenberg model. Phys. Rev. B 84, 165134 (2011).
Metlitski, M. A. & Grover, T. Entanglement entropy of systems with spontaneously broken continuous symmetry. Preprint at http://arxiv.org/abs/1112.5166 (2011).
Casini, H. & Huerta, M. Entanglement entropy for the n-sphere. Phys. Lett. B 694, 167–171 (2010).
Cardy, J. L. Is there a c-theorem in four dimensions? Phys. Lett. B 215, 749–752 (1988).
Maris, H. J. & Edwards, D. O. Thermodynamic properties of superfluid 4He at negative pressure. J. Low Temp. Phys. 129, 1–24 (2002).
Aziz, R. A., Nain, V. P. S., Carley, J. S., Taylor, W. L. & McConville, G. T. An accurate intermolecular potential for helium. J. Chem. Phys. 70, 4330–4342 (1979).
Boninsegni, M., Prokof’ev, N. & Svistunov, B. Worm algorithm for continuous-space path integral Monte Carlo simulations. Phys. Rev. Lett. 96, 070601 (2006).
Melko, R. G., Kallin, A. B. & Hastings, M. B. Finite-size scaling of mutual information in Monte Carlo simulations: application to the spin-1/2 XXZ model. Phys. Rev. B 82, 100409 (2010).
Herdman, C. M., Inglis, S., Roy, P.-N., Melko, R. G. & Del Maestro, A. Path-integral Monte Carlo method for Rényi entanglement entropies. Phys. Rev. E 90, 013308 (2014).
Sarsa, A., Schmidt, K. E. & Magro, W. R. A path integral ground state method. J. Chem. Phys. 113, 1366–1371 (2000).
Chin, S. A. Symplectic integrators from composite operator factorizations. Phys. Lett. A 226, 344–348 (1997).
Jang, S., Jang, S. & Voth, G. A. Applications of higher order composite factorization schemes in imaginary time path integral simulations. J. Chem. Phys. 115, 7832–7842 (2001).
Herdman, C. M., Roy, P.-N., Melko, R. G. & Del Maestro, A. Spatial entanglement entropy in the ground state of the Lieb-Liniger model. Phys. Rev. B 94, 064524 (2016).
Acknowledgements
We are grateful to L. H. Sierens and M. Metlitski for useful discussion. This research was supported in part by the National Science Foundation under Awards No. DMR-1553991 (A.D.) and PHY-1125915 (R.G.M.). Additionally, we acknowledge support from the Natural Sciences and Engineering Research Council of Canada, the Canada Research Chair programme, the Canada Foundation for Innovation, and the Perimeter Institute for Theoretical Physics. Computations were performed on the Vermont Advanced Computing Core supported by NASA (NNX-08AO96G) as well as on resources provided by the Shared Hierarchical Academic Research Computing Network (SHARCNET). Research at Perimeter Institute is supported through Industry Canada and by the Province of Ontario through the Ministry of Research and Innovation.
Author information
Authors and Affiliations
Contributions
The quantum Monte Carlo code was written by A.D. and C.M.H. with C.M.H. running all numerical simulations and performing the data analysis. All authors contributed to the interpretation of results and the writing of the manuscript and Supplementary Information.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 271 kb)
Rights and permissions
About this article
Cite this article
Herdman, C., Roy, PN., Melko, R. et al. Entanglement area law in superfluid 4He. Nature Phys 13, 556–558 (2017). https://doi.org/10.1038/nphys4075
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys4075
This article is cited by
-
Measuring entanglement entropy and its topological signature for phononic systems
Nature Communications (2024)


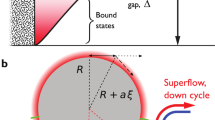

 at fixed density n ≡ 1/r03. The entanglement between A and
at fixed density n ≡ 1/r03. The entanglement between A and  is dominated by an area law, scaling with area of the bounding surface.
is dominated by an area law, scaling with area of the bounding surface.

