Intertwined superfluid and density wave order in two-dimensional ⁴He

Abstract

Superfluidity is a manifestation of the operation of the laws of quantum mechanics on a macroscopic scale. The conditions under which superfluidity becomes manifest have been extensively explored experimentally in both quantum liquids (liquid ⁴He being the canonical example) and ultracold atomic gases^1,2, including as a function of dimensionality^3,4. Of particular interest is the hitherto unresolved question of whether a solid can be superfluid^5,6. Here we report the identification of a new state of quantum matter with intertwined superfluid and density wave order in a system of two-dimensional bosons subject to a triangular lattice potential. Using a torsional oscillator we have measured the superfluid response of the second atomic layer of ⁴He adsorbed on the surface of graphite, over a wide temperature range down to 2 mK. Superfluidity is observed over a narrow range of film densities, emerging suddenly and subsequently collapsing towards a quantum critical point. The unusual temperature dependence of the superfluid density in the limit of zero temperature and the absence of a clear superfluid onset temperature are explained, self-consistently, by an ansatz for the excitation spectrum, reflecting density wave order, and a quasi-condensate wavefunction breaking both gauge and translational symmetry.

Main

Superfluid ⁴He is described by a condensate wavefunction ψ(r) = ψ₀e^iϕ(r), with long-range coherence of the global phase ϕ(r), determining the quantum hydrodynamic and non-classical rotation properties^1,2. In two dimensions the superfluid state has power-law correlations of the local phase^4,7,8. Whereas in bulk the destruction of superfluidity at finite transition temperature arises from the creation of thermal excitations (phonons and rotons), in two dimensions topological excitations (vortices) play a crucial role. In this case the quasi-condensate is suddenly destroyed at the Berezinskii–Kosterlitz–Thouless (BKT) phase transition by the unbinding of vortex–antivortex pairs, accompanied by a universal jump in superfluid density^3,7. On the other hand, superfluidity may be destroyed at a T = 0 quantum phase transition by increasing correlations or disorder. Here the classic example is the superfluid–Mott insulator transition⁹, which has been observed in cold bosonic atoms in optical lattices^10,11, by tuning the periodic potential.

The novelty of the putative supersolid is that it manifests both superfluid and density wave order¹². Unambiguous detection has proved elusive in bulk solid ⁴He (refs 6,13), where a variety of scenarios have been proposed to establish superfluidity coexisting with solid order. These involve mobile zero-point vacancies, frozen-in dislocations and disorder^14,15, and the defects determine the strength of the superfluid response. Supersolids have been predicted on model two-dimensional (2D) quantum lattices, again arising from mobile vacancies and favoured by triangular lattice symmetry¹⁶. Several schemes to realize supersolids in ultracold atoms have also been proposed^17,18. By contrast, in this work we report evidence for a uniform quantum state, in which solidity and superfluidity are quantum-entangled.

Our experiment exploits helium on graphite as a model system to study the interplay of superfluidity with film structure on increasing the film coverage (number of atoms per nm²)¹⁹. Since the surface of graphite is atomically flat, the film grows with the addition of ⁴He atoms through the progressive formation of distinct atomic layers. The completed first layer forms a triangular close-packed structure, incommensurate with the graphite surface potential (Fig. 1b). Here we report on the superfluid response of the second layer, which comprises a 2D system of strongly correlated bosons, of tunable density, subject to the periodic lattice potential arising from the first layer solid. On growing the second layer it first forms a gas–liquid coexistence, with 2D liquid puddles at the self-bound density of around 4.5 nm⁻², then a uniform 2D liquid^20,21,22. Close to layer completion, these theoretical simulations agree that the second layer forms a 2D solid, incommensurate with the first layer. At somewhat lower coverages, measurements of a series of heat capacity peaks^23,24 provide possible signatures of the melting of density wave order. However, in this regime, the results of simulations on the stability of a solid phase depend on details of the treatment of the helium–graphite potential and the quantum zero-point motion of first-layer atoms^21,22,25 (see also Supplementary Information).

Figure 1: Frequency shifts of torsional oscillator.

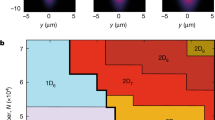
a, Double torsional oscillator, cut away to show graphite substrate, on which helium film is physisorbed. b, Two-layer ⁴He film. The first layer of ⁴He (pink spheres) on graphite forms a 2D close-packed triangular lattice. Second layer (blue) is shown as a solid on a triangular lattice. c, Frequency shift of torsional oscillator at a series of helium film coverages, following subtraction of empty cell background. The frequency shift due to full mass loading of the normal film, determined at 1.5 K, has been subtracted from the frequency shift data (Supplementary Information). The frequency shift due to superfluidity appears after 17.11 nm⁻², reaching a maximum at 18.09 nm⁻², and disappears at 19.96 nm⁻² (these three bounds are highlighted). Data from 17.25 to 18.01 nm⁻² are not shown for clarity, see Supplementary Information. The monotonic evolution of the frequency shift as a function of coverage in the temperature range 0.1 to 1 K arises from the coverage dependence of the viscoelastic response of the substrate/film composite system. d, Dissipation of torsional oscillator at the same helium film coverages, following subtraction of empty cell background. The dissipation shows a systematic evolution, correlated with film structure (Supplementary Information). At the lowest temperatures the dissipation is smaller than that of the empty cell. e, Illustration of composite background subtraction for data set at 19.02 nm⁻². The superfluid response (red line) is inferred by first subtracting the viscoelastic response of a non-superfluid reference sample 17.1 nm⁻² (result shown as black line). A correction to take into account coverage dependence of viscoelastic response is made by a fit (blue line) to this data (black line) over the temperature interval shown, highlighted in grey. Subtracting this background correction results in the superfluid response (red line). See Supplementary Information for further details. f, Isotherm of frequency shift, after composite background subtraction, at 2.5 mK. The error bars reflect uncertainties in the subtraction of frequency shift due to mass loading or the background subtraction, whichever is greater. The vertical dashed lines (blue) indicate, for reference purposes, triangular superlattices (Supplementary Information), with densities relative to first layer of 4/7, 7/12. Coverage at which promotion to the third layer occurs is shown by vertical dashed red line.

We use a torsion pendulum (Fig. 1a) as a probe of the superfluid density, a quantity not directly accessed hitherto in cold-atom systems²⁶. This technique was first used in superfluid ⁴He by Andronikashvili²⁷, and has been extensively refined to study superfluid quantum liquids in bulk and two dimensions. In the two-fluid model of superfluidity, the superfluid density at finite temperature is given by ρ_s(T) = ρ_s(0) − ρ_n(T), where ρ_s(0) = ρ, the total fluid density, in the case of bulk superfluid ⁴He. The superfluid component decouples from the motion of the oscillator, giving rise to an increase in resonance frequency (Fig. 1c). As first shown by Landau for superfluid ⁴He bulk liquid, the normal density ρ_n(T) may be calculated from the bosonic elementary excitation spectrum²⁸. Measurement of this quantity, by this technique, therefore constitutes a thermodynamic determination of the excitation spectrum. The analysis is independent of assumptions about the quantum condensate, yet provides essential insights into the nature of that condensate.

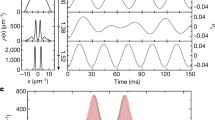
The frequency shift due to superfluidity, as a function of coverage, is determined after composite background subtraction, illustrated in Fig. 1e (Supplementary Information). Our experiments extend to ultralow temperatures, which is essential to establish the zero-temperature limit of the superfluid density. A frequency shift isotherm, at the lowest temperature (Fig. 1f), shows that superfluidity occurs over a narrow range of coverage in the second layer. The temperature dependence of the frequency shift (Fig. 2a) is unusual in several respects. There is no clear superfluid onset temperature, or a jump in superfluid density at a finite temperature, as expected in a 2D superfluid with broken U(1) gauge symmetry; rather a gradual increase in superfluid density. With increasing coverage both the T = 0 frequency shift, reflecting ρ_s(0), and the characteristic temperature, which governs the gradual appearance of superfluid response on cooling, decrease. Our results are consistent with earlier measurements¹⁹, taken at a limited number of coverages to a minimum temperature of 20 mK.

Figure 2: Scaling of superfluid density.

a, Temperature dependence of superfluid frequency shift for coverages 18.09 to 19.57 nm⁻² (second-layer density 6.32 to 7.69 nm⁻²), following composite background subtraction. The inset re-plots the isotherm of Fig. 1f, to show coverage ranges of scaling collapse: regions I (blue points) and II (red points) show single-parameter scaling (see main text and Supplementary Information); regions A and B (green points) show two-parameter scaling. Also shown are phase boundaries identified in ref. 24 (blue dashed lines), from coverage dependence of heat capacity maxima (with coverages scaled by 0.943 (Supplementary Information)) and third layer promotion (red dashed line), which are in good agreement with the boundaries of the different scaling regimes. b, Scaled superfluid density showing collapse over two coverage regimes achieved by single-parameter scaling. I: 18.09 to 18.41 nm⁻² (five studied coverages). II: 18.50 to 19.24 nm⁻² (nine studied coverages). c, Coverage dependence of characteristic energy scale, Δ, inferred from the single-parameter scaling procedure in regions I and II. Vertical dashed line shows promotion to third layer. The density dependence of Δ determines, by extrapolation, a quantum critical point at a total coverage 19.9 ± 0.05 nm⁻², at which simulations^21,22 predict the second layer to form a localized close-packed solid. Over this coverage range the first layer density increases from 11.8 to 11.9 nm⁻². Dashed lines are guides to the eye. Two-parameter scaling behaviour in region B is discussed in Supplementary Information.

We calibrate the magnitude of the superfluid density using the BKT transition of a thicker ⁴He film consisting of a fluid layer atop two solid layers (Supplementary Information). This allows us to convert the frequency shift data measured in the second layer to superfluid fraction ρ_s(T)/ρ. This calibration shows that the maximum superfluid response at 18.09 nm⁻² corresponds to ρ_s(0)/ρ ∼ 0.8, and demonstrates that it is a property of essentially the entire layer.

The temperature dependence of the superfluid fraction at different coverages exhibits a remarkable scaling behaviour (Fig. 2b). We introduce the parameter Δ(n), as a coverage-dependent characteristic temperature. We find that the data divide into four coverage regimes (Fig. 2a, inset). Of particular interest are regions I (18.09 to 18.41 nm ⁻²) and II (18.50 to 19.24 nm⁻²), where the data can be collapsed using a single-parameter scaling according to the form (ρ_s(T, n)/ρ) = (Δ(n)/T₀)f(T/Δ(n)). The scaling procedure (Supplementary Information) requires no assumption about the functional form. Δ(n) is the only adjustable parameter, which determines the T = 0 superfluid density, ρ_s(0, n) = ρ(Δ(n)/T₀), and is the characteristic temperature controlling superfluid onset. The normalization factor T₀ is chosen so that f(0) = 1. Figure 2b shows that different functions apply to regimes I and II.

It is striking that scaling extends over the full temperature range in both these regimes. They show distinct behaviour in the magnitude and coverage dependence of Δ (Fig. 2c), which provides evidence of the interplay between superfluidity and film structure, with a distinct transition in film structure around 18.45 nm⁻². In regime II the temperature dependence of the superfluid density is well described by f(T/Δ) = (1 + T/Δ)⁻¹, up to T/Δ ∼ 4. A fit of the collapsed data to this form is used to determine the absolute values of Δ, shown in Fig. 2c, and the parameter T₀.

For regime II, we find Δ(n) ∝ δ, with coverage as the tuning parameter δ = n_c − n providing compelling evidence for quantum criticality (Fig. 2c). The collapse of the energy scale Δ(n) and ρ_s(0) at coverage n_c = 19.9 nm⁻², by extrapolation, identifies this as the quantum critical point (QCP). The approach to the QCP is interrupted by a coverage range (labelled B in Fig. 2a, inset) where single-parameter scaling breaks down; in this region the characteristic temperature governing superfluid onset continues to collapse towards the QCP. The scaling of regime II is consistent with a superfluid–insulator transition in the Bose–Hubbard universality class⁹.

These results show that the leading-order temperature dependence of the superfluid density is ρ_s(T, n)/ρ = ρ_s(0, n)/ρ − T/T₀, where ρ_s(0, n)/ρ = Δ(n)/T₀. This linear decrease in superfluid density with increasing temperature, observed in the T → 0 limit, is much faster than the T³ dependence expected for 2D phonon-like excitations.

The famous Landau formula, deriving the normal density ρ_n(T), is a momentum-weighted thermal average over the bosonic elementary excitation spectrum²⁸. We propose the elementary excitation spectrum, shown in Fig. 3a, to account for the observed leading-order linear in T behaviour of ρ_n(T). The high density of states of softening roton-like modes at finite momentum, around the six density wave ordering wavevectors of a triangular lattice G_i, gives the dominant contribution to the normal density as ρ_nδ_ij = −∑_GG_iG_j∫ (d²p/(2πℏ)²)(∂/∂E_p)(1/(exp(E_p/k_BT) − 1). For an assumed incommensurate second-layer triangular structure the density is and the normal fraction is , when E₀ < k_BT, which agrees with the observed leading-order temperature dependence, within the logarithmic correction (Supplementary Information), and implies an upper bound on E₀/k_B of order 1 mK. In regime II, fits to the collapsed data determine T₀ = 21 mK. Hence the characteristic speed c ∼ 50 ms ⁻¹.

Figure 3: Ansatz for elementary excitation spectrum and condensate wavefunction.

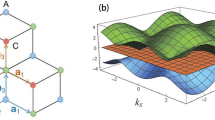
a, Ansatz for the dispersion relation of elementary excitations in the anomalous superfluid ⁴He monolayer. We take the form (blue line), where c is a characteristic speed and E₀ is an effective roton-like gap. b, There are six softening roton-like modes at the density wave ordering wavevectors , where corresponds to a triangular lattice of side length a. c, Simplified illustration of condensate |Ψ〉 = [cos(θ/2) |0〉 + e^iϕ sin(θ/2) |G〉]e^iχ with SU(2) symmetry, with condensation into states of momentum 0, G. The amplitude of the density modulation varies as sinθ. For more details and generalization see Supplementary Information. This symmetry implies that vortices are not stable, and explains the absence of a BKT transition.

This form of excitation spectrum is a natural consequence of incipient density wave ordering. For a superfluid, the form of the dispersion relation is qualitatively related to the structure factor S(k) through Feynman’s expression E(k) = ℏ²k²/2mS(k)²⁹. The S(k) inferred from our ansatz for the dispersion has sharp maxima at G_i, reflecting density wave order. Our measurements of the superfluid density demonstrate both superfluid and density wave order, with no a priori assumption about the structure of the second layer.

Furthermore, and consistent with the ansatz for the excitation spectrum, we propose an ansatz for a coherent ground state, with a quasi-condensate at both zero momentum and at the discrete set of finite momenta G_i, |Ψ〉 = exp(α₀b_q=0^† + ∑_Gα_Gb_G^†) |0〉 (Supplementary Information). This state simultaneously breaks both gauge symmetry (superfluidity) and translational symmetry (density wave order). Given the density operator, , density wave order necessarily implies a condensate at G, in the presence of a superfluid condensate. The existence of essentially gapless modes at G_i, as in the proposed excitation spectrum, implies a larger manifold of degenerate states (Fig. 3c). This is an unconventional non-Abelian superfluid. According to homotopy theory, vortices are no longer stable, explaining the observed absence of a BKT transition. This coherent state is distinct from a fragmented condensate, where separate sets of atoms condense into different single-particle states³⁰.

Studies of the nuclear magnetism in the fermionic ³He cousin of this system, at the same second-layer coverages, clearly demonstrate a Mott insulator local moment phase, with strong exchange interactions arising from particle permutations, leading to a proposed quantum spin liquid ground state³¹. The present experiment explores the consequences of the highly quantum nature of the system in the bosonic case. Our results provide direct evidence, through the measurement of superfluid mass decoupling, for a new superfluid state of matter, which is tunable and exhibits scaling collapse. Intertwined density wave and superfluid order profoundly alters the symmetry of the quasi-condensate and its response. Anderson’s contention is that “every pure Bose solid’s ground state is a supersolid”¹⁵. The condition of extreme quantum motion realized in this 2D helium system makes it observable at accessible temperatures. Our scenario demonstrates how density wave order and superfluidity can coexist, contributing towards the resolution of the supersolid enigma. Direct measure of the structure factor (in regimes A, I, II, B), and of phase coherence would be of great interest.

Methods

The torsional oscillator contains an exfoliated graphite substrate (Supplementary Information) onto which a helium film is adsorbed. It has a resonance frequency of 1,423 Hz; motion is driven and detected capacitatively. The resonance frequency and quality factor are determined from the quadrature and in-phase response to a constant drive, maintaining the drive frequency within 5 μHz of resonance. The substrate consists of 48 sheets of exfoliated graphite, diffusion bonded to silver foils, which are in turn diffusion bonded to the torsional oscillator for effective thermalization at ultralow temperatures. To perform measurements over a wide temperature range, from 4 K to below 2 mK, the torsional oscillator is mounted on a copper plate, cooled by a nuclear demagnetization stage through a weak thermal link. Thermometry, also mounted on the copper plate, is provided by a carbon glass thermometer (above 1.3 K), germanium thermometer (50 mK to 6 K, calibrated by the manufacturer) and a ³He melting curve thermometer (1 mK to 250 mK, self-calibrated using the superfluid A transition as a fixed point). This arrangement allows the temperature to be conveniently swept, at the expense of minimum temperature, which is 1.2 mK.

The frequency shift and dissipation of the empty oscillator are first measured. Helium is adsorbed onto the substrate by dosing from a calibrated standard volume which forms part of a room-temperature gas handling system. To convert from STPcm³ to film density we perform a vapour pressure isotherm at 4.2 K. For our sample, point-B corresponds to 15.23 cm³, following a dead volume correction. We define our coverage scale by setting this fiducial point at 11.4 nm⁻². The mass loading of the oscillator measured at 1.5 K is −9.33 mHz STPcm⁻³. The empty cell background-subtracted frequency and dissipation as a function of temperature have a smooth and systematic evolution with film coverage. The superfluid mass decoupling appears, then disappears over a narrow range of second-layer film densities, accompanied by a monotonic evolution of the frequency shift, most pronounced at higher temperatures, which is attributed to the viscoelastic response of the substrate–adsorbate composite. This behaviour allows us to generate a composite background for the frequency shift data in order extract the superfluid response. Estimates of the systematic errors in composite background subtraction, the bound on the superfluid critical velocity, and issues around substrate morphology are discussed in accompanying Supplementary Information.

Data availability.

The data that support the plots within this paper and other findings of this study are available from the corresponding author on reasonable request, and also from https://dx.doi.org/10.6084/m9.figshare.4290752.