Main

For quantum dots accommodating an odd number of electrons, a suppression of charge fluctuations in the Coulomb-blockade regime leads to a local spin-1/2 degree of freedom and, when temperature is lowered through a characteristic Kondo temperature TK, the Kondo effect shows up as a zero-bias peak in the differential conductance. In a dot with an even number of electrons, the two electrons residing in the highest occupied level may either form a singlet or promote one electron to the next level to form a triplet, depending on the relative magnitude of the level splitting δ and the ferromagnetic intradot exchange energy J. For J>δ, the triplet state prevails and gives rise to a zero-bias Kondo peak7,8, but when δ>J the singlet state is lower in energy and no Kondo effect is expected in the linear conductance. Nevertheless, spin-flip tunnelling becomes viable when the applied bias is large enough to induce transitions from singlet to triplet states. Such interlead exchange–tunnelling may give rise to Kondo correlations and concomitant conductance peaks near V ∼±δ/e, where e is the elementary charge. However, because the tunnelling involves excited states with a rather limited lifetime, the extent to which the coherence of such inelastic spin flips, and hence the extent to which the Kondo effect is maintained, remains unanswered.

The possibility of finite-bias conductance anomalies induced by the Kondo effect was discussed in 1966 by Appelbaum16, and a detailed account of the subsequent development of this problem can be found in ref. 17. In the context of a double-dot system, a qualitative description of a finite-bias Kondo-effect, treating decoherence and non-equilibrium effects in an incomplete way, is given in ref. 18. Finite-bias conductance peaks have already been observed in carbon nanotubes11,14,19 as well as in GaAs quantum dots8,9,20. However, owing to the lack of a quantitative theory for this non-equilibrium resonance, characterization of the phenomenon has not yet been possible. As pointed out in refs 17, 21, 22 a bias-induced population of the excited state (here the triplet), may change a simple finite-bias cotunnelling step into a cusp in the nonlinear conductance. Therefore, to quantify the strength of correlations involved in such a finite-bias conductance anomaly, a proper non-equilibrium treatment will be necessary. As we demonstrate below, the qualitative signature of Kondo correlations is a finite-bias conductance peak which is markedly sharper than the magnitude of the threshold bias.

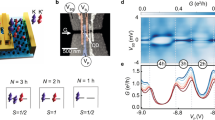
We have examined a quantum dot based on a single-wall carbon nanotube (see Fig. 1a). Electron transport measurements of the two-terminal differential conductance were carried out in a cryostat with a base electron temperature of Tel≈80 mK and a magnetic field perpendicular to the nanotube axis. The low-temperature characteristics of the device are seen from the density plot in Fig. 1b, showing dI/dV as a function of source–drain voltage V and gate voltage Vg. The dominant blue regions of low conductance are caused by Coulomb blockade (CB), whereas the sloping white and red lines are edges of the CB diamonds, where the blockade is overcome by the finite source–drain bias. Moreover, white and red horizontal ridges of high conductance around zero bias are seen. These ridges occur in an alternating manner, for every second electron added to the nanotube dot. These are the Kondo resonances induced by the finite electron spin S=1/2 existing for an odd number N of electrons where an unpaired electron is localized on the tube. The zero-bias resonances are absent for the other regions (with even N) where the ground-state spin is S=0. Over most of the measured gate-voltage range (not all shown), the diamond plot shows a clear four-electron periodicity, consistent with the consecutive filling of two non-degenerate sub-bands, corresponding to the two different sublattices of the rolled-up graphene sheet, within each shell19. This shell-filling scheme is illustrated in Fig. 1c.

Figure 1: Experimental setup and shell-filling scheme for a single-wall carbon nanotube.
figure 1

a, Schematic diagram of the nanotube device, comprising a single-wall carbon nanotube grown by chemical vapour deposition on a SiO2 substrate and contacted by Cr/Au source and drain electrodes, spaced 250 nm apart. Highly doped silicon below the SiO2 cap layer acted as a back-gate electrode. Room-temperature measurements of conductance as a function of back-gate voltage, Vg, indicate that the conducting nanotube is metallic with a small gap outside the region considered here (see Supplementary Information, Section S1). b, Density plot of dI/dV as a function of V and Vg at Tel=81 mK. c, Diagram illustrating the corresponding level filling scheme with N defined as the total number of electrons modulo 4.

Full size image

We observe inelastic cotunnelling features for all even N at e V ∼±Δ for a filled shell and e V ∼±δ for a half-filled shell. Reading off the addition, and excitation energies throughout the quartet near Vg=−4.90 V, shown in Fig. 1b, we can estimate the relevant energy scales within a constant interaction model19,23,24. We deduce a charging energy EC≈3.0 meV, a level spacing Δ≈4.6 meV, a sub-band mismatch δ≈1.5 meV, and rather weak intradot exchange, and intra-orbital Coulomb energies J,dU<0.05δ. The fact that δ>J is consistent with a singlet ground state for a half-filled shell, involving only the lower sub-band (orbital), together with a triplet at excitation energy δ−J and another singlet at energy δ. It should also be noted that the regions with odd N and doublet ground state have an inelastic resonance at an energy close to δ. We ascribe these to (possibly Kondo-enhanced) transitions exciting the valence electron from orbital 1 to orbital 2, but we shall not investigate these resonances in detail. Focusing on the half-filled shell, that is N=2, Fig. 2a shows the measured line shape, dI/dV versus V, at Vg=−4.90 V and for Tel ranging from 81 to 687 mK. The conductance is highly asymmetric in bias voltage and exhibits a pronounced peak near V ∼δ/e which increases markedly when lowering the temperature (see Fig. 2a, inset).

Figure 2: Temperature and magnetic-field dependence of the finite-bias resonance.
figure 2

a, dI/dV as a function of V, at Vg=−4.90 V (dashed cross-section in Fig. 1b), taken at Tel=81 (thick line), 199, 335, 388, 488, 614, 687 (dashed line) mK. Inset: temperature dependence of the finite-bias conductance peak in a (open circles) and the neighbouring zero-bias Kondo resonance (filled circles) at Vg=−4.96 V (see Fig. 1a). The open circles are consistent with the saturation of a log-enhanced finite-bias Kondo peak as T becomes smaller than the spin-relaxation rate Γ≈250 mK, determined from the parameters in Fig. 4. The filled circles follow the numerical renormalization group interpolation formula a(1+(21/0.22−1)(T/TK)2)−0.22 with a=0.11 and TK=1.0 K (dashed line). b, dI/dV versus V and magnetic field B, at Vg=−4.90 V. c, dI/dV versus V at B=6 T, corresponding to vertical cross-section (dashed) in b. The d2I/dV 2 trace (thin line) underlines the presence of three distinct peaks in dI/dV. The black bars each correspond to ΔV =g μBB/e with g=2.0 for nanotubes.

Full size image

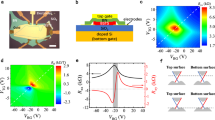
For N=2, we model the nanotube quantum dot by a two-orbital Anderson impurity occupied by two electrons coupled to the leads by means of four different tunnelling amplitudes ti α, between orbitals i=1,2 and leads α=L,R. In terms of the conduction electron density of states, νF, which we assume to be equal for the two leads, the tunnelling induces a level broadening . In the Kondo regime, Γi≪EC, charge fluctuations are strongly suppressed and the Anderson model becomes equivalent to a Kondo model incorporating second-order superexchange (cotunnelling) processes, like that illustrated in Fig. 3a, in an effective exchange–tunnelling interaction (see Supplementary Information, Section S2). This effective model describes the possible transitions between the five lowest-lying two-electron states on the nanotube (see Fig. 3b). As J≪δ, we neglect J and assume that the four excited states are all degenerate with excitation energy δ. The next excited state is a singlet entirely within orbital 2 with excitation energy 2δ (see Supplementary Information, Section S2). Although this state is merely a factor of two higher in energy than the five lowest-lying states, we shall neglect this and all higher-lying states. As there are no spin-flip transitions connecting the ground-state singlet to the excited singlet at energy 2δ, we expect this omission to have a minute influence on the conductance for V <2δ.

Figure 3: Schematic diagram of the inelastic spin-exchange underlying the Kondo effect.
figure 3

a, Illustration of the cotunnelling mechanism giving rise to the effective exchange interaction in the Kondo model. Note that the virtual intermediate state (red spins) in panel 2 is suppressed by a large energy denominator of the order of the electrostatic charging energy of the nanotube. b, Schematic diagram of the five different low-energy states retained in the effective Kondo model: |s〉 is the singlet ground state, |m〉 (m=1, 2, 3) are the triplet components with excitation energy δ−J≈δ and |s′〉 is the corresponding singlet with excitation energy δ. Applying a magnetic field causes the triplet to split up as seen in Fig. 2b,c. c, Renormalized dimensionless exchange–coupling versus incoming conduction electron energy ω, measuring the amplitude for exchange–tunnelling from right to left lead while de-exciting an electron on the nanotube from orbital 2 to 1. The different colours encode the different stages of the RG flow as the bandwidth is reduced from D0 (black) to zero (red). Parameters as in Fig. 4.

Full size image

To deal with the logarithmic singularities arising in low-order perturbation theory (PT) within the Kondo model, it is convenient to use the so-called poor man’s scaling method25. As we have demonstrated earlier26, this method can also be generalized to deal with non-degenerate spin states, such as a spin-1/2 in a magnetic field, as well as with non-equilibrium systems where the local spin degrees of freedom are out of thermal equilibrium with the conduction electrons in the leads. The present problem is complicated by the presence of the two finite energy scales, e V and δ, causing the renormalization of the couplings to involve more than just scattering near the conduction-electron Fermi surfaces. To accommodate for this fact, we must allow for different renormalization at different energy scales, and the poor man’s scaling method should therefore be generalized to produce a renormalization group (RG) flow of frequency-dependent coupling functions. The details of this method are presented in refs 2627 and the specific RG equations for this problem are presented in the Supplementary Information, Section S3.

These coupled nonlinear RG equations do not lend themselves to analytical solution but may be solved numerically with relatively little effort. From this solution, we obtain renormalized coupling functions with logarithmic peaks at certain frequencies determined by e V and δ (see, for example, Fig. 3c). As resonant spin flips only take place through the excited states at energy δ, Korringa-like spin relaxation, through excitation of particle–hole pairs in the leads, partly degrades the coherence required for the Kondo effect28. Therefore, even at zero temperature, the couplings remain weak and increase roughly as , with Γ being the effective (V-dependent) spin-relaxation rate. Using the parameters tα i from the fit in Fig. 4, we calculate the Kondo temperature and the spin-relaxation rate and find that TK≈2 mK and Γ≈250 mK (see Supplementary Information, Sections S3–S5). This in turn implies a small parameter 1/ln(δ/TK)≈0.1, which justifies our perturbative approach. Notice that the smallness of TK corresponds roughly to a mere 30% reduction of the total hybridization to orbital 1 as an electron is added to the nanotube. This tiny TK does not show up directly in the V-dependence of the nonlinear conductance, for example, in the width of the peak, which is characterized instead by the excitation energy δ and the spin-relaxation rate Γ.

Figure 4: Fitting the nonlinear conductance by perturbative RG calculation.
figure 4

a, Experimental data (red circles) at the lowest temperature, fitted by the perturbative RG calculation (white circles) with and T=Tel=81 mK. We use J=0 and an arbitrary bandwidth, D0=1 eV, larger than all other energy scales. From the bias at which dI/dV versus V has maximum slope, we read off δ≈1.5 meV. The blue circles represent simple cotunnelling, that is, second-order PT with tunnelling amplitudes ti α fitted to the data at T=687 mK see (b). b, Comparison with the data (red and white circles) at the highest temperatures, using the same parameters as in a, but with T=Tel=687 mK. The blue curve represents the best fit of second-order PT with T=687 mK.

Full size image

Having determined the renormalized coupling functions, the electrical current is finally calculated from the golden rule expression:

where μL/R=±e V/2 denotes the two different chemical potentials, ħ is Planck’s constant, nγ are the non-equilibrium occupation numbers of the five impurity states and gR,σ′;L,σγ′;γ(ω) is the renormalized exchange–tunnelling amplitude for transferring a conduction electron from left to right lead and changing its spin from σ to σ′, while switching the impurity state from γ to γ′. Figure 4 shows a comparison of this calculation to the data, obtained by fitting the four tunnelling amplitudes ti α determining the unrenormalized exchange couplings. Note that the measured conductance at V =0 and at |V |≫δ, together with the asymmetry between positive and negative bias, places strong constraints on these four amplitudes. The resulting fit is highly satisfactory, with only slight deviations at the highest voltages.

To quantify the importance of Kondo correlations, we also make a comparison with plain non-equilibrium cotunnelling. This unrenormalized second-order tunnelling mechanism clearly underestimates the conductance peak at positive bias, and most severely so at the lowest temperature. Qualitatively, simple non-equilibrium cotunnelling gives rise to a cusp in the conductance which is roughly as wide as the magnitude of the threshold bias itself. As is evident from the data and analysis presented here, non-equilibrium Kondo correlations instead produce a conductance anomaly which is sharper than the magnitude of the threshold—that is a proper finite-bias peak.