Main

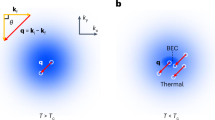
Hanbury Brown and Twiss correlations can be related to a quantum interference effect reflecting the multimode nature of the source2. In analogy to thermal light sources, atom bunching in expanding thermal Bose gases has been observed4,5,6,7,8. Well above the condensation threshold, thermal Bose gases are sufficiently dilute such that atom–atom interactions are negligible and ideal gas theory provides an accurate description.

Extending the atom–photon analogy into the quantum degenerate regime, the absence of bunching has been observed in an out-coupled atom-laser10,11 and in an expanding Bose–Einstein (BE) condensate6,8. This suggested a perfect coherence of these systems, similar to a monomode optical laser where interferences leading to Hanbury Brown and Twiss correlations are essentially absent, yielding only spatially and temporally uncorrelated Poissonian shot noise12.

However, studies of first-order coherence properties of Bose gases near the BE condensation phase transition have revealed the importance of thermal excitations, reducing the coherence also below threshold13,14. Moreover, atom–atom interactions have been identified as a cause for a multimode nature in very elongated degenerate Bose gases. Originally predicted for the limit of weakly interacting degenerate 1D systems15, similar behaviour is also present for very elongated 3D degenerate Bose gases16,17. This effect has been demonstrated experimentally through measurements of density fluctuations18 or two-point correlations19 for temperatures significantly below the BE condensation threshold.

In the following, we probe the second-order correlation function g2 of expanding Bose gases across the BE condensation phase transition, at zero and finite distances, to map out the gradual establishment of matter-wave coherence. Varying the source geometry, we explore the regime from ‘3D’ to ‘quasi-1D’ physics. Close to the BE condensation threshold, the fluctuations of the most populated quantum modes are significant and common theoretical models describing interacting Bose gases, as in refs 15, 16, 17, fail. We therefore restrict our analysis to a qualitative comparison to ideal Bose gas theory predictions, allowing us to cover all investigated regimes.

The function (r,r′) measures the probability of joint detection of two particles at positions r and r′ and hence relates to the density fluctuations of the system and their spatial correlations. For an ideal Bose gas above the BE condensation threshold, (0)=2, highlighting an excess of density fluctuations (bunching). For finite distances, (r,r′) decays to unity on the length scale of the temperature-dependent coherence length. For a true monomode source, (r,r′)=1, demonstrating perfect coherence. In general the shape of (r,r′) reflects the interplay between the occupied modes of the system through the spatial scales of density fluctuations.

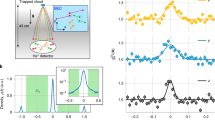
To obtain the second-order correlation function of a Bose gas after its release from the trap, we use our novel fluorescence imaging20. Its high spatial resolution, single-atom sensitivity and exquisite signal-to-noise ratio enables us to probe the function with an accuracy at the per cent level. We record a thin slice of the atomic density in the horizontal x–y plane at the central part of the gas after 46 ms expansion (Fig. 1a,b). The thickness of the slice is set to 225 μm by adjusting the duration of the excitation pulse to 500 μs.

Figure 1: Fluorescence imaging of density correlations.
figure 1

a, Schematic of the experimental geometry. b, Example of the density distribution (lateral cut, log scale) of a Bose gas slightly below the Bose–Einstein condensation threshold after 46 ms expansion time. c, Profile of b, integrated along y. The red line indicates a fit to the density distribution of the thermal fraction, yielding the temperature T.

Full size image

Our matter-wave source is a 87Rb gas of adjustable temperature prepared in the |F,mF〉=|1,−1〉 state in an atom chip magnetic trap21. The chip design allows us to control the parameters of the magnetic trap and hence the shape of the source over a large range of aspect ratios λ=ωy,z/ωx from 4 to 120, where ωx and ωy,z are the axial and radial trap frequencies respectively22.

Modifying the aspect ratio of the trap we explore different regimes of Bose gases (Supplementary Information). For the most isotropic traps (λ=4.75,13.5), gases significantly below the BE condensation threshold can be considered in the Thomas–Fermi regime with a chemical potential μ of the order of 3 to 4 ℏωy,z. In this case the expansion starts with a hydrodynamic phase. For the most elongated trap (λ=113), gases with temperatures below the degeneracy threshold have μ slightly smaller than ℏωy,z, entering the weakly interacting quasi-1D regime23. In this case the expansion of the system is essentially collisionless17.

We obtain the temperature of the system T and deduce the number of atoms in the thermal fraction of the gas Nth by fitting the thermal tails of the axial (x axis) density profiles using an analytical formula based on ideal Bose gas theory (Fig. 1c). By comparing the fit result to the total observed signal, this also yields the number of condensed atoms (if present) within the measured slice. A simple model for the expansion of the degenerate fraction of the gas yields NBEC, the total number of condensed atoms. Finally, for each set of temperature T and total atom number N=Nth+NBEC, we estimate the critical temperature of the system through the relation , where Tc(N) corresponds to ideal Bose gas theory predictions for the critical temperature. The experimentally obtained factor α depends exclusively on the source aspect ratio λ (see Methods).

Averaging over typically one hundred experimental repetitions with identical experimental parameters, we calculate the mean autocorrelation of the density slices and normalize it by the autocorrelation of the mean density slice. We obtain the normalized density correlation function n2, which can be decomposed into the sum of two terms, s and g2. The term g2 contains the desired information about two-particle correlations whereas s is a contribution due to atomic shot noise (see Methods).

Typical results of density correlation functions of expanding Bose gases from a moderately anisotropic source (λ=13.5) are shown in Fig. 2. The corresponding graphs for a nearly isotropic trap (λ=4.75) and a quasi-1D gas (λ=113) can be found in the Supplementary Information Figs S1 and S2). The atomic shot noise s appears as a dark oval spot at the centre. Its eigen-axes are rotated by 45° with respect to the axes of the atomic source x,y, corresponding to the direction of the imaging laser beams. The structure corresponding to g2 is visible behind this central spot. Its anisotropy reflects the aspect ratio of the source gas.

Figure 2: Density correlation results.
figure 2

a–c, Density correlation functions of expanding Bose gases n2 (lateral cut in (Δx,Δy) plane) at , , and , respectively. The aspect ratio λ of the atomic source is 13.5. d–f, Circles: radial cuts of a–c. Dashed line: radial cuts of the corresponding autocorrelation of the mean density profile. Solid line: radial cuts of predictions of ideal Bose gas theory for the second-order correlation function g2(0,Δy). g–i, Circles: radially averaged axial cuts of a–c over 160 μmwhere the shot noise peak s is excluded. The width of the exclusion region is 32 μ m. Dashed line: radially averaged axial cuts of the corresponding autocorrelation of the mean density profile. Solid line: radially averaged axial cuts of the predictions of ideal Bose gas theory for the second-order correlation function .

Full size image

For a thermal gas above the BE condensation threshold () we observe bunching. In this region, where inter-particle interactions are weak, we find an almost perfect agreement between the experimental observations and the second-order correlation function g2 simulated within ideal Bose gas theory. As input parameters we take the thermodynamical properties obtained from the data used to compute n2 and account for the imaging resolution9.

Below the critical temperature () the main experimental observations valid for all explored aspect ratios (Fig. 2 and Supplementary Figs S1 and S2) are:

(1) The establishment of coherence along the radial direction. The RMS width of the g2 peak along the y axis grows rapidly when crossing the critical temperature until it saturates owing to the finite radial size of the system (Fig. 2d–f). This can be seen as an experimental observation of the establishment of radial coherence14, where the shape of n2 changes from a decreasing exponential (Fig. 2d–e) to a profile set by the spatial shape of the condensed cloud after expansion (Fig. 2f). The RMS width of the g2 peak is related to the radial coherence length in the trapped system through the hydrodynamic expansion of the gas, which imposes a scaling factor on the radial size of the cloud (see Methods).

(2) g2(0)>1 and the appearance of a dip below unity at finite distances along the axial g2. Owing to the anisotropy of the trap, thermal excitations of the system will typically be spread over more modes axially (x axis) than radially. Below, but close to the BE condensation threshold, few of the lowest lying axial modes will be macroscopically occupied and the shape of the second-order correlation function g2(Δx>0) can then be interpreted as a result of the interference of all contributing modes. Hence the time-of-flight expansion implements a very sensitive heterodyne detection of weakly occupied modes of the matter-wave source. The dip below unity at finite distance Δx along the g2 axial profiles is a direct consequence of this interference (Fig. 2h,i). This observation is similar to observations reported in recent experiments and theoretical work on weakly interacting quasi-1D Bose gases17,19 (for a comparison see Fig. 3d–f). Most interestingly we find this behaviour —generally associated with quasi-1D physics—also for the most isotropic trap probed (aspect ratio λ=4.75).

Figure 3: Density correlation comparison.
figure 3

a–c, Peak height of the second-order correlation function of expanding Bose gases for various ratios and three different trap aspect ratios λ=4.75 (light blue), 13.5 (orange) and 113 (green). It is defined as (see the caption of Fig. 2). The solid lines indicate the predictions obtained from ideal Bose gas theory. The light grey areas represent the range where the source is fully thermal. Note that the total atom number N is not held constant between the data points, however this is taken into account in the value of . d–f, Circles: radially averaged axial cuts of the density correlation function n2 (see Fig. 2 caption) with parameters corresponding to the coloured square labelled respectively in a–c. Dashed line: radially averaged axial cuts of the corresponding autocorrelation of the mean density profile. Solid line: radially averaged axial cuts of the predictions of ideal Bose gas theory for the second-order correlation function .

Full size image

We would like to point out that (2) corrects the widely established image of a perfectly ‘flat’ correlation function for a Bose gas immediately below the BE condensation threshold6,8,10,11. Such behaviour highlights the influence of the non-ground-state modes (thermal depletion) of the system, whose population saturates below the BE condensation threshold. Working with small atom numbers and our highly sensitive detector allow us to accurately probe the transition regime and the graduate saturation of excitations when crossing the BE condensation threshold.

To give an overview we show the behaviour of , set by g2(0), for all three measured aspect ratios and temperatures in a wide range of different ratios in Fig. 3a–c. Most strikingly we find g2(0)>1 for all temperatures and aspect ratios, which indicates a persistent multimode nature even for a 3D BE condensate far below the condensation threshold. Lowering the temperature we observe a slow decrease of the amplitude of Hanbury Brown and Twiss correlations, which illustrates the gradual reduction of the thermal depletion of the system.

Ideal Bose gas theory reproduces the basic physics and the qualitative features of the experimental observation for moderate aspect ratios as discussed above also below the critical temperature. We attribute the remaining quantitative deviations between this description and our observations to particle interactions (Fig. 3d–f and Supplementary Figs S1 and S2).

For highly anisotropic sources with a large aspect ratio (λ=113) close to a quasi-1D system (μ<ℏω), we observe no reduction of g2(0) with temperature (Fig. 3c and Supplementary Fig. S2). This behaviour is expected for very elongated systems, where low lying axial excitations of the system remain macroscopically occupied also significantly below the degeneracy temperature15,16,17,19. It is based on the dominant influence of particle interactions, hence ideal Bose gas theory fails to describe even the qualitative behaviour at .

Our experimental findings call for a more complete theoretical description of interacting Bose gases at the threshold to Bose–Einstein condensation, where fluctuations of competing modes are significant. With such a theory at hand, measurements of density correlations will allow a detailed quantitative characterization of the mode occupation of the source. For equilibrium systems well below the BE condensation threshold this can be used for precision thermometry, where methods based on the observation of a thermal background fail (as demonstrated for deeply degenerate 1D systems17,19). For ultralow temperatures well below the chemical potential this would allow one to probe quantum fluctuations, for example quantum depletion, of 3D or 1D Bose gases. Our studies can directly be extended to non-equilibrium systems, where fundamental questions on equilibration, thermalization and integrability arise24,25,26.

Methods

Experimental set-up.

We prepare ultracold gases of a few 104 87Rb atoms in the |F,mF〉=|1,−1〉 state confined in one out of three different Ioffe–Pritchard type magnetic traps obtained using a multilayer atom chip22. The parameters of the three harmonic traps are respectively ωx=2π×20 Hz axially and ωy,z=2π×2 260 Hz radially (λ=113), ωx=2π×160 Hz axially and ωy,z=2π×2 180 Hz radially (λ=13.5) and ωx=2π×320 Hz axially and ωy,z=2π×1 520 Hz (λ=4.75) radially.

We use forced radio-frequency (RF) evaporation to cool the gas close to or below the Bose–Einstein condensation threshold. As a direct consequence, colder gases contain less atoms and their corresponding critical temperature decreases as well. Here , where N is the total number of atoms, , ℏ and kB are Planck and Bolzmann constants respectively and ζ(x) is the Riemann zeta function. To ensure thermal equilibrium of the gas we keep a constant RF knife for 200 ms at the end of the evaporative cooling ramp.

Comparison with ideal Bose gas theory.

The constant α introduced in the main text is adjusted such that cooling the gas to coincides with the experimental observation of the appearance of a degenerate fraction of atoms (NBEC≥0). The value of α is slightly smaller than unity for the moderate trap aspect ratios (λ=4.75,13.5), which qualitatively agrees with theoretical studies of the shift of the critical temperature of interacting Bose gases27. For the most elongated trap (λ=113), α is of the order of three, which qualitatively agrees with predictions for the degeneracy temperature for 1D systems28.

Fit of the axial profile of the thermal fraction.

Using an analytic expression for the density flux I of a freely expanding ideal Bose gas9 and assuming an elliptical Gaussian shape for the excitation beams, hence neglecting any saturation effect, we deduce a formula describing the axial profile of density ‘slices’ of the thermal fraction of expanding Bose gases

that we can use to fit our experimental results. Here t0 is the expansion time, z0 the position of the centre of the excitation laser beam profiles, 2Δt the exposure time and w the RMS width of the excitation beams. For the data presented in this work t0=46 ms, 2Δt=500 μs and w=10 μm (ref. 20). This model depends on two parameters, the temperature of the gas T and its fugacity, which fixes the total number of atoms in the thermal fraction of the gas Nth. To avoid the divergence of the population of the ground state of the system when the fugacity reaches its maximum, only the excited states of the ideal Bose gas are considered for the calculation of ρls(x).

Estimation of NBEC.

For traps with moderate aspect ratios (λ=4.75,13.5), the condition μ≫ℏωx,y,z is fulfilled quickly after passing the BE condensation threshold (Supplementary Fig. S3) and the condensed part of the system can then be assumed to be in the Thomas–Fermi regime. Scaling laws can then be used to describe the gas expansion29,30. We find scaling factors of 6 (axial) and 625 (radial) for λ=13.5 and 28 (axial) and 430 (radial) for λ=4.75 respectively. With such a model, deducing the number of condensed atoms NBEC from the number of condensed atoms counted in a density slice is straightforward.

For the most anisotropic trap (λ=113), we use an isotropic Gaussian ansatz for the radial density distribution of the degenerate fraction of the gas. Fitting the RMS width of the Gaussian along the y axis, it is then straightforward to infer NBEC.

Density correlation function.

The density correlation function is the sum of the two contributions g2 and s. The first term g2 can be expressed as , where is an average of the second-order correlation function g2(r,r′) over the spatially inhomogeneous density profile of the gas with Δr=r−r′ kept fixed, o2 is the effective two-particle point spread function of the fluorescence imaging and * is the convolution product. The function o2 accounts for the diffusion of single atoms during the imaging process and optical aberrations, which blur the position of single atoms in the images20. The other contribution to the density correlation function s is due to the atomic shot noise and is proportional to the inverse of the mean density of the gas.

Here we slightly extend the analytic expression of the second-order correlation function of an expanding ideal Bose gas derived in ref. 9 to take into account the imaging scheme. Using a 2D isotropic Gaussian model for o2, we obtain an analytic expression for g2.