Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas

Abstract

Magnetic reconnection releases energy explosively as field lines break and reconnect in plasmas ranging from the Earth’s magnetosphere to solar eruptions and astrophysical applications. Collisionless kinetic simulations have shown that this process involves both ion and electron kinetic-scale features, with electron current layers forming nonlinearly during the onset phase and playing an important role in enabling field lines to break^1,2,3,4. In larger two-dimensional studies, these electron current layers become highly extended, which can trigger the formation of secondary magnetic islands^5,6,7,8,9,10, but the influence of realistic three-dimensional dynamics remains poorly understood. Here we show that, for the most common type of reconnection layer with a finite guide field, the three-dimensional evolution is dominated by the formation and interaction of helical magnetic structures known as flux ropes. In contrast to previous theories¹¹, the majority of flux ropes are produced by secondary instabilities within the electron layers. New flux ropes spontaneously appear within these layers, leading to a turbulent evolution where electron physics plays a central role.

Main

Thin current layers are the preferred locations for magnetic reconnection to develop. The most common configuration in nature is guide-field geometry, where the rotation of magnetic field across the layer is less than 180°. Present theoretical ideas of how reconnection proceeds in these configurations are deeply rooted in early analytical work¹¹ that, if correct, would imply a direct transition to three-dimensional (3D) turbulence due to a broad spectrum of interacting tearing instabilities. At the core of this idea is the notion that a spectrum of tearing instabilities develops across the initial current sheet for perturbations satisfying the local resonance condition. As these modes grow, the resulting magnetic islands would overlap, leading to stochastic magnetic-field lines and a turbulent evolution. Recently, this type of scenario was proposed as a mechanism for accelerating energetic particles during reconnection¹². Similar ideas for generating turbulence have been studied in fusion plasmas¹³ using resistive magnetohydrodynamics (MHD) and two-fluid¹⁴ models. Alternatively, other researchers have imposed turbulent fluctuations within MHD models in an attempt to understand the consequences¹⁵. In either case, these results are not applicable to the highly collisionless environment of the magnetosphere, where reconnection is initiated within kinetic ion-scale current layers. The ability to study the self-consistent generation of turbulence during magnetic reconnection with first-principles 3D simulations has only become feasible in the past year.

The 3D simulations were carried out on two petascale supercomputers, Roadrunner and Kraken, using the kinetic particle-in-cell code VPIC (refs 16, 17), which solves the relativistic Vlasov–Maxwell system of equations. These capabilities have permitted a series of simulations using over 10¹² computational particles, nearly 10³ larger than previous two-dimensional (2D) studies⁵. The case described here is initialized with a Harris¹⁸ current sheet, with magnetic field B=B_x0tanh(z/λ)e_x+B_y0e_y where e_x and e_y are unit vectors, λ=d_i is the initial half-thickness, d_i is an ion inertial length, B_y0=B_x0 is a uniform guide field, the ion to electron mass ratio is m_i/m_e=100 and further details regarding the set-up are given in the Methods section.

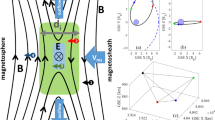
The simulation results in Fig. 1 reveal some dramatic differences from the basic ideas discussed above. First, the concept of magnetic islands in real 3D systems corresponds to extended flux ropes, which can interact in a variety of complex ways not possible in 2D models. Examples of such complexity were reported in recent experiments involving small flux ropes produced with plasma guns^19,20. In contrast, the flux ropes shown in Fig. 1 are generated by the tearing instability over a range of oblique angles θ<19°, which is substantially less than the expected θ<40° for these parameters^11,21. Indeed, these results demonstrate a few dominant modes that are localized near the centre of the initial layer. The orientation of these ropes can be directly measured by examining B_z near the symmetry plane (z=0) as shown in Fig. 1b, or by computing the power spectrum of B_z over the simulation domain as shown in Fig. 1c. The dominant modes correspond to k_xd_e≈0.08 with θ≡tan⁻¹(k_y/k_x)≈±14°, where d_e is the electron skin depth. Some of the interesting 3D features in Fig. 1 arise from the interaction of these flux ropes, leading to a complex connectivity of magnetic-field lines. However, the observed dynamics at this time is much simpler than expected from previous theories.

Figure 1: Formation of primary flux ropes.

a, At early time tΩ_ci=40, the tearing instability gives rise to flux ropes as illustrated by an isosurface of the particle density coloured by the magnitude of the current density (normalized by J₀≡c B_x0/(4π λ)) along with sample magnetic-field lines (yellow). b, Typical angles θ≡tan⁻¹(k_y/k_x) for these ropes are directly measured by examining B_z at the centre of the layer (z=0). c, The power spectrum of is shown on a log scale. The solid white line corresponds to the dominant angle in the spectrum.

Here we reconsider the linear kinetic theory and demonstrate not only that the traditional asymptotic approaches fail dramatically for the oblique tearing modes, but also that realistic predictions can be obtained with numerical techniques. We consider a general electromagnetic perturbation with wavevector k=k_xe_x+k_ye_y that satisfies the resonance condition k · B=0 at a location z_s=−λtanh⁻¹[k_yB_y0/(k_xB_x0)]. The standard approach involves an asymptotic matching between an outer MHD region with a kinetic description within the resonance layer^22,23. The solution for the outer region features a discontinuity in the first derivative of the perturbed magnetic field across the resonance layer, which captures the destabilizing influence of magnetic shear that drives tearing. However, previous theories¹¹ used an incorrect equation for the outer region, which does not recover MHD (ref. 24) for the oblique modes. Correcting for this error, we obtain

where k≡|k| and is the perturbed magnetic field. The term in brackets causes Δ′ to increase for modes localized on the edge of the layer tanh[z_s/λ]=tan(θ)B_y0/B_x0, corresponding to oblique angle θ≡tan⁻¹(k_y/k_x). Using this solution for Δ′ and neglecting the electrostatic perturbation within the resonance layer results in growth rate and real frequency

where ρ_i=$v_{t{h}_{\text{i}}}$/Ω_ci, $v_{t{h}_{\text{i}}}$=(2T_i/m_i)^1/2, Ω_ci≡e B_x0/(m_ic), U_e=2c T_e/(e B_x0λ) is the electron drift velocity, α≡[T_em_e/(T_im_i)]^1/2 and the angular dependence of the growth rate is

For weak background density , equation (1) implies that the fastest-growing modes are oblique for B_y0/B_x0>((1−k λ)/(1−k λ/2))^1/2. Even before this condition is reached, modes are destabilized for Δ′>0, corresponding to angles up to θ_max=tan⁻¹(B_x0/B_y0).

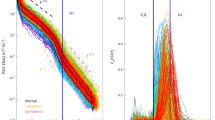
Even with the corrected Δ′, these results are in clear disagreement with Fig. 1, because the predicted range of angles θ_max=±45° is much broader than actually observed. However, the asymptotic theory is based on the ordering λ≫ρ_i, whereas our focus is ion-scale layers λ∼ρ_i, where the onset of reconnection is thought to occur in magnetospheric plasmas. To treat this regime rigorously, we employ an exact numerical approach which solves the linearized Vlasov–Maxwell system^25,26. As shown in Fig. 2, these exact growth rates are in good agreement with equation (1) for the limit of an electron–positron plasma m_i=m_e at all angles. At high mass ratio, equation (1) also works reasonably well for modes with k_y=0, and the agreement improves for thicker current sheets where the asymptotic theory is better justified. However, the asymptotic theory fails dramatically at oblique angles, even for the thicker layers. The exact Vlasov results predict that the unstable modes are limited to θ_max<20° for m_i/m_e=100, in good agreement with the simulation results in Fig. 1. Since the range of unstable modes θ_max<15° in a hydrogen plasma is quite similar, these results provide a nice justification for the reduced mass ratio employed in this letter. The real frequency in Fig. 2d is also a bit lower than expected from equation (1), but the dramatic failure of the asymptotic theory is not well understood. We note that the eigenfunction obtained for oblique modes with m_i/m_e≫1 is complex, with a rapid change in phase across the ion resonance layer, a feature that is inconsistent with the asymptotic matching.

Figure 2: Theoretical predictions for oblique tearing instability.

The asymptotic theory (solid) from equation (1) is compared with the exact Vlasov results²⁵ (dashed) as a function of oblique angle θ=tan⁻¹(k_y/k_x) for the mass ratio m_i/m_e and sheet thickness λ indicated. a–c, The growth rate; d, the real frequency corresponding to c. Other parameters are held fixed, k λ=0.4, B_y0=B_x0, T_i=T_e and n_b=0.3n₀.

For parameter regimes relevant to magnetospheric plasmas, these results demonstrate that the spectrum of oblique tearing modes is much narrower than previous expectations, which implies that the generation of turbulence by overlapping magnetic islands cannot proceed as previously thought. Although the narrow spectrum of modes persists even for thicker current sheets λ=5ρ_i, it remains unclear if this holds for λ≫ρ_i or stronger guide fields B_y0≫B_x0. However, over longer timescales these simulations reveal a new scenario in which flux ropes can be generated through secondary instabilities in the highly extended electron-scale current sheets that form nonlinearly during the onset of reconnection. These electron layers are a general feature of fast reconnection in collisionless plasmas and play a crucial role in breaking the frozen-in condition^1,2,3,4. In sufficiently large systems, previous 2D simulations have demonstrated that these layers may become highly extended and form secondary magnetic islands^5,6,7,8,9,10. However, the manner in which this can occur is vastly expanded in three dimensions. To illustrate this point, Fig. 3 compares a slice of the current density between the 3D and a corresponding 2D case at time tΩ_ci=78. Whereas the current layers along the separatrices are stable in two dimensions, these layers are violently unstable in three dimensions to the formation of flux ropes over a wide range of oblique angles as shown in Fig. 3a, causing the current density to become highly filamented and time dependent.

Figure 3: Formation of secondary flux ropes.

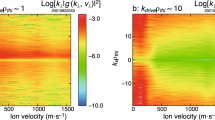
a,b, Slice of the current density at y=35d_i from the 3D simulation (a) compared with the corresponding 2D result (b). c, The structure of the separatix layer at the location indicated. Profiles in c are shown in the minimum-variance frame (18° rotation about y followed by 52° rotation about z′). d, Fitting to a Harris profile gives a half-thickness λ≈2d_e with guide field B_y′≈4.4B_x0′, resulting in the growth rate shown. e, The power spectrum for the 3D simulation on a log scale. The solid white line corresponds to the dominant angle, whereas the dashed line is the simple estimate from c.

It seems that these dramatic differences between two and three dimensions are due to tearing-type instabilities driven by the strong magnetic shear across the electron-scale layers. To demonstrate this mechanism, the profiles of the current density and magnetic field are shown in Fig. 3c across the separatrix layer in the 2D simulation. Fitting the profiles to a local Harris sheet corresponds to λ≈2d_e, with a magnetic shear angle of 26° across the layer. The kinetic theory²⁶ for these parameters in Fig. 3d predicts γ/Ω_ci≈0.42 for the fastest-growing modes with k d_e≈0.2. At realistic hydrogen mass ratio, the growth rate increases to γ/Ω_ci≈4.2 assuming that the layer thickness remains on the scale ∼2d_e. The separatrix current layer in Fig. 3b from the left boundary to the first X line is approximately ∼220d_e long, which implies it should break up into seven filaments, whereas there are four rope structures visible in Fig. 3a. However, this separatrix layer actually begins to break up at time tΩ_ci≈60, and originally forms six filaments. Thus some of these structures have already coalesced by time tΩ_ci≈78 shown in Fig. 3. The angle of the modes is determined by k · B=0 near the centre of the electron layer at the time of break-up. The sample profiles from the 2D case in Fig. 3b,c correspond to θ≈52°, which is larger than the observed angles for these structures in Fig. 3a. Again, exact agreement is not expected because filamentary structures begin forming at earlier time in the 3D simulation. To better quantify the structure of the magnetic-field perturbations, the power spectrum of B_z is given in Fig. 3e. The form of the spectrum is much broader in k space and indicates the presence of highly anisotropic narrow structures in B_z, which are signatures of the flux ropes. The peak power occurs for θ≈±34°, but there is actually significant power out to θ≈52° consistent with the above estimate. On the basis of these results, it seems that the growth time, wavelength and angle of these structures are consistent with tearing instabilities in the electron layers.

The 3D structure of the turbulent reconnection is illustrated in Fig. 4 at somewhat later time tΩ_ci=98, where the oblique flux ropes have grown to larger amplitude and the helical magnetic-field structure of the ropes is clearly visible. The simulation is dominated by the interaction of highly anisotropic structures across multiple scales, including electron-scale current sheets that continually reform and break up into filaments, along with flux ropes generated at these scales and quickly growing well above ion scales. This turbulence is highly inhomogeneous and is continually self-generated within the reconnection layer, which in the present study is embedded in an otherwise laminar plasma.

Figure 4: Development of turbulent reconnection.

At late time tΩ_ci=98, the secondary flux ropes have grown to large amplitudes and interact over a wide range of angles, giving rise to a turbulent evolution. The 3D structure is illustrated by an isosurface of particle density coloured by current density, along with selected magnetic-field lines (yellow). To illustrate the observational signatures of these flux ropes, the normal magnetic field B_z, total magnetic field |B| and electron density n_e are plotted along two trajectories.

These results have immediate implications for spacecraft observations of magnetic reconnection. In the solar wind, observational studies of reconnection²⁷ are based on an assumed, idealized, 2D geometry with flux ropes centred in the reconnection exhaust. Neither of these assumptions is consistent with the structure observed in Fig. 4. Our results indicate the need to expand the identification criteria to cover the more complex behaviour reported here. Indeed, whereas many examples of essentially 2D laminar exhausts have been reported²⁷, other cases indicate that more complicated features are present²⁸. However, essentially all observations of reconnection in the solar wind are >1,000d_i downstream from an active X line, and it remains unclear from our initial study how far downstream this turbulence might persist in these extremely large systems.

At the magnetopause, flux ropes are commonly referred to as flux transfer events²⁹ and may play an important role in transport across the magnetopause. However, their formation mechanism and precise signatures remain under debate. Of the leading ideas^29,30,31, these simulations are more consistent with the multiple-X-line model³⁰ rather than the single-X-line model³¹, but with important differences. Observationally, the degree of asymmetry in the bipolar magnetic field B_z is an important signature for identifying flux transfer events and distinguishing between models. For example, the nearly symmetric bipolar B_z signature in the bottom right panel of Fig. 4 is generally consistent with the multiple-X-line model^32,33. However, a different trajectory through these same structures (left panel) shows strong asymmetries in the bipolar B_z, which researchers might interpret in terms of the single-X-line model^32,33. Clearly, the actual 3D structure in Fig. 4 is more complicated than the simple models currently employed, which implies that many flux ropes may not have been properly recognized in previous studies. These results are important for the upcoming Magnetospheric Multiscale Mission, which is focused on the role of electron physics in collisionless reconnection. The high-time-resolution diagnostics on this mission will enable measurements of the extended electron layers as they break up into flux ropes near reconnection sites.

Methods

The simulation is initialized with a Harris¹⁸ current sheet and, to better mimic a large open system, open boundary conditions⁵ are employed in the x and z directions with periodic boundary conditions in the y direction. Following previous 2D studies⁵, a weak 4% magnetic perturbation is included to set up a large-scale flow pattern consistent with the open boundaries, while still enabling linear modes to grow. The initial density profile is n(z)=n₀sech²(z/λ)+n_b, where n₀ is the central Harris density and n_b is a uniform background density. Lengths are normalized by the ion d_i=c/ω_pi and electron d_e=c/ω_pe inertial scales, where ω_ps=(4π e²n₀/m_s)^1/2 for each species s=i,e. The domain size is L_x×L_y×L_z=70d_i×70d_i×35d_i with 2,048×2,048×1,024 cells. The simulation used 120 particles per cell for each species, corresponding to a total of ∼10¹² particles. Other parameters are λ=d_i, m_i/m_e=100, B_y0=B_x0, T_i=T_e and ω_pe/Ω_ce=2 where Ω_ce=e B_x0/(m_ec). To ensure that magnetic flux enters the system in a controlled fashion, the open boundary conditions were modified on the z boundaries to uniformly drive a prescribed inflow U_z=0.08V_A[1−exp(−t/τ)] where is the Alfvén velocity and τΩ_ci=80. The spectra in Figs 1 and 3 were computed with a discrete Fourier transform of B_z in all three spatial directions. In both the z and x directions a Blackman window³⁴ was employed to suppress spurious features in the spectrum from the non-periodic boundary conditions. Finally, the reduced spectrum corresponds to a sum over k_z.