Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Quantum random networks

Nature Physics volume 6, pages 539–543 (2010)Cite this article

Abstract

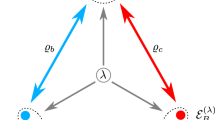
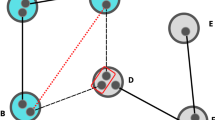
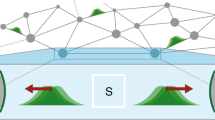
Quantum mechanics offers new possibilities to process and transmit information. In recent years, algorithms and cryptographic protocols exploiting the superposition principle and the existence of entangled states have been designed. They should allow us to realize communication and computational tasks that outperform any classical strategy. Here we show that quantum mechanics also provides fresh perspectives in the field of random networks. Already the simplest model of a classical random graph changes markedly when extended to the quantum case, where we obtain a distinct behaviour of the critical probabilities at which different subgraphs appear. In particular, in a network of N nodes, any quantum subgraph can be generated by local operations and classical communication if the entanglement between pairs of nodes scales as N−2. This result also opens up new vistas in the domain of quantum networks and their applications.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Classical random graphs.
Figure 2: Quantum random graphs.
Figure 3: Graphical representation of |Kc〉.
Figure 4: Construction of quantum subgraphs.
Figure 5: Entanglement generation between two nodes.

Similar content being viewed by others

References

  1. Kimble, H. J. The quantum Internet. Nature 453, 1023–1030 (2008).

    Article  ADS  Google Scholar 

  2. Gisin, N. & Thew, R. Quantum communication. Nature Photon. 1, 165–171 (2007).

    Article  ADS  Google Scholar 

  3. Bennett, C. H. & Brassard, G. in Proc. IEEE Int. Conf. on Computers, Systems and Signal Processing 175–179 (IEEE, 1984).

    Google Scholar 

  4. Perseguers, S. Entanglement Distribution in Quantum Networks. PhD thesis, Technische Univ. München (2010).

  5. Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).

    Article  ADS  MathSciNet  Google Scholar 

  6. Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991).

    Article  ADS  MathSciNet  Google Scholar 

  7. Bennett, C. H. & Wiesner, S. J. Communication via one- and two-particle operators on Einstein–Podolsky–Rosen states. Phys. Rev. Lett. 69, 2881–2884 (1992).

    Article  ADS  MathSciNet  Google Scholar 

  8. Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829–1834 (1999).

    Article  ADS  MathSciNet  Google Scholar 

  9. Acín, A., Cirac, J. I. & Lewenstein, M. Entanglement percolation in quantum networks. Nature Phys. 3, 256–259 (2007).

    Article  ADS  Google Scholar 

  10. Perseguers, S., Cirac, J. I., Acín, A., Lewenstein, M. & Wehr, J. Entanglement distribution in pure-state quantum networks. Phys. Rev. A 77, 022308 (2008).

    Article  ADS  Google Scholar 

  11. Erdős, P. & Rényi, A. On random graphs. Publ. Math. Debrecen 6, 290–297 (1959).

    MathSciNet  MATH  Google Scholar 

  12. Erdős, P. & Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 5, 17–61 (1960).

    MathSciNet  MATH  Google Scholar 

  13. Erdős, P. & Rényi, A. On the evolution of random graphs. II. Bull. Inst. Int. Stat. 38, 343–347 (1961).

    MATH  Google Scholar 

  14. Kochen, M. The Small World (Ablex, 1989).

    Google Scholar 

  15. Watts, D. J. & Strogatz, S. H. Collective dynamics of small-world networks. Nature 393, 440–442 (1998).

    Article  ADS  Google Scholar 

  16. Barabási, A-L. & Albert, R. Emergence of scaling in random networks. Science 286, 509–512 (1999).

    Article  ADS  MathSciNet  Google Scholar 

  17. Bollobás, B. Random Graphs (Academic, 1985).

    MATH  Google Scholar 

  18. Werner, R. F. Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model. Phys. Rev. A 40, 4277–4281 (1989).

    Article  ADS  Google Scholar 

  19. Nielsen, M. A. Conditions for a class of entanglement transformations. Phys. Rev. Lett. 83, 436–439 (1999).

    Article  ADS  Google Scholar 

  20. Vidal, G. Entanglement of pure states for a single copy. Phys. Rev. Lett. 83, 1046–1049 (1999).

    Article  ADS  Google Scholar 

  21. Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).

    Article  ADS  Google Scholar 

  22. Hastings, M. B. Superadditivity of communication capacity using entangled inputs. Nature Phys. 5, 255–257 (2009).

    Article  ADS  Google Scholar 

  23. Greenberger, D. M., Horne, M. A. & Zeilinger, A. Bell’s Theorem, Quantum Theory, and Conceptions of the Universe (Kluwer Academics, 1989).

    Google Scholar 

  24. Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).

    MATH  Google Scholar 

  25. Bollobás, B. Degree sequences of random graphs. Discrete Math. 33, 1–19 (1981).

    Article  MathSciNet  Google Scholar 

  26. Kraus, B. & Cirac, J. I. Discrete entanglement with squeezed light. Phys. Rev. Lett. 92, 013602 (2004).

    Article  ADS  Google Scholar 

  27. Bornholdt, S. & Schuster, H. G. Handbook of Graphs and Networks: From the Genome to the Internet (Wiley-VCH, 2003).

    MATH  Google Scholar 

  28. Watts, D. J. Small Worlds: The Dynamics of Networks Between Order and Randomness (Princeton Univ. Press, 2004).

    MATH  Google Scholar 

  29. Newman, M., Barabási, A-L. & Watts, D. J. The Structure and Dynamics of Networks (Princeton Univ. Press, 2006).

    MATH  Google Scholar 

  30. Albert, R. & Barabási, A-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002).

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We acknowledge support from the EU projects ‘AQUTE’ and ‘QAP’, the ERC grant ‘PERCENT’ and ‘QUAGATUA’, the DPG excellence cluster ‘Munich Center for Advanced Photonics’ and FOR 635, the Spanish MEC Consolider QOIT and FIS2007-60182 and FIS2008-00784 projects, la Generalitat de Catalunya and Caixa Manresa, the Alexander von Humboldt Foundation and the QCCC programme of the Elite Network of Bavaria.

Author information

Authors and Affiliations

  1. Max-Planck–Institut für Quantenoptik, Hans-Kopfermann-Strasse 1, 85748 Garching, Germany

    S. Perseguers & J. I. Cirac

  2. ICFO—Institut de Ciències Fotòniques, Mediterranean Technology Park, 08860 Castelldefels, Spain

    M. Lewenstein & A. Acín

  3. ICREA—Institució Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spain

    M. Lewenstein & A. Acín

Authors
  1. S. Perseguers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Lewenstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. A. Acín
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. J. I. Cirac
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors have equally contributed to this work.

Corresponding author

Correspondence to J. I. Cirac.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Perseguers, S., Lewenstein, M., Acín, A. et al. Quantum random networks. Nature Phys 6, 539–543 (2010). https://doi.org/10.1038/nphys1665

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nphys1665

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing